基于高阶双渐近透射边界的大坝－库水动力相互作用直接耦合分析模型

高毅超，徐艳杰，金 峰，王 翔

1 清华大学水沙科学与水利水电工程国家重点实验室，北京 100084

2 华侨大学土木工程学院，厦门 361021

3 长江勘测规划设计研究有限责任公司，武汉 430010

1 引 言

随着我国水电开发建设的快速发展，大坝工程的规模越来越大.西部地区许多高坝坝高达300米级，水库向上游延伸几十甚至几百公里.如此巨型的水利水电工程，在遭遇强烈地震时，大坝结构、河谷地基、水库库水以及库底的淤砂层之间都会发生显著的动力相互作用，由此给大坝的地震响应带来巨大影响，多年来许多学者在该领域开展了广泛研究［1－6］.其中，如何准确合理地确定坝面动水压力一直是这个领域的研究热点和难点.早在20世纪30年代，Westergaard［7］基于刚性直立坝面和库水不可压缩假设，提出了附加质量法，该方法简单易用，至今仍被工程界广泛接受和应用.然而，坝面动水压力问题十分复杂，大量的研究表明，库水的可压缩性、大坝结构特性、淤砂层特性、地基特性以及坝体、地基、库水和淤砂层之间的动力相互作用等因素都会对坝面动水压力产生影响［8］.对于大坝－库水这个耦合系统，其动力分析必须考虑动水压力波在半无限库水中传播引起的辐射阻尼影响.有限单元法［9－11］、有限差分法［12－14］是模拟波动传播的常用数值方法，但是需要在计算域的截断边界上施加人工边界［15－19］.Zienkiewicz等［20］以 及 Küçükarslan 等［21］采 用Sommerfeld辐射边界提出了结构－流体动力相互作用的数值分析方法.由于Sommerfeld辐射边界只能吸收垂直入射波，在理论上只有零阶精度，需要将其置于远离近场结构的地方以获得较好的精度.边界元法［22－23］能够自动满足无穷远处的辐射边界条件，并且使问题维数降低一维，是模拟动水压力的有效方法.然而在实际应用中，求解边界元法所需的基本解可能十分复杂或者不存在，这大大限制了边界元法在实际工程中的应用.

比例边界有限单元法（Scaled boundary finite element method，SBFEM）［24］是一种半解析的数值方法，它兼具有限单元法和边界元法的优点.该方法只需离散边界而在径向保持解析，使问题维数降低一维，大大减少计算量；对于无限域的模拟，与边界元法相比，不需要基本解即可自动满足无穷远处的辐射边界条件.林皋等［25－26］将综合考虑库水可压缩性和库底吸收条件，推导了动水压力的比例边界有限单元方程，并在频域和时域内进行了求解，将其应用于大坝－库水动力相互作用分析.Li［27］针对半无限等截面层状库水，对比例边界有限单元方程采用对角化技术，简化卷积计算，并用于时域大坝－库水动力相互作用分析.

高阶局部透射边界可以在保证较高计算效率的同时达到任意阶的计算精度，成为近十多年来无限域模拟中的一个研究热点［28］.然而，目前大部分高阶透射边界基本属于高频单向渐近边界，只能模拟行波的传播，无法模拟快衰波的能量传递［29］.对于半无限库水，存在一个截断频率，当激振频率低于截断频率时，水库中存在快衰波，这使得部分波动能量在未来得及向远处传播之前已经衰减.Prempramote和Song等［30］基于动力刚度的连分式双渐近解提出了一类高阶双渐近透射边界，该透射边界随着阶数的增加能够在全频范围内快速收敛到准确解，具有很高的计算精度和计算效率.王翔等［31］将该透射边界推广到边界离散的单元节点上，提出了动水压力波高阶双渐近透射边界，并基于通用大型商业有限元软件ABAQUS的重启动分析功能实现了该透射边界与有限元单法的顺序耦合分析模型，进行了重力坝－库水动力相互作用分析，结果表明该透射边界具有很高的精度，但由于模型基于重启动，无法体现高阶双渐近透射边界在计算效率上的优势.

本文将动水压力波高阶双渐近透射边界直接嵌入到近场有限元方程中，得到一个整体控制方程，建立了混凝土坝－库水动力相互作用的直接耦合分析模型.基于有限元开源软件框架体系OpenSees编程实现了直接耦合分析模型，并将其应用于重力坝和拱坝与库水的动力相互作用分析.

2 混凝土坝－库水系统运动方程

典型的混凝土坝－库水系统如图1所示，其中向上游无限延伸的库水通过一个竖直截断边界被分割成近场和远场两个部分.具有不规则形状的近场库水与混凝土大坝构成广义结构，通过有限单元离散；远场规则库水可以简化成等高或者等截面的半无限层状介质，如图2所示，通过比例边界有限单元模拟，其相似中心取在下游无穷远处.

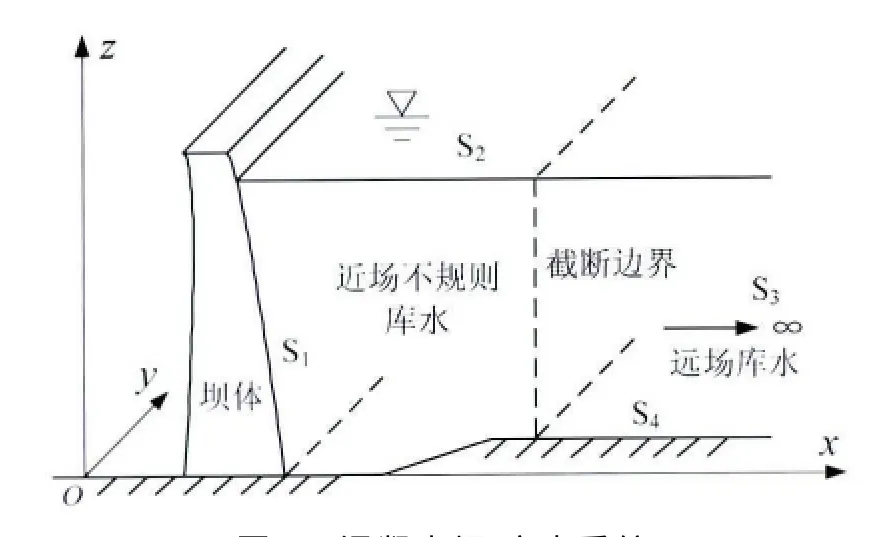
图1 混凝土坝－库水系统Fig.1 Concrete dam－reservoir system

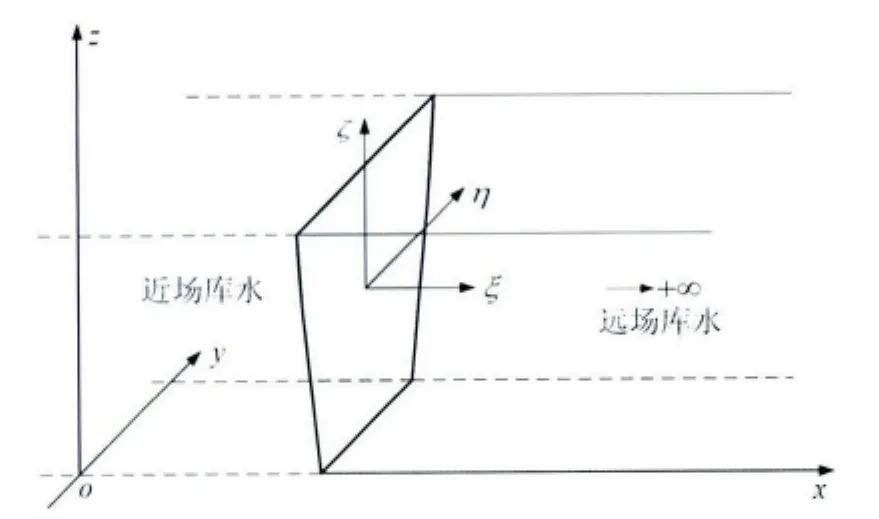
图2 比例边界有限元法应用于半无限水库Fig.2 SBFEM for semi－infinite reservoir

鉴于本文主要研究透射边界的影响，不考虑材料阻尼，则混凝土坝和近场库水系统的有限元耦合方程可以写成如下分块形式

式中，u和p分别表示位移和动水压力，和分别表示位移和动水压力对时间的两次导数；［M］为质量矩阵，［K］为刚度矩阵，［Q］为混凝土坝与库水之间的耦合矩阵，｛f｝为外荷载向量.下标s表示坝体结构节点自由度，下标f表示不包含截断边界的库水节点自由度，下标b表示截断边界节点自由度.远场半无限库水对近场的影响通过作用力－｛r｝表现.

库水按理想声学流体介质处理，不考虑库底的吸收作用，竖直截断边界的半无限等高或等截面层状介质动水压力波的比例边界有限单元方程如下式［31］

［E0］｛p｝，ξξ－ ［E2］｛p｝－ ［M0］｛p｝，tt＝0，（2）式中 ｛p｝为动水压力，｛p｝，ξξ表示动水压力对比例边界坐标ξ的二次偏导，｛p｝，tt表示动水压力对时间的二次导数，系数矩阵 ［E0］、［E2］和［M0］的定义参见文献［31］.值得指出的是，对于半无限等高或等截面层状介质，［M0］和［E0］存在如下关系

式中，c为动水压力波波速.在竖直截断边界上应用虚功原理，可得

式中 ｛R（ω）｝和 ｛P（ω）｝分别为截断边界上的等效节点荷载和节点动水压力在频域内的幅值.根据动力刚度 ［S∞（ω）］的定义，有

综合考虑式（4）和式（5），式（2）可以改写成频域动力刚度表示的比例边界有限单元方程

3 直接耦合分析模型的建立

3.1 动力刚度的连分式双渐近解

式（6）表示的比例边界有限单元方程可以通过模态变换的方式解耦.考虑如下广义特征值分解

式中［Λ2］为对角矩阵，其对角元素为λ2j，h为层状介质高度.对式（2）左乘h［Φ］T，右乘h［Φ］，并利用式（3）和式（7）可以得到如下解耦的比例边界有限单元方程

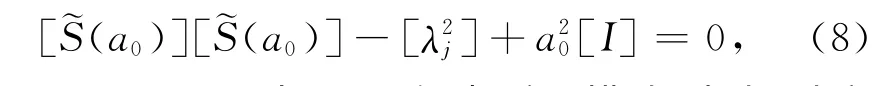
式中a0＝ωh／c为无量纲频率，模态动力刚度［~S（a0）］为对角矩阵，其定义如下

根据文献［31］的结果，单一模态的动力刚度的连分式双渐近解可以表示成

式中MH和ML分别为连分式高频和低频渐近阶数.其中式（10）和式（11）为高频渐近解，它通过使式（8）在高频极限a0→ ∞ 成立得到；式（13）和式（14）为低频渐近解，它通过使高频渐近解的残余项（式（12）表示）在低频极限a0→0成立得到.该连分式双渐近解能在全频范围内逼近动力刚度的准确解，因而能够同时模拟行波和快衰波的传播.

为了验证连分式双渐近解的精度及其快速收敛到动力刚度准确解的特性，在频域内将模态动力刚度的连分式双渐近解与准确解进行对比，其结果见图3.从中可以看出，除了在截断频率附近的精度稍差外，MH＝ML＝2的双渐近解基本能在全频范围内逼近动力刚度的准确解；继续增加连分式阶数至MH＝ML＝4，其渐近解在全频范围内快速收敛到准确解.综上，连分式双渐近解能够快速收敛到动力刚度的准确解，仅需要较少的阶数就能达到良好的结果.根据图3给出的结果，在时域分析中，可以选取阶数为MH＝ML＝4的透射边界进行计算.

3.2 高阶双渐近透射边界

参照文献［31］的构建高阶透射边界的思路，首先将模态动力刚度的连分式双渐近解式（10）～（14）改写成矩阵形式，然后对其左乘 ［Φ］T／h、右乘［Φ］后依次代入式（5），并引入辅助变量，最后再进行傅里叶逆变换即可得时域动水压力波高阶双渐近透射边界的表达式为

式中系数矩阵［C∞］和［A］定义如下

3.3 直接耦合分析模型

考虑MH阶和ML阶的双渐近透射边界，令高阶残余项取零.式（15）～式（19）表示的高阶双渐近透射边界直接建立在竖直截断边界离散节点之上，可以直接通过右端作用力｛r｝同近场有限元方程耦合.将式（15）～（19）代入近场有限元方程（1），即可得到考虑远场库水辐射阻尼的混凝土坝－库水系统动力相互作用的直接耦合分析模型的控制方程

式中广义系数矩阵 ［Mh］、［Ch］和［Kh］定义如下（分块矩阵用黑体字母表示）

图3 模态动力刚度的双渐近解（a）实部；（b）虚部.Fig.3 Continued fraction solution for modal dynamic stiffness（a）Real part；（b）Imaginary part.

其中分块矩阵定义为

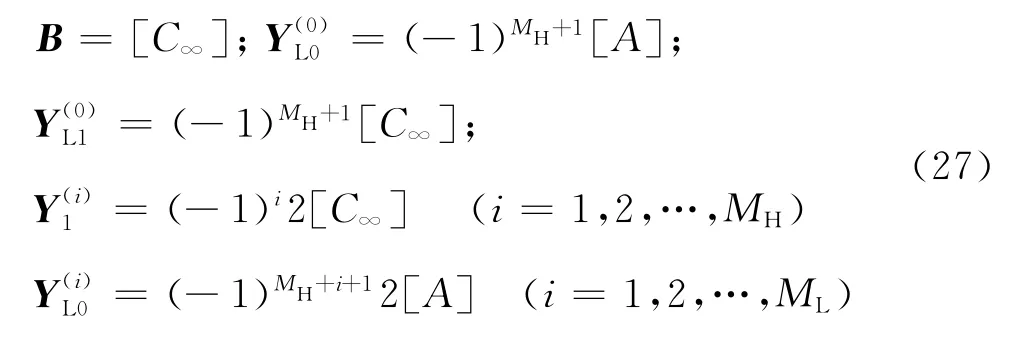
广义未知向量与广义外荷载向量分别为

4 算 例

OpenSees是由美国加州伯克利大学主研发的有限元开源软件框架体系，它基于面向对象的编程思想，具有丰富的单元库和材料库，并且可以方便地添加自定义单元和材料.借助于OpenSees开源代码的优势，作者在OpenSees中嵌入了流固耦合分析程序和高阶双渐近透射边界，实现了大坝－库水动力相互作用直接耦合分析程序.采用以下算例进行模型验证，计算中，时步积分法采用Newmark－β法，其中γ＝0.5，β＝0.25，即平均常加速度法.

4.1 重力坝算例

图4 重力坝－库水系统（a）几何模型；（b）有限元网格.Fig.4 A gravity dam－reservoir system（a）Geometory；（b）Finite element mesh.

选取文献［31］中的重力坝算例，重力坝和半无限库水耦合分析系统如图4所示.重力坝同近场不规则库水统一采用8节点二次单元离散，其中坝体单元52个，库水流体单元156个，竖直截断边界采用13个二次线单元离散.材料参数取值如下：坝体混凝土弹性模量E＝35GPa，泊松比ν＝0.2，质量密度ρ＝2400kg／m3；动水压力波波速c＝1438.7m·s－1，库水密度ρf＝1000kg·m－3.

根据前面分析的结果，选取透射边界阶数MH＝ML＝4.为了验证透射边界的精度，采用有限元扩展网格解作为参考解.在扩展网格模型中，远场库水有限单元离散的长度为7200m，动水压力波在该范围内往返传播的时间约为10s（对应的无量纲时间tc／h约为90），即扩展网格模型的前10s计算结果有效.计算时步取0.01s，对应的无量纲时间约为0.09.

考虑重力坝基底受到顺河向的三角脉冲加速度荷载作用，图5是按无量纲时间定义的三角脉冲时程曲线.重力坝坝底动水压力时程如图6所示，可以看出，透射边界阶数为MH＝ML＝4的直接耦合分析模型的计算结果与扩展网格模型提供的参考解几乎完全吻合，表明直接耦合分析模型具有很高的计算精度.从计算耗时上看，直接耦合分析模型耗时6s，而扩展网格模型耗时约258s，表明该模型具有很高的计算效率.

图5 三角脉冲荷载时程曲线Fig.5 Time history of triangular impulse

4.2 拱坝算例

考虑如图7所示的拱坝－库水系统，混凝土拱坝坝高H＝265m.计算中，分别将透射边界置于离坝体1倍坝高和0.5倍坝高处，即近场库水离散范围L分别取H和0.5H.坝体和近场库水均采用20节点六面体单元模拟，其中坝体单元192个，近场库水单元分别为640个和320个；坝体和库水的交界面采用64个8节点界面单元模拟，竖直截断边界采用64个8节点二次单元模拟.计算中，坝体混凝土和库水的材料参数同重力坝算例.

计算中，选取透射边界阶数为MH＝ML＝4，计算步长为0.02s.依然采用有限元扩展网格模型作为参考解，远场库水的离散范围为7200m（约27倍坝高），即扩展网格的前10s计算结果有效.

考虑拱坝基底受到顺河向的El Centro地震波荷载作用，其中El Centro地震波的加速度时程曲线如图8所示.图9给出了直接耦合分析模型与扩展网格模型前10s的计算结果，可以看出，即使将透射边界置于0.5倍坝高处，直接耦合模型给出的计算结果仍同扩展网格模型的解基本吻合.因此，在直接耦合分析模型中，可以减少近场库水的离散范围，节约计算时间.从计算耗时看，近场库水离散范围分别为1倍坝高和0.5坝高时，计算耗时为65s和51s，而扩展网格模型计算耗时1847s，拱坝算例同样体现了直接耦合模型具有很高的计算效率.

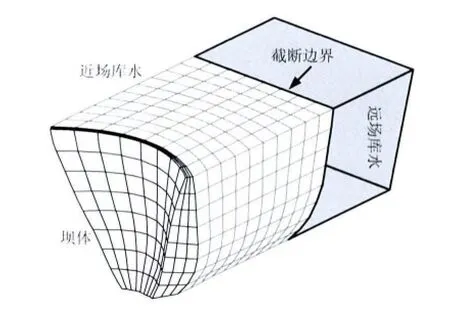
图7 拱坝库水系统Fig.7 An arch dam－reservoir system

图8 El－Centro地震波时程曲线Fig.8 Time history of El Centro earthquake

5 结 论

高阶双渐近透射边界能够在低频和高频范围内迅速地逼近准确解，具有良好的收敛性能和计算效率.本文将高阶双渐近透射边界同有限单元法直接耦合起来，建立了时域大坝－库水动力相互作用的直接耦合分析模型，由于该模型的整体控制方程保留了近场有限元方程系数矩阵对称稀疏的特点，可以方便地利用通用有限元的求解器.基于开源软件框架体系OpenSees，作者编写了时域大坝－库水相互作用的直接耦合分析程序，并且应用于大坝－库水动力相互作用分析.重力坝和拱坝的算例表明，该模型具有很高的精度和较高的计算效率，并且可以减少近场库水的离散范围，适用于模拟长时间地震荷载作用下的动水压力波响应.

图6 三角脉冲荷载作用下重力坝坝底动水压力时程Fig.6 Hydrodynamic pressure at heel of the gravity dam under triangular impulse

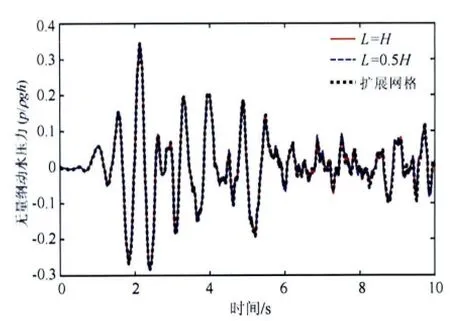
图9 地震波作用下拱坝坝底动水压力时程Fig.9 Hydrodynamic pressure at heel of the arch dam under El Centro earthquake

（

）

［1］ Zhang C H，Pan J W，Wang J T.Influence of seismic input mechanisms and radiation damping on arch dam response.SoilDynamicsandEarthquakeEngineering，2009，29（9）：1282－1293.

［2］ Humar J L，Jablonski A M.Boundary element reservoir model for seismic analysis of gravity dams.Earthquake Engineering＆StructuralDynamics，1988，16（8）：1129－1156.

［3］ 徐艳杰，张楚汉，金峰.非线性拱坝－地基动力相互作用的FE－BE－IBE模型.清华大学学报（自然科学版），1998，38（11）：100－104.Xu Y J，Zhang C H，Jin F.Model of FE－BE－IBE coupling for soil－structure interaction on nonlinear response of arch dams.JournalofTsinghuaUniversity（Sci＆Tech）.（in Chinese），1998，38（11）：100－104

［4］ Liu X，Xu Y，Wang G，et al.Seismic response of arch dams considering infinite radiation damping and joint opening effects.EarthquakeEngineeringandEngineeringVibration，2002，1（1）：65－73.

［5］ 徐艳杰，牟海磊，张楚汉，et al.汶川地震中宝珠寺重力坝地震响应的三维有限元模拟.地球物理学报，2012，55（1）：293－303.Xu Y J，Mu H L，Zhang C H，et al.3Dfinite element modeling of seismic response of Baozhusi gravity dam inMs8.0Wenchuan Earthquake.ChineseJ.Geophys.（in Chinese），2012，55（1）：293－303

［6］ 程惠红，张怀，朱伯靖，et al.新丰江水库地震孔隙弹性耦合有限元模拟.中国科学：地球科学，2012，42（6）：905－916.Cheng H H，Zhang H，Zhu B J，et al，Finite element investigation of the poroelastic effect on the Xinfengjiang Reservoir－Triggered earthquake.SciChinaEarthSci，（in Chinese），2012，42（6）：905－916.

［7］ Westergaard H M. Water pressure on dams during earthquakes.Transactions of the American Society of Civil Engineering，1933，98：418－433.

［8］ 杜修力，王进廷.动水压力及其对坝体地震反应影响的研究进展.水利学报，2001，（7）：13－21.Du X L，Wang J T.Review of studies on the hydrodynamic pressure and its effects on the seismic response of dams.JournalofHydraulicEngineering（in Chinese），2001，（7）：13－21.

［9］ 徐世浙.地球物理中的有限单元法.北京：科学出版社，1994：260－277.Xu S Z，The finite element method in Geophysics （in Chinese），Beijing：Science Press，1994：260－277.

［10］ 冯德山，陈承申，王洪华.基于混合边界条件的有限单元法GPR正演模拟.地球物理学报，2012，55（11）：3774－3785.Feng D S，Chen C S，Wang H H，Finite element method GPR forward simulation based on mixed boundary condition.ChineseJ.Geophys.（in Chinese），2012，55 （11）：3774－3785.

［11］ 李伟华，刘清华，赵成刚.饱和多孔介质三维时域黏弹性人工边界与动力反应分析的显式有限元法.地球物理学报，2010，53（10）：2460－2469.Li W H，Liu Q H，Zhao C G，Three－dimensional viscousspring boundaries in time domain and dynamic analysis using explicit finite element method of saturated porous medium.ChineseJ.Geophys.（in Chinese），2010，53（10）：2460－2469.

［12］ Lan H，Zhang Z.Three－Dimensional Wave－Field Simulation in Heterogeneous Transversely Isotropic Medium with Irregular Free Surface.BulletinoftheSeismologicalSociety ofAmerica，2011，101（3）：1354－1370.

［13］ Lan H Q，Zhang Z J.Comparative study of the free－surface boundary condition in two－dimensional finite－difference elastic wave field simulation.JournalofGeophysicsandEngineering，2011，8（2）：275.

［14］ 兰海强，刘佳，白志明，VTI介质起伏地表地震波场模拟，地球物理学报，2011，54（8）：2072－2084，Lan H.Q.，Liu J.，Bai Z.M.，Wave－field simulation in VTI media with irregular free surface.ChineseJ.Geophys.（in Chinese），2011，54（8）：2072－2084.

［15］ Givoli D.Non－reflecting boundary conditions.Journalof ComputationalPhysics，1991，94（1）：1－29.

［16］ 邵秀民，蓝志凌.各向异性弹性介质中波动方程的吸收边界条件.地球物理学报，1995，38（S1）：56－73.Shao X M，Lan Z L.Absorbing boundary conditions for anisotropic elastic wave equations.ChineseJ.Geophys.（in Chinese），1995，38（S1）：56－73.

［17］ 廖振鹏，周正华，张艳红.波动数值模拟中透射边界的稳定实现.地球物理学报，2002，45（4）：533－545.Liao Z P，Zhou Z H，Zhang Y H.Stable implementation of transmitting boundary in numerical simulation of wave motion.ChineseJ.Geophys.（in Chinese），2002，45（4）：533－545.

［18］ Chen J Y，Bording R P，Liu E R et al.The application of the nearly optimal sponge boundary conditions for seismic wave propagation in poroelastic media.JournalofSeismic Exploration，2010，19（1）：1－19.

［19］ Yang D H，Wang S Q，Zhang Z J et al.n－Times Absorbing Boundary Conditions for Compact Finite－Difference Modeling of Acoustic and Elastic Wave Propagation in the 2DTI Medium.BulletinoftheSeismologicalSocietyofAmerica，2003，93（6）：2389－2401.

［20］ Zienkiewicz O C， Bettess P. Fluid－structure dynamic interaction and wave forces：An introduction to numerical treatment.InternationalJournalforNumericalMethodsin Engineering，1978，13（1）：1－16.

［21］ Küçükarslan S，Coskun S B，TaskIn B.Transient analysis of dam－reservoir interaction including the reservoir bottom effects.JournalofFluidsandStructures，2005，20（8）：1073－1084.

［22］ Antes H，Von Estorff O.Analysis of absorption effects on the dynamic response of dam reservoir systems by boundary element methods.EarthquakeEngineering＆Structural Dynamics，1987，15（8）：1023－1036.

［23］ Soares Jr D，von Estorff O，Mansur W J.Efficient non－linear solid－fluid interaction analysis by an iterative BEM／FEM coupling.InternationalJournalforNumericalMethodsin Engineering，2005，64（11）：1416－1431.

［24］ Song C M，Wolf J P.The scaled boundary finite－element method－alias consistent infinitesimal finite－element cell method－for elastodynamics.ComputerMethodsinApplied MechanicsandEngineering，1997，147（3－4）：329－355.

［25］ Lin G，Du J G，Hu Z Q.Dynamic dam－reservoir interaction analysis including effect of reservoir boundary absorption.ScienceinChinaSeriesE：TechnologicalSciences，2007，50：1－10.

［26］ Lin G， Wang Y，Hu Z Q.An efficient approach for frequency－domain and time－domain hydrodynamic analysis of dam－reservoir systems.EarthquakeEngineering＆Structural Dynamics，2012，41（13）：1725－1749.

［27］ Li S M.Diagonalization procedure for scaled boundary finite element method in modeling semi－infinite reservoir with uniform cross－section.InternationalJournalforNumerical MethodsinEngineering，2009，80（5）：596－608.

［28］ Givoli D. High－order local non－reflecting boundary conditions：a review.WaveMotion，2004，39（4）：319－326.

［29］ Geers T. Singly and doubly asymptotic computational boundaries.In：TL G，editor.Proceedings of the IUTAM Symposium on Computational Methods for Unbounded Domains.Dordrecht：Kluwer Academic Publishers；1998.p 135－141.

［30］ Prempramote S，Song C M，Tin－Loi F，et al.High－order doubly asymptotic open boundaries for scalar wave equation.InternationalJournalforNumericalMethodsinEngineering，2009，79（3）：340－374.

［31］ Wang X，Jin F，Prempramote S，et al.Time－domain analysis of gravity dam－reservoir interaction using high－order doubly asymptotic open boundary.Computers＆Structures，2011，89（7－8）：668－680.