三维频率域航空电磁反演研究

刘云鹤，殷长春

吉林大学地球探测科学与技术学院，长春 130026

1 引 言

三维电磁法正反演技术近年发展较快，已经开始从单纯的理论研究走向实际应用.三维航空电磁模拟需要在每个源位置单独做一次正演导致计算量过大，无法实现快速数值计算，所以其数据反演相对于其他固定源或者源位置较少的电磁法发展缓慢.最近，Cox等提出一种利用航空电磁系统“footprint”概念来减小反演模型规模的算法［1］.利用该算法，整个反演区域被离散成每个测点下方“footprint”大小的子区域，而该点航空电磁响应和数据的灵敏度矩阵只在这个子区域内计算.另外，Oldenburg等利用矩阵分解技术实现了多发射源电磁法的快速正反演［2］.这两种技术加速了航空电磁正演的过程，进而使得大规模三维航空电磁反演成为可能.然而，在正演速度提高的基础上我们还需要寻找一种稳定和精确的最优化算法以实现三维航空电磁的高效反演.

过去的十多年中，各种优化算法被引用到求解多维情况下的最小值问题.主要包括Gauss－Newton（GN）算法、非线性共轭梯度法（NLCG）和拟牛顿法（QN）等.这几种方法在内存需求和计算速度上可以满足三维电磁反演的需要.Mackie等、Siripunvaraporn等和林昌洪等利用GN方法从事大地电磁的三维反演［3－5］，而 Sasaki和 Oldenburg 等 利 用 GN 方 法 实现了三维航空电磁数据反演［2，6］.基于梯度的直接最优化算法NLCG和有限内存L－BFGS（标准的QN方法）都是节省内存的有效反演方法，目前被广泛应用于大地电磁、海洋电磁和地面可控源类电磁法的数据反演中［7－16］.对于大规模的三维数据反演，为了节省内存和计算时间，上述三种方法都非显式地计算灵敏度矩阵，而是通过伴随方法计算灵敏度矩阵和向量的乘积.GN方法通常利用预处理的共轭梯度法求解反演方程（PCG），在每次的共轭梯度法迭代过程中需要两次额外的伴随正演来计算灵敏度矩阵与向量的乘积.为了减少计算量一般都采用截断的方式来终止共轭梯度的迭代过程.NLCG和L－BFGS方法在每次迭代过程中只需要计算一次梯度，即只需要一次正演和一次伴随正演.与GN方法相比，NLCG和L－BFGS方法每次迭代的正演计算量较少，然而反演收敛速度较慢.据Schwarzbach和Haber等的研究，GN方法在进行伴随正演过程中需要存储每个源的全域解向量.当发射源较多时，有限的内存空间无法存储所有源的全域解向量，因此该方法不适合多发射源的电磁反演［17］.Newman和Boggs曾对NLCG和L－BFGS的电磁反演效果进行对比［9］.然而，其步长搜索存在缺陷，导致 LBFGS算法的迭代步长总是不能达到最优理论值1；由此，L－BFGS较之于NLCG在反演效果上的优越性没有得到体现.本文中，我们采用Egbert和Kelbert提出的改进NLCG步长搜索技术及Nocedal和 Wright提出的L－BFGS步长搜索技术进行三维航空电磁数据反演［18］，并以垂直磁偶极子发射多分量观测方式为例，比较NLCG和L－BFGS在三维航空电磁反演中的应用效果.

2 正演模拟

三维频率域航空电磁正演计算基于下面的二次电场的偏微分方程：

其中Ep为发射偶极在背景电导率σb中产生的一次背景场，Es为二次电场，σ为模型电导率，ω为角频率，μ为磁导率［19］.总的电场为E＝Ep＋Es，而磁场H由公式

得到.本文采用交错网格有限差分技术离散方程（1），最终形成的大型方程组采用拟最小残差法（QMR）求解.图1给出的正演模型采用Newman和Alumbaugh在1995年给出的模型［19］.发射和接收装置离地面20m，发射－接收源距为10m.我们考虑水平共面HCP与垂直共轴VCX两种装置，发射频率为900Hz.计算区域采用长方体单元进行离散，网格数为50×50×40.图2中给出本文算法与Newman和Alumbaugh结果的比较.由图可以看出，本文的结果与Newman和Alumbaugh的结果整体吻合很好.虚部在异常体正上方的误差稍大，但仍小于1ppm.

图1 三维航空电磁正演模型Fig.1 3Dearth for AEM modeling（Newman and Alumbaugh，1995）

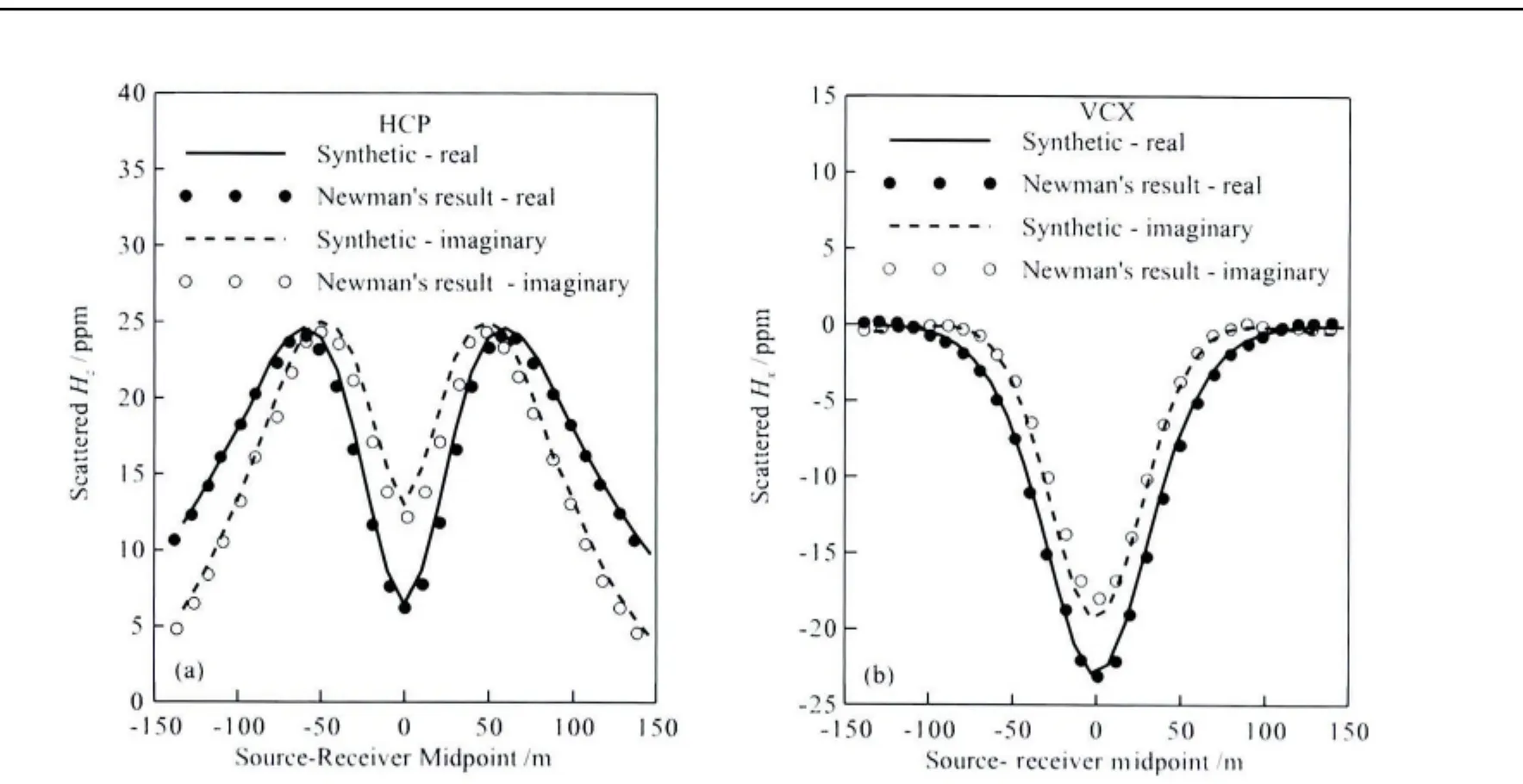
图2 三维频率域航空电磁正演结果验证Fig.2 Model results for 3Dfrequency－domain AEM systems in comparison to those of Newman and Alumbaugh（1995）

3 反演理论

3.1 正则化

依据Egbert和Kelbert的阐述［15］，本文通过最小化目标函数

来解决正则化反演问题.上式中，m是M维地球电导率模型参数向量，d是Nd维数据向量，Cd是数据方差矩阵，f（m）为正演算子，m0是先验或初始估计模型，λ是正则化因子，Cm是模型方差矩阵.通过变换（3）式可以进一步简化.假设

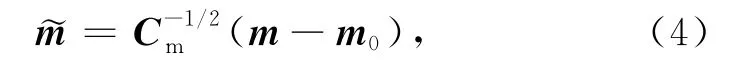
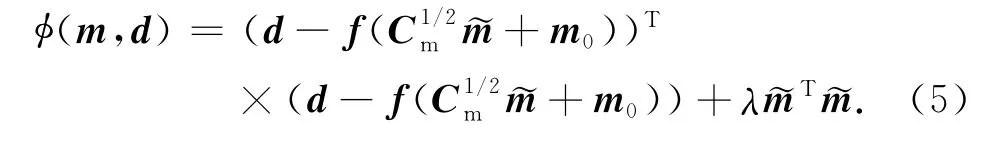
目标函数的梯度为

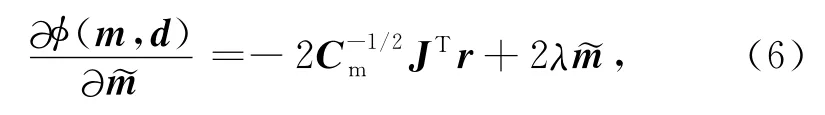
其中J是灵敏度矩阵，最终

的模型参数可以通过

来计算.为简便起见，我们在后面的讨论中忽略模型参数上面的波浪线.

3.2 反演约束

与传统的模型约束方式不同，本文中的Cm不是仅考虑每个离散单元和其相邻的单元之间的影响，而是将整个模型所有元素之间的相互影响关联起来.Cm的计算采用Egbert和Siripunvaraporn等提出的一种递归自回归算法［20－21］.该算法的实质为求解一个扩散方程，实现过程为，先在x、y、z三个方向每个参数都在与前一个参数和光滑因子的乘积求和后，再与光滑因子相乘加到下一个参数，这样便将所有参数关联起来，然后对已经光滑的所有参数按z、y、x方向再反向光滑一遍.（6）式中，C－1／2m除了通过正则化因子λ对模型电导率进行约束外，还直接约束目标函数梯度表达式中的数据梯度部分.类似的直接修正梯度方法已得到广泛应用.Plessix和Mulder提出用变尺度的趋肤深度幂指数对梯度进行修正［22］；Mackie和Newman等将近似的Hessian矩 阵 作 为 梯 度 的 预 处 理 算 子［9，23－24］；Avdeev 和Avdeeva提出了一种附加正则化方法来修正梯度［14］.这些修正梯度的方法可以使浅层异常的反演变得稳定，加速了反演过程.本文中，我们进一步深入研究中光滑因子对反演结果的影响.进而，为改变反演的稳定性和速度，我们在反演中采用了变化的光滑因子.在反演初始阶段采用大的光滑因子以确定准确的异常体空间位置；而当数据拟合差下降缓慢时，则通过减小光滑因子获得准确的异常体大小和电阻率值.

3.3 反演流程

NLCG方法反演流程：

1）令i＝1，选择初始模型mi及模型光滑因子，并计算ri＝－Δφ（mi，d）；

2）如果‖ri‖很小则停止，否则令M为预处理矩阵；

3）搜索αi使φ（mi＋αiui，d）最小化.当步长αi太小时减小正则化因子λ，如果λ达到阀值则反演终止；

4）令mi＋1＝mi＋αiui和ri＋1＝－Δφ（mi＋1，d）；

5）如果‖ri＋1‖很小则停止，否则向下继续执行；

L－BFGS方法反演流程：

1）令i＝1，选择初始模型mi、模型光滑因子及初始对称正定矩阵Hi，设定导数控制精度ε＞0；

2）计算ri＝－Δφ（mi，d）.如果 ‖ri‖ ≤ε，则迭代终止，输出最终解mi；

3）否则，令ui＝Hiri，搜索αi.当步长αi太小时减小正则化因子λ.如果λ达到阀值则反演终止；

4）令mi＋1＝mi＋αiui，如果 ‖ri＋1‖ ≤ε，则得到最终解mi＋1；

6）令i＝i＋1，然后跳到2）.

NLCG和L－BFGS反演过程中均采用自适应方式选择正则化因子λ.具体实现方式为：当数据拟合差下降小于0.002时，正则化因子λ变为原来的十分之一.正则化因子λ在反演中约束步长的大小，每减小一次λ导致正则化部分在目标函数的比重变小，模型修正空间变大，可以搜索较大的步长.当λ减小到阀值时，反演基本只拟合数据部分，如果数据拟合差仍缓慢下降，说明目标函数值达到极小.另外，如果目标函数梯度过小，目标函数值也达到极小.因为即使是理论数据也不能使数据拟合差总降低到0，因此本文的理论数据反演并没有给定数据拟合差阀值，而是采用λ和梯度是否达到阀值确定终止反演.

NLCG和L－BFGS反演过程中需要计算目标函数的梯度和搜索步长.下面分别介绍梯度的计算方法和步长的搜索方法.

3.4 梯度计算

有限差分方法的最终方程组可以写成

其中K为系数矩阵，s为方程（1）的右端源项.将（8）

式两端对第k个模型参数mk求导得到［9］

将方程（1）中源项表达式带入（9）式并进行化简，得到

将方程（2）简写为Hs＝LEs，其中L为空间插值算子，则磁场的导数为

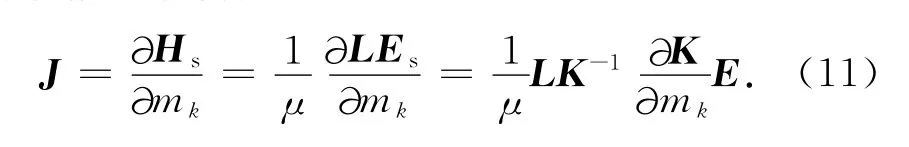
假设如下Nd×M维矩阵

则有

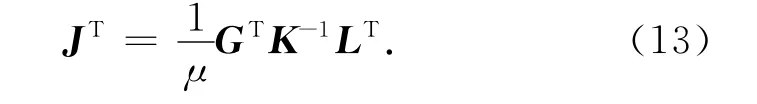
将（13）式带入（6）式，则（6）式右端第一项变为

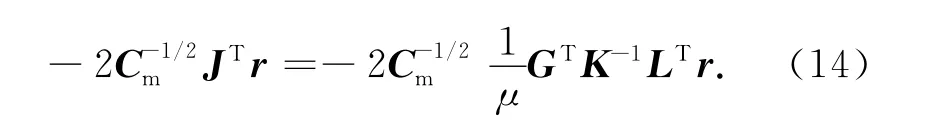
令

则可以通过求解伴随正演

得到v.将v带入到（14）式中就可以得到数据部分的梯度值，而模型部分的梯度值是解析的，这样只通过一次正演和一次伴随正演就可计算出目标函数的梯度.

3.5 步长搜索

与其他可以通过解析方法得到步长的方法（比如共轭梯度法等）不同，NLCG和L－BFGS两种方法需要通过线性搜索得到反演迭代步长.NLCG方法需要沿负梯度及其共轭方向搜索步长；而L－BFGS方法则沿经近似Hessian矩阵的逆修正后的负梯度方向搜索步长.最优化过程的步长一般需要满足如下充分下降条件

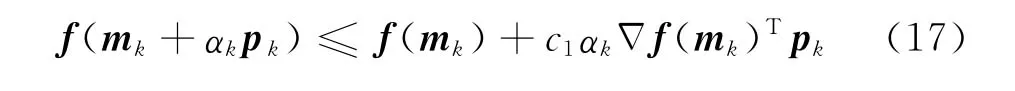
和曲率条件

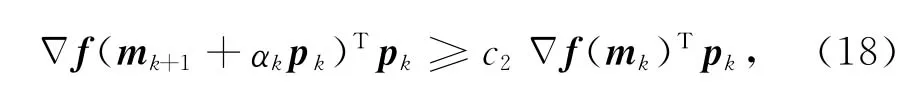
其中，f为正演算子，mk为第k次迭代的模型参数向量，αk为迭代步长，p为搜索方向，c1和c2为常数，满足0＜c1＜c2＜1，k为迭代次数.这两种条件统称为 Wolfe条件.在实际应用中，一般取c1＝0.0001；对于GN或者 QN方法，c2＝0.9，而对于非线性共轭梯度法c2＝0.1.另外，还存在一种逆向追踪方法（back tracing）用来约束反演步长，其作用和（18）式类似.逆向追踪法的基本步骤为：选取一个在0到1之间变化的值，将其与未满足充分下降条件的步长做乘积，直到步长满足充分下降条件（17）为止.实际反演中，通常选取多次函数插值方式来进行逆向追踪［18］.目前，NLCG方法广泛采用充分下降条件和逆向追踪方法组合约束反演步长，而LBFGS利用充分下降条件和曲率条件来约束步长.

本文采用的NLCG步长搜索方式为：

1）第一次初始迭代步长设为＝0.001.以后每次迭代中，初始步长首先设为

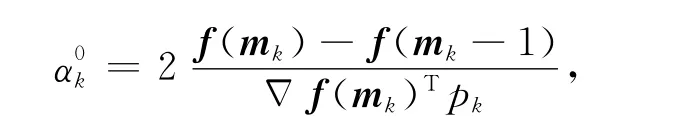
2）利用二次方函数插值技术得到步长.如果满足充分下降条件（17），则判断f（mk＋）是否成立.如果成立则取，否则取；如果不满足充分下降条件（17），则利用三次方函数插值技术进行逆向追踪.

L－BFGS步长搜索方式为：

1）每次迭代反演初始步长均为＝1，判断此步长是否满足Wolfe条件，如果满足则取初始步长为该次迭代步长；

2）否则，如果初始步长不满足Wolfe条件，则利用线性搜索算法求取迭代步长.具体算法包括两层循环：外层循环为将整个步长求取区间［0，αmax］利用插值技术分成数个子区间，然后依次在每个子区间中搜索满足Wolfe条件的步长，当找到满足条件的步长后循环自动结束；内层循环为在每个子区间搜索满足Wolfe条件的步长时，利用二次方函数插值以及三次方函数插值技术计算迭代步长αj，如果得到的步长不合适，则利用该步长更新子区间的边界，然后在更新后的子区间，重复上面计算步长的步骤.内层循环直到找到合适步长或者在子空间内已搜索完毕后终止.如果在区间［0，αmax］中得不到满足Wolfe条件的步长αk，则重新计算新的目标函数值和导数，然后重新搜索.pk）＜f（mk＋

4 理论数据反演

为了进行理论数据的反演测试，本文首先设计一个电阻率为100Ωm的背景模型，并将其离散成28×28×25个网格，其中在x和y方向包括8个扩边，在z方向包括4个向下的扩边和8个空气层.模型中心区域三个方向的网格边长均为10m，扩边的大小依次为20m，40m，80m，160m.前两个空气层在z方向的长度均为10m，上方的空气层厚度的递增系数为3，最顶层厚度为30000m.观测方式选择水平共面装置（HCP），发射与接收装置的高度设为20m，发射频率为900Hz和5000Hz，观测数据包含三个方向的磁场分量.测点间距在x和y方向均为20m，总计100个观测点.根据“footprint”概念，某测点的响应大小只与其下方一定范围的地电模型相关［1］.在反演大区域数据时可以将整个大区域离散成每个测点下方的“footprint”大小的模型进行灵敏度矩阵或灵敏度矩阵与向量乘积的计算.由于本文选取的模型大小与所选的航空电磁系统的“footprint”尺度接近，因此本文算例分析实质上反应了航空电磁基于“footprint”反演技术的效率.

反演测试的第一个模型为将上述背景模型中嵌入一个30Ωm的异常体.异常体顶部埋深为20m，三个方向的长度均为40m（见图1）.反演开始时，式（1）中的正则化因子λ设为10，且在反演过程中采用自适应方式递减.当正则化因子减小到0.0001时，数据拟合误差基本不再变化，反演过程自动终止.图3给出理论数据的反演结果.从图可以看出，当选择光滑因子为0.3时，L－BFGS和NLCG的反演结果中，异常体的电阻率比较接近真实电阻率值，但是位置均较真实位置更靠近地表；当选择光滑因子为0.5时，L－BFGS和NLCG的反演结果中异常体的位置接近正演模型中的异常体真实位置，但是反演电阻率值与真实值偏差较大，且异常分布范围较广；当光滑因子初始值选为0.5，而在数据拟合差下降小于0.002时，光滑因子调整到0.3（判断条件与正则化因子自适应算法相同，但光滑因子先于正则化因子变化），发现L－BFGS和NLCG的反演结果中，异常体的位置和电阻率较光滑因子分别为0.3和0.5时更接近模型真实值.对于图3中所选的三种光滑因子，L－BFGS均比NLCG方法得到的结果准确.另外，从图4给出的数据拟合误差随迭代次数的变化可以看出，L－BFGS方法的数据拟合差下降速度比NLCG快.如果从正演次数来考虑反演效率，L－BFGS方法较NLCG方法体现出明显优势.事实上，当反演迭代步长为1时，L－BFGS方法每次迭代需要的正演次数为2次；而对于图4中迭代步长不为1的情况，L－BFGS每次迭代需要进行4次正演.综合起来，L－BFGS每次反演迭代大约需要作2.2次正演计算.根据Newman等的结论，NLCG每次反演迭代至少需要3次正演［7］.

图3 单个异常体模型及不同光滑因子L－BFGS和NLCG反演结果Fig.3 Single anomalous target model and L－BFGS and NLCG inversions for different smoothing parameters

图4 单个异常体反演的数据拟合误差及反演步长随迭代次数变化Fig.4 Data misfit and model modification vs.iterations for single anomalous target model

为了进一步在复杂模型中比较这两种反演方法的有效性，我们将图3中的单个异常体替换为8个异常体.如图5a所示，靠近地表的4个异常体大小为50m×50m×10m，电阻率分别为30Ωm和300Ωm；另外4个异常体埋深均为30m，大小为50m×50m×30m，电阻率分别为20Ωm和2000Ωm.对于这个模型，正则化因子λ在反演开始时设为10000，最小值仍为0.0001.反演过程中采用变光滑因子0.5～0.3.比较图5b和5c中的反演结果可以看出，LBFGS较NLCG方法更好地恢复了真实模型.特别是对地下高阻异常的反映，L－BFGS和NLCG方法存在较大差异.NLCG方法没有得到高阻异常的准确消息，而L－BFGS方法基本上确定了高阻异常的位置和形状.从图5中还可以看出，即使是利用LBFGS方法，地下高阻异常的电阻率也只反演到300Ωm左右，远低于真实的2000Ωm；而NLCG方法只反演到了170Ωm左右，距离真实值差距更大.Oldenburg等认为这种现象的出现是正常的，因为利用感应源和磁场数据本质上很难反演出高阻异常体［2］.特别是对于航空电磁，由于发射与接收机距地面均有一定距离，电磁响应的体积效应会掩盖高阻异常体信息.图6中数据拟合差随反演迭代次数的变化特征表明NLCG方法过早地陷入了局部极小，导致反演结果没有L－BFGS方法的准确.

图5 8个异常体模型与L－BFGS和NLCG变光滑因子反演结果Fig.5 Model with 8anomalous targets and L－BFGS and NLCG inversion results for variable smoothing parameters

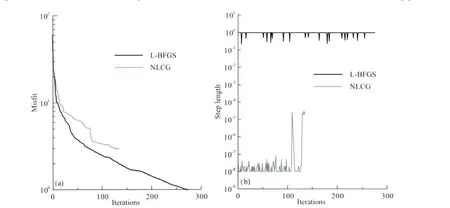
图6 8个异常体反演的数据拟合误差及反演步长随迭代次数变化Fig.6 Data misfit and model modification vs.iterations for the 8anomalous targets model

如3.3节所述，正则化因子λ的变化会增大模型修正空间，对于NLCG算法，导致反演步长变大，数据拟合差下降变快（拟合差下降曲线突变的地方）；而对于L－BFGS算法，其步长选择不受正则化因子变化的影响，数据拟合差曲线较为平缓.另外，从上述两个反演测试例子可以看出，L－BFGS方法基本采用1作为迭代步长；相比之下，NLCG方法的迭代步长特别小.其原因是NLCG方法的反演过程类似于最速下降法的线性优化算法，它需要很小的步长使反演收敛过程体现出超线性（super linear）反演算法特征.

5 反演效率分析

本文中所有的数值测试都是在PC上完成，其配备有Intel®CoreTMi3－2100CPU ＠3.10GHz和4GB RAM.两组模型反演结果表明，L－BFGS方法每次迭代大约需要2.2次正演，而NLCG大约需要3次正演计算.对于本文设计的航空电磁采集方式，每次正演包括100个位置的2个频率的子正演，共200次子正演.统计结果表明，每次正演大约耗时8min，即单个频率每个位置的子正演耗时大约需2.4s.以单个测点来考虑，每个频率100次迭代NLCG耗时约720s，而L－BFGS耗时大约需528s.本文中讨论的两种算法其内存占用量接近，均为100MB左右.本文中的算例进一步表明，如果设定相同的数据拟合差，L－BFGS较NLCG方法节约一半以上计算时间.

6 结 论

本文通过引入变化的光滑因子，改善了三维航空电磁数据反演的效果.反演结果中异常体的位置和电性较之于固定光滑因子条件下的反演结果更接近真实模型.以此为基础，通过对L－BFGS和NLCG方法的对比分析，发现L－BFGS方法不论是在反演速度上还是反演结果的准确性上都明显优于NLCG，因此更适合于处理大规模三维航空电磁数据的反演问题.由于采用的反演模型尺寸接近于航空电磁系统的“footprint”，所以本文单个测点的反演效率与目前广泛使用的“moving footprint”方法的反演效率相当［1］.然而，分析表明，对于本文设计的理论模型，即使是利用L－BFGS方法，每个测点单个频率仍需要10min以上的反演耗时，尚不能满足航空电磁海量数据的三维反演需求.本文的主要任务是寻找一种高效的最优化算法以实现精确、稳定的三维航空电磁反演，对于在此基础上如何进一步提高三维航空电磁正演速度及反演效率还需要深入研究.未来可通过结合模型分区和矩阵分解技术改善航空电磁正演速度，进而提高航空电磁数据的三维反演效率.这将是本研究团队的下一步研究目标.

（

）

［1］ Cox L H，Wilson G A，Zhdanov M S.3Dinversion of airborne electromagnetic data using a moving footprint.ExplorationGeophysics，2010，41（4）：250－259.

［2］ Oldenburg D W，Haber E，Shekhtman R.3Dinversion of multi－source time domain electromagnetic data. http：／／www.math.ubc.ca／～haber／Eldad＿Haber＿Web＿Page／Publications.html，2012［2013－03－21］.

［3］ Mackie R L，Madden T R.Three－dimensional magnetotelluric inversion using conjugate gradients.Geophys.J.Int.，1993，115（1）：215－229.

［4］ Sirepunvarpporn W，Egbert G D.Data space conjugate gradient inversion for 2－D magnetotelluric data.Geophys.J.Int.，2007，170（3）：986－994.

［5］ 林昌洪，谭捍东，佟拓.倾子资料三维共轭梯度反演研究.地球物理学报，2011，54（4）：1106－1113.Lin C H，Tan H D，Tong T.Three－dimensional conjugate gradient inversion of tipper data.ChineseJ.Geophys.（in Chinese），2011，54（4）：1106－1113.

［6］ Sasaki Y.Full 3－D inversion of electromagnetic data on PC.JournalofAppliedGeophysics，2001，46（1）：45－54.

［7］ Newman G A，Alumbaugh D L.Three－dimensional magnetotelluric inversion using non－linear conjugate gradients.Geophys.J.Int.，2000，140（2）：410－424.

［8］ Rodi W L，Mackie R L.Nonlinear conjugate gradients algorithm for 2－D magnetotelluric inversion.Geophysics，2001，66（1）：174－187.

［9］ Newman G A，Boggs P T.Solution accelerators for largescale three－dimensional electromagnetic inverse problems.InverseProblems，2004，20（6）：151－170.

［10］ Avdeev D B.Three－dimensional electromagnetic modelling and inversion from theory to application.Surv.Geophys.，2005，26（6）：767－799.

［11］ Haber E.Quasi－Newton methods for large－scale electromagnetic inverse problems.InverseProblems，2005，21（1）：305－323.

［12］ Plessix R E，Peter S.3DCSEM modeling and inversion in complex geologic settings.77thAnnual International Meeting，SEG，Expanded Abstracts，2007：589－593.

［13］ Kelbert A，Egbert G D，Schultz A.Non－linear conjugate gradient inversion for global EM induction：resolution studies.Geophys.J.Int.，2008，173（2）：365－381.

［14］ Avdeev D，Avdeeva A.3Dmagnetotelluric inversion using a limited－memory quasi－Newton optimization.Geophysics，2009，74（3）：F45－F57.

［15］ Egbert G D， Kelbert A. Computational recipes for electromagnetic inverse problems.Geophys.J.Int.，2012，189（1）：251－267.

［16］ 翁爱华，刘云鹤，贾定宇等.地面可控源频率测深三维非线性共轭梯度反演.地球物理学报，2012，55（10）：3506－3515.Weng A H，Liu Y H，Jia D Y，et al.Three－dimensional controlled source electromagnetic inversion using non－linear conjugate gradients.ChineseJ.Geophys.（in Chinese），2012，55（10）：3506－3515.

［17］ Schwarzbach C，Haber E.Finite element based inversion for time－harmonic electromagnetic problems.http：／／www.math.ubc.ca／～haber／Eldad＿Haber＿Web＿Page／Publications.html，2012［2013－03－21］.

［18］ Nocedal J，Wright S J.Numerical Optimization.New York：Springer－Verlag，1999.

［19］ Newman G A，Alumbaugh D L.Frequency－domain modelling of airborne electromagnetic responses using staggered finite differences.GeophysicalProspecting，1995，43（8）：1021－1042.

［20］ Egbert G D.A new stochastic process on the sphere：application to characterization of long－period global scale external sources.14thWorkshop on Electromagnetic Induction in the Earth and Moon，Brest，France，1994.

［21］ Siripunvaraporn W，Egbert G D.An efficient data－subspace inversion method for 2－D magnetotelluric data.Geophysics，65（3）：791－803.

［22］ Plessix R E， Mulder W A. Resistivity imaging with controlled－source electromagnetic data： Depth and data weighting.InverseProblems，2008，24：1－22.

［23］ Mackie R L，Rodi W，Watts M D，et al.3Dmagnetotelluric inversion for resource exploration.71stAnnual International Meeting，SEG，Expanded Abstracts，2001：1501－1504.

［24］ Mackie R L，Watts M D，Rodi W，et al.Joint 3Dinversion of marine CSEM and MT data.77thAnnual International Meeting，SEG，Expanded Abstracts，2007：574－578.