基于低通滤波的相敏检波算法改进与实现

于振南,刘倩,高秀晓,胡海涛

(1.中国石油集团测井有限公司测井技术研究院,北京 102206;2.中国石油长城钻探工程有限公司国际测井公司,北京 100200)

0 引 言

侧向测井仪器通过发射电极向地层发射不同频率的正弦信号,通过其变化情况反映地层电阻率,接收到的信号是多种频率的混合,夹杂着各种噪声。因此,精准地从其中提取出某一特定频率的正弦信号,进而计算它的幅值与相位变化(即检波),就成为真实客观地反映地层电阻率情况的决定因素。相敏检波技术常用来解决上述问题,但是不同的实现方法将直接影响最终的检波质量。早期采用模拟电路实现相敏检波,因为三极管的物理特性导致精度不高,且易受干扰[1]。随着数字信号处理理论及半导体技术的发展,基于DSP的数字相敏检波得到了广泛应用,使精度和抗干扰能力得到了极大提升。本文对当前已广泛应用的数字相敏检波方案进行改进,以得到更高的精度,使用MATLAB对改进前后2种方案进行仿真与比较。改进方案在侧向测井仪器中的实际应用效果表明,其在提高信号采集精度及抗干扰能力上具有优越性。

1 数字相敏检波原理

数字相敏检波的功能示意见图1。

图1 数字相敏检波的功能示意图

假设测量信号d(t)为

d(t)=Dcos (ωt-φ)=Dcosφcosωt+Dsinφsinωt

(1)

式中,D为被测信号幅度;ω为被测信号和参考信号的频率;φ为被测信号与参考信号之间的相位差。将Dcosφ记为DR,Dsinφ记为DX。它们分别为被测信号幅值的实部与虚部。

设

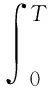
(2)

有

(3)

同理

(4)

(5)

被测信号幅值与相位为

(6)

这些数学推导为揭示了实现数字相敏算法的具体计算方法[2-3](见图2)。

图2 数字相敏检波算法的实现过程

2 数字相敏检波改进

上述实现方法,其实质是一个均值滤波的过程。可以向其中引入更有效的滤波算法,使最终的计算结果精度更高。通过对上面的数学推导进行改进,可以得到

(7)

同理

dR(t)=d(t)cosωt=

DRcos2ωt+DXsinωtcosωt=

(8)

式中,通过推导分离出直流与交流2个部分,可以使用低通滤波将其交流部分去掉,最终可得到直流部分,即被测信号幅值的实部与虚部。实现过程见图3。

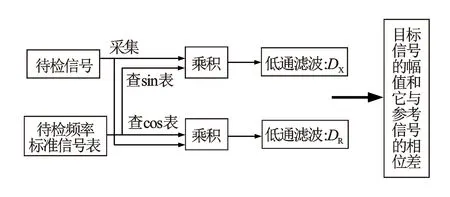
图3 使用低通滤波对数字相敏检波的改进

3 数字相敏检波的MATLAB仿真与对比

使用MATLAB软件对数字相敏检波算法改进前后进行仿真与对比,进而对其具体表现进行评价。改后算法中使用的低通滤波器由MATLAB的FDATool生成。采用四阶巴特沃兹低通滤波器,截止频率为5 Hz。改进前后数字相敏检波的计算结果对比见表1。表1中35、162Hz与288 Hz为3路正弦信号,其幅值分别为2.5、1.5 V与1.0 V。

表1为加入低通滤波之后的数字相敏检波在计算精度上普遍高于改进前。传统数字相敏检波的检波原理实质上是待检信号与参考信号之间的相关性计算。由于干扰信号的频率成分会对最终的计算结果产生贡献,因此,会影响检波的精度。而使用改进方案,在原理上将交直流进行了分离,在实现上使用低通滤波直接剔除交流分量,这将很大程度上提高检波的精度和抗干扰能力。

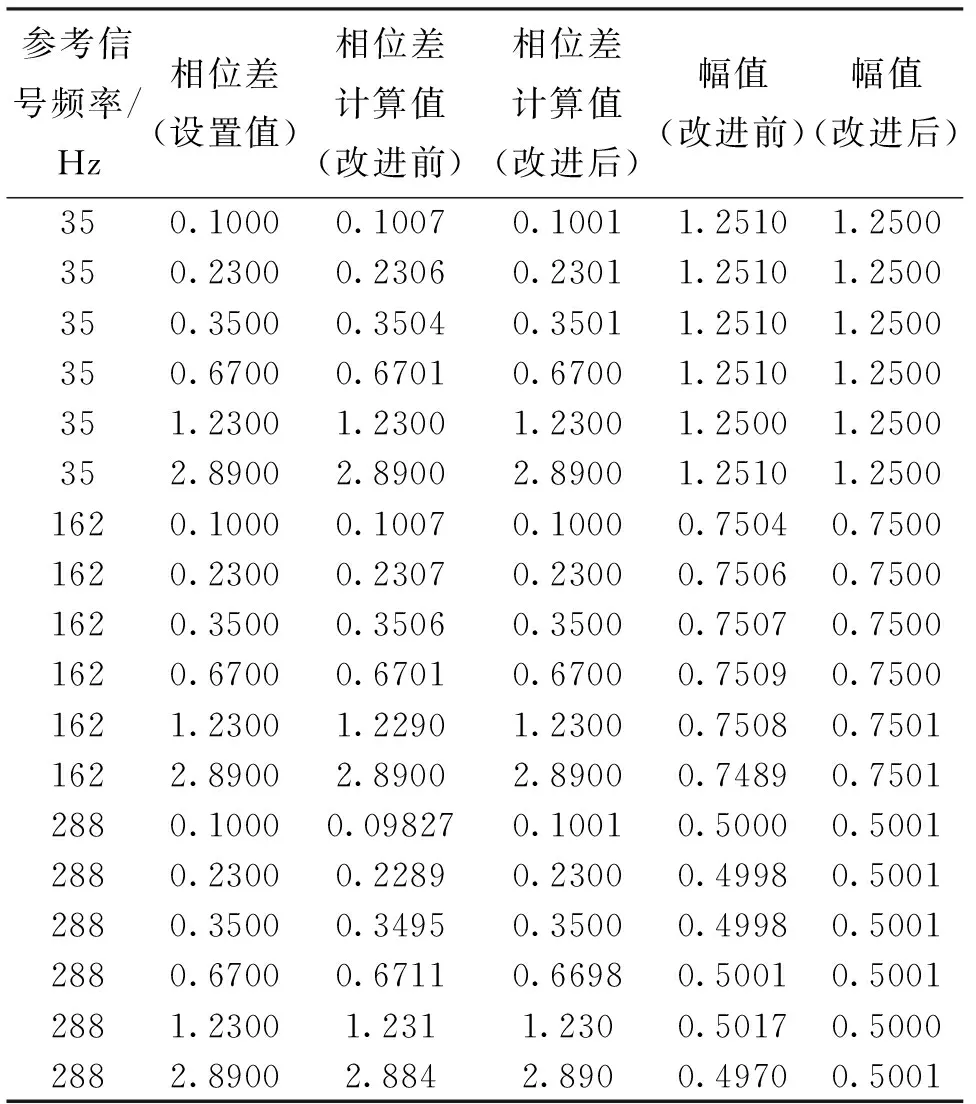
表1 改进前后数字相敏检波计算结果对比表

4 改进后数字相敏检波的实现

改进后的数字相敏检波加入了数字低通滤波的计算环节,并用C语言进行实现。数字低通滤波器的代码实现得益于MATLAB的FDATool所生成的参数。最终整体实现过程见图4。

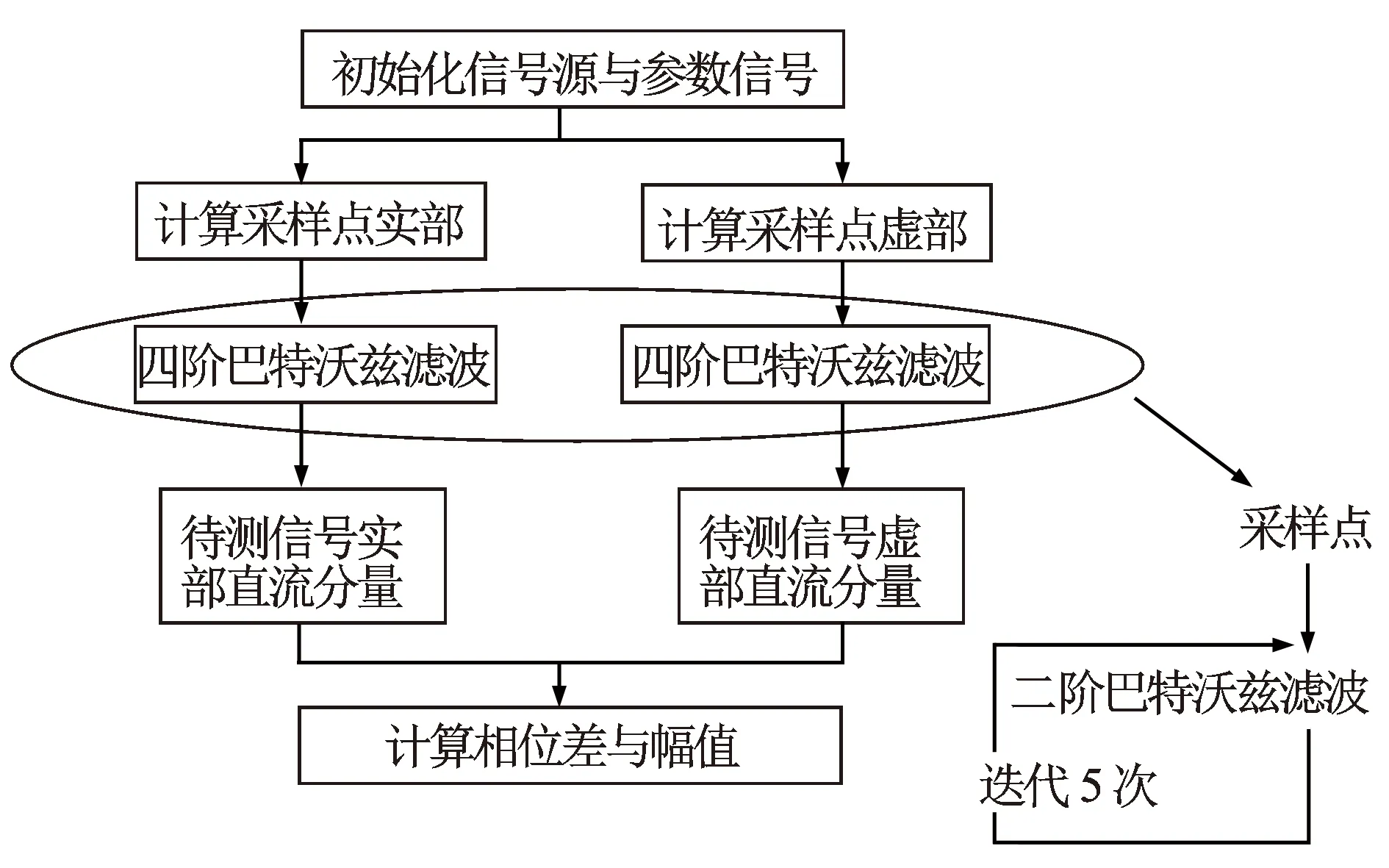
图4 改进后数字相敏检波的实现过程

图4中的二阶巴特沃兹滤波根据Direct Form I型IIR滤波差分方程[5-6]进行实现。经过5次迭代实现四阶低通滤波。改进前后数字相敏检波计算结果对比见表2。

表2 改进前后数字相敏检波C代码实现计算结果的对比

5 改进方案在侧向测井仪器中的应用

高分辨率侧向测井仪器采用了全数字化的设计方法,简化了电路,使得仪器可进一步短小化。信号采集与处理、滤波去干扰、聚焦与调节等工作均由DSP完成。仪器数字信号处理及电路总体框架见图5。

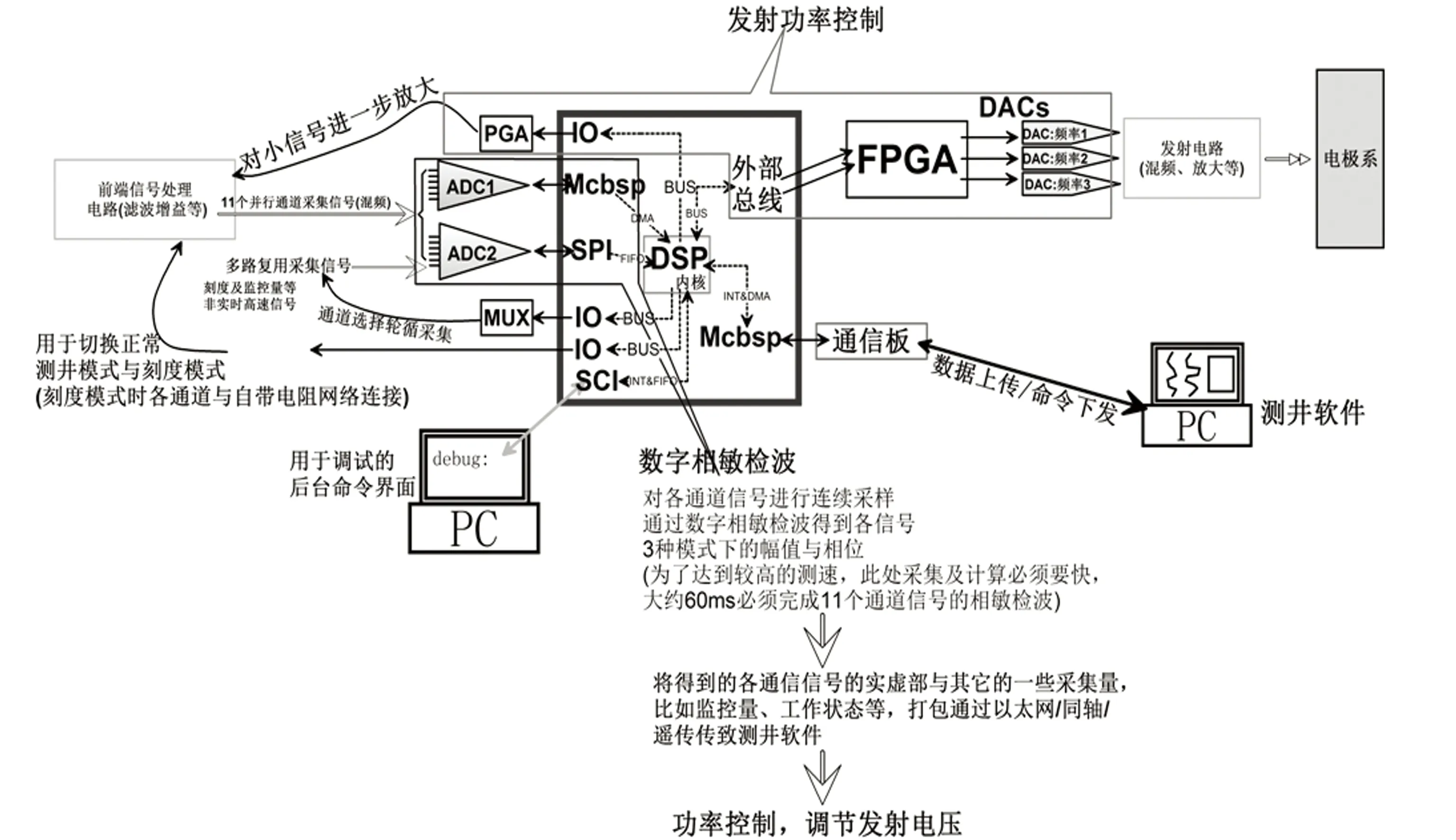
图5 仪器数字信号处理及电路总体示意图

实际测井过程中,信号的检波会遇到其他问题。在混合频率的信号中,当待检波的特性频率的信号量级较其他频率的信号量级较为悬殊,即信号的对比度或信噪比比较大时,传统相敏检波的精度将有较大损失,尤其是信号量级本身较小,如只有几mV或十几mV的时候,问题更为突出。基于低通滤波改进后的数字相敏检波,使这一问题得到了很大改善。实际应用证明,该检波算法得到的信号精度高、抗干扰能力强、信噪比高,对于采集蕴含在地层中的各种物理信息,尤其是微小信号,具有重要意义。

6 结束语

本文所提出的基于低通滤波的数字相敏检波算法达到了较好的检波效果。通过理论分析、仿真以及实际测井试验的结果表明,改进后的方案在检波精度、抗干扰能力等方面均得到了较大的提升。

将均值滤波改为低通滤波会增加计算量,但对于高计算能力的DSP满足改进算法的需求。本文所提出的方案已经应用在侧向测井仪器中,并取得了较好的效果,一定程度上解决了小信号的采集问题,使得最终的测井采集数据包含更丰富、更详细的地层物理信息。