基于随钻方位伽马测井的地层倾角自动识别

段友祥,闫亚男,孙歧峰,李洪强,2

(1.中国石油大学(华东)计算机与通信工程学院,山东 青岛 266580;2.中国石化集团胜利钻井工艺研究院,山东 东营 257000)

0 引 言

随钻方位伽马测井以常规自然伽马测井为基础,利用仪器不同方向上的多个伽马探测器进行测量,使伽马数据具有方位特性,可以根据方位特性反演得到地层构造情况,从而获得储层的边界、储层厚度和地层倾角等相关信息。在地质导向中可根据随钻方位伽马数据指导钻头准确入层,及时获得地层倾角,帮助分析地层结构,使井眼轨迹更准确地保持在目的层中,提高油气采收率。

地层倾角计算的2个必要参数分别为同一地层上不同2点之间的高度差和水平距离。目前,计算地层倾角主要有2种方案。①利用邻井信息,根据不同井钻遇同一地层时,2个钻点参数计算地层倾角。杨锦舟[1]应用邻井自然伽马建立先验模型结合人工经验进行了地质导向钻井;王谦等[2]根据邻井数据建立模型完成地层倾角计算和储层预测。但是,应用邻井信息计算倾角易受资源限制,邻井资料完整性影响着地层信息的准确性。②利用随钻方位伽马数据,根据方位数据计算地层倾角。侯爽[3]通过判断数据增量识别地层,但是不同的增量阈值会造成较大的效果差异;袁超[4]根据自然伽马图像进行了地层倾角及厚度计算,但需人工拾取计算的相关参数;McKinny K[5],Jiaxin Wang等[6]根据稳定区域均值识别边界并计算地层倾角,但是在实际钻井中数据很难稳定不变;Uzoh等[7]模拟不同地层条件下的方位伽马图像和曲线模型为人工识别服务;唐海全、肖红兵等[8]利用方位伽马曲线走势判断钻遇地层,但是无法计算地层倾角;Tyurin E等[9]在三维空间上计算地层真倾角,但仍需人工拾取地层特征。利用随钻方位伽马数据是计算地层倾角较为准确快速的方式,但是如何提取地层特征是目前难点之一。识别地层可以采用人工拾取、人机交互、计算机自动识别等方式。人工方式受经验影响较大,且速度慢;效率低;人机交互方式是人工拾取地层关键点,再由计算机计算,这种方式效率较高,但仍难以摆脱经验影响;计算机自动识别可以避免人为造成的影响和误差,而且效率更高,有利于快速作出正确的综合决策,提高开发效益,是目前的主要研究方向。

针对上述问题,本文以随钻方位伽马数据为基础,结合计算机图像处理等相关技术,对随钻方位伽马图像进行图像分割;通过地层边界曲线获取地层信息并完成地层倾角计算,以达到指导地质导向钻井的目的。该方法不仅实现了随钻方位伽马图像中的地层自动识别与倾角计算,而且满足了地质导向中的实际应用需求。

1 算法基本思想及流程

本文主要研究地层倾角自动识别,对随钻方位伽马数据进行归一化,并对归一化结果构造色阶直方图,综合考虑类内聚性和类间离散度,引入综合指标选取分割阈值;根据所选阈值对所有数据点进行阈值标记,自适应伽马数据测距,确定跟踪范围,按自定义跟踪顺序进行轮廓跟踪,获取地层边界;将哈夫变换正弦拟合与最小二乘拟合相结合,确定地层正弦公式;根据地层正弦参数计算地层倾角。算法流程见图1。

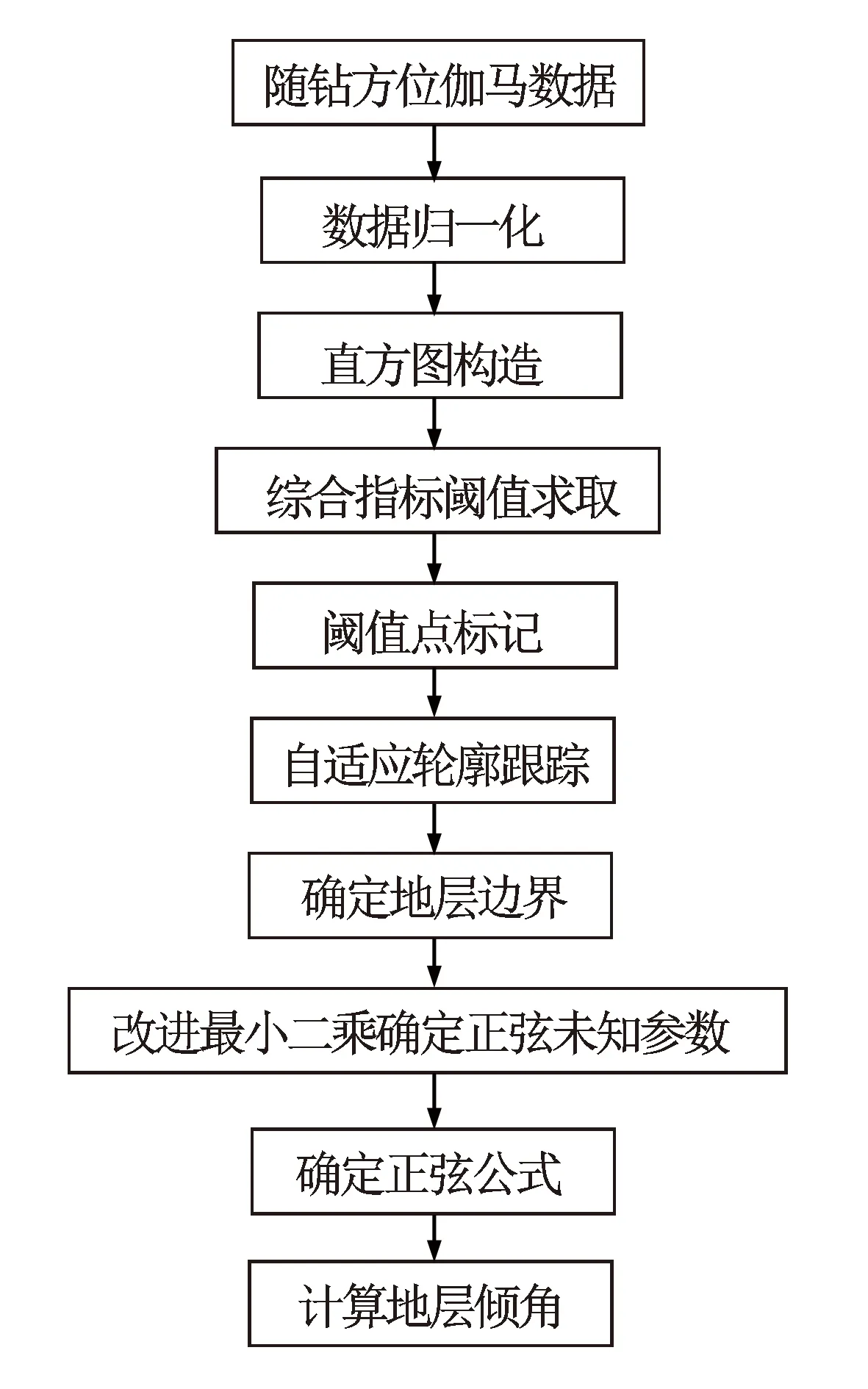
图1 算法流程图

2 伽马图像地层提取

2.1 综合指标阈值图像分割

识别地层就是要对伽马图像进行图像分割,即将伽马数据像素点分为不同的类,既要提高类内的相似度又要降低类间的相似度。本文首先对给定的随钻方位伽马数据进行归一化,再根据成像结果进行阈值分割。传统阈值分割采用图像灰度构造直方图,本文将伽马值映射为0～127级色阶,再转换为图像,但是在伽马数据→色阶→RGB值→灰度值的转化过程中,会丢失灰度值与伽马数据的正相关关系,所以本文将伽马数据映射后的色阶值作为数据输入,构造色阶直方图。

本文引用汪启伟[13]提出的综合指标,综合考虑衡量类内内聚性的熵和衡量类间离散度的类间差,选取阈值。熵值由式(1)计算,类间差由式(2)计算,综合指标由式(3)计算得到。

Hent(T)=

(1)

Hotsu(T)=pb(T)po(T)[mb(T)-mo(T)]2

(2)

(3)

式中,T为当前阈值;pb(T)、po(T)为2个类别所占总样本的比例;mb(T)、mo(T)为2个类别的类均值;went和wotsu分别为熵和类间差在计算综合指标时的权重,计算所有可选阈值下的综合指标,选取综合指标最大的值作为图像分割阈值。

2.2 自适应扩充邻域轮廓跟踪

图像分割阈值点即为表现伽马射线活动对比度平面上的点,确定阈值后,进行轮廓跟踪。轮廓跟踪通过顺序找出边缘点获取地层边界。具体过程如下

(1)列优先遍历图像中的所有数据点,对数据点(x,y),如果f(x,y)=value(value为阈值),则标记该点为阈值点;否则如果满足f(x,y)与f(x+1,y)位于阈值点两侧,则选取(x,y)与(x+1,y)中与阈值差距小的点标记为阈值点。

(2)建立二维链表BoundaryList作为边界链表。

(3)按照从上到下,从左到右的顺序找到一个未标记边的阈值点A,建立一个一维链表BList。

(4)若A不是噪声点或边界端点,在A点周围一定有一个阈值点,一般来讲应该按照左、左上、上、右上、右、右下、下、左下的顺序跟踪下一个阈值点。但是以阈值点作为边界有可能出现如图2所示情况,图2中红色点为阈值点,P1与P2同属一边界,但按照上述跟踪顺序,无法跟踪到P2。当出现P2、P3、P4的情况,从P2开始,按照上述顺序,会先跟踪到P4,导致丢失P3,但是针对实际情况,期望跟踪点依次为P2、P3、P4。根据随钻方位伽马数据的特性,只要边界连续,那么在图3中灰色区域内一定有阈值点。2点在纵向上相差行数由测距决定,可设定最小值,当测距较小时,2点纵向相差行数可能较大,根据实际情况,选取L内含有的数据行数为检测范围。

图2 轮廓跟踪图示 图3 伽马数据轮廓区域示例

本文分析了伽马数据中阈值点的分布属性,创建了适用于方位伽马数据的自适应轮廓跟踪算法,根据测距自动收缩或扩张跟踪范围。以先右后左、顺时针、近距离优先为原则建立了如图4所示跟踪顺序。

图4 自定义轮廓跟踪顺序

参数N由式(4)计算

N=4(L/step)+12

(4)

式中,Step为伽马数据测距;L为单边检测范围,本文中取0.2。按上述顺序跟踪下一个边界点,标记该点所属边,将该点加入到边界链表BList。

(5)以最新点为A点,重复步骤(4),直至跟踪不到阈值点,将单边链表BList加入到总边界链表BoundaryList。

(6)跟踪一条边界结束,查找下一条边界,重复步骤(3)到步骤(5)。

3 地层倾角计算

3.1 改进正弦拟合

经过轮廓跟踪获取到多条地层边界后,要对地层边界进行曲线拟合,确定每个地层平面在三维空间中的位置。钻孔与表现伽马射线活动对比度的平面相交,其形态见图5。在三维空间内投影在地层平面上显示为椭圆,在井壁的平面展开图上,观察到特征正弦响应,所以要将地层展开面上的地层边界线拟合为正弦曲线。

图5 地层与井筒相交示意图

井壁展开面上的正弦曲线表达式见式(5)

f(x)=Asin (ωx+φ)+y0

(5)

式中,A为振幅;ω为角速度;φ为初相位;y0为偏距,振幅是倾角计算中的关键参数。如图5所示,井壁展开面上是一个完整的正弦周期,即周期T是井壁展开面的宽度,角速度可由式(6)计算

(6)

在正弦公式中,只需要拟合3个参数:振幅A,初相位φ,偏距y0。

最小二乘拟合、迭代拟合[10]、基于哈夫变换的拟合[11-12]是测井数据处理中常用的3种正弦拟合算法,它们各有自己的优势和不足。最小二乘算法计算精度高,但是当范围过大时,计算量过大,计算速度慢;迭代拟合算法与最小二乘算法相比速度大幅提高,在单参数拟合时收敛效果较好,但在三参数拟合时难以保证收敛于最优值;哈夫变换算法速度最快,适合大量点中选择少数点拟合,是一个拾取和拟合相结合的过程,但是不适用于本文应用场景。为此,本文在研究分析3种拟合算法优缺点的基础上,根据伽马数据本身的特点,提出了一种适用于伽马数据的综合拟合算法。该算法过程如下:

(1)边界点排序。对轮廓跟踪中得到的二维链表BoundaryList,遍历每1条一维链表BList,对链表中的数据以x为关键字排序。

(2)确定初始偏移量。遍历链表BList中的点,对一个点(xa,ya)在BList中查询满足xb=xa+T/2的点(xb,yb),偏移y0根据式(7)计算

(7)

式(7)的原理是正弦本身的对称性。如图6所示,正弦上2点S1、S2横坐标相差半周期,2点中点Q一定在直线y=y0上。对所有计算结果,建立投票机制选择y0。

图6 正弦基线计算图示

(3)确定最小二乘参数范围。遍历链表BList中每一个点,得到y的最大值ymax、最小值ymin,以及y取最大值时对应的横坐标xmax,正弦公式中偏移量的遍历范围是[y0-(ymax-ymin)/6,y0+(ymax-ymin)/6],振幅的遍历范围是[0,(ymax-ymin)×2/3];由于正弦曲线本身的性质,初相位的遍历范围由式(8)确定

(8)

(4)计算残差。对3个参数的可取值自由组合,对每种组合(yi,Aj,φk)计算残差,残差Errorijk由式(9)计算

(9)

(5)确定参数。比较所有残差,残差最小的三参数取值即为该条边界的参数值。

(6)计算下一条边界。取BoundaryList中的下一条边界,重复步骤(2)到步骤(5),直至所有边界计算完毕。

3.2 倾角计算

地层倾角是地质导向中指导钻头行进的关键参数,根据正弦公式即可计算地层倾角。如图5所示,平面边界与钻孔相交的相对倾角可以用式(10)确定

(10)

式中,D为钻孔直径,计算中可认为等于钻头尺寸;H为正弦曲线在井壁展开面上的展布高度,等于正弦曲线振幅的2倍;根据Jiaxin Wang等[6]论文中的定义,DI为伽马图像的成像深度。Jiaxin Wang详细研究了不同地层倾角、地层密度、钻孔尺寸等环境对DI的影响,本文采用该思想,利用式(10),根据上文所得平面正弦参数计算地层倾角。

4 实验与分析

在随钻测井中,采用泥浆脉冲遥测方式将随钻方位伽马测井数据实时传输至地面,并对传输数据进行实时预处理与伽马成像。在实际钻井中,地质情况复杂,地层构造信息不精确。基于人工构造的地层模型,对测井响应进行正演模拟,可达到实测数据效果,而且可以提供准确的地层界面信息作对比参考。本文分析了前人研究的各种正演算法,最终采用邵才瑞[14]、Zhen Qin等[15]所用积分思想进行了随钻方位伽马数据模拟。

以随钻方位伽马模拟数据为基础,实验环境采用Visual Studio 2013和Open Scene Graph,实现了随钻方位伽马图像的地层自动识别与倾角计算。采用滑动窗口分析伽马图像,以最新更新数据为滑动窗口结束位置,使用本文算法处理滑动窗口内的图像数据。滑动窗口的窗长和滑动步长可根据实际情况设定,窗长设定过长,会导致数据量过多,降低分析效率;窗长设定过短,可能造成大倾角地层的倾角信息不完整,测得倾角存在误差;滑动步长设定过长可能会导致发现地层较晚,错过最佳控制钻头的时机;滑动步长设定过短会导致频繁分析伽马图像,降低分析效率,严重可能导致延误地层发现时机。设定更新井轨迹上一个采样点八方位数据的时间为一个单位时间,伽马数据的测距为0.1 m,八方位伽马数据横向内插为64个点数据,表1为该条件下不同窗长和滑动步长下的单位时间处理数据点数的比较。

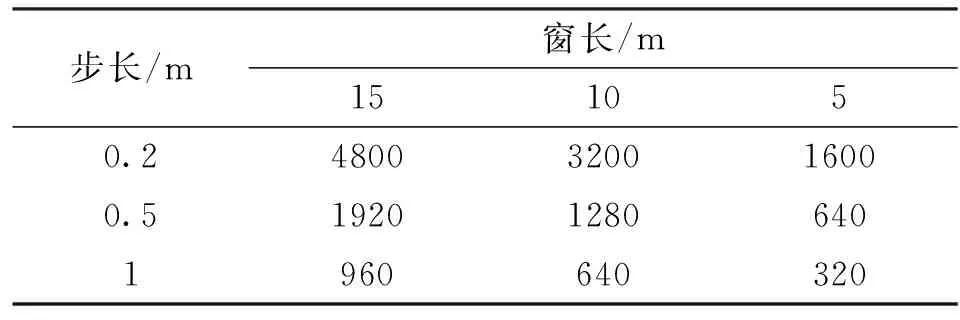
表1 不同滑动窗口处理数据量比较

正演模型中地层模型为砂岩和泥岩,地层模型相关参数见表2。K每秒平均发射光子数3.4/gs;Th每秒平均发射光子数1×104/gs;U每秒平均发射光子数2.8×104/gs[16-17]。

表2 正演模型相关地层参数

模拟4组数据作为实验数据,图7、图8、图9、图10分别为4组数据实验结果,表3为4组数据的识别结果与实际角度的对比及误差。

表3 本文算法地层倾角识别准确性

图7 第1组数据识别结果

图8 第2组数据识别结果

图9 第3组数据识别结果

图10 第4组数据识别结果

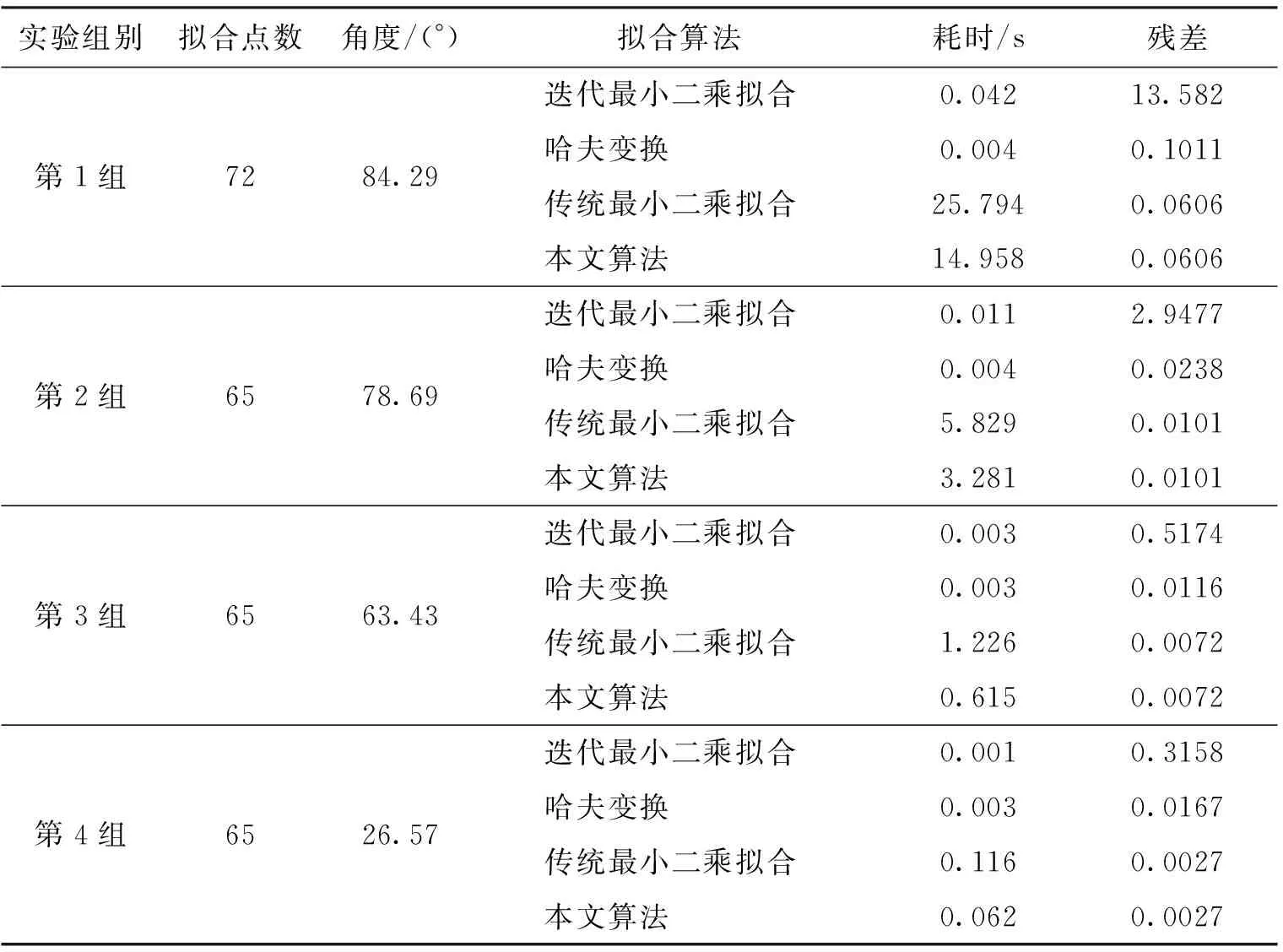
实验组别拟合点数角度/(°)拟合算法耗时/s残差第1组7284.29迭代最小二乘拟合0.04213.582哈夫变换0.0040.1011传统最小二乘拟合25.7940.0606本文算法14.9580.0606第2组6578.69迭代最小二乘拟合0.0112.9477哈夫变换0.0040.0238传统最小二乘拟合5.8290.0101本文算法3.2810.0101第3组6563.43迭代最小二乘拟合0.0030.5174哈夫变换0.0030.0116传统最小二乘拟合1.2260.0072本文算法0.6150.0072第4组6526.57迭代最小二乘拟合0.0010.3158哈夫变换0.0030.0167传统最小二乘拟合0.1160.0027本文算法0.0620.0027

本文所用正弦拟合算法,与迭代拟合和哈夫变换拟合相比残差更小;与传统最小二乘算法相比,耗时更少,表4为4种算法耗时及残差对比。

实验证明,本文所用图像分割、轮廓跟踪、正弦拟合算法取得了较好效果,可自动识别随钻方位伽马图像中的地层并计算地层倾角,且精确度较高。

5 结论

(1)针对利用随钻方位伽马数据获取地层倾角的问题,研究分析了各种计算方式的局限性,根据相关研究的成果与原理启发,结合计算机图像处理技术,建立了利用随钻伽马测井数据进行地层自动识别与倾角计算的方法,较好地解决了计算机自动进行地层倾角识别的问题。

(2)该方法采用综合指标计算分割阈值;提出了根据随钻方位伽马数据测距自定义跟踪顺序和扩充邻域进行轮廓跟踪;结合哈夫变换拟合思想改进拟合算法,缩小最小二乘计算范围,提高拟合速度,拟合地层分界线并计算地层倾角。

(3)本文方法针对不同的地层角度和地层构造均可有效识别地层并计算倾角,并且具有较高的正确率和运行效率。