功率因数调整的限制条件研究

颜秋容

(华中科技大学电气与电子工程学院，湖北武汉430074)

0 引言

功率因数PF(Power Factor)调整是电气专业“电路理论”课程的重要教学内容［1-4］。功率因数调整即通过在负载端并联电容来调整感性负载的功率因数，亦称无功补偿。教学中，计算此类问题可以采用无功功率平衡、电流补偿和导纳补偿三种思路，但这些思路均在忽略线路阻抗的前提下进行计算。《电路理论》教材中一般不强调线路阻抗的影响，从而让学生形成了通过在负载端并联电容总是可以将线路始端功率因数调整到任意要求值(包括PF=1)的深刻印象。

本文研究表明，考虑线路阻抗时，在线路末端负载上补偿电容，并非总能使始端功率因数调整到任意要求值。只有当负载阻抗Z=R+jX和线路阻抗Zl=Rl+jXl满足一定的条件时，始端功率因数才能任意调整，否则，在始端能够获得的最高功率因数小于1。本文的研究，指出了线路阻抗对提高始端功率因数的限制作用，同时，也想强调“电路理论”教学应该适当与工程实际相结合，这样有利于学生更为合理地应用理论去解决工程问题。

1 并联电容调整负载功率因数

在图1所示电路模型中，该线路阻抗为Zl=Rl+jXl，任意感性负载阻抗Z=R+jX，并联电容导纳为YC=jωC=jBC，Zm1和Zin2分别表示不包含和包含线路阻抗的等效阻抗。

图1 并联电容调整功率因数

通过选择BC的值，总可以将Zin1对应的功率因数调整到期望值。因为

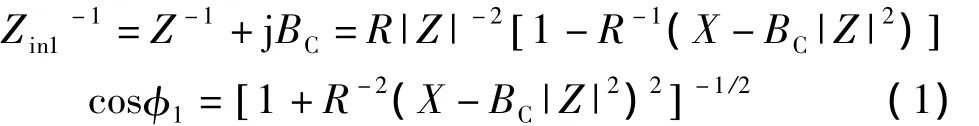
要使负载侧功率因数cosφ1可以在0～1之间任意变化，且为感性，只要X－BC|Z|2≥0，即要求

显然，对于任何负载阻抗Z，总可以选择满足BC≤X|Z|－2的电容。当BC=X|Z|－2时，cosφ1=1。

2 并联电容调整线路始端功率因数

考虑负载通过一定的线路接到电源，线路存在阻抗，通过选择的值，图1中的功率因数是否能在感性范围内任意调节且最大值为1呢?

2.1 线路始端的功率因数

线路始端阻抗为

化简后可得到

式中，函数g(BC)和f(BC)分别为

因此功率因数为

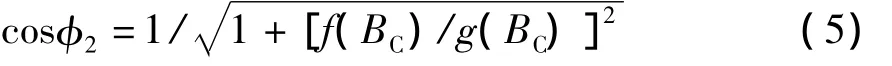
2.2 线路始端功率因数任意调整的条件

由式(3)可知g(BC)＞0，要使 cosφ2在感性范围内调节，则要f(BC)≥0，当f(BC)=0，cosφ2=1，f(BC)可以改写为关于BC的二项式，即

由式(4)可知，上式中

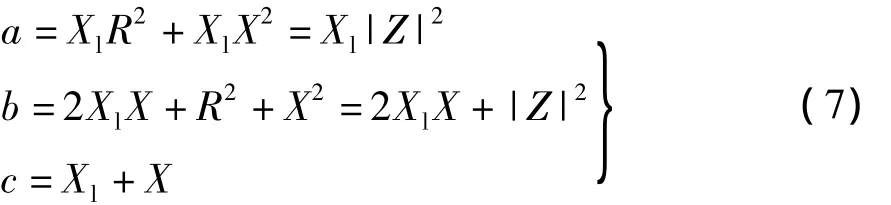
式中，a，b和c均为非负数，且a＞0，所以f(BC)曲线如图2所示。

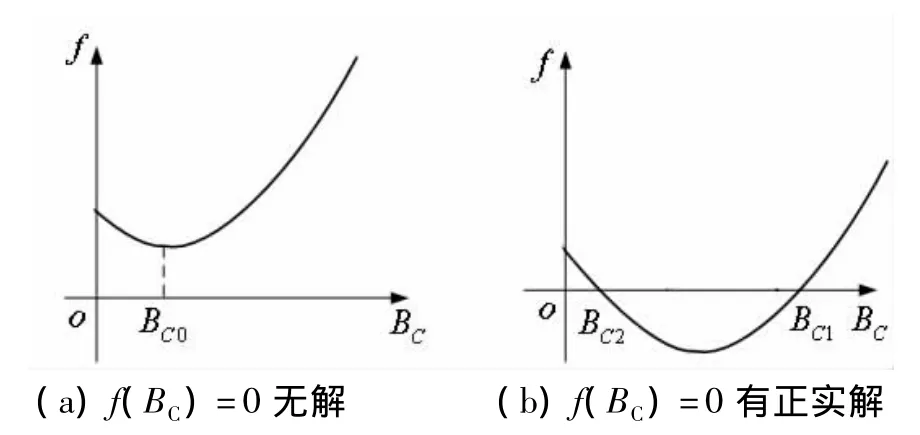
图2 f(BC)曲线的两种情况

若f(BC)曲线与横轴BC没有交点，如图2(a)所示，即f(BC)=0无解，表明cosφ2只能小于1。因此仅当f(BC)=0有正实数解时，才能通过选择BC获得cosφ2=1，即功率因数能在感性范围内任意调整，如图2(b)所示。

下面推导f(BC)=0有正实数解的条件。这里给出的f(BC)=0通解为

有实数解的条件为b2－4ac≥0。a，b和c均为非负数，显然b2－4ac≥0 成立时，必有BC1，2≥0，等号在c=Xl+X=0时成立。对应于Xl=X=0，此时不需要调整功率因数，表明功率因数需要调整的问题必有c＞0。只要f(BC)=0有实数解，则解一定为非零正实数。将a，b和c的表达式代入b2－4ac≥0中得到

上述分析表明：只有负载阻抗Z=R+jX和线路阻抗Zl=Rl+jXl满足式(9)时，才可以通过在负载上并联电容，使线路始端功率因数在小于等于1的范围内任意调整。在式(9)成立的条件下，假定BC1＞BC2，则当BC1=BC2时，cosφ2=1;BC1＜BC2时，cosφ2＜1(感性)。

2.3 线路始端功率因数的调整范围

不满足式(9)条件的问题，通过在负载上并联电容，线路始端存在一个小于1的极限功率因数cosφ2m＜1。由式(5)可知现在假设极限功率因数cosφ2m出现在BCm处，对应于h(BCm)=|f(BCm)/g(BCm)|的极小点。该点满足h'(BCm)=|f'g－g'f/g2|=0，即f'g－g'f=0。由式(3)和式(4)得

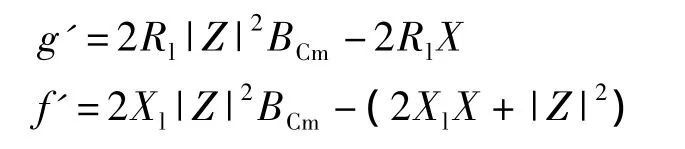
将f'g－g'f=0化简为Rl|Z|4BCm2+2(XlRRlX)|Z|2BCm+(2RlX2－Rl|Z|2－R|Z|2－2RXlX)=0，其解为

由于无论Rl和Xl取何值，必有BCm＞0。故上式取正号：

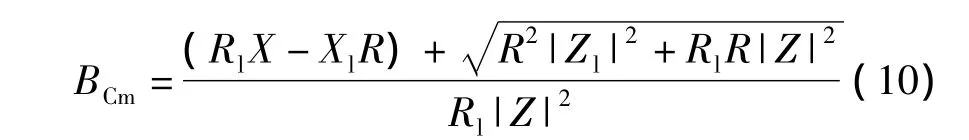
始端功率因数极大值为

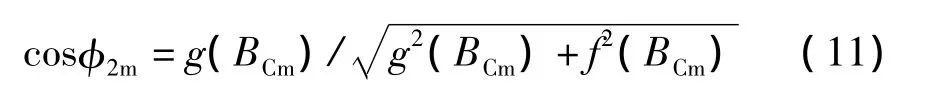
3 举例分析

假定负载阻抗Z=(1.45+j1.45)Ω，分析线路阻抗ZL取不同值时的补偿情况。

令Zl=Rl(1+jk)Ω，k=Xl/Rl，改变Rl、k的值，分析Zl对线路始端功率因cosφ2的影响，得到图3所示曲线。

图3(a)中，Rl=0.1Ω，k=1、3、6，计算得到|Z|2=4.205，2XlR=0.29、0.87、1.74，三种情况均满足式(9)，因此cosφ2最大值均为1。

图3(b)中，Rl=1Ω，k=1、3、6，计算得到|Z|2，=4.205，2XlR=2.9、8.7、17.4 。后二种情况不满足式(9)，对应的cosφ2最大值小于1。

结果表明，线路电阻增大及线路电抗和电阻比值增大，通过线路末端并联电容调整始端功率因数的范围变小。对于不满足式(9)的情况，Rl一定时，k=Xl/Rl越大，始端获得的最大功率因数越低。

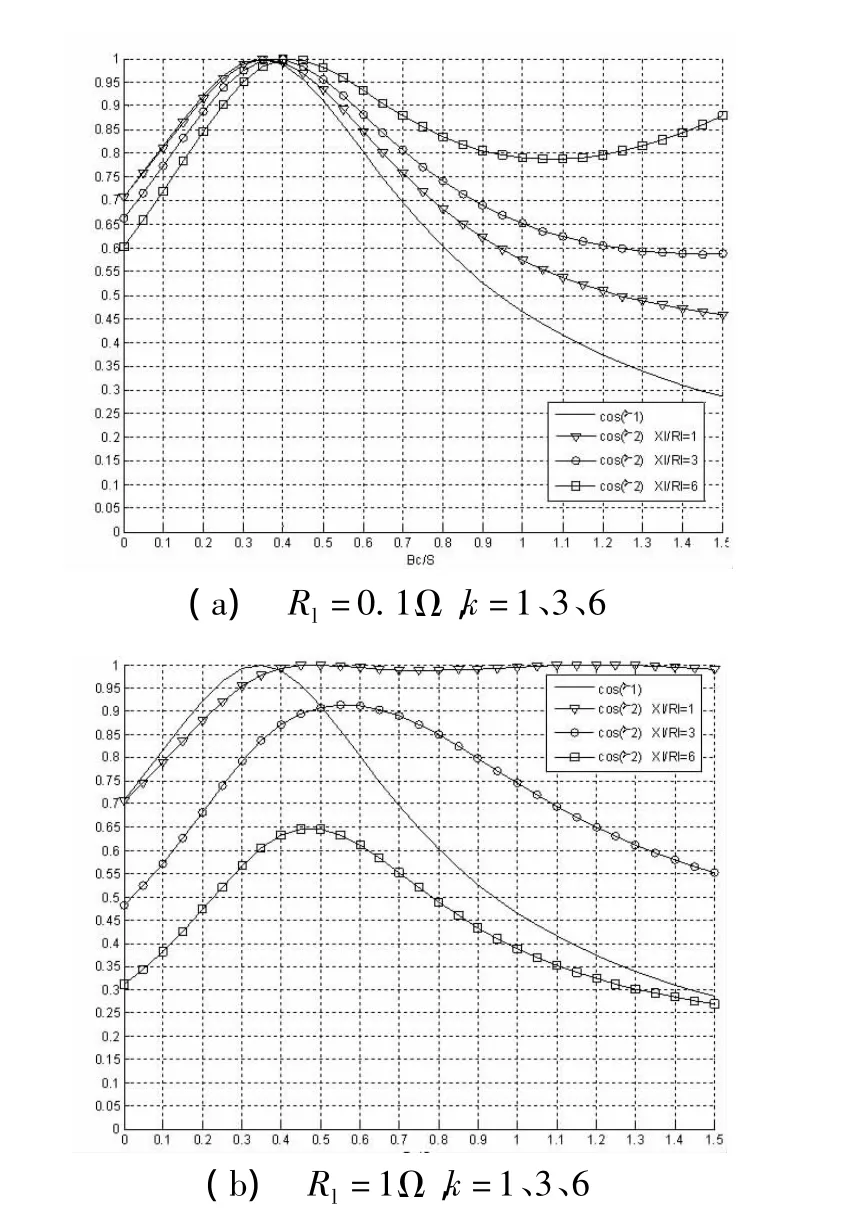
图3 不同Rl，k下的功率因数变化曲线

4 结语

本文推导出通过末端并联电容任意调整始端功率因数的限制条件，即|Z|2≥2XlR时，始端功率因数可以任意调整;对于不满足始端功率因数任意调整限制条件的问题，推导出始端所能获得的最大功率因数表达式，并通过实例进行了分析。结果表明，线路电阻增大以及线路电抗和电阻比值增大，通过末端并联电容调整始端功率因数的范围变小。对于不满足始端功率因数任意调整限制条件时，Rl一定，k=Xl/Rl越大，始端获得的最大功率因数越低。

［1］邱关源，罗先觉主编.电路(第四版)［M］.北京：高等教育出版社，1999年6月

［2］颜秋容，谭丹主编.电路理论［M］.北京：电子工业出版社，2009年11月

［3］于歆杰，朱桂萍，陆文娟.电路原理［M］.北京：清华大学出版社，2007年3月

［4］Charles K.Alexander，Matthew N.O.Sadiku.Fundamentals of Electric Circuits［M］.北京：清华大学出版社，2000