边值问题模拟与仿真实验研究

姜舒婷，卢斌先，崔 翔

(华北电力大学高电压与电磁兼容北京市重点实验室，北京102206)

0 引言

“工程电磁场”课程中的电磁场概念和理论抽象，利用单独的模拟实验不能很好的解决类似边值问题等重要内容，还必须结合数值仿真，才能使学生加深对电磁场概念的理解。本文基于笔者已发表的文献［1］内容，进一步开发了基于电路理论与电磁场静电比拟法的综合实验。

该实验不仅将“工程电磁场”边值问题数值仿真研究与模拟实验相结合，而且将电路的原理与电磁场原理相结合。实验中根据静电比拟法，先用示波器测量并计算各电极的单位长度的电导电容，再用电磁场数值分析软件ANSYS仿真计算各种电极单位长度电容，得到与模拟实验相同的结果即验证该数值仿真方法的正确性，使之可用于其他同类的复杂工程问题的计算。实验接着将数值仿真用于悬浮导体电位边值问题的计算。悬浮导体电位的计算有多种方法［2-4］，本文采用等效介质法和电路分析法，分别计算带电荷与不带电荷悬浮导体的电位。

该实验已在“电磁场数值计算”课程中对学生开放。文献［1］介绍的基础实验与本文新开发的综合实验共同形成了一个完整的边值问题实验群，对培养面向新时代电力工程的工程师有着重要意义。

1 边值问题实验群设计思路

“工程电磁场”边值问题的建立思路大致为：由基本实验定律引入场量的定义，进而推导出场量的性质，并由其定义出位函数的概念，位函数的泊松方程再结合边值条件即得所要求的边值问题。由此可见边值问题是各种场问题最终的硕果。据此，我们设计和开发了一套完整的边值问题实验群，如图1所示。通过组群的三个实验，一方面形成深化学习边值问题的系统过程，另一方面培养和提升了学生科学研究的基本素质，将科学研究中基础理论、数值仿真和模拟实验研究三要素传授给学生。从工程实践的角度看，这三个实验具有递进的关系。

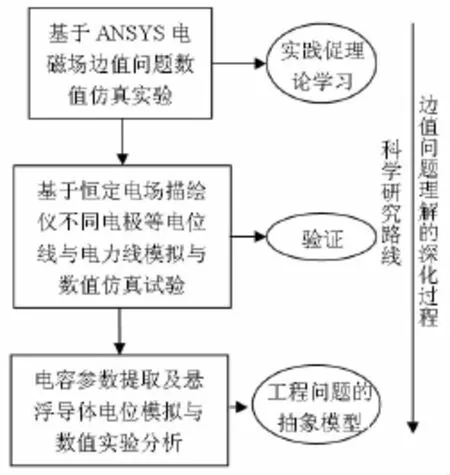
图1 边值问题实验群结构图

2 模拟电场描绘及测量计算极板电导

实验首先完成文献［1］介绍的恒定电场描绘仪实验，其接线如图2所示。其中AB连接电源，CB为测量端子。接着利用恒定电场描绘仪的电压源及示波器等进行测量并计算出各极板单位长度电导。由于实验回路中存在电容和电感，所以直流电压源与电压表均不能用于该实验。而用交流电压表也无法测出所需电压值，最终选择示波器测得其值。实验接线如图3所示。

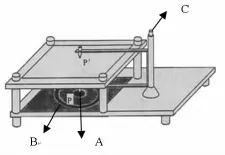
图2 电场描绘实验系线流

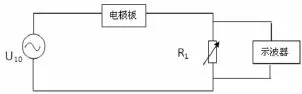
图3 测量计算单位长度电容图

第一步：按图3接线测量同轴圆柱面电极板的电导G0，并由下式求得该导电媒质(自来水)的电导率：

式中，b为外圆柱半径，a为内圆柱半径。

第二步：按图3接线测量各电极之间的电导，由静电比拟法得到

由上式可算得各电极之间单位长电容C0。

3 基于数值法仿真计算单位长度电容

基于电磁场有限元法，应用电磁场数值分析软件ANSYS计算各种电极结构的电位云图、电场线和等电位线，并计算各电极之间的单位长度电容C0。

数值计算实验要求根据等电位绘制过程中实际参数设置，分析电场强度矢量图和等电位线，计算电容参数。

表1中给出了五种导体结构的参数。

表1 单位长电容测量值与仿真计算值比较(10－10F)

表中给出的相对误差是以测量值为基准的百分比。由表1可知误差大部分在可接受范围内。其中聚焦电极误差较大，主要是因为该种电极结构复杂，用ANSYS数值仿真分析时建模过于简单所致。由此说明建模的重要性，这一问题作为学生应用ANSYS的扩展作业。通过该部分实验，学生学习了ANSYS软件的操作与应用，由可视化的场图直观地了解静电场，并通过后处理计算电极单位长度电容，得到的值与模拟测量结果基本相同，验证了仿真计算的正确性。

4 悬浮导体电位的分析

我们的进一步实验可以将数值仿真计算运用于小型工程问题的抽象模型中，如悬浮导体电位边值问题。带悬浮导体的同轴圆柱如图4所示，其等效电路图示于图5。求解方法可采用等效介质法和电路分析法。前者已在文献［1］中介绍过，现在重点讨论电路分析法的分析步骤。

(1)用ANSYS宏定义法计算出：

C10=1.54 ×10－9F，C20=2.04 ×10－9F，C12=5.68 ×10－10F。

图4 带悬浮导体的同轴圆柱

图5 电路图

(2)由图5的电路算出的U20即为悬浮导体的电位，其表达式为

其中，q=0C(当悬浮导体表面有电荷时，则其值为规定电荷量)，计算得U20=2.18V。可见它与等效介质法所得值相同。

5 结语

我们通过对恒定电场(静电场)等电位线绘制实验的改进，加入单位长度电容的测量与计算，模拟实验与数值仿真相互验证，以及引入悬浮导体电位的计算，完成一套完整的边值问题实验群。学生通过实验，不仅能更加深对理论知识的理解，而且能提高动手能力;加入的软件操作还能拓宽学生的知识面并提高计算能力，大大改善教学效果。

［1］姜舒婷，卢斌先.工程电磁场综合实验设计［J］.南京：电气与电子教学学报，2012，34(5)：78-80.

［2］郑勤红，解福瑶，钱双平等.用边界元法计算含有电位悬浮导体的静电场问题［J］.北京：电工电能新技术，1998，(2)

［3］崔翔.应用有限元方法计算含有电位悬浮导体的电场分布［J］.北京：华北电力学院学报，1995，22(2)：1-7.

［4］李旭，许懿.计算电位悬浮导体电场问题的有限元外推法［J］.北京：电气应用，2006，25(2)：19-21.