关于置换定理成立条件的讨论

田社平，张 峰，陈洪亮

(上海交通大学电子信息与电气工程学院，上海200240)

0 引言

置换定理(亦称替代定理)是“电路”课程的一个基本定理，它既是电路分析的工具，也是其它电路定理的理论基础，因此在教学中引起了广泛的讨论［1～6］。置换定理可表述为［7，8］：设一个具有惟一解的任意电路N，若已知第k条支路的电压和电流为uk、ik，则不论该支路是由什么元件组成的，总可以用电压为uS=uk的电压源或电流为iS=ik的电流源置换，而不影响电路未置换部分各支路电压和支路电流。从定理的表述可知，置换定理的成立条件是：电路置换前后具有惟一解。显然，置换前后电路具有惟一解是定理成立的充分条件，即只要该条件成立，置换定理的结论就成立。

笔者在置换定理的教学过程中，产生了这样的问题：定理表述中的电路解惟一性条件是否是置换定理成立的必要条件呢?对具有非惟一解的电路是否可以应用置换定理?

1 置换定理的实质

作为电路规律的概括与总结，置换定理表达了对电路中的某二端网络(或支路)进行置换的一种方法，该置换方法要求置换后不影响电路未置换部分各支路电压和支路电流。由于电路的解与电路对应的电路方程的解是一致的，因此，置换定理的成立条件也可表述为：电路置换前后未置换部分电路方程的解保持不变。显然，这一表述与电路惟一解的条件是有区别的。下面通过一具体电路来说明。

假设如图1(a)所示电路中的非线性电阻R1的伏安特性(非关联参考方向)为u1=(i－2)2V，而其非线性电阻R2的伏安特性(关联参考方向)为u2=-(i－2)2V。其中电流i的单位为安培(A)。

由图1(a)电路，不难得到二端网络N1和N2的端口特性分别为

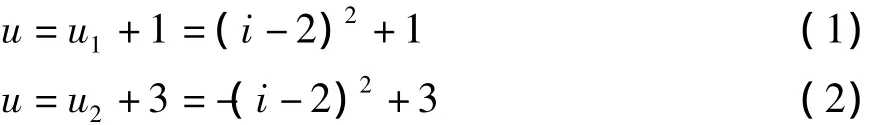
联立求解上述电路方程，可求得u=2V，i=1A或者u=2V，i=3A。可见，图1(a)电路是一个具有两个解的电路。

对图1(a)电路是否可应用置换定理呢?答案应该是肯定的。如图1(b)所示，用电压为2V的电压源置换N2，可列写出电路的KVL方程为2=(i－2)2+1，可解得i=1A或者i=3A。可见，这样的置换并没有改变未置换部分N1的电路解，因此这样的置换是合理、有效的。类似地，可用电压为2V的电压源置换N1，而不改变未置换部分N2的电路解。

由于端口电流具有两个不同的解，此时用电流源来置换N1或N2则是不合理的。例如，用电流为1A的电流源置换N2，如图1(c)所示，此时流经N1中非线性电阻R1的电流为i=1A，显然，这样的置换导致另一个电路解i=3A丢失掉了。

图1 置换定理的应用

我们可用电路伏安特性曲线更直观分析置换定理的应用。图2(a)画出N1和N2的端口伏安特性曲线。电压电流的参考方向见图1(a)，可见端口电压电流的解为点A(2V，3A)和点B(2V，1A)。如果用电压为2V的电压源置换N2，则电压源和N1的端口伏安特性曲线见图2(b)，可见端口电压电流的解仍然为点A和点B对应的解。如果用电流为1A的电流源置换N2，由图2(c)可知，端口电压电流的解仅为点B对应的解，无法得到点A对应的解。

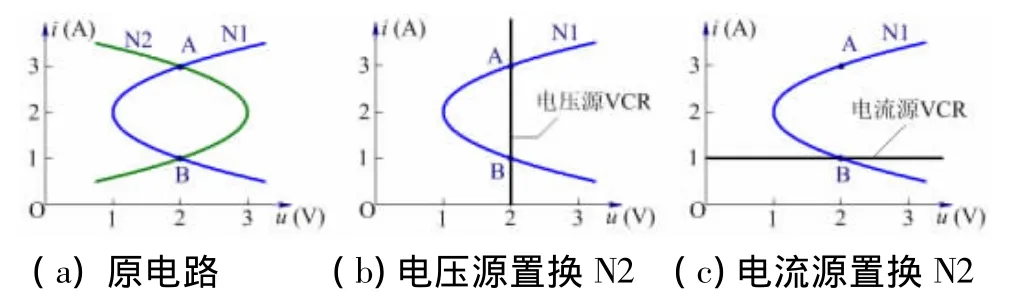
图2 置换定理图解示例

由上面分析可知，如果要求电路置换前后未置换部分电路方程的解保持不变，电路惟一解的条件不是必要条件，而是充分条件。

2 进一步的讨论

对于某些特定的具有无穷多解的电路，也可应用置换定理。如图3(a)所示电路，假设二端网络N1、N2的端口特性如图3(b)所示，则线段AB上的点对应的解都是图3(a)电路的解，因此图3(a)电路具有无穷多的解。由于端口电压的解为uk，因此二端网络N1或N2均可用电压为uk的电压源置换，用uk置换N2的电路如图4(a)所示，对应的端口特性曲线如图4(b)。可见，用电压源置换N2后，电路N1的解保持不变。

同样，假设二端网络N1和N2的端口特性如图3(c)所示，则线段AB上点对应的解都是图3(a)电路的解，因此图3(a)电路具有无穷多的解。由于端口电流的解为ik，因此二端网络N1或N2均可用电流为ik的电流源置换，用ik置换N2的电路如图4(c)所示，对应的端口特性曲线如图4(d)。显然，用电流源置换N2后，电路N1的解保持不变。

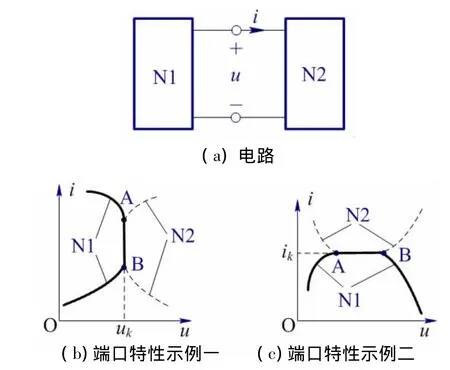
图3 电路有无穷多解时的端口特性

图4 电路有无穷多解时置换定理的应用

尽管当电路具有多解或无穷解时也有可能应用置换定理，但是这并不意味着教材中关于置换定理的叙述是错误的。事实上，文献［7］在说明置换定理时，指出“只要在置换后，网络仍有惟一解。”这就说明电路惟一解是置换定理应用的充分条件而不是必要条件。文献［9］在说明置换定理时，特别给出了一条注释：“对实际电路和大多数电路模型都具有惟一解，故本书不涉及非惟一解的情况。”这也说明了现行教材对置换定理的讨论仅限于电路具有惟一解的情况。

3 结语

本文针对电路教学中置换定理使用时要求电路具有惟一解的条件，说明了这一条件是充分而不是必要条件。当电路具有非惟一解时，也有可能应用置换定理。两种情况下的区别是：当电路具有惟一解时，被置换支路既可用电压源也可用电流源进行置换;而当电路具有非惟一解时，只有被置换支路的端口电压或端口电流的解为惟一值时，才能应用置换定理。此时，当端口电压解为惟一值时，被置换支路可用电压为该惟一值的电压源置换，而当端口电流解为惟一值时，被置换支路可用电流为该惟一值的电流源置换。显然，电路具有非惟一解时，被置换支路不可能既可用电压源也可用电流源进行置换。

值得指出的是，对于任意电路，即使其具有非惟一解，但在某一具体的时刻点，电路的解总是某个具体的确定值。此时如果已知被置换支路的电压或电流，则可由置换定理用一电压源或一电流源来置换该支路，而保持未置换部分电路的解不变。

由上讨论的结果，我们不妨将现有置换定理的表述修改为：“设一个任意电路N，若已知其第k条支路在某一时刻的电压和电流的具体值为uk和ik，则不论该支路是由什么元件组成的，总可以用电压值为uS=uk的电压源或电流值为iS=ik的电流源来置换该支路，而不影响电路未置换部分各支路电压和支路电流”。

经这样修改后的表述，可省去对电路要求有“惟一解”的条件，从而使得这样表述的置换定理更具有普遍性。在此提出此观点与同行商榷。

［1］张美玉，袁桂琴.替代定理的研究［J］.南京：电气电子教学学报，2000，22(4)：43～48

［2］汤放奇，谭志扬.也谈替代定理［J］.南京：电气电子教学学报，2001，23(4)：112～114

［3］张柏顺，刘泉.再谈替代定理［J］.南京：电气电子教学学报，2003，25(3)：101～103

［4］刘惠，白凤仙，董维杰等.电路课程中替代定理教学的探讨.南京：电气电子教学学报，2010，32(3)：27～29

［5］徐永谦等.关于《电路基本分析》中的替代定理问题的讨论.济南：科技创新导报.2008，No.4：147

［6］李光，永红，樊伟.电路中的等效与置换.济南：科技创新导报.2009，No.13：76

［7］李瀚荪.简明电路分析基础［M］.北京：高等教育出版社.2002

［8］陈洪亮，田社平，吴雪等.电路分析基础［M］.北京：清华大学出版社.2009

［9］陈希有.电路理论基础［M］.北京：高等教育出版社.2004