提高电动加载系统输出平滑的CMAC复合控制

杨 波 程 龙

（北京航空航天大学 自动化科学与电气工程学院，北京 100191）

电动加载系统用于在实验室条件下模拟飞行器在飞行过程中舵面所受的气动载荷，可以将经典的全实物实验转化为实验室条件下的半物理预测性实验，具有缩短研制周期、节约成本、提高可靠性和成功率的优点.

由于电动加载系统中不可避免地存在饱和、摩擦、间隙、弹性形变等非线性因素［1］及多余力矩的影响，传统控制方法的控制结果往往达不到理想效果，引入智能控制策略来代替传统控制方法成为了相关研究的重点.其中CMAC（Cerebellar Model Articulation Controller）控制策略因其学习速度快、能够克服局部最优问题、适用于在线学习且易于硬件实现而成为硬件平台算法的研究重点［2］，目前常用的是 CMAC和 PD（Proportional Derivative）的复合控制策略.

文献［3］将CMAC＋PD复合控制器应用于电动加载系统，仿真结果表明了CMAC＋PD复合控制在抑制多余力矩方面有很好的效果；文献［4－5］对基于CMAC＋PD复合控制的电动加载系统进行了稳定性和动态特性的分析，实验结果表明CMAC＋PD复合控制算法满足电动加载系统实时控制的要求，并且可以大幅提高电动加载系统的鲁棒性和稳态精度.

尽管CMAC＋PD复合控制策略在稳态精度和实时控制上有很好的表现，但与单独使用PID控制相比，CMAC＋PD复合控制策略在快速减小误差的同时会使输出波形的平滑性变差，在进行电动加载系统实验验证时，输出不平滑会导致电机频繁往复转动，使电机发生抖动，影响控制精度、加载频宽和电机的寿命.所以如何提高CMAC＋PD复合控制输出的平滑性就成为影响其进入实用阶段的关键问题.

国内外现阶段关于CMAC＋PD复合控制电动加载系统的研究大多停留于仿真阶段，没有实现对电机的实际控制，所以对于其控制电动加载系统平滑性方面的研究较少.由于CMAC算法的输出是由权值决定的，所以对权值进行平滑将直接影响输出结果.在CMAC权值平滑方面，文献［6－7］分别采用二次样条基函数和高斯基函数来替代传统CMAC的矩形基函数更新权值，以达到平滑输出的目的；文献［8］提出将每个权值向全部权值的均值接近，减少权值间差异的方法进行平滑.尽管这些算法都有助于提高CMAC的输出平滑性，但这些算法本质上都是在权值更新后再对权值进行平滑，平滑效果有限.

本文通过分析CMAC算法权值调整指标与输出平滑性的关系，提出了提高CMAC输出平滑性的改进算法，该算法在权值调整指标中同时考虑误差和相邻权值间差异的影响，推导出一个新的权值更新公式，在权值更新时直接达到减小误差和增进平滑性的目的.通过仿真和实验证明，这种新算法对于提高电动加载系统控制精度和平滑性有很好的效果.

1 CMAC＋PD复合控制原理

CMAC的结构如图1所示，它由网络输入、概念映射、物理映射和网络输出4个基本部分组成.图1中，输入向量X中的每一个点都与概念存储空间P中的C个存储单元相对应，然后这C个存储单元又与物理映射w的C个单元对应，而神经网络的输出Y就是这C个物理存储单元中权值之和.

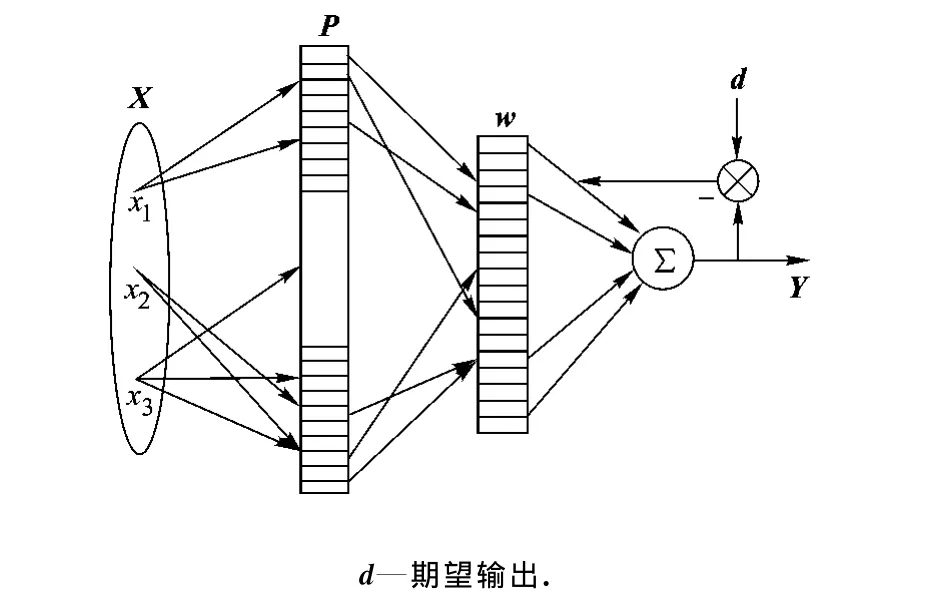
图1 CMAC结构图

基于CMAC＋PD复合控制的电动加载系统控制器结构如图2所示，其中CMAC以误差作为训练信号来调整CMAC的权值，实现前馈控制，确保系统的响应速度，减少超调量.常规PD算法实现反馈控制，以保证系统的稳定性.

图2 CMAC＋PD复合控制器结构图

2 复合控制输出平滑性问题分析

目前CMAC＋PD复合控制的研究重点在稳态精度、稳定性和多余力矩抑制方面，在控制电动加载系统时的平滑性方面研究很少.但CMAC＋PD复合控制法与普通PID控制法相比，存在输出不平滑的问题，图3、图4是CMAC＋PD复合控制算法（简称CMAC＋PD算法）和普通PID控制电动加载系统在0.5Hz下跟踪幅值为5N·m的正弦信号时的测试结果.可以发现单独使用PID控制电动加载系统时尽管稳态精度不高，但输出波形较为平滑，而使用CMAC＋PD算法时，尽管稳态精度较好，但输出波形却不平滑，波形有很大波动.这种波动在仿真时不明显，但是实际控制电机时，这种输出的增减趋势的频繁变化会导致电机频繁往复而产生抖动，这种抖动对控制精度、加载频宽和电机的寿命都有不利的影响.因此有必要对CMAC＋PD算法进行改进以保持较好的稳态精度的同时提高输出的平滑性.

图3 PID在0.5Hz下测试结果

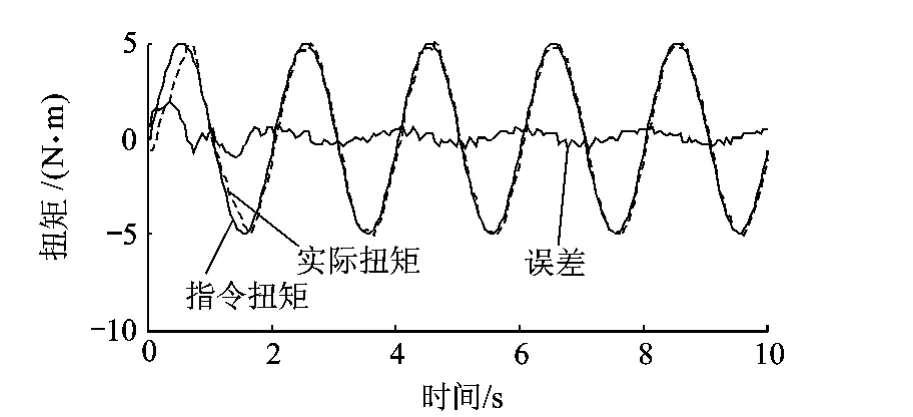
图4 CMAC＋PD算法在0.5Hz下测试结果

3 改进的CMAC算法及仿真分析

3.1 改进的CMAC算法

由传统CMAC计算原理可知，每一个输出都与物理存储空间w中的C个权值关联，这些权值的和构成了输出

式中，行向量a中有C个值为1，其余为0，用于表示输出yi与w的关联关系.定义Y为输出向量，A为对应的选择矩阵，则Y可以表示成

由式（2），可以得到误差向量：

传统的CMAC权值调整公式为

式中，R为单位矩阵.

权值更新公式为

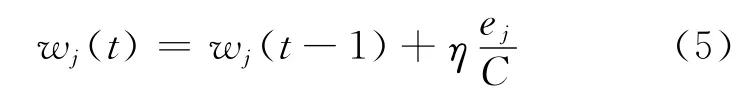
式中，η为学习率.

传统的CMAC权值更新算法仅仅根据误差来更新权值，由于CMAC相近的输入激发相邻的权值的性质，相邻权值间的差异也会随误差变大，导致由式（1）计算的输出的差距变大，使输出更加不平滑，进而影响PD的输出使CMAC＋PD算法的不平滑现象加剧.

当CMAC应用于仿真时，这种输出的变化虽然会导致输出波形不平滑，但有利于快速的减小误差，取得更好的稳态精度.但是当CMAC应用于实验控制加载电机时，系统中的非线性因素会加剧输出的频繁变化，直接导致电机抖动，造成误差加大甚至有可能损伤电机.因此针对电动加载系统实验的实际情况，需要对CMAC的权值更新方法进行修改，以增加输出的平滑性.

由于在满足误差减小的同时，一定存在一组变化最小即代价最小的权值，使输出满足误差最小且输出平滑需要.基于这个思想，现在使用新的权值调整式（6）来考虑新的权值更新方法，该公式同时考虑了误差和临近权值差异，通过调整权值更新公式以获得式（6）的最小值，可以使CMAC算法在获得更小误差的同时减小相邻权值间的差异，以获得更平滑的输出.

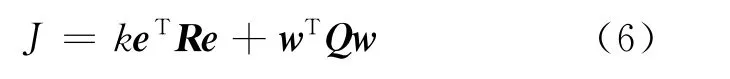
其中，k为误差在权值调整指标中的比重系数；Q为一个对称的三对角矩阵：

wTQw是相邻权值的差的平方和：

为了找到权值的最优解，对J关于w求偏导，并使偏导为0，有

式（9）可化简为

解得

由于电动加载系统使用单输入单输出的CMAC算法，因此式（11）可以进一步简化为如下形式：

新权值更新公式（12）同时考虑了减小误差和增加平滑性，替代了原来的增量式公式.

3.2 改进的CMAC算法仿真及结果分析

以文献［9］中的电动加载系统模型为基础进行仿真，采用如图2所示的CMAC＋PD复合控制结构.其中PD参数设定为KP＝1，KD＝0.05；CMAC的参数设定为：量化参数N＝100，C＝15，η＝0.2，k＝6.

现在对传统CMAC＋PD算法和本文的改进算法进行仿真比较，加载指令设置为

式中，ts为采样周期1ms；n为仿真步长.并加入多余力矩干扰信号：

仿真结果的误差比较如图5所示.

图5 仿真结果的误差比较

从图5可以看出，传统CMAC＋PD算法在仿真过程中初始误差幅值大约0.5N·m，但是随着仿真的进行误差增大，且波形不够平滑.使用改进CMAC＋PD算法误差较小，稳态误差幅值大约0.44N·m，且波形平滑.

仿真结果表明改进CMAC＋PD算法在控制电动加载系统的稳态精度和平滑性上都有很大改进.

4 改进CMAC算法实验验证及分析

本文利用实验室的电动加载系统来验证改进CMAC＋PD算法的有效性，该系统由力矩电机、DSPF28335、扭矩传感器、驱动器、调理电路和上位机组成，系统的总体结构如图6所示.

图6 舵面电动加载系统结构图

实验测试的参数与仿真参数保持一致，加载指令幅值为5N·m的正弦信号，频率f分别选择1.0，1.5，2.0Hz.传统CMAC＋PD算法和改进CMAC＋PD算法的实验测试数据结果如图7～图12所示.

图7 传统CMAC＋PD算法在1Hz频率下加载结果

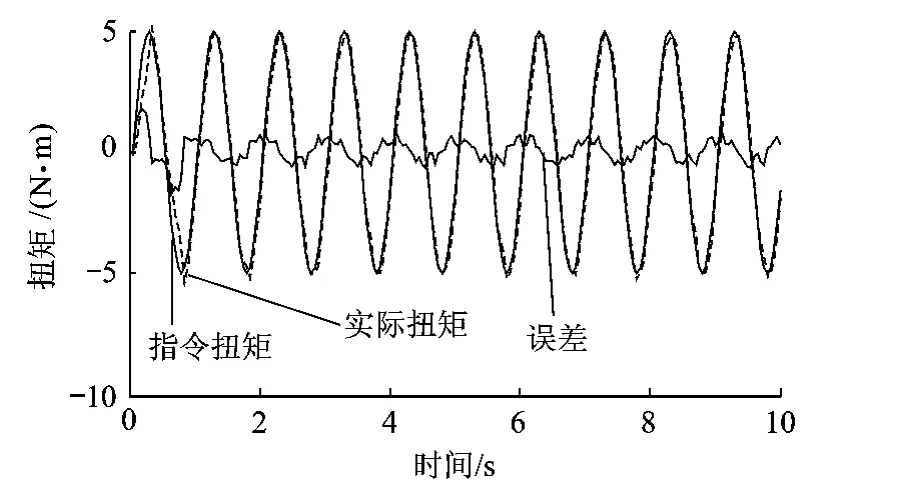
图8 改进CMAC＋PD算法在1Hz频率下加载结果

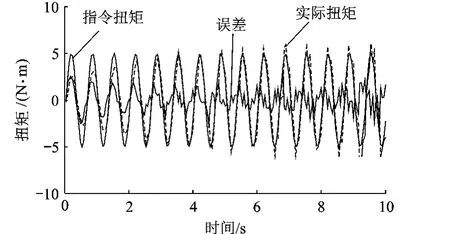
图9 传统CMAC＋PD算法在1.5Hz频率下加载结果

10 改进CMAC＋PD算法在1.5Hz频率下加载结果

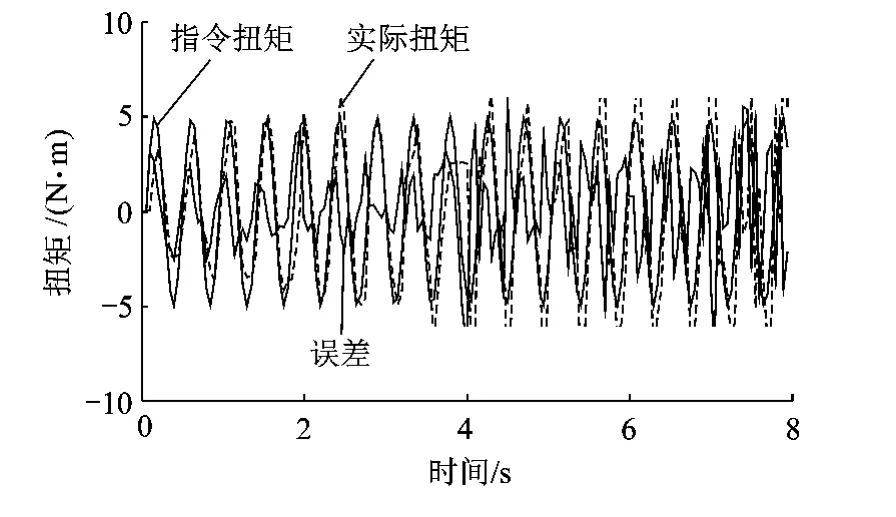
图11 传统CMAC＋PD算法在2Hz频率下加载结果

改进CMAC＋PD 算法在1.0，1.5，2.0Hz频率下5s后的最大误差幅值为0.93，1.11，1.57 N·m，而传统CMAC＋PD算法在1.0Hz频率下5s后的最大误差幅值为1.19N·m，在1.5，2.0Hz频率下5s时已有发散趋势.实验结果表明改进CMAC＋PD算法与传统CMAC＋PD算法相比有更好的稳态精度和稳定性，且从误差波形可以看出，改进CMAC＋PD算法的输出波形更加平滑.

图12 改进CMAC＋PD算法在2Hz频率下加载结果

对加载平台施加幅值为5N·m，频率为1Hz的60s的正弦信号，并通过在加载过程中扳动连接轴来施加位置干扰，加载结果的误差如图13所示.施加的干扰分别为13s及30s附近的两次小幅度干扰和45s及50s附近的两次大幅度干扰.可以观察到在干扰移除后控制策略能很快恢复稳定状态，具有很好的鲁棒性和抗干扰性.

图13 改进CMAC＋PD算法在干扰下加载的误差结果

5 结 论

本文对传统CMAC＋PD复合控制应用于电动加载系统时输出不平滑的影响因素和危害进行了分析，提出了一种同时满足减小误差和输出平滑性要求的改进CMAC＋PD复合控制算法.该算法通过新的权值调整指标推导出了新的权值更新公式，在权值更新时直接达到减小误差和增进平滑性的目的.仿真和实验结果表明，与传统的CMAC＋PD复合控制算法相比，该改进CMAC＋PD复合控制算法能有效提高控制电动加载系统时的稳态精度和输出平滑性，并且具有良好的鲁棒性和抗干扰能力，更适用于电动加载系统的控制.

（References）

［1］王瑞，陈松林.电动负载模拟器输出力矩的影响因素分析［J］.测试技术学报，2011，25（1）：47－51

Wang Rui，Chen Songlin.Analysis of influence factors on output moment of electrical lord simulator［J］.Journal of Test and Measurement Technology，2011，25（1）：47－51（in Chinese）

［2］李守奇.基于CMAC与PID的无刷直流电机复合控制算法仿真［J］.科教新报，2011（3）：254－255

Li Shouqi.Composite control of brushless DC motor based on CMAC and PID algorithm simulation［J］.Science and Education，2011（3）：254－255（in Chinese）

［3］杨波，王俊奎.无人机舵面负载模拟系统的小脑模型控制［J］.北京航空航天大学学报，2009，35（11）：1361－1365

Yang Bo，Wang Junkui.CMAC neural network for the rudder dynamic load simulator of unmanned aerial vehicles［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35（11）：1361－1365（in Chinese）

［4］王刚，李建府，朱荣刚.CMAC改进算法在电动负载模拟器的应用［J］.电光与控制，2011，18（4）：72－76

Wang Gang，Li Jianfu，Zhu Ronggang.Application of an improved arithmetic based on CMAC in electrical load simulator［J］.Electronics Optics and Control，2011，18（4）：72－76（in Chinese）

［5］杨波，黄耀达，台钰莹.基于BOWA小脑模型的高精度稳定电动加载系统［J］.航空学报，2012，33（4）：734－743

Yang Bo，Huang Yaoda，Tai Yuying.High precision and stable electric loading system based on BOWA-CMAC［J］.Acta Aeronautica et Astronautica Sinica，2012，33（4）：734－743（in Chinese）

［6］Wang S Y，Tseng C L，Yeh C C.Adaptive supervisory Gaussian-cerebellar model articulation controller for direct torque control induction motor drive［J］.Electric Power Applications，2011，5（3）：295－306

［7］Fu Yanli，Li Shijing，Xiao Yunshi.Study on new neural network adaptive control of industrial manipulators based on desired compensation［C］／／Song Jian.7th World Congress on Intelligent Control and Automation.Chengdu：IEEE，2008：6983－6987

［8］Ge Yingqi，Luo Xiaoping，Du Pengying.A new improved CMAC neural network［C］／／Wang Fuli.22nd Chinese Control and Decision Conference.Xuzhou：IEEE，2010：3271－3274

［9］杨波，王俊奎.基于改进的CMAC的电动加载系统复合控制［J］.航空学报，2008，29（5）：1314－1318

Yang Bo，Wang Junkui.Hybrid control based on improved CMAC for motor-driven loading system［J］.Acta Aeronautica et Astronautica Sinica，2008，29（5）：1314－1318（in Chinese）