通用直升机雷达散射特性及RCS减缩

包晓翔 张云飞 杜晓松

（北京航空航天大学 航空科学与工程学院，北京 100191）

通用直升机执行战术人员运输、电子战、空中救援、布雷、反潜、反舰、垂直补给等任务，在现代战争中越来越重要.现代电子探测技术和导弹技术的发展，对军用直升机生存构成严重威胁.为了提高直升机生存力和作战能力，“隐身”已成为现代直升机重要战术指标之一［1］.雷达隐身是直升机隐身技术的重要内容，开展直升机雷达散射特性分析和雷达散射截面 RCS（Redar Cross Sec-tion）减缩研究有重要的理论意义和实际价值.

由于保密等原因，目前国外对于飞行器（特别是直升机）外形隐身研究公开发表的文章相对较少，但美国等西方国家从20世纪70年代就投入大量人力物力开展飞行器雷达散射截面的研究，在直升机隐身方面取得不少成果，典型的是美国的RAH-66“科曼奇”隐身武装直升机.2011年5月，美国在巴基斯坦执行抓捕本·拉登行动中，意外坠毁的新型直升机的残骸具有独特的外形，据分析认为是“黑鹰”直升机的隐身化改形.

国内积极开展了对直升机雷达散射特性的研究.苏东林等［2］做了武装直升机雷达散射截面估算方法研究；叶少波［3］建立了武装直升机隐身外形优化的计算机辅助设计软件系统；蒋相闻等［4］基于面元边缘法做了某型武装直升机RCS计算分析.但缺乏对通用直升机的隐身设计研究.

在电磁学算法［5］中，精确算法，如时域有限差分法（FDTD）、矩量法（MOM）、快速多级子算法（FMM）等数值计算方法具有较高计算精度，但涉及到大型目标、高频波段时，其对计算机硬件要求高，运算时间长，计算效率低.改进的多层快速多级子算法［6］虽然提高了算法的效率，但仍然对计算机硬件要求较高，不适用于工程快速估算.高频近似算法对上述目标的计算效率高，虽然精度比精确算法低，但能满足工程估算要求.

本文就通用直升机的静态雷达散射特性及RCS减缩进行研究，至于旋翼和尾桨的动态RCS可结合频域分析，将另行研究.首先，建立常规通用直升机几何外形模型；采用物理光学法（PO）和等效电磁流法（MEC）作为数值计算方法［7－8］，并通过实验测试验证了算法的有效性；然后计算分析了常规通用直升机的雷达散射特性；最后，借鉴固定翼飞行器隐身设计技术，进行通用直升机的RCS减缩研究.

1 几何建模与RCS计算

1.1 模型建立

在三维CAD软件CATIA中，采用NURBS曲面［9－10］，进行常规通用直升机造型，构建几何外形模型（见图1），其主要技术数据［11］见表1.考虑到直升机进气口一般带有过滤网罩，其格栅间距比电磁波波长小，电磁波将无法进入进气道而反射出去.因此在进气口处，利用封闭曲面等效代替过滤网罩.尾喷口采用短路终端［12］处理，即，使用与叶片终端同径的圆板来封闭尾喷口.

图1 常规通用直升机几何外形造型

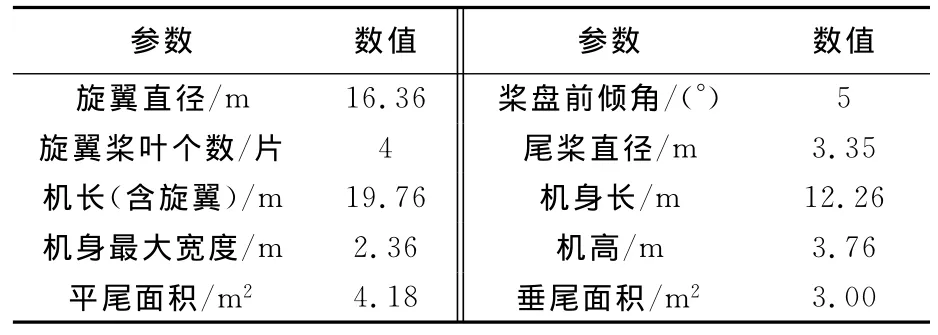
表1 通用直升机主要技术数据

在CATIA中划分直升机几何外形的三角形网格（见图2）.为保证网格形状与几何模型的误差小于波长的1／16，设置网格与几何模型最大偏离高度为1mm，并在模型曲率较大的地方采用了加密网格.输出包含942 201个三角形面元，471 094个节点，1 413 293个边缘的拓扑结构数据文件.

图2 常规通用直升机几何外形网格划分

1.2 RCS计算方法

采用物理光学法（PO）计算面元散射，结合等效电磁流法（MEC）计算边缘绕射.

RCS平方根物理光学（PO）表达式为

式中，S为目标受到雷达照射部分的表面；r为局部原点到表面单元dS的矢量；为物体表面的单位法矢量；r表示接受装置电极化方向单位矢量.

等效电磁流（MEC）计算边缘散射表达式为

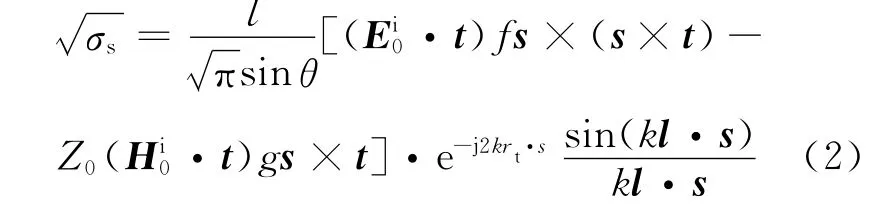
式中，t为强制边缘单位矢量方向；θ为入射线i与t的夹角；s为散射方向单位矢量，其他参数见文献［13］.

在RCS计算前，需将输出的网格数据进行消隐遮挡处理，阴影区和被遮挡部件的面元和边缘不参与RCS计算.

总目标RCS是所有n个面元和m个边缘的RCS之和：

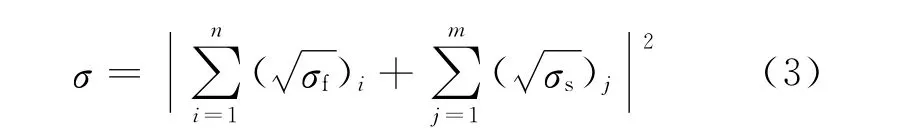
1.3 RCS计算方法验证

为了验证本文RCS数值计算方法的有效性，利用翼展为1m的某飞翼模型（见图3）作为算例，与微波暗室的实验测试数据进行比较.计算条件为：雷达工作频率f＝10GHz，俯仰角和滚转角均为0°，HH极化，结果见图4.

图3 用于算例验证的某飞翼模型

图4 RCS数值计算与实验测试对比

从图4的对比结果可见，RCS计算值与测试值总体吻合较好.由于模型结构采用木材制作并在表面贴铝箔，工艺较粗糙，实验模型与数值模型有些差别（见图3），另外测试时模型姿态摆放有误差，都会导致某些角度RCS计算值与测试值有略微的差异，但对RCS总体趋势和数值水平影响不大.表明本文RCS数值算法是有效的，可以用来计算评估直升机雷达散射特性.

2 常规通用直升机的RCS特性

计算分析常规通用直升机雷达散射特性：方位特性、极化特性以及频率特性.

由于直升机在空中时旋翼处于旋转状态，其RCS随时间呈周期性变化.求静态RCS时，考虑到最不利状态，将桨叶前缘法向分别摆放在头向、尾向及侧向.

计算状态：俯仰角和滚转角均为0°，S（3GHz）、C（6GHz）、X（10GHz）、Ku（15GHz）4个波段，HH和VV极化.其中0°为机尾方向，180°为机头方向.由表2和图5可得：

1）雷达散射水平.在4个波段，头向、尾向、侧向±30°的RCS算术平均值分别为9.8～14.5dBm2，11.2～14.4dBm2，23.1～27.9dBm2.

2）方位特性.在头向、尾向及侧向附近存在峰值；在C波段，头向RCS峰值达到21.1dBm2，尾向为22.9dBm2，右侧向为41.1dBm2，左侧向为39.5dBm2；侧向RCS峰值范围比头、尾向峰值窄.从图1的几何外形可看出，机身侧向具有曲率半径较大的曲面，产生很强的镜面回波；垂直尾翼在侧向有较强的镜面散射，同时与平尾构成二面角，散射极强；外置起落架也是较强的散射源.在机头方向，复杂桨毂、旋翼操纵系统及起落架系统会有较强的散射；尾桨位于直升机右侧，导致左右两侧RCS不完全对称.

3）极化特性.RCS在HH和VV极化两种情况下变化不大，表明镜面反射占RCS总体水平的主要部分.

4）频率特性.总体上，RCS随入射波频率的增加而增大，主要由镜面散射的高频效应（即镜面散射强度随频率增加而增强）引起.

表2 常规通用直升机RCS算术平均值 dBm2

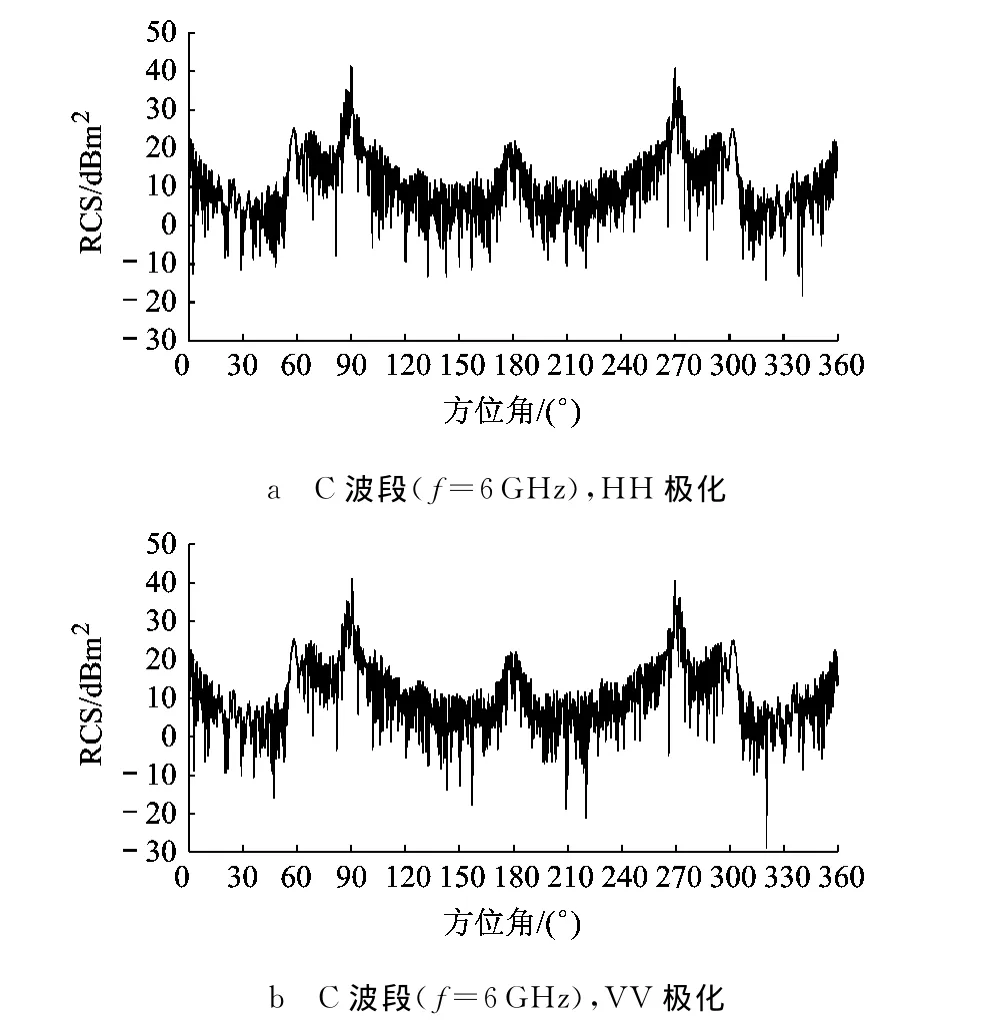
图5 常规通用直升机C波段RCS方位特性

3 通用直升机RCS减缩研究

3.1 RCS减缩外形设计

根据固定翼飞机的低RCS外形设计准则并结合通用直升机几何外形特点，提出通用直升机的隐身设计方法（见图6）：

①将机身及发动机舱横截面设计为近似六边形形状，在机身侧面形成倾斜平面和中间棱边，以取代原型机曲率半径较大的机身侧面；②机头外形分为上下两个曲面，在交界处形成棱边，假设座舱玻璃采用具有全反射的导电镀膜，消除腔体散射；③用桨毂整流罩［14］对复杂的桨毂和旋翼操纵机构进行遮挡；④为消除垂尾后向散射以及与平尾构成的角反射器，采用折线式垂尾；⑤将主起落架收放到进行了外形隐身设计的起落架整流罩中，可避免其占用有效任务容积，后起落架收到尾梁内；⑥旋翼是直升机最主要气动部件，提供了几乎全部升力，还涉及噪声振动［15－17］等学科，难以采取外形隐身措施，在此不做改形研究，保持旋翼桨叶几何尺寸不变，通过改变桨叶数量来进行旋翼RCS减缩研究.

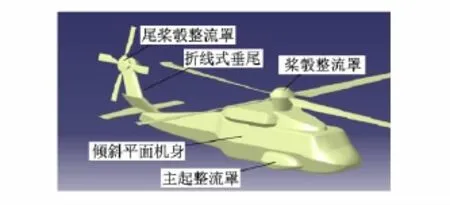
图6 低RCS通用直升机造型

3.2 改形直升机RCS计算

对几何外形改进后的通用直升机进行RCS计算，计算的状态同前.

1）改形直升机机身雷达散射特性.

如表3所示，改形后直升机（不含旋翼尾桨）头向、尾向及侧向±30°RCS均值分别在－9.3～－3.5dBm2，－16.6～ －8.5dBm2，1.5～5.0 dBm2之间.

表3 改形直升机（不含旋翼尾桨）RCS算术平均值 dBm2

2）单独旋翼雷达散射特性.

如表4所示，旋翼在重点方位±30°RCS均值为－7.7～4.5dBm2.结合表3可得，此时在头向及尾向，旋翼的RCS比机身大得多，同时也构成直升机侧向重要散射源.

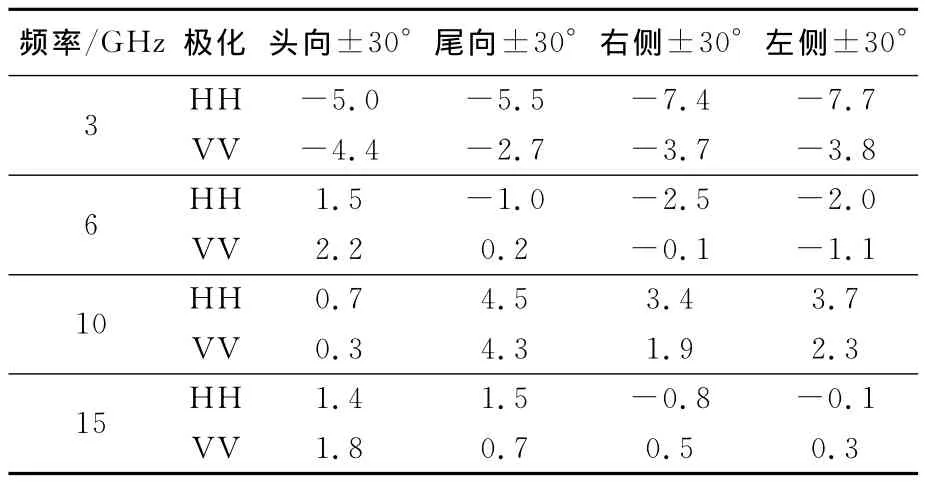
表4 旋翼重点方位RCS算术平均值 dBm2

3）全机雷达散射特性.

由图7和表5可知，在C波段（f＝6GHz）改形后的通用直升机的头向、尾向、左右两侧向RCS峰值分别为20.1，14.6，15.1，17.0dBm2；峰值宽度很窄，不易被雷达跟踪；大部分方位角（50°～360°）的RCS绕－5dBm2上下波动；缩减后的雷达散射水平大为减小，头向、尾向、侧向±30°RCS均值分别为0.3～4.0dBm2，－0.8～5.7 dBm2，－0.2～6.7dBm2；RCS对极化方式的改变较为敏感.

图7 改形直升机C波段RCS方位特性

表5 改形直升机重点方位RCS算术平均值 dBm2

3.3 旋翼RCS减缩研究

旋翼直径很大，桨叶钝头前缘有较强的镜面反射；由式（2）可知，边缘绕射强度与边缘长度平方成正比，所以旋翼后缘的RCS也不容忽视.

许多现役通用直升机的旋翼设计成4片桨叶［11］（如 UH-60“黑鹰”，NH-90等）.此时，总存在一片桨叶前缘法向与另外某片桨叶后缘法向相同，当此法向旋转到重点方位角时，会同时产生较强的镜面反射和边缘绕射.若旋翼选用5片桨叶，桨叶间夹角变为72°，可避免上述强散射源叠加现象.分别将旋翼的前缘法向对着直升机头向，尾向及左右两侧向进行RCS计算（见表6）.

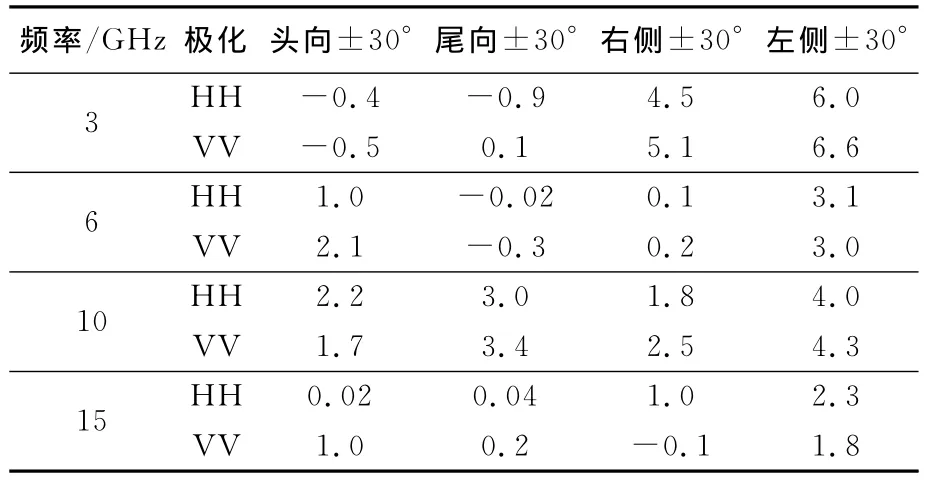
表6 改形直升机（5桨叶旋翼）重点方位RCS算术平均值 dBm2

如表5和表6所示，旋翼桨叶数由4变成5后，头向及尾向±30°RCS算术平均值分别减小了－0.7～3.2dB，0～3.3dB，使雷达散射水平分别在2.2，3.4dBm2以下，减缩效果显著；侧向±30°RCS均值最多减小3dB，极个别频段稍有增加，有一定的减缩效果.

虽然采用5桨叶旋翼，通用直升机在重点方位雷达散射水平有明显改善，但是由图8看来，在机身侧向，旋翼的散射水平与隐身改形后的机身相当；而在头向和尾向，旋翼RCS远比机身大.因此，需要通过使用其他方法（如使用吸波材料等）对旋翼桨叶进行RCS减缩研究，来进一步减缩通用直升机的RCS.

图8 改形机身与单独5桨叶旋翼RCS算术平均值对比

4 气动、静稳定性、重量及有效容积影响

由于直升机旋翼剖面产生的升力大小与剖面所在位置的半径平方成正比［18］，桨毂整流罩（及尾桨毂罩）对其遮挡的旋翼剖面的半径很小，因此对升力影响很小.

采用可收放式起落架不仅能降低雷达散射水平，而且利于改善机身气动阻力；缺点是收放机构会使直升机重量增加.

旋翼桨叶数量增加有利于减小机体振动和桨尖损失，对提高飞行性能有利；缺点是桨毂结构变复杂、重量增加，但现在桨毂技术的发展使其结构简化，重量特性有很大改善［1］.

为了保证直升机的航向静稳定性不变，使倾斜后的垂尾在机身对称面上的投影面积与原垂尾面积相等；保持尾桨位置及倾斜角度不变以避免对直升机飞行操纵造成影响.

RCS减缩后的直升机机身高度不变，最大宽度增加了8%，其机头（设备舱和驾驶舱）及机舱容积为6.2m3，14.8m3，较常规通用直升机的5.9m3，13.9m3，满足容积要求；但机身最大横截面增大了6%，会使机身阻力略有增大.

5 结 论

1）常规通用直升机雷达散射水平较高，头（尾）向及侧向±30°RCS均值分别达到数十平方米和数百平方米；极化效应对RCS影响不大.

2）提出了通用直升机隐身外形设计方法，包括低RCS机身外形和采用5桨叶旋翼方案替代4桨叶旋翼.计算结果表明，隐身改形的通用直升机头（尾）向和侧向的RCS均值分别降低了10～15dBm2和16～28dBm2，相当于常规通用直升机的10%和1%；且改形后直升机静稳定性、飞行操纵及有效容积等基本不受影响.

3）通用直升机RCS减缩后，旋翼相对于机身成为重要散射源，特别是在头（尾）向旋翼RCS远比机身大.因此，若要进一步提高通用直升机的雷达隐身性能，须结合外形及其他方法（如使用吸波材料等）对旋翼桨叶进行RCS减缩研究.

（References）

［1］张呈林，郭才根.直升机总体设计［M］.北京：国防工业出版社，2006：56，151－154

Zhang Chenglin，Guo Caigen.Helicopter preliminary design［M］.Beijing：National Defense Industry Press，2006，56：151－154（in Chinese）

［2］苏东林，宗国民，吕善伟.武装直升飞机雷达散射截面的估算方法［J］.北京航空航天大学学报，1994，20（3）：248－252

Su Donglin，Zong Guomin，LüShanwei.The method of calculation radar cross section of fighting helicopters［J］.Journal of Beijing University of Aeronautics and Astronautics，1994，20（3）：248－252（in Chinese）

［3］叶少波.武装直升机隐身外形优化的计算机辅助设计系统［D］.北京：北京航空航天大学航空科学与工程学院，2004

Ye Shaobo.Computer aided design system to optimize stealthy geometry of armed helicopter［D］.Beijing：School of Aeronautic Science and Engineering，Beijing University of Aeronautics and Astronautics，2004（in Chinese）

［4］蒋相闻，招启军，徐国华.基于面元边缘法的直升机RCS计算与分析［J］.南京航空航天大学学报，2011，43（3）：429－434

Jiang Xiangwen，Zhao Qijun，Xu Guohua.Calculation and analysis of RCS of helicopter based on panel edge method［J］.Journal of Nanjing University of Aeronautics and Astronautics，2011，43（3）：429－434（in Chinese）

［5］Niziolek M.Review of methods used for computational electromagnetics［C］∥Electrodynamic and Mechatronics 2nd International Students Conference Proceeding of the IEEE.［S.l.］：IEEE，2009：15－16

［6］刘战合，武哲，周钧，等.多层快速多级子算法的改进措施［J］.航空学报，2008，29（5）：1180－1185

Liu Zhanhe，Wu Zhe，Zhou Jun，et al.Improving multilevel fast multipole algorithm ［J］.Acta Aeronautica et Astronautica Sinica，2008，29（5）：1180－1185（in Chinese）

［7］Youssef N N.Radar cross section of complex targets［J］.Proceedings of the IEEE，1989，77（5）：722－734

［8］Cui S M，Sakina K，Ando M.A mathematical proof of physical optics equivalent edge currents based upon the path of most rapid phase variation［J］.IEICE Transactions on Electronics，2000，E83-C（4）：659－663

［9］Serim H A，Ergin A A.Computation of the physical optics integral on NURBS surfaces using a radon transform interpretation［J］.IEEE Antennas Wireless Propagation Letters，2008（7）：70－73

［10］白振东，刘虎，武哲.低可探测机身参数化造型与优化［J］.北京航空航天大学学报，2007，33（12）：1391－1394

Bai Zhendong，Liu Hu，Wu Zhe.Parametric modeling and optimization of low observability fuselage in aircraft conceptual design［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33（12）：1391－1394（in Chinese）

［11］倪先平.直升机手册［M］.北京：航空工业出版社，2003 Ni Xianping.Helicopter manual［M］.Beijing：Aviation Industry Press，2003（in Chinese）

［12］韩东，郭荣伟，谭慧俊，等.一种直升机进气道方案的电磁散射特性［J］.南京航空航天大学学报，2002，17（5）：528－532

Han Dong，Guo Rongwei，Tan Huijun，et al.Experimental study of RCS for a helicopter inlet［J］.Journal of Nanjing University of Aeronautics and Astronautics，2002，17（5）：528－532（in Chinese）

［13］阮颖铮.雷达截面与隐身技术［M］.北京：国防工业出版社，1998：99－120.

Ruan Yingzheng.Radar cross section and stealth technology［M］.Beijing：National Defense Industry Press，1998：99－120（in Chinese）

［14］刘军辉.直升机旋翼与桨毂RCS计算和减缩研究［D］.北京：北京航空航天大学航空科学与工程学院，2010

Liu Junhui.Research on RCS calculation and reduction of helicopter rotating blades and hub［D］.Beijing：School of Aeronautic Science and Engineering，Beijing University of Aeronautics and Astronautics，2010（in Chinese）

［15］Ariyur K B，Krstic M.Feedback attenuation and adaptive cancellation of blade vortex interaction on a helicopter blade element［J］.IEEE Transactions on Control Systems Technology，1999，7（5）：596－605

［16］Pearson J T，Goodall R M.Active control of helicopter vibration ［J］.Computing ＆Control Engineering Journal，1994，5（6）：277－284

［17］Shin S，Cesnik C E S，Hall S R.Design and simulation of integral twist control for helicopter vibration reduction ［J］.International Journal of Control，Automation and Systems，2007，5（1）：24－34

［18］约翰逊W.直升机理论［M］.孙如林，译.北京：航空工业出版社，1991：322－326

Johnson Wayne.Helicopter theory［M］.Translated by Sun Rulin.Beijing：Aviation Industry Press，1991：322－326（in Chinese）