基于灰色理论的失效机理一致性检验方法
姚 军 王 欢 苏 泉
(北京航空航天大学 可靠性与系统工程学院,北京 100191)
为尽快预测高可靠、长寿命产品的寿命,通常采用加速试验.它通过提高应力的方式加速产品的失效,从而根据高应力下产品的寿命来外推正常应力下产品的寿命.为了保证这种统计推断的准确性,产品在正常应力和加速应力下必须具有相同的失效机理,这是进行加速寿命试验设计的重要前提[1].
目前,关于加速试验失效机理一致性检验方法的研究,主要分为三类[2].第一类是基于加速模型参数不变的一致性检验方法.其原理是在激活能不变的前提下,可利用产品寿命与温度应力之间的对数线性关系来检验阿伦尼斯、Coffin-Man-son、逆幂率、艾林模型的失效机理一致性.郭春生等人对二极管3DG130进行150~310℃的序进应力加速试验时发现在失效机理不发生改变时,电子器件失效敏感参数的退化速率与施加应力的负倒数遵从指数关系,从而确定了失效机理一致的应力范围[3].该方法缺点在于:第一,失效机理不变的情况下,激活能是否随温度变化,学术界尚未有一个统一的认识;第二,该方法只适用于某几类包含激活能的加速模型,适用范围较局限.
第二类是基于试验观察的失效机理一致性检验方法,主要包括直接观察法、化学分析法、显微镜观察法3种.例如,包亦望等人在研究钛化物陶瓷的高温蠕变行为与失效机理时,对钛化物样品的常温和高温800,1 000,1 100,1 200℃断口进行了扫描电镜微观分析比较,来判别钛化物陶瓷的失效机理一致性[4].与加速试验失效机理一致性检验方法相比,试验观察的方法适用范围更广泛,对失效机理变化的判别更为直接,这种基于试验观察判别方法也有缺点,主要体现在以下几个方面.①有些产品的失效机理变化不容易被观察到,化学分析和显微观察的方法有可能由于技术水平不足或放大倍数不够等原因而没有发现失效机理发生变化的真正应力水平.②该方法在使用上有一定的局限性,化学分析的方法只适用于加速腐蚀试验;显微观察的方法不适用于复杂产品,因为复杂产品失效机理的变化也很复杂,如果将产品每个部分都进行显微分析,工作量会非常大,成本也会非常高,甚至是不可行的,且难以找出由产品各部分的联系引起的失效机理变化;直接观察的方法虽然可以用于复杂产品,但某些产品的失效模式和失效机理不一定一一对应,直接观察法观察到的失效模式变化并不一定代表失效机理发生了变化,没有观察到失效模式的变化也不能说明失效机理就没有变化,这使得直接观察法缺乏说服力.
第三类是基于统计方法的一致性检验方法,如针对威布尔分布的产品形状参数一致性检验等.这种方法的原理是若产品的失效机理不变,则加速系数是与可靠度值无关的常数,由加速系数与可靠度值无关可以推出产品寿命分布的变异系数不变.这样,只要对变异系数进行假设检验,若变异系数发生变化,则可推出失效机理发生了变化.文献[5]给出了常见19种寿命分布的失效机理不变条件,其中关于Weibull分布、对数正态分布、Gamma分布的失效机理不变条件与文献[6]根据试验结果与工程经验得出的结果一致.与前两种方法相比,该方法适用范围更广泛.这种方法也有缺点,主要表现为:①统计方法的假设物理意义不明确,没有从物理的角度给出变异系数与机理的关系;②目前统计方法只能用于加速试验数据,只能用于事后检验,不能在加速试验之前对其进行理论指导.
材料是任何产品的物质基础,产品的失效在广义上一般都可归结为材料失效.失效机理的变化是材料本身属性的变化,在某种确定的外因(应力、温度、介质等)条件下,只呈现出某种确定的材料属性.因此,若外因到达失效机理变化点,材料内部会发生某种物理化学或结构上的变化(如合金的同素异构过程、树脂的玻璃化过程等),致使材料属性发生变化,引起产品的失效机理变化,表征到宏观结构就是产品被测性能参数的突变[7-8].灰色理论是一种处理少数据不确定性问题的理论,GM(1,1)建模方法是灰色理论的一个重要分支,可解决少数据寿命预测问题[9-10].等维新息模型是一种在选择建模数据时以最新的实际数据作为参考点,去掉老数据,保存数列等维,依次建模的一种模型.本文采用GM(1,1)建模方法与等维新息模型结合的一种预测方法,对预试验数据进行建模,得出各应力点性能预测值后与实际值进行残差计算,观察残差点的突变情况,以此来找寻失效机理的变化点.
1 理论分析
1.1 基于GM(1,1)方法的灰色预测模型
设预试验中得到的性能退化序列为

其中,ξ(0)(1)为最小应力对应的性能数据;ξ(0)(n)为最大应力对应的性能数据.
为将不同极性的性能退化序列转化为同极性(最大值极性)的序列,将ξ(0)按式(1)进行一阶累加,灰生成新序列[10]
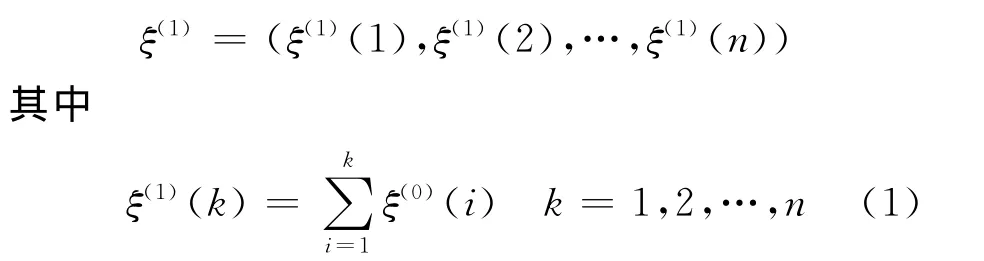
将性能退化序列累加后,弱化了其随机性,由于建立的模型是1阶1变量序列,可采用GM(1,1)模型建模方法,则可认为ξ(1)满足一阶线性微分方程[4].

式中,a为发展灰数,反映了性能退化序列ξ(0)和累加性能退化序列ξ(1)的发展趋势;u称为内生控制灰数,反映了数据间的变化关系.
为求解a与u,令=[a,u]T为待估向量,由于性能退化序列是离散的,将式(2)中离散化,则有

其中,Z(1)(k)为式(2)的背景值;μ为权重系数,μ∈[0,1].
根据灰色预测方法,一般μ取值为0.5,则

将式(2)离散化后,可得到累加生成性能退化序列的离散化公式

利用最小二乘法对式(6)进行求解,可得出待估参数为

根据得出的待估参数,代入式(2),可求解出累加生成性能退化序列ξ(1)的预测值为

对式(8)累减还原可得性能退化序列的预测模型为
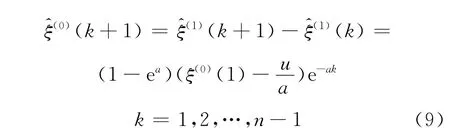
1.2 基于等维新息模型的预测方法
虽然,式(9)可以作为长期预测模型,但真正具有实际意义、精度较高的仅仅是ξ(0)(n)以后的一两个数据,其他更远的数据不是预测数据而是规划性的数据.可以认为越往未来发展,模型计算的预测数据,其预测意义就越小.随着系统的发展,老数据的信息意义将逐步降低,在不断补充新信息的同时,及时地去掉老信息,建模序列更能反映系统在目前的特征.
基于GM(1,1)方法的建模数据允许做不同的取舍,但必须等距、相邻、不得有跳跃.在选择建模数据时以最新的实际数据作为参考点,去掉最老的数据,保持数列等维,依次建模,这样建立的模型就是等维新息模型.
在预测前,必须确定模型的维度,为使模型达到最高的精度,可选择维度分别为4~11维(至少为4).
1.3 基于灰色理论的失效机理一致性检验方法
1)选择适当的维度,对强化试验数据建立等维新息模型;
2)根据数据的特点选择适当的灰色模型对等维新息模型中的每一段数据进行预测,得到一个预测值;
3)将预测值与对应的真实值进行比较,计算残差;
4)观察残差是否发生显著的变化,若有,找出第一个显著变化点,则认为该点对应的地方机理发生了变化,若没有显著变化,则认为产品的机理在强化试验中没有发生变化.
2 分析实例
2.1 试验样品
本次预试验围绕某型号卫星雷达天线驱动机构上用光电编码器展开,影响编码器可靠性的环节主要是发光二极管、光敏三极管在空间热环境及辐射环境下性能漂移.本次试验样品为配对使用的红外固体发光二极管(型号:OP224TXV)及光敏三极管 (型号:OP604TXV),图 1 为OP224TXV及OP604TXV的外观图,图2为两器件配对使用连接示意图.考察的性能参数为接收元件光敏三极管信号幅值.

图1 OP224TXV(左)及OP604TXV(右)外观图

2 OP224TXV(左)及OP604TXV(右)配对使用连接图
2.2 试验步骤
试验开始前,常温下测量样品的性能参数,作为试验中比较的基准.试验中每个温度台阶驻留时间为1h,前10min(t1)为保温阶段,后50min(t2)初始和末端各测量一次性能参数.初始环境温度为95℃,初始步进量级为10℃,每次试验将试验中测试数据与初始测试数据进行比较,观察其性能退化趋势,试验剖面如图3所示.试验设备如图4所示,测试设备如图5所示.

图3 工作电应力下温度极限试验剖面

图4 试验设备

图5 测试设备
2.3 试验数据分析及处理
预试验数据如表1所示.

表1 光电编码器强化试验数据
试验数据共10个,选择等维新息模型的维度为4,对各数据段进行建模,计算出发展系数a,见表2.

表2 各数据段灰色预测的发展系数
用各数据段建立的预测模型推测后一个性能参数值,例如,用1~4数据建立的预测模型来推测第5个性能参数值,并与实际观测值进行对比,计算残差,如表3.用表3数据,作预测值及观测值走势图,如图6,为检验残差突变点,作残差图,见图7.从图6可以看出,预测值及观测值的整体趋势呈下降趋势,在165℃之前,预测值及观测值下降幅度很小,在各应力观测点的预测值及观测值大小交替;从图7可以看出,135,145,155和165℃的残差值在0的上下浮动,在175℃附近,残差出现突变点,可以判定此处性能参数发生了突变,失效机理发生了改变.

表3 信号幅值的预测值、真实值及残差

图6 各温度应力下观测值及预测值走势

图7 各温度应力下残差
2.4 基于统计方法的失效机理一致性检验
为验证试验件在175℃附近发生失效机理变化,采用加速寿命试验数据进行基于统计方法的失效机理一致性检验分析,加速寿命试验数据如表4,产品失效判据为光敏三极管的信号幅值降至初值的60%以下.

表4 光电编码器加速寿命试验数据
假定光电编码器在各温度应力台阶下其失效时间服从威布尔分布,威布尔的变异系数为形状参数m,即从形状参数的变化可以表征失效机理的变化.计算各温度应力下的威布尔形状参数m,可以得出:160℃时,m=29.3;175℃ 时,m=16.017 2;190℃时,m=13.719 2;220℃时,m=13.16.很明显,在175,190及220℃时,m值基本一致,其失效机理一致,而160℃时,m值明显大于其他应力水平,其失效机理与其他应力情况下的不一致,也就是说,在175℃附近,失效机理发生了改变.与基于灰色理论失效机理一致性检验方法做出的判断一致.
2.5 失效机理分析
影响信号幅值变化最根本的原因在于发光二极管的光功率的衰退.对于发光二极管来说,造成光功率的衰退可能有两方面的原因:LED结温的产生和LED热阻的生成.
LED结温是指P-N结区的温度,其形成是由于LED空穴、电子运动,一部分能量产生有效的光电效应,发出光子;另一部分是以发热的形式消耗掉了,从而导致P-N结区芯片发热.对于一个封装好的LED发光管来说,产生结温最重要的因素在于LED封装的散热能力.LED热阻是LED散热通道上的两个节点之间热功率流的阻值,其封装的材质及形式对LED热阻的产生有很大的影响.
试验用LED发光管其封装环氧胶在高温下会发生变性、发黄,出光效率下降衰减.且LED用的封装环氧胶存在着一个重要特性,即当环氧胶温度超过一个特定温度时,封装环氧的特性将从一种刚性的类玻璃状态转变成一种柔软的似橡胶态状的物质.此时材料的膨胀系数急剧增加,形成一个明显的拐点,这个拐点所对应的温变即为环氧树脂的玻璃状转化温度,当器件在此温度附近或高于此温度变化时,将发生明显的膨胀或收缩,致使二极管发光功率出现明显衰退.
对试验用二极管环氧胶为双酚A型环氧树脂胶,图8为双酚A型环氧树脂胶在140℃(左上)、160℃(右上)、170℃(左下)、180℃(右下)温度下 断 裂 面 (SEM,Scanning Electron Microscope)照片.从图8可以看出,在140℃及160℃,胶粘剂成刚性状态,而170℃时,胶粘剂成絮状物的橡胶形态,180℃则更加明显.由此可知,170℃左右为封装用环氧胶材料属性变化温度点,该材料属性的变化致使产品失效机理发生改变,所以从宏观上能观察到在175℃处,接受元件光敏三极管信号幅值残差出现突变点.

图8 胶粘剂断裂面SEM图
3 结束语
本文提出了一种基于灰色理论的失效机理一致性判别方法,它克服了传统方法的缺陷,与基于统计的方法相比,此方法仅需要预试验数据就可对失效机理一致性进行检验,可指导加速寿命试验.与基于试验观察的方法对比,此方法仅需要少量数据就可做出准确的检验,简单明了.与基于加速模型参数不变的方法相比,本方法从本质上来说是一种统计方法,与失效机理、激活能等物理化学理论无关,应用范围更为广泛.
(References)
[1]茆诗松,王玲玲.可靠性统计[M].上海:华东师范大学出版社,1984
Mao Shisong,Wang Lingling.Reliability statistics[M].Shang hai:East China Normal University Press,1984(in Chinese)
[2]Pan Xiaoxi,Huang Xiaokai,Chen Yunxia,et al.Connotation of failure mechanism consistency and identification method for accelerated testing[C]//Prognostics and System Health Management Conference.[S.l.]:IEEE,2011:1-7
[3]郭春生,谢雪松,马卫东,等.加速试验中失效机理一致性的判别方法[J].半导体学报,2006,27(3):560-563
Guo Chunsheng,Xie Xuesong,Ma Weidong,et al.Failuremechanism identification method in accelerated testing[J].Journal of Semiconductors,2006,27(3):560-563(in Chinese)
[4]包亦望,苏盛彪,王毅敏,等.钛化物陶瓷的高温蠕变行为与失效机理[J].硅酸盐学报,2002,30(3):300-304
Bao Yiwang,Su Shengbiao,Wang Yimin,et al.High-temperature creep and failure mechanism of ceramics containing titaniferous compound[J].Journal of the Chinese Ceramic Society,2002,30(3):300-304(in Chinese)
[5]周源泉,翁朝曦,叶喜涛.论加速系数与失效机理的不变的条件(I)-寿命型随机变的情况[J].系统工程与电子技术,1996(1):55-67
Zhou Yuanquan,Weng Chaoxi,Ye Xitao.Study on accelerated factor and conditionfor constant failure mechanism(Ⅰ)—the case for lifetime is a random variable[J].Journal of Systems Engineering and Electronics,1996(1):55-67(in Chinese)
[6]Nelson W.Analysis of accelerated life test data-part I:the arrhenius model and graphical methods[J].Transactions on E-lectrical Insulation,1971,6(4):165-181
[7]盐见弘.失效物理基础[M].杨家铿译.北京:科学出版社,1982
Shiomi Hiroshi.Basis of failure physics[M].Translated by Yang Jiakeng.Beijing:Science Press,1982(in Chinese)
[8]Hu J M,Barker D,Dasgupta A,et al.Role of failure-mechanism identification in accelerated testing[C]//Proceedings Annual Reliability and Maintainability Symposium.Las Vegas.NV:IEEE,1992:181-188[9]Atwa Y M,El-Saadany E F.Annual wind speed estimation utilizing constrained grey predictor[J].Transaction on Energy Conversion IEEE,2009,24(2):548-550
[10]邓聚龙.灰色系统基本方法[M].武汉:华中科技大学出版社,2005
Deng Julong.Basic methods of gray system[M].Wuhan:Huazhong University of Science and Technology Press,2005(in Chinese)
[11]Chang B R,Tsai H F.Forecast approach using neural network adaptation to support vector regression grey model and generalized auto-regressive conditional heteroscedasticity[J].Expert Systems with Applications,2008,34(2):925-934
[12]Huang K Y,Jane C J.A hybrid model for stock market forecasting and portfolio selection based on ARX grey system and RS theories[J].Expert Systems with Applications,2009,36(3):5387-5392
[13]Truong D Q,Ahn K K.Force control for hydraulic load simulator using self-tuning grey predictor-fuzzy PID [J].Mechatronics,2009,19(2):233-246
[14]Kayacan E,Ulutas B,Kaynak O.Grey system theory-based models in time series prediction[J].Expert Systems with Applications,2010,37(2):1784-1789

