切削参数对汽轮机叶片精加工变形影响

董久虎 谌永祥 蒋 波 李双跃

(西南科技大学制造科学与工程学院，四川绵阳 621010)

汽轮机叶片的加工质量是影响其工作效率的主要因素之一。叶片的进、出汽边的厚度较薄，在加工过程中，由于切削力作用，汽轮机叶片会发生变形，产生加工误差。为保证叶片的加工精度，在实际加工过程中往往采用比较保守的加工方法，采用很小的主轴转速和切削深度，以降低叶片加工效率为代价。另外，采用填充的方法可以增加叶片的刚度，但是操作复杂，降低了加工效率;而且由于蜡、石膏、松香等填充材料的收缩和膨胀效率难以控制，很难满足高精度要求［1］。

为了研究切削参数对叶片受力变形的影响，文献［2－5］对切削加工力学模型做了大量研究。以切削力的数学模型为基础，文献［6－8］对在不同的切削条件下对薄壁零件的加工变形进行了有限元数值模拟分析;Budak E等［9］通过减小进给量来控制薄壁零件的变形;Zbignizew Lechnink等［10］通过优化刀具轨迹，实现对叶片的误差补偿;岩部洋育［11］通过使用双主轴同时加工，减小了薄壁零件的加工变形。本文在三轴数控机床的球头铣刀模型基础上，建立了应用于五轴数控机床的球头铣刀加工汽轮机叶片的数学模型，从而可以计算出叶片在加工过程中受到的切削力大小。分别在不同切削速度、切削深度、进给速度条件下，应用有限元ABAQUS软件对叶片变形进行数值模拟分析，得到叶片变形量的大小。通过正交实验分析切削参数，进给速度和主轴转速的交互作用对叶片变形的影响。正交实验表明:主轴转速、进给速度、主轴转速和进给速度的交互作用对叶片变形的影响显著，切削深度对叶片变形量的影响不显著。

1 切削力数学模型建立及叶片变形模拟

1.1 球头铣刀数学模型的建立

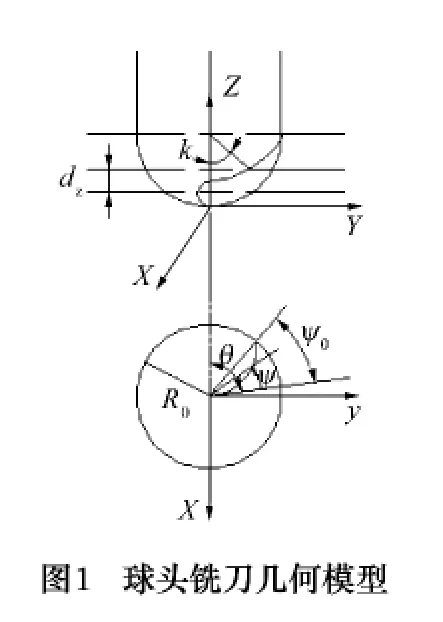
在计算球头铣刀加工叶片时的切削力大小时，可以将切削刃离散成很多微元切削刃。通过计算每个切削刃作用在叶片上的力，将其求和，便可求得球头铣刀在加工叶片时，作用在叶片上的沿3个坐标方向的力。任意一个微元切削刃的空间位置可以通过以下3个参数确定:轴向高度z(j)，有效切削半径r(z)和螺旋滞后角ψ(z)，其中j为微元切削刃的编号，最靠近铣刀刀尖处的微元切削刃编号为1，沿轴向依次增加至Nz，令i为铣刀刀刃编号，刀尖位于y轴上的刀刃为1号，最大编号为Nf，则第i个切削刃上，轴向高度为z(j)处的微元切削刃的空间位置角φ(i，z)及ψ(z)、r(z)可分别表示为［12］:

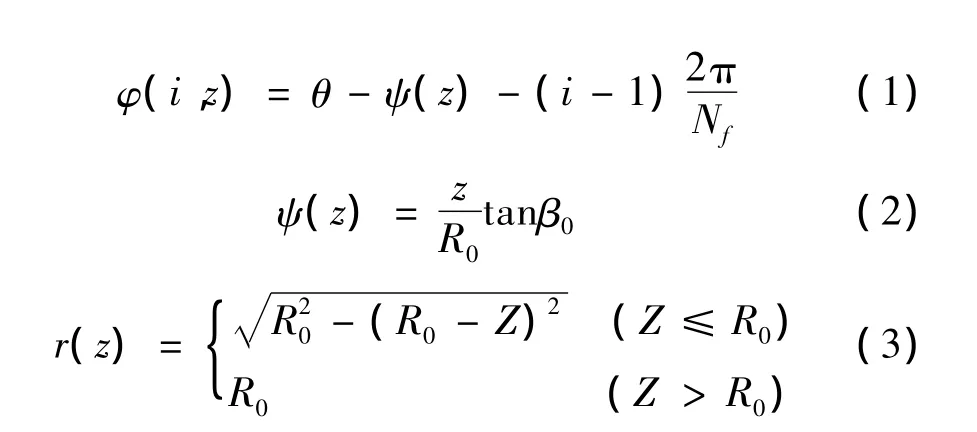
式中:θ为从铣刀坐标系y轴正向开始的铣刀转动角度。

高度为z的微元切削刃的轴向浸切角k(z)(微元切削刃法线方向和刀具轴线方向夹角)可表示为:

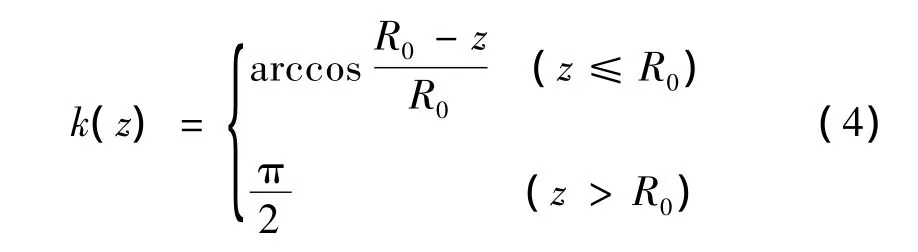
1.2 球头铣刀切削力建模

将球头铣刀切削刃离散为一系列很小的微元切削刃，刀具受到的切削力即为所有参与切削的微元切削刃受力的矢量之和。根据切削力产生机理可以有以下公式［13］:

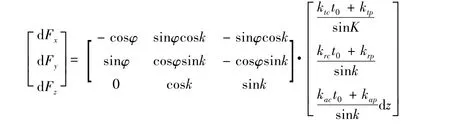
切削力系数见表1，根据公式(5)可以求得3个方向切削力的大小。

1.3 球头铣刀加工叶片简化模型

汽轮机叶片一般采用五轴数控加工，加工过程十分复杂，为便于分析加工过程中叶片的受力变形情况，可将加工过程中瞬时叶片的切削模型简化成如下形式:球头铣刀加工叶片时，切削刃与叶片接触，将接触点看作微小的直线段，将直线段延长，形成一直线。可将刀具对此接触点的加工假设为加工该直线。

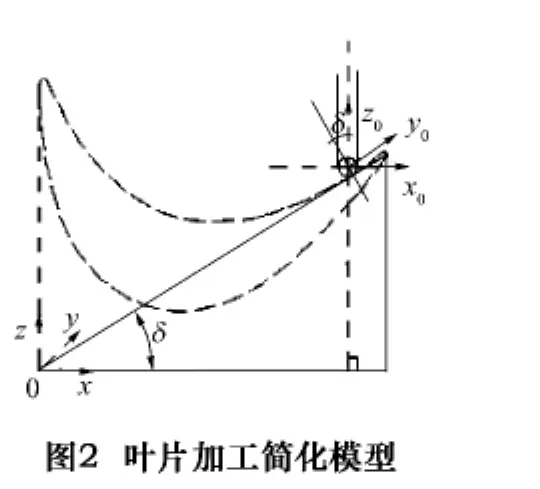
五轴数控加工汽轮机叶片过程中，刀具与工件表面的夹角随着加工过程不断变化，为了分析此加工过程，建立瞬时工件坐标系和刀具柱面坐标系:将刀具所在的直线为Z轴，垂于刀具且通过球头铣刀球心的直线为X轴，球头铣刀的加工倾角为假设的加工斜线的法线方向与刀轴所在的直线间的夹角δ，如图2所示。

由于叶片在精加工过程中，切削力比较小，沿着叶片截面方向的切削分力对叶片变形的影响比较小，忽略其对叶片变形的影响。将其他两个方向的切削分力分解，可以求得垂直于叶片加工表面的切削合力F为

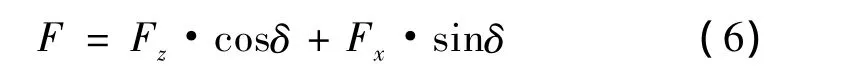
式中:δ为球头铣刀的加工倾角。由式(6)可以看出，垂直于叶片表面的切削合力F的大小只与Fx、Fz和球头铣刀的加工倾角δ有关。

1.4 叶片加工变形量求解

为了求解切削要素对叶片加工变形的影响，以硬度为30HRC的45号钢的材料为例，刀具直径为16 mm，螺旋角为30°，刀具的加工倾角δ为30°。球头铣刀的切削系数［13］如表 1。

根据建立的球头铣刀加工叶片的数学模型，求解沿3个坐标方向的切削力。应用有限元软件ABAQUS对叶片变形进行数值模拟分析，得到叶片的变形量如图3所示，图中将叶片的变形量放大了105倍。

表1 球头铣刀切削力系数

2 正交试验与结果分析

2.1 正交实验设计

为了分析叶片在精加工过程中，切削要素对叶片变形的影响，设计了一级交互作用的正交实验。主要影响因素有主轴转速、进给速度、切削深度、主轴转速和进给速度交互作用，评价指标是叶片变形量。因素水平表见表2，正交实验分析见表3，方差分析见表4。

表2 因素水平表

表3 正交实验分析表

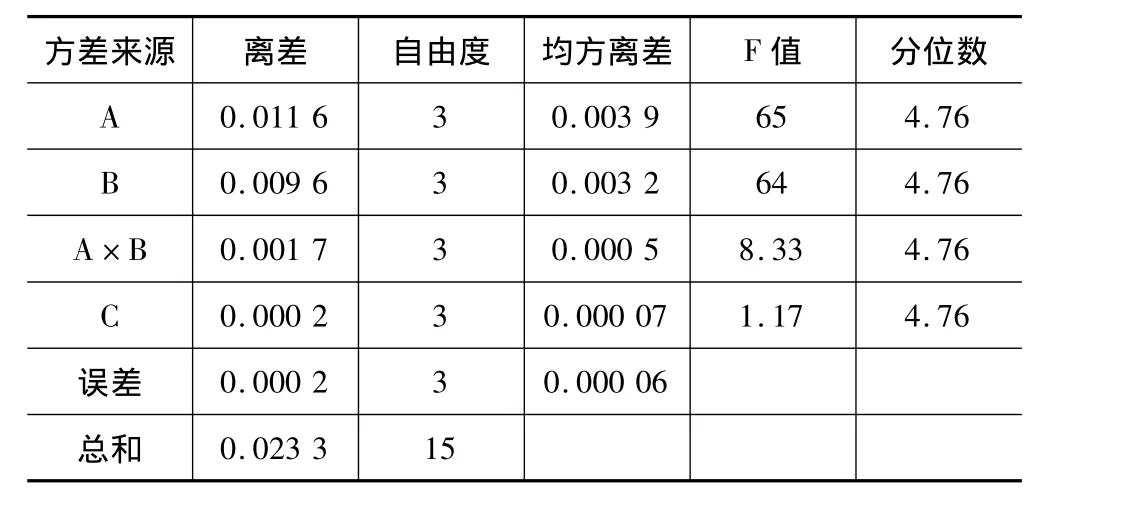
表4 方差分析表

2.2 切削参数对叶片精加工变形的影响

根据表3中的数据，可以得到如图4所示的各个因素对叶片变形的影响趋势图。

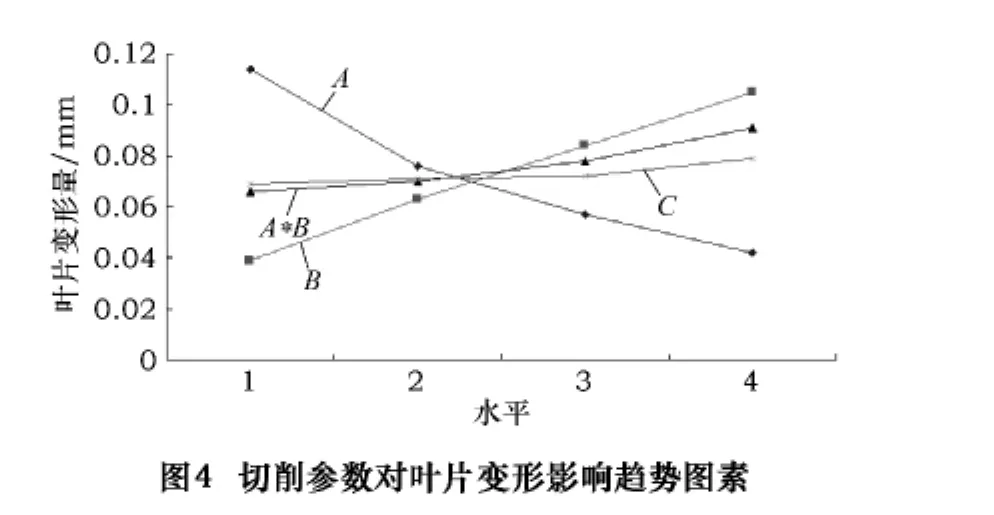
从图4中可以看出:叶片变形量随着主轴转速的增加而减小，主要是因为在一定的切削条件下，增加主轴转速，可以减小球头铣刀的每齿进给量，减小了切削力的大小，从而减小了叶片的变形量;叶片变形量随着进给速度增加而增大，主要是因为在一定的切削条件下，增加进给速度，提高了球头铣刀的每齿进给量，增大了切削力的大小，从而增大了叶片的变形量;叶片变形量随着切削深度的增加而增大，因为切削深度增加，球头铣刀的切削面积增加，增加了切削力的大小，从而增大了叶片的变形量。

2.3 极差与方差分析

由表3中的极差数据可知，RA＞RB＞RA×B＞RC。因此，这四因素对叶片变形影响大小的排列顺序为:主轴转速＞进给速度＞主轴转速和进给速度一级交互作用＞切削深度，最佳的切削参数组合为A4B1C1，较小的进给速度和切削深度固然能够减小叶片的加工变形，提高叶片的加工精度。但是，在实际加工过程中，必须考虑叶片的加工效率。因此，叶片的切削要素应选择较大的主轴转速，在保证加工精度的前提下，适当的提高进给速度和切削深度。

根据表4中的方差表，给定显著性水平α=5%，查表得F0.05(3，3)=4.76。由方差分析表可知，FA、FB、FAB均大于4.76，即主轴转速、进给速度、主轴转速和进给速度一级交互作用对叶片变形的影响显著，因为在叶片精加工过程中，主轴转速和进给速度比较大，主轴转速和进给速度决定了球头铣刀每齿进给量的大小，从而决定了叶片变形的大小;FC的值小于4.76，即切削深度对叶片变形的影响不显著。因为在精加工过程中，切削深度相对比较小，其值基本为0.3 mm左右，切削深度的增加对端铣刀的切削面积的大小影响不大，对切削力的大小影响比较小，从而对叶片变形影响比较小;而在粗加工过程中，切削深度比较大，切削深度的大小对叶片变形影响比较大。

3 结语

(1)在球头铣刀数学模型的基础上，建立了球头铣刀加工汽轮机叶片的切削力数学模型，为研究汽轮机叶片变形提供了方法。

(2)通过正交实验，获取了汽轮机叶片在精加工过程中切削要素对叶片变形的影响。主轴转速和进给速度对叶片变形的影响比较显著;由于在精加工过程中，切削深度相对较小，对叶片变形的影响不是很明显。

(3)在薄壁零件加工过程中，为了提高零件的加工精度，应选择较大的主轴转速、较小的进给速度、较小的切削深度;为了提高叶片的加工效率，应该选择较大的进给速度，适当提高进给速度，较大的切削深度。

［1］胡创国，张定华，任军学，等.切削力建模方法综述［J］.力学进展，2006，36(4):564 －570.

［2］Lee P，Altintas Y.Prediction of ball－end milling forces from orthogonal cutting data［J］.International Journal of Machine Tools and Manufacture，1996，36(9):1059 －1072.

［3］Kim G M，Cho P J，Cutting force prediction of sculptured surface ball end milling using Z －map［J］.International of Machine Tools＆ Manufacture，2000，40(2):277 －291.

［4］Gradisek J，Kalveram M，Weinert K.Mechanistic identification of specific force coefficients for a general end mill［J］.International of Machine Tools＆ Manufacture，2004，44(4):401－414.

［5］Chung－ lang Tsai，Yunn － shiuan Liao.Prediction of cutting force in ball－ end milling by means of geometric analysis［J］.Journal of Materials Processing Technology，2008，205(1 －3):24 －33.

［6］Devor R E.Control of surface error in end milling［A］.Eleventh North American Manufacturing Research Conference Proceedings［C］，1983.

［7］Ee Meng Lim.Error compensation for sculptured surface productions by the application of control surface strategy using predicted machining errors［J］.Journal of Manufacturing Science and Engineering，1997，119(8):402－409.

［8］Jer－Shyong Tsai.Finite－ element modeling of static surface errors in the peripheral milling of thin － walled workpieces［J］.Journal of Materials Processing Technology，1999，94:235 －246.

［9］Budak E，Altintas Y.Modeling and avoidance of static form errors in peripheral milling of plates［J］.Int.J.Mach.Tools Manufact Ind，1995，35(3):459 －476.

［10］Zbigniew Lechniak.Methodology of off－line software compensation for errors in the machining process on the CNC machine tool［J］.Journal of Materials Processing Technology，1998，76:42 －48.

［11］岩部洋育.High accurate machining of thin wall shape workpiece by endmill［C］.日本学会论文集，1999.

［12］孙梦琴，翁泽宇.球头铣刀切削力模型的研究成果［J］.工具技术，2006，40(9):7 －9.

［13］王启东，刘占强，汤爱民，等.球头铣刀瞬态切削力数学模型建立与仿真［J］.农业机械学报，2012，42(8):200 －206.