聚晶金刚石高速研磨温度场的有限元分析*

许立福 刘 涛 黄树涛 周 丽

(沈阳理工大学机械工程学院，辽宁沈阳 110159)

聚晶金刚石(Polycrystalline Diamond，简称PCD)具有接近天然金刚石的硬度、耐磨性以及与硬质合金相当的抗冲击性，化学性能稳定，在精密切削等领域得到广泛应用［1］。PCD的精密加工方法之一就是采用金刚石砂轮进行研磨加工。研磨时高速旋转的砂轮与工件表面接触摩擦，产生摩擦热，大部分热量被传入工件，引起工件表层局部的高温。高温一方面有利于PCD材料的去除及研磨表面粗糙度值的减小;另一方面过高的温度会导致研磨表面的热损伤，出现严重石墨化，降低聚晶金刚石使用寿命和工作可靠性［2］，同时高温也会导致砂轮磨损加快。因此，研究聚晶金刚石高速研磨时表面温度的分布状况，对提高研磨效率和研磨质量，有效控制热损害，深入探讨聚晶金刚石的高速研磨机理等具有重要意义。

本文采用三维热－力耦合有限元法分析了使用金刚石砂轮高速研磨聚晶金刚石圆片时，在不同工艺参数下，摩擦热所形成的温度场分布规律，为聚晶金刚石的高速研磨实验及研磨机理研究提供理论依据。

1 有限元分析

1.1 PCD片与砂轮实体模型的建立

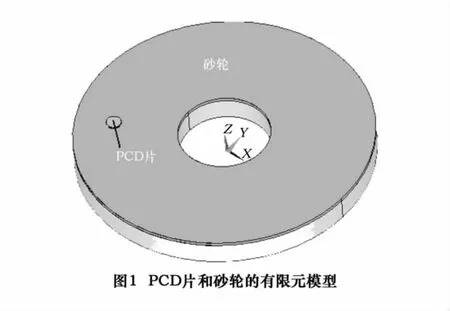
根据聚晶金刚石高速研磨装置，建立图1所示PCD片与金刚石砂轮的温度场分析有限元模型，在保证计算精度的条件下，为了提高计算效率，对模型结构进行了合理简化。其中砂轮的直径为260 mm，基体厚度20 mm，工作层厚度3 mm。PCD片为直径13 mm，厚度2 mm的圆片，PCD层与硬质合金层厚度各为1 mm，PCD圆片中心距砂轮中心110 mm。

1.2 材料特性及单元类型

金刚石砂轮的基体为铝合金，工作层为树脂与金刚石磨粒的混合物，浓度75%的树脂结合剂金刚石砂轮的机械及热特性如表1。

PCD片与砂轮之间的摩擦生热问题属于热结构耦合场分析，其变形和传热发生在同一空间域和时间域，可以采用ANSYS提供的耦合场三维六面体单元SOLID5来进行单元划分。SOLID5单元有8个节点，每个节点最多有6个自由度。

表1 有限元计算中的材料特性［3－4］

1.3 载荷与边界条件

为了分析PCD片与金刚石砂轮相对高速旋转运动时摩擦热的温度分布情况，使砂轮相对于PCD做旋转运动，PCD片固定不动，并在其上方施加一定的压力载荷。施加的砂轮转速分别为1 500、2 000、2 500、3 000、3 500、4 000、4 500、5 000 r/min。压应力载荷分别为 2、4、6、8、10 MPa。对比分析冷却和不冷却两种情况下的温度场分布情况。

传热过程开始时，PCD片、砂轮表面及内部的温度为环境温度，即有限元分析时的初始温度。由于热－力耦合分析过程中的时间较短，为了使温度场分布更明显，适当提高初始温度T0，取T0=50℃，得到温度初始条件:

式中:t为时间，s;T0为初始温度，℃。

考虑到PCD片与砂轮之间的热辐射损失、热传导及热对流较少，计算时忽略了热辐射的影响。边界条件包括已知热流密度的第二类边界条件和已知对流传热系数的第三类边界条件。边界条件可表示为［5］:

式中:q*为热流密度;λnn为热导率;∂T/∂n为沿向的温度梯度;hf为表面传热系数;TS为固体表面的温度;TB为周围环境的温度。

将角速度载荷转化为切向位移载荷施加在砂轮上，PCD片上表面施加压应力载荷和冷却时的温度载荷。

2 计算结果分析

2.1 温度场的分布规律

图2和图3所示分别为无冷却和有冷却两种情况下，砂轮转速3 000 r/min，压应力载荷10 MPa时，聚晶金刚石研磨表面温度场随时间的分布及变化云图。PCD圆片左侧为外边缘(距砂轮中心较远处)，右侧为内边缘，下侧为研磨切入点，上侧为切出点。从图中可以看出，冷却与不冷却两种情况下研磨表面温度场的分布及随时间的变化趋势非常相似，最高温度都分布于外边缘处，最低温度则分布在内边缘处，只是冷却时的表面温度值较低。在研磨开始时，下侧切入点处温度比上侧切出点处温度高，但随着研磨时间的增加，切出点的温度逐渐升高，当研磨一段时间后，切出点处温度超过了切入点处温度，并持续下去直到研磨结束。

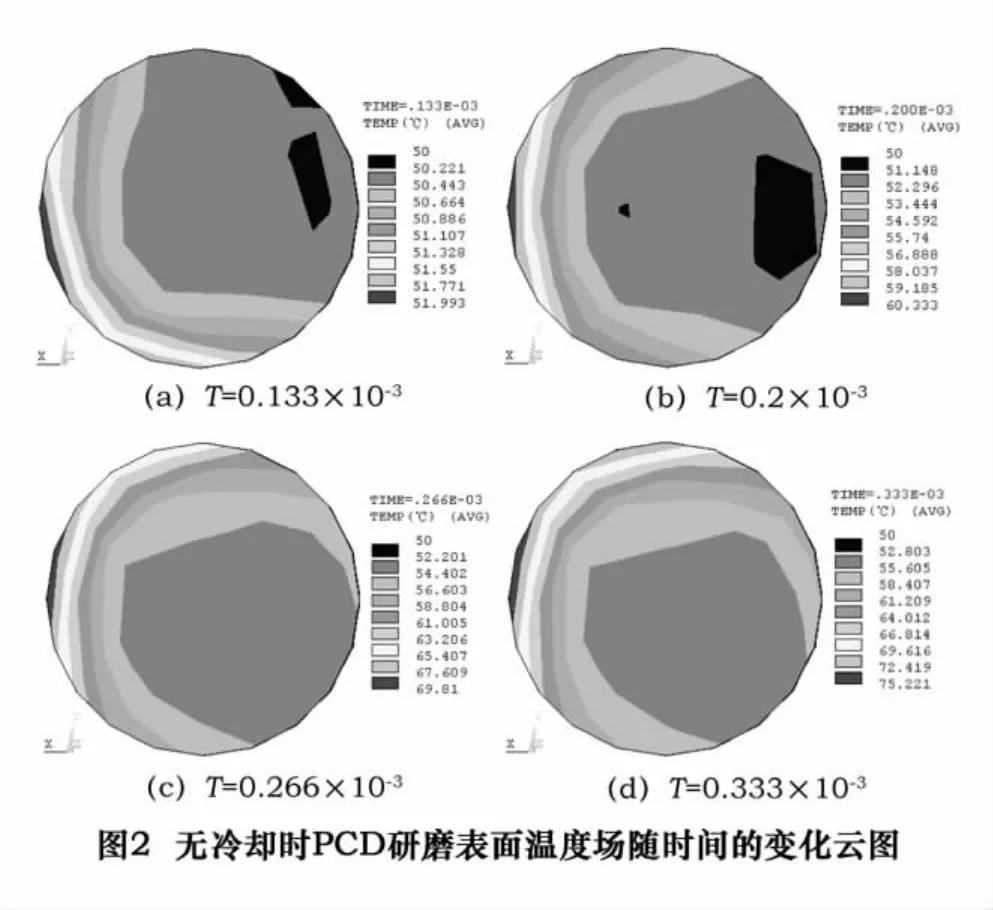
出现上述现象的主要原因是，研磨过程中PCD片外边缘处的研磨线速度大于内边缘处，摩擦产生的热量多，使得外边缘处温度高于内边缘处，内外边缘处温度差值的大小主要取决于研磨线速度差值的大小。研磨切入点处和切出点处线速度相同，随着研磨时间的增加，切入点处的一部分热量经过砂轮传递到切出点处，使得切出点处的温度逐渐高于切入点处。

其他转速和载荷条件下温度场随时间的分布和变化规律与上述情况相似，这里不再一一列出。

2.2 研磨参数对温度场的影响

(1)研磨时间对温度的影响

图4所示为砂轮转速3 000 r/min，压应力载荷10 MPa时，PCD片研磨表面最高温度与研磨时间的关系曲线。可以看出，最高温度随着研磨时间的增加而升高，开始时温度升高速度较慢，随后快速升高，最后升高速度又趋于平缓，类似“S”型曲线。不冷却情况下温度的最高值始终比冷却时大，而且两者之间的差值随时间的增加也逐渐变大。

(2)研磨速度对温度的影响

图5为研磨时间相同，压应力载荷10 MPa时，PCD研磨表面最高温度随砂轮转速的变化情况。可以看出，研磨表面的最高温度随着砂轮转速的增加而增高，基本呈线性关系。不冷却时温度的最高值始终大于冷却时的情况，两条线基本平行。

(3)研磨压力对温度的影响

图6为研磨时间相同，砂轮转速3 000 r/min时，PCD研磨表面的最高温度随研磨压应力的变化情况。可以看出，研磨表面的最高温度随着压应力的增加而增高，在压应力小于6 MPa时，温度的升高幅度较快，随后温度升高趋势变缓。不冷却时的温度最高值始终大于冷却时的情况。

3 结语

采用三维热－力耦合有限元法分析了使用金刚石砂轮高速研磨聚晶金刚石片时，不同工艺参数下温度场的分布和变化规律。

(1)冷却情况下聚晶金刚石研磨表面的温度始终比不冷却时的低。

(2)不同工艺参数条件下，PCD研磨表面温度场的分布情况基本相似，温度的最高值都出现在研磨表面的外边缘处，即研磨线速度最大处。研磨开始时，研磨表面切出点处温度低于切入点处，随着研磨时间的增加，切出点处温度逐渐升高并超出切入点处温度。

(3)PCD研磨表面温度随着研磨时间增加、砂轮转速升高和研磨压力的增大而升高，只是升高的趋势有所不同。

［1］李颖，龙旭辉.金刚石聚晶的性能［J］.郑州工业学校学报，2001(4).

［2］王光祖.聚晶金刚石(PCD)在工业中应用［J］.超硬材料与工程.1996(3):15－20.

［3］机械设计手册编委会.机械设计手册:第一卷［M］.北京:机械工业出版社，2004.

［4］袁哲俊，刘华明.金属切削刀具设计手册［M］.北京:机械工业出版社，2008.

［5］张国智，胡仁喜，陈继刚.ANSYS10.0热力学有限元分析实例指导手册［M］.北京:机械工业出版社，2007.