SCWCBM中钢悬臂优化设计

王 骞， 邱 文 亮， 张 哲， 张 雪 莉

（1.大连理工大学 桥梁工程研究所，辽宁 大连 116024；2.中国寰球工程公司 土建室，北京 100028）

0 引 言

混凝土箱梁正交异性钢悬臂板拓宽方法（orthotropic steel cantilever widening concrete box girder method，简称SCWCBM）是一种新型的箱梁拓宽方法.该方法不同于以往的拓宽技术，它充分利用了原有桥梁结构，无需外加桥墩，不占据桥下空间，并能保证加宽后桥梁的运营可靠性，非常适合于城市箱梁桥的拓宽［1－2］.目前SCWCBM已成功应用于大连市东北路立交桥的拓宽改造工程中［3］，运营状况良好.实际经验还表明，该方法还具有施工周期短、施工期对桥下交通干扰小等特点.

SCWCBM的特征是：在不增设桥墩的前提下，通过在混凝土箱梁两侧设置钢悬臂结构以达到拓宽原有桥梁的目的.钢悬臂结构与原有混凝土箱梁间通过横向预应力筋连成整体.新增设的钢悬臂横梁在顺桥向每隔一定长度成对地设置在原有箱梁两侧，钢悬臂横梁上铺设正交异性钢桥面板作为拓宽的行车桥面.在混凝土箱室内设置纵向体外预应力筋以增强原有混凝土梁的承载能力.

用钢悬臂梁加宽后的结构是钢－混凝土横向组合的特殊结构.新结构引出新问题，新增钢悬臂结构的设计是采用SCWCBM加宽的关键问题.本文引入拓扑优化理论以指导钢悬臂梁的外形设计，并根据平截面假定推导出横向预应力筋位置理论范围的解析表达式，最终提出新增钢悬臂结构优化设计思路.

1 SCWCBM优化设计的理论前提

SCWCBM加宽后断面形式如图1所示.

为了使采用SCWCBM加宽后的特殊结构能有效地协同工作，需协调解决两个关键问题：第一，应确保作用在钢悬臂上的荷载能有效地传向接触面；第二，确保新增的钢悬臂结构与混凝土箱梁间接触紧密且接触面混凝土不被压坏，即保证接触面上不能出现拉应力且压应力不超过接触面混凝土的抗压强度.

在钢悬臂设计过程中，本文结合上述指标，引入拓扑优化理论，结合平截面假定，提出钢悬臂优化设计思路，预先给定满足要求的参数取值建议，以此减少盲目试算次数，进行有效设计.

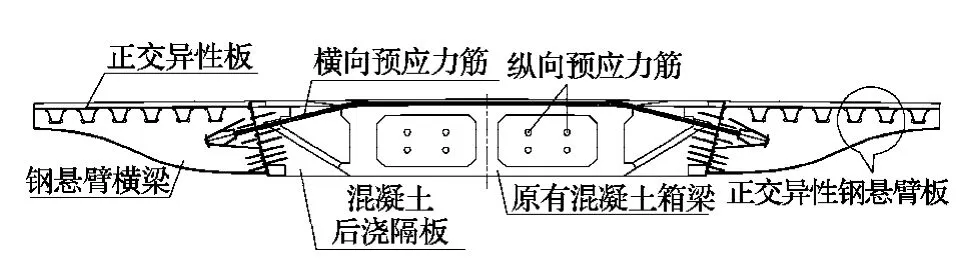
图1 采用SCWCBM加宽后的箱梁断面Fig.1 The section of box girder widened by SCWCBM

2 钢悬臂的拓扑优化设计

拓扑优化是以结构拓扑变量为分析变量，在满足已知荷载工况和约束条件的情况下，在给定的设计区域内寻求材料最优分布的过程［4］.对于试图产生超出设计者经验的新型结构，拓扑优化是一种很有价值的工具［5－6］.近年来，结构拓扑优化设计正在成为结构优化研究领域的热点.汽车、飞机制造等领域，已经开始应用拓扑优化理论进行整体的布局优化，这股热潮正在国内兴盛起来［7］，但目前应用拓扑优化进行桥梁结构设计的工程实例并不多见.采用本文所述拓宽方法加宽后的箱梁属于非常规的特殊结构，新增钢悬臂结构的拓扑造型缺少可直接利用的工程经验，本文在钢悬臂构造设计过程中引入拓扑优化设计思路，不仅为钢悬臂构造的方案设计提供了有利的指导，而且推广了拓扑优化理论在桥梁设计中的应用.

2.1 数值模型

钢－混凝土接触面为该拓宽方法的受力关键部位，在追求整个钢悬臂横梁轻质、加工便利以及外形美观的优化设计过程中，应以保证作用在钢悬臂上的汽车荷载及恒载能有效地传向接触面为前提.

如图2所示，为了保证钢悬臂横梁与原有箱梁的连接质量，在箱梁两侧后浇混凝土隔板与新增钢悬臂横梁相接触.混凝土后浇隔板也需成对设置，其数量、位置与新增钢悬臂横梁的一致［1，3］.图2中，接触面倾斜角度θ的取值应是综合考虑如下因素的结果：横向体外预应力筋的布置应与接触面垂直，体外预应力筋穿过原有箱梁时应尽量少地破坏原有结构，横向体外预应力筋的转弯半径R需满足体外预应力筋的最小规定值.综合θ取值、钢悬臂的实际加宽幅度及荷载情况建立钢悬臂优化设计的数值模型.

图2 钢－混凝土接触面构造图Fig.2 Diagram of interface between steel and concrete

初始优化区域需视原结构需拓宽的幅度和原结构的梁高而定，初始优化区域的宽度即箱梁结构需要拓宽的宽度，为了保证与原结构行车桥面一致确定优化区域高度，由图1可见新增钢悬臂结构与原有箱梁的位置关系.鉴于实际的钢悬臂横梁顶部要设置正交异性桥面板，因此在钢悬臂横梁的顶部要预留安放桥面板的U形槽.为了掌握钢悬臂横梁将所受的荷载向接触面传递的最优路径，从模型简化的角度，将钢悬臂横梁接触面的一侧视作固结.

如图3所示，预留U形槽的单端固结的结构为钢悬臂拓扑优化的基本结构.

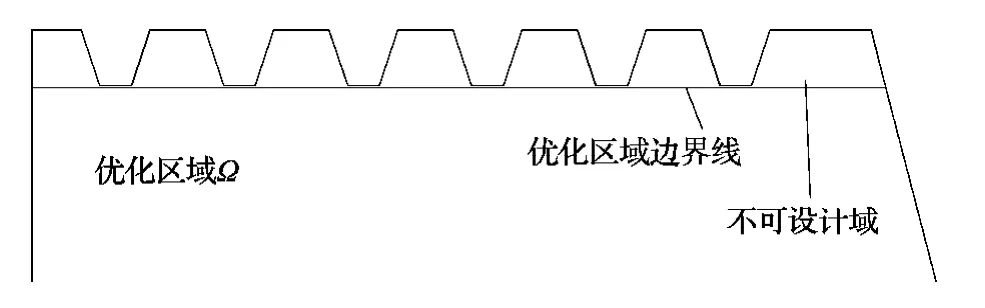
图3 实际拓扑优化结构Fig.3 Actual structure for topological optimization

作用在钢悬臂横梁上的荷载有恒载均布力以及机动车车轮荷载.恒载均布力q0为每个钢悬臂横梁均摊的正交异性桥面板及桥面铺装的恒载外力.车轮荷载按《公路桥涵设计通用规范》［8］的规定，进行最不利布载.如图4所示，以单侧加宽一个车道为例，钢悬臂加宽范围内至多可以布设两个车轮和一个车轮的局部.按照具体车辆荷载轴重及车轮作用范围可计算车轮均布荷载q1.优化分析的荷载工况一为恒载均布力q0与实际最不利车轮荷载的综合作用，如图4所示.

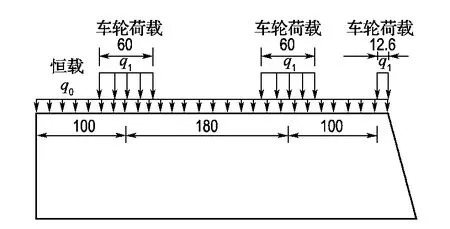
图4 工况一拓扑优化结构图（单位：cm）Fig.4 Topological optimization structure under Load Case 1（unit：cm）

车轮荷载的位置在车轮可能通行的范围内是随机的、不固定的.因此，车轮荷载除了上述最不利布载情况外，还有其他多种布载形式.为了让优化分析的结果能广泛地适用于多种车轮布载情况，这里偏保守地将车轮荷载在其可能出现的范围内满布，图5所示为荷载分析工况二的布载情况.

2.2 数学模型

本文将系统的柔度最小作为结构优化的目标函数.同样的设计区域，当边界条件及荷载一定时，系统柔度越小即代表刚度越大［5，9］.

假定作用于系统的外力为F，则系统的应变能可表示为

式中：Ω为给定设计区域；ε（u）为荷载F作用下的应变；u为设计区域内任意一点在荷载作用下的弹性变形；D为弹性矩阵；F为节点的荷载向量；U为节点的位移向量.

系统的平衡方程如下：

其中K表示系统的刚度矩阵，且KT＝K，综合式（1）、（2）可得

系统的柔度可描述为C＝FTU，对比式（1），可知系统的柔度最小等价于系统的应变能最小.

建立钢悬臂结构的拓扑优化数学模型如下.

将材料模型表示为

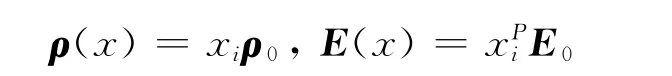
式中：ρ0和E0分别是钢悬臂板剖分后的密度和弹性矩阵；xi为单元的相对密度，P为惩罚因子.则本例中拓扑优化数学问题可被具体描述为

目标函数为

式中：单元相对密度xi为设计变量；f为体积系数.本例中的数学模型可以描述为寻找各单元的密度分布以使得整个结构的刚度最大.

拓扑优化分析过程中，除了建立合理的优化模型，尚应选择合适的优化算法，本文选用的是收敛速度较快的优化准则法［10］.

如前文所述，图3所示的实际拓扑结构的主要设计荷载工况有两种.以数学模型中目标函数刚度最大为目标，计算材料的分布情况，优化结果见图6.其中黑色区域（彩图中为蓝色）表示材料密度为0，深灰色区域（彩图中为红色）表示材料密度为1，介于中间的浅灰色区域（彩图中为黄色、绿色）属材料分布中间过渡区，材料密度介于0、1之间，处理时按照0.5处理.

将所得的拓扑结果导入CAD制图软件中，可以根据材料分布情况设计出对结构刚度损害最小的钢悬臂外形，根据工况一和工况二的拓扑结果可以大致确定钢悬臂结构的外形如图6中白色线条所示.

钢悬臂流线外形设计的前提是保证钢悬臂能将荷载有效地传递给接触面，即不破坏设计域内荷载传递路径，保证结构刚度.综合考虑工况一和工况二钢悬臂外形边界，得到钢悬臂外形设计结果如图7所示.这属于钢悬臂外形的概念设计，即初步设计.

图6 拓扑优化结果Fig．6 Topological optimization result

图7 钢悬臂设计外形Fig．7 Appearance design for steel cantilever

3 横向预应力筋位置的理论推导

3.1 基本力学模型的建立

在进行钢悬臂横梁与混凝土后浇隔板之间的界面受力分析时假设钢悬臂横梁没有弹性变形，只产生刚体移动和转动.此时混凝土界面的反力呈直线分布，如图8、9所示.

如前文所述，确保加宽后的特殊结构协同工作的另一关键问题就是要使新增的钢悬臂结构与混凝土箱梁间接触紧密且接触面混凝土不被压坏，即保证接触面上不能出现拉应力且压应力不超过接触面混凝土的抗压强度容许值.

图8 钢－混凝土接触面力学模型一Fig.8 Mechanical model one of steel－concrete interface

图9 钢－混凝土接触面力学模型二Fig.9 Mechanical model two of steel－concrete interface

分析实际工程情况，从施工阶段到使用阶段，钢－混凝土接触面的应力分布有两个临界工况.临界工况一：当钢悬臂横梁安装就位、横向预应力筋张拉完毕且正交异性桥面板及桥面铺装施工之前，预应力荷载起主要作用，该阶段钢－混凝土接触面上缘压应力最大，下缘应力最小；临界工况二：当正交异性桥面板安装完毕，桥面铺装就位后，在使用过程中，当车轮荷载位于横向最不利布载位置时（参见图4），钢－混凝土接触面的上缘应力最小，而下缘应力最大.保证这两种临界工况下接触面的上、下缘均不出现拉应力，且压应力不超过接触面混凝土的抗压强度容许值便可保证其他荷载工况下接触面的应力分布满足要求.

3.2 横向预应力筋作用位置的理论推导

3.2.1 临界工况一受力分析 该工况只有钢悬臂横梁的自重和体外预应力筋作用，假定O为弯曲中心，将钢悬臂横梁的自重简化为通过弯曲中心的集中力P0和弯矩M0，横向体外预应力为F，其作用位置距离弯曲中心的距离为x1；接触面长度为l，截面上缘距离弯曲中心的距离为x0，接触面下缘距离弯曲中心的距离为l－x0；接触面上缘的反力为q1，接触面下缘的反力为q2，钢材的弹性模量远大于混凝土的弹性模量，因此文中假定接触面上应力呈线性分布.临界工况一的力学模型如图8所示.

由图8有

由式（7）有

为保证钢悬臂横梁与混凝土后浇隔板间良好的界面联系，应满足接触面下缘不出现拉应力且上缘的压应力不超过接触面混凝土的抗压强度容许值［σ］.因此需满足q1≤［σ］t，t为截面下缘混凝土后浇隔板的宽度，同时应满足q2≥0.

式（9）结合上述安全要求，则有

由q1≤ ［σ］t，且

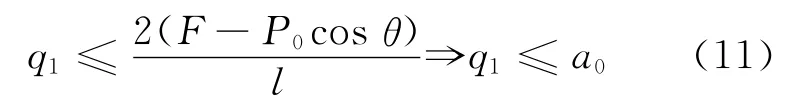
由q2≥0，且

其中

再由式（8），取x0＝l／2，得到

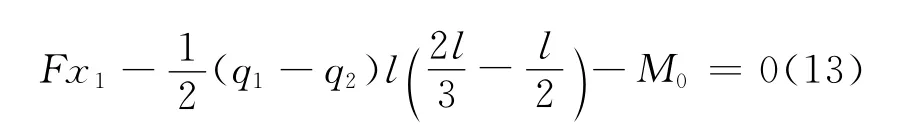
将式（9）代入式（13）有

由式（11）、（14）得6（Fx1－M0）／l2＋ （FP0cosθ）／l≤a0，即

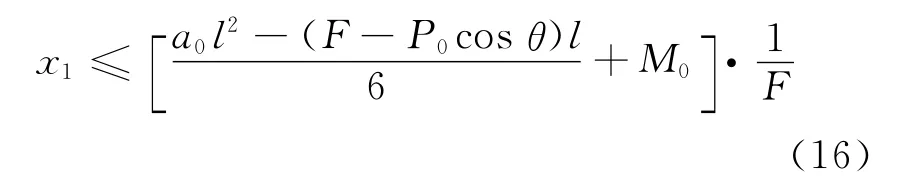
由式（12）、（15）得（F－P0cosθ）／l－6（Fx1－M0）／l2≥b0，即

综合式（16）及式（17），x1取值有上限：

3.2.2 临界工况二受力分析 将作用于钢悬臂横梁上的恒载及车轮荷载简化为通过接触面弯曲中心O的集中力P和弯矩M，横向体外预应力为F，其作用位置距离弯曲中心的距离为x1，基础面长度为l，截面上缘距离弯曲中心的距离为x0，接触面下缘距离弯曲中心的距离为l－x0；接触面上缘的反力为q1，接触面下缘的反力为q2，仍假定接触面上应力呈线性分布.临界工况二的力学模型如图9所示.

由图9有

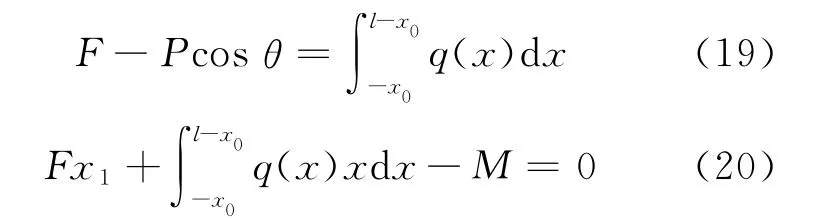
沿x轴方向由摩擦力平衡应有

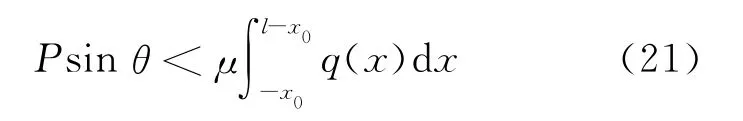
由式（19）、（21）有Psinθ＜μ（F－Pcosθ），因此体外预应力F取值有下限：

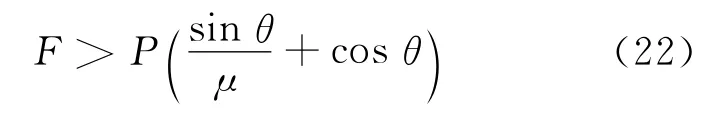
为保证工况二钢悬臂横梁与混凝土后浇隔板间良好的界面联系，应满足接触面上缘不出现拉应力且下缘的压应力不超过接触面混凝土的抗压强度容许值.因此需满足q1≥0，同时应满足q2≤［σ］t，t为截面下缘混凝土后浇隔板的宽度.

参照临界工况一推导过程，得x1取值有下限：

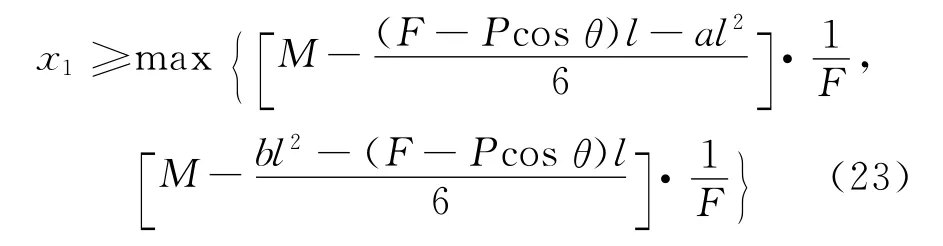
3.2.3 横向预应力筋作用位置及体外预应力取值 综合式（18）、（23），横向预应力筋作用位置x1的理论取值范围如下式所示：

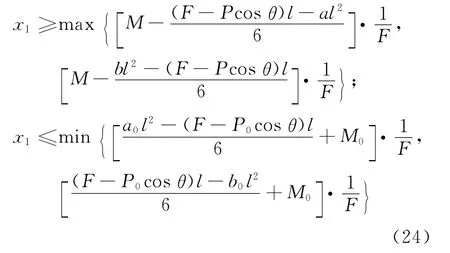
合理的F、x1取值是保证接触面受力满足要求的重要前提.综上所述，在进行SCWCBM横向体外预应力筋设计时，需以式（10）为参照，根据式（10）可确定横向体外预应力F的取值界限，在此范围内设定预应力筋的型号、根数，确定F值，再由式（24），计算求得x1的取值范围，即横向体外预应力筋作用位置的理论范围.调节F值，至横向预应力筋作用位置合理可行为止.

4 钢悬臂优化设计思路

综合钢悬臂拓扑优化设计及横向预应力筋位置的理论推导结果，提出混凝土箱梁正交异性钢悬臂板拓宽方法中的钢悬臂部分优化设计思路：首先对设定区域进行拓扑优化计算，根据优化结果设计钢悬臂横梁的外形；在此外形的基础上结合实际工程的两种临界工况推导出横向体外预应力的取值界限及横向预应力筋合理作用范围；选取合适的F值，确保横向体外预应力筋的位置合理可行；随后进行钢悬臂横梁接触面附近加劲肋的细部设计；最后对临界工况下钢－混凝土接触面的接触应力进行有限元精确分析，验证各设计参数的取值是否合理.按照该优化设计思路进行的SCWCBM钢悬臂优化设计可以有效减少试算次数，节约计算资源.

5 工程应用

大连市东北路立交桥拓宽改造工程采用该优化设计思路进行钢悬臂设计，确定的钢悬臂横梁外形尺寸及横向预应力筋位置能够确保接触面应力满足要求［11］，并通过足尺模型试验验证了数值模拟结果的正确性［1］，表明该钢悬臂优化设计思路是合理可行的.

6 结 论

（1）在钢悬臂梁构造设计过程中，引入拓扑优化理论，构建钢悬臂结构的数学模型，选定合适的优化算法，优化迭代求得设计区域内合理的材料分布结果.该拓扑结果可为SCWCBM钢悬臂梁的外形设计提供理论依据.

（2）进行了钢悬臂横梁与混凝土后浇隔板之间的界面受力分析.为保证任何荷载工况下接触面上不出现拉应力，且压应力不超过后浇隔板混凝土的抗压强度容许值，创建了两种临界荷载工况下的钢悬臂梁的基本力学模型，根据平截面假定推导出横向预应力筋理论作用范围的解析表达式.

（3）给出基于钢－混凝土接触面受力问题的优化设计思路.采用该优化设计思路进行SCWCBM钢悬臂优化设计可以减少不必要的试算次数，极大限度地节约计算资源，达到快速准确设计的目的.该设计思路和方法为SCWCBM的推广提供了理论支持.

［1］WANG Qian，SHI Lei，ZHANG Zhe.A new widening method of reinforced concrete box girder and its experimental research ［C］／／ Advanced Materials Research.Switzerland：Trans Tech Publications Ltd.，2011：3724－3729.

［2］WANG Qian，ZHANG Zhe.Orthotropic steel cantilever widening method of concrete box girder［J］.Structural Engineering International，2011，21（2）：228－231.

［3］WANG Qian，SHI Lei，ZHANG Zhe.Application of a new kind of widening method in Dalian Northeast Road overpass improvement project［C］／／ Proceedings of the 9th International Conference on Civil and Environmental Engineering.Beijing：China Architecture ＆Building Press，2010.

［4］谢 涛，刘 静，刘军考.结构拓扑优化综述［J］.机械工程师，2006（8）：22－25.XIE Tao，LIU Jing，LIU Jun－kao.An overview on the topological optimization of structures ［J］.Mechanical Engineer，2006（8）：22－25.（in Chinese）

［5］杨贵玉.拓扑优化方法及其在微型柔性机构设计中应用的研究［D］.大连：大连理工大学，2004.YANG Gui－yu.Research on the method of topology optimization and its application in design of MEMS compliant mechanism［D］.Dalian：Dalian University of Technology，2004.（in Chinese）

［6］邵新妍，逢毓卓.浅谈结构拓扑优化设计［J］.科技咨询导报，2007（3）：24－25.SHAO Xin－yan，FENG Yu－zhuo.Discussion on topological optimization design ［J］.Science and Technology Consulting Herald，2007（3）：24－25.（in Chinese）

［7］穆春燕.拓扑优化理论及其在拱坝优化设计中的应用［D］.南京：河海大学，2006.MU Chun－yan.Topology optimum design theoryand its application on optimization design of arch dam ［D］.Nanjing：Hohai University，2006.（in Chinese）

［8］中交公路规划设计院.JTG D60—2004公路桥涵设计通用规范［S］.北京：人民交通出版社，2004.CCCC Highway Consultants Co.，Ltd..JTG D60－2004General Code For Design of Highway Bridges and Culverts［S］.Beijing：China Communication Press，2004.（in Chinese）

［9］朱灯林，陈俊伟，俞 洁，等.结构拓扑优化设计的研究现状及其应用［J］.机械制造与自动化，2005，36（6）：7－11.ZHU Deng－lin，CHEN Jun－wei，YU Jie，etal.Developments of structural topology design and its application in structural design ［J］.Machine Building ＆ Automation，2005，36（6）：7－11.（in Chinese）

［10］Rozvany G，ZHOU M.The COC algorithm，PartⅠ：Cross－section optimization or sizing ［J］.Computer Methods in Applied Mechanics and Engineering，1991，89（11）：281－308.

［11］WANG Qian，QIU Wen－liang，LI Fei－ran，etal.Contact stress analysis of steel concrete box girder widened by orthotropic steel cantilever ［C］／／Proceeding of the 10th International Conference on Civil and Environmental Engineering.Taiwan：National Central University，2011.