随机双指数记忆耗散系统的非马尔可夫扩散*

谢文贤 许鹏飞 蔡力 李东平

(西北工业大学应用数学系,西安 710072)

(2012年11月26日收到;2012年12月12日收到修改稿)

1 引言

众所周知,广义朗之万方程(generalized Langevin equation,GLE)是描述反常扩散的主要途径之一[1-5].大量研究表明,在幂函数型[6,7]、指数型[6,8]、双指数型记忆核函数[9-11]中均观察到不同类的反常扩散现象.Wang等[3,12]建立了GLE所对应的反常扩散及其福克-普朗克(Fokker-Planck)方程与概率密度函数之间的关系.Porr`a等[6]针对GLE在耗散记忆核函数与噪声相关函数变化的情况下,研究了粒子运动由平稳状态到超扩散的演化趋势,随着参数的变化呈现出了欠扩散、正常扩散等现象.Bao等[4,13,14]基于GLE针对简谐速度噪声(harmonic-velocity noise)深入研究了反常扩散下的动力学等问题.Vi˜nales等[7,15]则围绕Mittag-Leffl er噪声和长时拖尾噪声(long-time tail noise)研究了GLE带有简谐振子的反常扩散现象,大大深化了随机环境对扩散现象的影响.除反常扩散一系列研究外,此领域还涉及GLE的数值模拟[11,16]、遍历性[17]、随机共振[18-20]等的研究.

上述研究结果多限于单自由度耗散系统,而关于多自由度情形涉及较少.多自由度情形中不容忽视的问题就是不同噪声源的互关联性[21-28].以往诸多研究表明互关联性对随机共振[22-24]、平均首次穿越[26,27]等现象影响深刻.近来,Wang等[28]在互关联噪声激励的两自由度耦合系统(可用GLEs表示)中,细致分析了含有幂函数型的记忆核情形下的反常扩散问题.而Roy等[29]和Kumar[30]应用具有耦合阻尼项的两自由度耗散系统来研究电子受垂直于相平面方向的均匀磁场作用下的轨道磁力矩的特性.但是此类系统的扩散问题笔者目前尚未见报道.鉴于此,本文将其GLEs推广至互关联情形,研究具有双指数记忆核函数和阻尼耦合的系统的响应二阶矩所呈现出的非马尔可夫扩散行为,并分析不同噪声源间的互关联性对其影响.具体的GLEs如下：

其中粒子质量为m,阻尼耦合因子为B.内噪声ξi(t)满足 〈ξi(t)〉=0,以及涨落耗散定理 〈ξi(t)ξj(t′)〉=kBTβij(|t-t′|)(i=x,y),kB为 Boltzmann 常数,T 为环境的绝对温度.

方程(1)也可视为一般机械振动理论中具有耦合黏性阻尼B的运动方程的推广.

2 热宽带噪声激励下的系统响应矩

2.1 两噪声不存在互关联的情形

首先考虑系统(1)的双指数记忆核函数(i=x,y),其满足

其中τ1和τ2为两个相关时间,β0为摩擦系数.此时,两噪声不存在互关联性,系统(1)退化为具有耦合阻尼项的GLEs.不失一般性,令m=1,引入新变量x˙(t)=v(t),y˙(t)=u(t),并运用Laplace变换,易得系统(1)的位移x(t),y(t)和速度v(t),u(t)的表达式

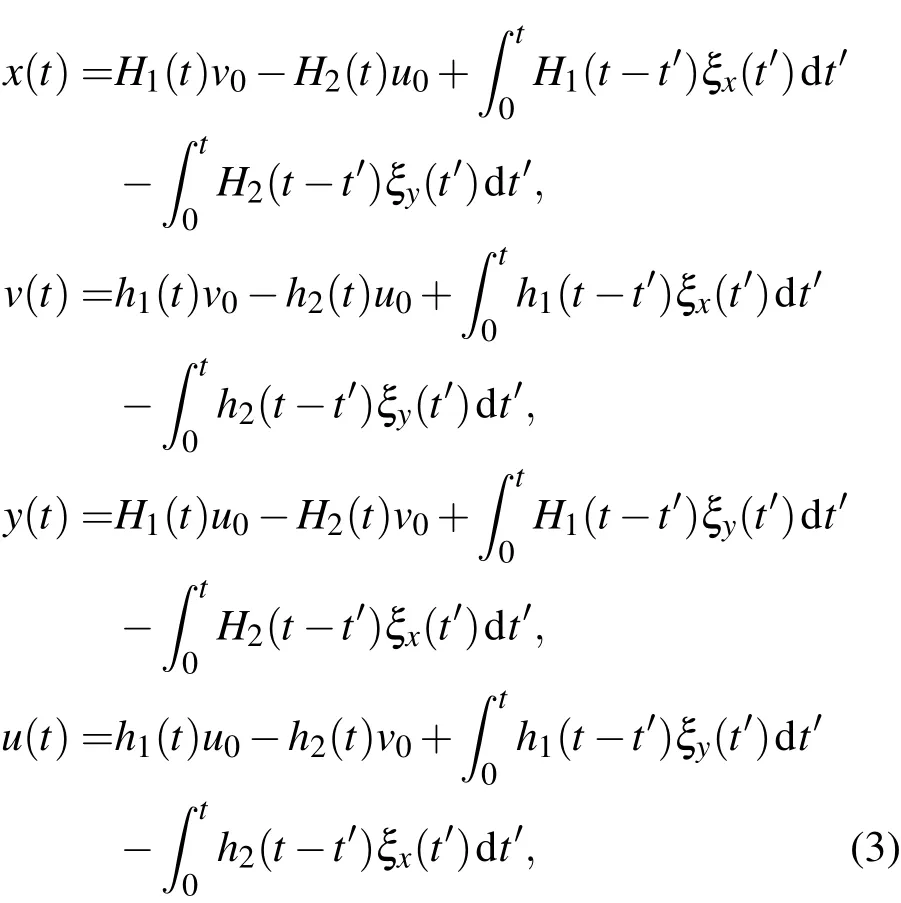
其中,取初始位移x0=y0=0及初始速度v0=1.2,u0=0.8,而 βxx(t),hi(t),Hi(t)分别为对应于 βˆxx(s),hˆi(s),Hˆi(s)的逆Laplace变换(i=1,2).这里

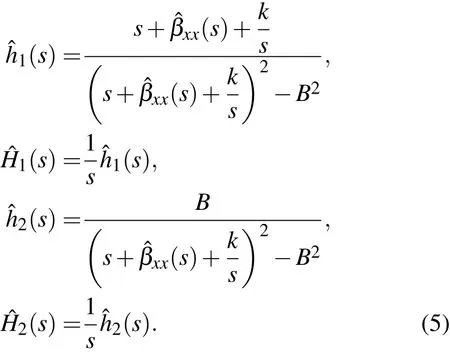
结合(2)—(5)式,并运用Laplace变换可得系统响应二阶矩的表达式

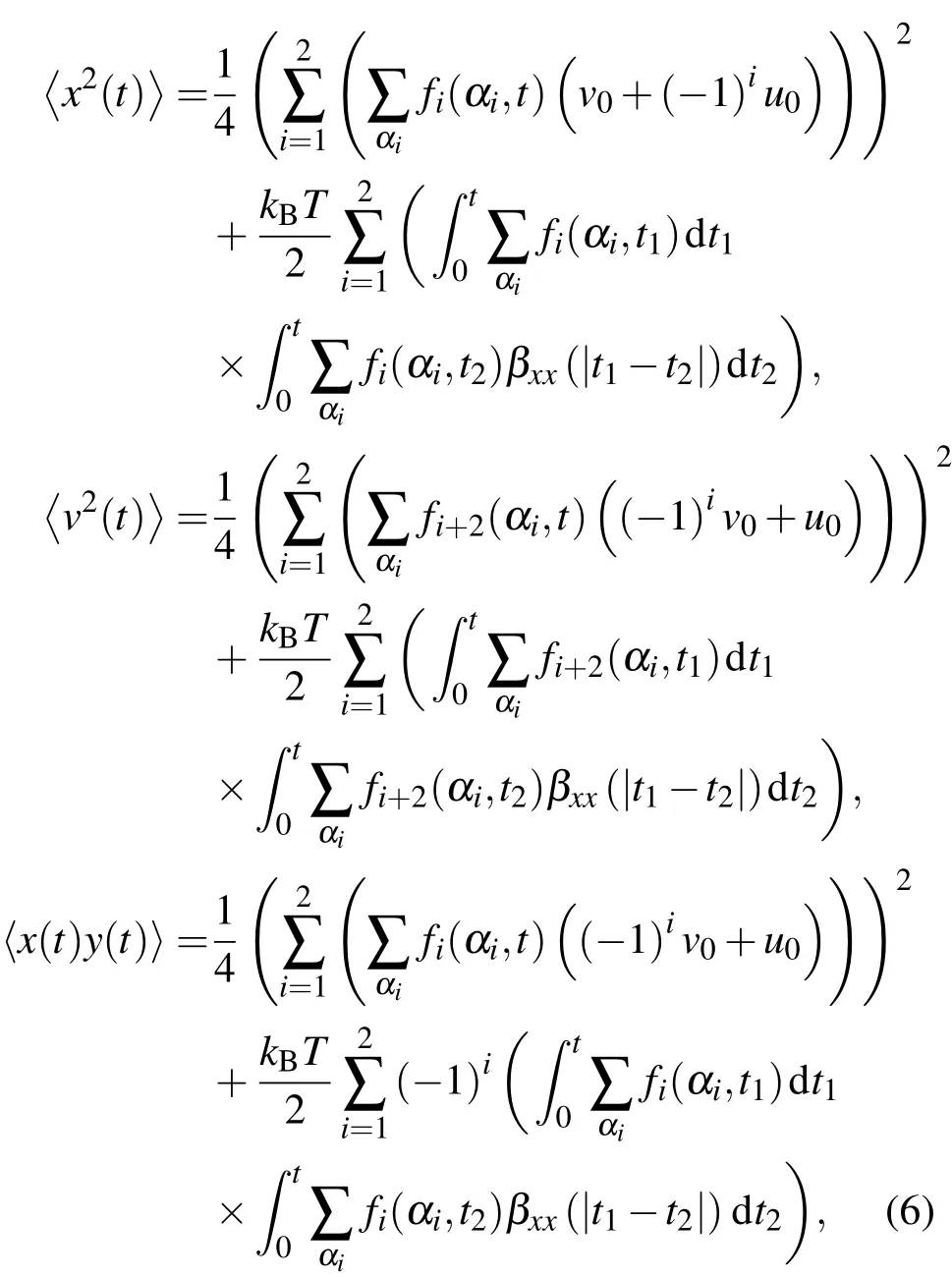
其中αi为如下方程di(z)=0的根(i=1,2)：

由于系统(1)的对称性,位移y(t)和速度u(t)的二阶矩与(6)式结构类似.

特别地,当相关时间τ1→∞,则ξi(t)(i=x,y)退化为Ornstein-Uhlenbeck噪声,文献[6,8]对此类单自由度系统的反常扩散的研究已有报道.进一步,当相关时间τ2→0,则ξi(t)(i=x,y)退化为高斯白噪声,系统(1)的耗散记忆核函数失效,表现为马尔可夫性;其位移二阶矩是正常扩散的.为了具体分析噪声性质和耗散性质对扩散现象的影响,以下讨论中均选定参数值kBT=5.0,k=1.0.

图1和图2中给出位移二阶矩〈x2(t)〉随时间t的非马尔可夫振荡扩散.热宽带噪声仅在其相关时间τ2充分小时退化为“绿”噪声[11].在“绿”噪声范围内,〈x2(t)〉随着相关时间τ1的增大而递增,但相关时间τ1增加到一定程度时,〈x2(t)〉随τ1的增加其变化减弱.图1中τ1=10与τ1=15所对应的〈x2(t)〉非常接近,这表明τ1增加到一定程度时,“绿”噪声逐渐退化成高斯白噪声,即有此时，结合(4)—(6)式可得高斯白噪声激励下位移二阶矩：

其中

当系统参数k=B=0时,系统(1)退化为无简谐势束缚的单自由度系统,此时,位移二阶矩〈x2(t)〉在“绿”噪声范围内将退化为弹道扩散[9].图2分析了(2)式中摩擦系数β0对位移二阶矩〈x2(t)〉的影响.当摩擦系数 β0=0.01 时,〈x2(t)〉呈现振荡形式的扩散,并且振荡幅度随着时间的演化逐渐增大.而随着摩擦系数β0的不断增大,系统阻尼使粒子运动减弱,〈x2(t)〉明显趋于平稳状态,即符合物理直观.

图 1 〈x2(t)〉作为t的函数随τ1变化的曲线 (B=0.05,β0=0.01)

图2 〈x2(t)〉作为t的函数随 β0变化的曲线 (τ1=7,τ2=3,B=0.05)

2.2 两噪声互关联的情形

若考虑两噪声色相关的情形：

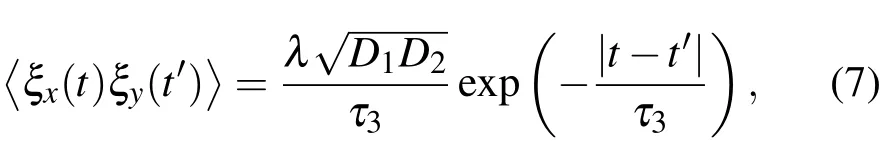
其中D1和D2分别表示两激励噪声的强度(D1=λ 为互关联强度,τ3为互关联时间.若τ3→0,则(7)式退化为白关联情形

考虑到两噪声所满足涨落耗散定理,可得系统(1)中记忆核函数

类似(4)和(5)式,导出βxy(t),gi(t),Gi(t)(i=1,2)的Laplace变换如下：

结合(4),(7),(9)—(11)式,可得系统(1)各响应的二阶矩.这里仅列出〈x2(t)〉的表达式：

其中αi为如下方程wi(z)=0的根(i=1,2)：

图3描述了粒子沿着x轴方向的位移二阶矩〈x2(t)〉随耦合因子B的变化情况,在短时间内影响不显著,但长时间后随着B的增加而其扩散加剧.在两噪声存在互关联(λ=1)情形时,图3中虚线表明〈x2(t)〉仍呈现振荡扩散,且耦合因子B同样将促进〈x2(t)〉的扩散.相较于无关联(λ=0)情形(实线),互关联情形的扩散加剧.

图3 两噪声有(无)互关联情形下〈x2(t)〉作为t的函数随B变化的曲线 (τ1=7,τ2=3,β0=0.05)

图4 〈x2(t)〉作为t的函数随B和λ变化的曲线(τ1=7,τ2=3,β0=0.05)

图4 描述了系统(1)的位移二阶矩〈x2(t)〉在阻尼耦合因子B=0时随时间t的变化情况.当两噪声无关联(λ=0)时,系统退化为仅受简谐势场束缚的单自由度系统,此时,〈x2(t)〉在长时间后趋于平稳状态,即 〈x2(∞)〉=kBT/k.而在两噪声互关联(λ=1,τ3=4.5)时,系统(1)退化为仅受二维简谐势场束缚的两自由度系统,互关联性延长了〈x2(t)〉的弛豫时间.

结合图3和图4,在两噪声有(无)关联情形下,耦合因子B将使得粒子远离简谐势场的束缚,而呈现普遍的振荡扩散.

图5 〈x2(t)〉作为 τ3的函数随 λ 变化的曲线(τ1=7,τ2=3,B=0.05,β0=0.3,t=30)

图6 〈x(t)y(t)〉作为t的函数随τ3和λ变化的曲线(τ1=10,τ2=0.01,B=0.02,β0=0.3)

图5 描述了位移二阶矩〈x2(t)〉(12)式作为互关联时间τ3的函数,随着两噪声间的互关联强度λ变化情况.〈x2(t)〉随着τ3的增加而单调递减,突显了色关联性(7)式演化为白关联性(8)式时,〈x2(t)〉的扩散得到显著加剧.〈x2(t)〉随着互关联强度λ的增加而增大,即两个色噪声之间的互关联性越强,位移二阶矩扩散就越强.图6表明,色关联性(7)式延缓〈x(t)y(t)〉趋于平稳状态的趋势,τ3越小其负相关性越强,弛豫时间越长.

3 结论

本文导出了(互关联)热宽带噪声激励的具有耦合阻尼项的系统(1)响应二阶矩的解析表达式,并讨论了〈x2(t)〉和〈x(t)y(t)〉随各系统参数的变化情况.粒子在简谐势场中受阻尼耦合因子B的作用,位移二阶矩〈x2(t)〉出现了普遍振荡式的非马尔可夫扩散,其在一定范围内随噪声相关时间τ1和耦合因子B的增大而扩散加剧,耗散记忆核函数的摩擦系数不断增大将使〈x2(t)〉呈现平稳状态.而两热宽带噪声之间的互关联性对响应二阶矩起着十分显著的影响：互关联强度对〈x2(t)〉的非马尔可夫扩散呈现促进作用,并加强了两位移间的互相关性;相反,较大的互关联时间却抑制〈x2(t)〉扩散和位移间相关性的加强.上述二阶矩特性将有助于系统(1)的随机共振及遍历性的讨论.

[1]Bao JD 2005 Progress Phys.25 359(in Chinese)[包景东2005物理学进展25 359]

[2]Zhuo Y Z 2004 Nuclear Phys.Rev.21 83(in Chinese)[卓益忠2004原子核物理评论21 83]

[3]Wang K G,Tokuyama M 1999 Physica A 265 341

[4]Bao JD,Zhou Y,L¨u K 2006 Phys.Rev.E 74 041125

[5]Siegle P,Goychuk I,H¨anggi P2010 Phys.Rev.Lett.105 100602

[6]Porr´a JM,Wang K G,Masoliver J1996 Phys.Rev.E 53 5872

[7]Vi˜nales A D,Desp´osito M A 2006 Phys.Rev.E 73 016111

[8]Bao JD,Bai ZW 2005 Chin.Phys.Lett.22 1845

[9]Bao JD,Zhuo Y Z 2003 Phys.Rev.Lett.91 138104

[10]Siegle P,Goychuk I,Talkner P,H¨anggi P2010 Phys.Rev.E 81 011136

[11]Bao JD 2004 J.Stat.Phys.114 503

[12]Wang K G 1992 Phys.Rev.A 45 833

[13]Bao JD,Song Y L,Ji Q,Zhuo Y Z 2005 Phys.Rev.E 72 011113

[14]Bao JD,Zhuo Y Z,Oliveira F A,H¨anggi P 2006 Phys.Rev.E 74 061111

[15]Vi˜nales A D,Wang K G,Desp´osito M A 2009 Phys.Rev.E 80 011101

[16]L¨u K,Bao JD 2005 Phys.Rev.E 72 067701

[17]Plyukhin A V 2011 Phys.Rev.E 83 062102

[18]Neiman A,Sung W 1996 Phys.Lett.A 223 341

[19]Bai WSM,Peng H,Tu Z,Ma H 2012 Acta Phys.Sin.61 210501(in Chinese)[白文斯密,彭皓,屠浙,马洪2012物理学报61 210501]

[20]Zhong SC,Gao SL,Wei K,Ma H 2012 Acta Phys.Sin.61 170501(in Chinese)[钟苏川,高仕龙,韦鹍,马洪2012物理学报61 170501]

[21]Xu W,Jin Y F,Xu M,Li W 2005Acta Phys.Sin.54 5027(in Chinese)[徐伟,靳艳飞,徐猛,李伟2005物理学报54 5027]

[22]Jin Y F,Hu H Y 2009 Acta Phys.Sin.58 2895(in Chinese)[靳艳飞,胡海岩2009物理学报58 2895]

[23]Jin Y F 2012 Physica A 391 1928

[24]Zeng CH,Wang H,Wang H T 2011 Chin.Phys.B 20 050502

[25]Fuli´nski A,Telejko T 1991 Phys.Lett.A 152 11

[26]Zhang N M,Xu W,Wang C Q 2007 Acta Phys.Sin.56 5083(in Chinese)[张娜敏,徐伟,王朝庆2007物理学报56 5083]

[27]Jiang L L,Luo X Q,Wu D,Zhu SQ 2012 Chin.Phys.B 21 090503

[28]Wang Y X,Zhao NR,Yan Y J2012 Phys.Rev.E 85 041142

[29]Roy D,Kumar N 2008 Phys.Rev.E 78 052102

[30]Kumar N 2012 Phys.Rev.E 85 011114