光场位相算符和逆算符的Weyl编序展开*
李学超 杨阳 范洪义
1)(安徽理工大学理学院,淮南 232001)
2)(中国科学技术大学近代物理系,合肥 230026)
3)(中国科学技术大学材料科学与工程系,合肥 230026)
(2012年9月2日收到;2012年12月26日收到修改稿)
1 引言
自从1927年Dirac[1]首次通过光子湮灭算符引入位相算符以来,在量子光学中它一直是个重要的课题.在量子力学中位相算符可以反映量子态的位相性质,Dirac通过极分解a=·S(S为位相算符)定义位相算符,这里N=a†a是[粒子]数算符,a†(a)分别是玻色产生 (湮灭)算符,a,a†=1.随后Carruthers等[2]修正了位相算符,把它定义为

那么位相算符的经典对应是什么?这个问题的解决在以往的文献中尚未见有讨论,原因可能是位相算符是非线性的.本文通过推导位相算符的Weyl编序来研究它及其经典对应,在此基础上研究产生算符和湮灭算符的逆的Weyl编序.这是深入了解光场算符性质的一种新的途径.
在粒子数表象|n〉中,利用


得到位相算符在粒子数表象中展开
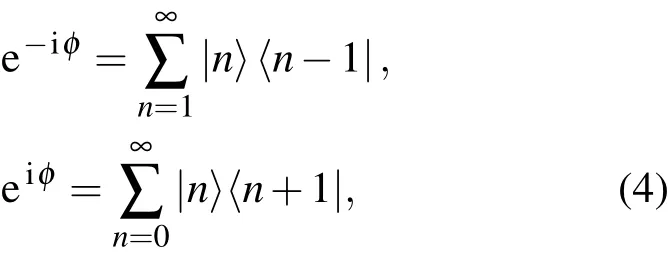

注意到|0〉是真空态,a|0〉=0,可见 eiφ与 e-iφ是不对易的.
在量子光学中,人们经常会将算符在不同的表象中展开,如P表示,Q表示以及密度算符的Wigner函数[3-6]等.算符A的Q表示可以简单地利用粒子数表象来获得:
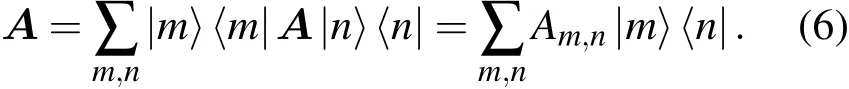
在以往的文献中,方程(6)除了提示我们求矩阵元Am,n外,并没有提供过多的信息,|m〉〈n|被认定是这种展开的一个“终极的”表示.本文将突破|m〉〈n|这个“终极的”表式,用算符的Weyl编序理论对上式继续推导,将A以Weyl编序展开[7].利用Weyl编序算符在相似变换下的序不变的优点,不仅可以获得关于光场算符的一些新的信息,同时也推导出许多有用的积分公式和一些特殊函数的生成函数,尤其是导出带负幂次的复高斯积分公式.
2 |m>文献[8]曾导出任意一个算符的Weyl编序形式的公式
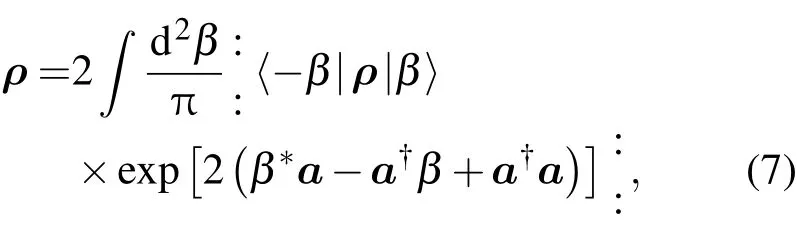

可见(7)式是正确的.由

并且利用双变量厄米特多项式的积分与表示

这里
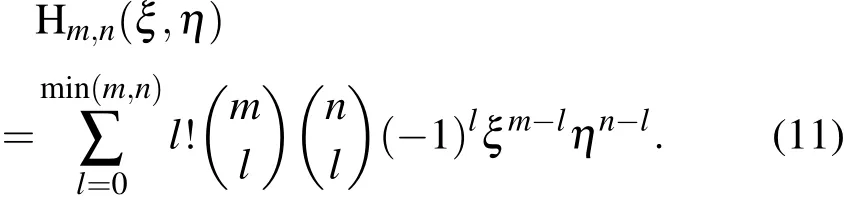
我们就可用有序算符内的积分技术[9-12]来推导出|m〉〈n|的 Weyl编序式
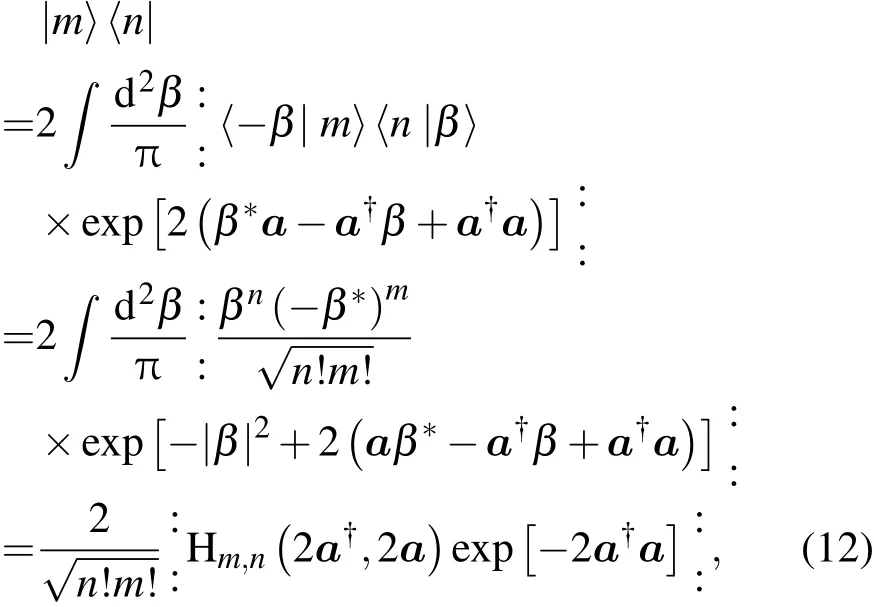
将上式代入(7)式,即可得到任一算符用双变量的厄米特多项式展开的新形式

3 光场位相算符的经典对应
作为(13)式的应用,我们来推导位相算符的Weyl编序.利用

将其代入(13)式,得到

根据Weyl量子化理论[7],位相算符 e-iφ的Weyl对应式为

由于Wigner算符Δ(α)的Weyl编序为[13]

所以对照(15)式可见

这说明位相算符的经典对应是
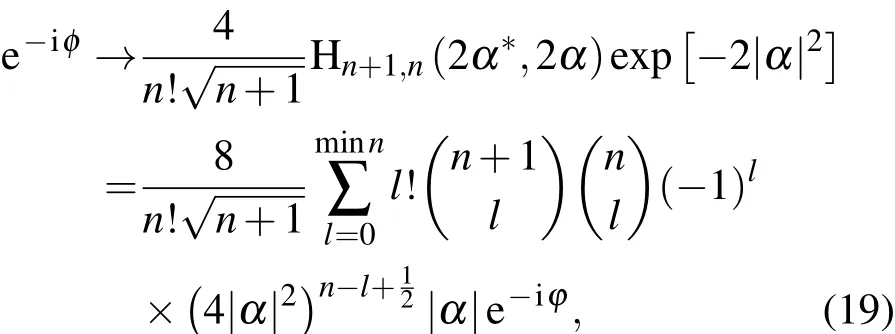
可见位相算符 e-iφ对应的经典位相体现在 eiφ,
同样我们也可以算出 eiφ的Weyl编序式
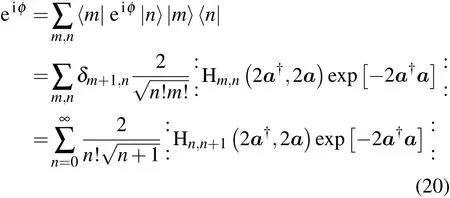
所以算符 eiφ的经典对应为
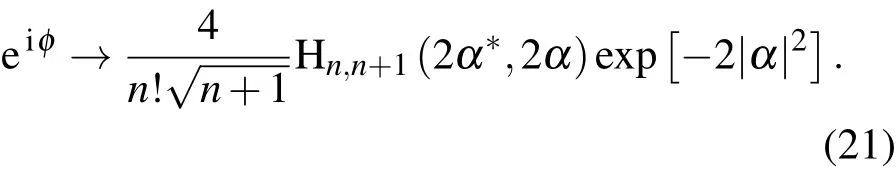
4 产生算符和湮灭算符的逆的Weyl编序式及应用
Dirac[14]首先考虑了湮灭算符的逆a-1.既然产生算符描述光子产生过程,产生算符的逆应该描写光子湮灭过程;反之,湮灭算符的逆应该描写产生过程.但要注意由于a|0〉=0,尽管aa-1=1,但a-1a/=1.用相干态和围道积分的方法[15]可以将粒子数态|n〉表示为
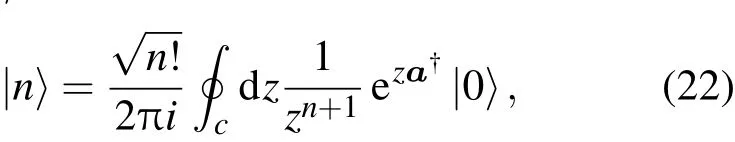
这里的围道C包括了z=0点,在围道积分下a-1e z a†|0〉=z-1ez a†|0〉就有了意义,于是有
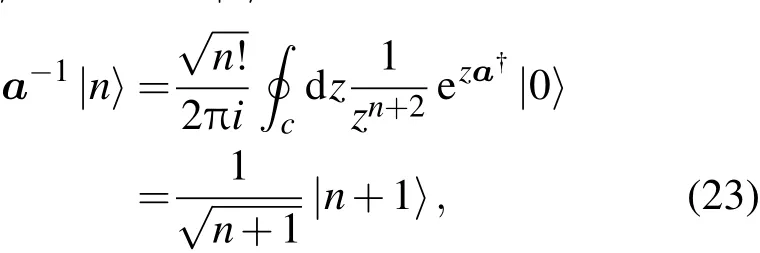
即

a-1满足

利用(24)式得到

将
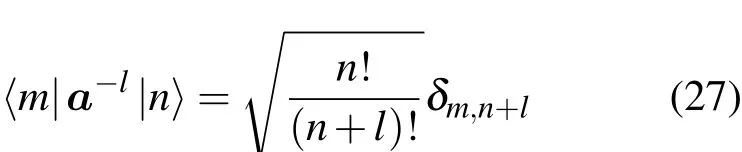
代入(13)式得到
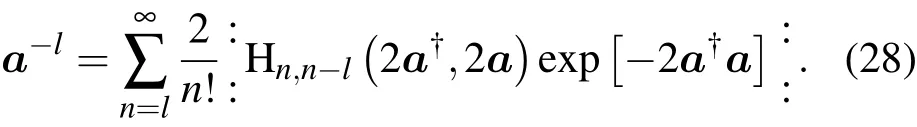
另一方面,直接利用(7)式又有

该式代入时利用了 a-1|β〉=β-1|β〉,比较 (28)和(29)两式得到

由于Weyl编序中,产生算符与湮灭算符是可交换的,可以将其看作积分参量,从(30)式得到一个新的积分公式

注意β-l是负幂次,所以这个积分带有瑕点,不易用常规的方法积分,这里用Weyl编序方法绕过了这一困难.()
同样我们可以推导出a†-l的Weyl编序
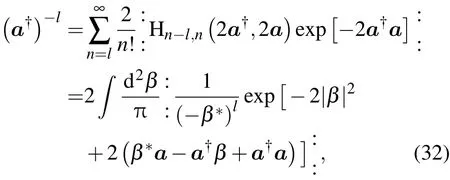
由此可以悟出带负幂次(β∗)-l的新高斯积分公式

进一步由(24)式可见

将

代入(13)式得
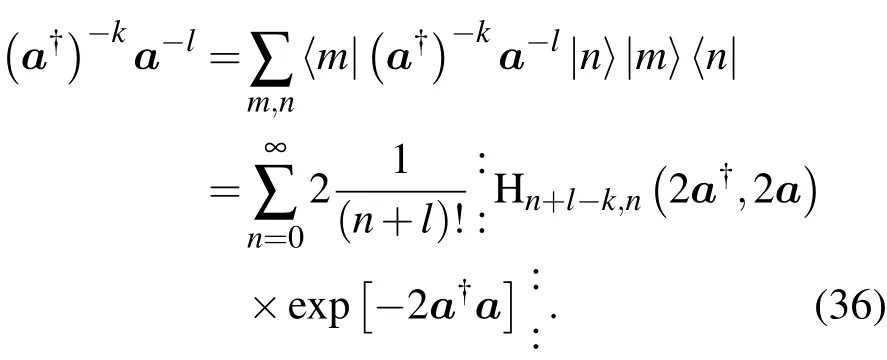
另一方面,直接利用(7)式又得到

比较以上两式,可以悟出关于带负幂次(β∗)-kβ-l的新高∫斯 积分公式

进一步可改写为
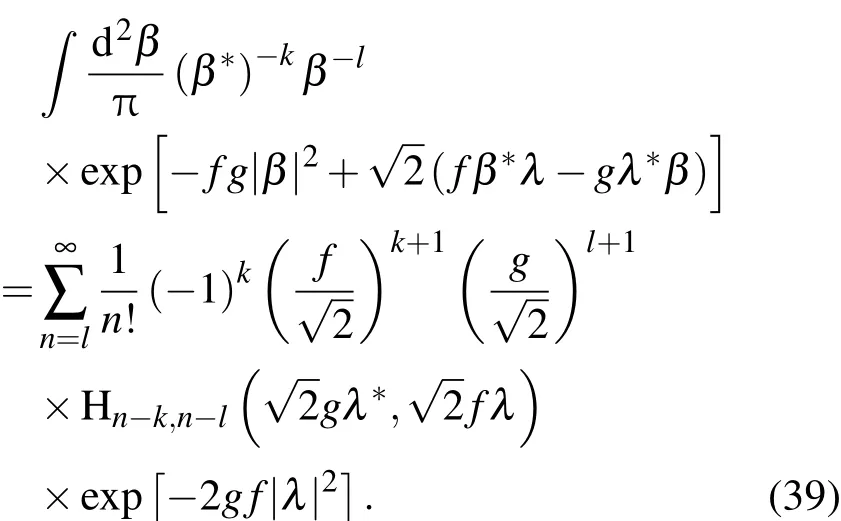
作为比较,我们推导带正幂次(β∗)kβl的新高斯积分公式.将


另一方面,将(a†)kal直接代入(7)式得
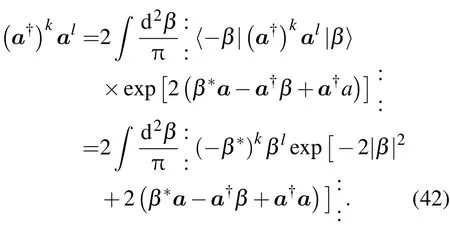
比较以上两式,可以悟出关于带正幂次(β∗)kβl的新积分公式
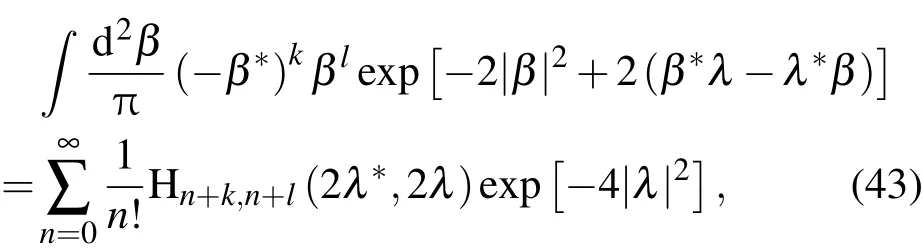
另一方面利用(10)式得到
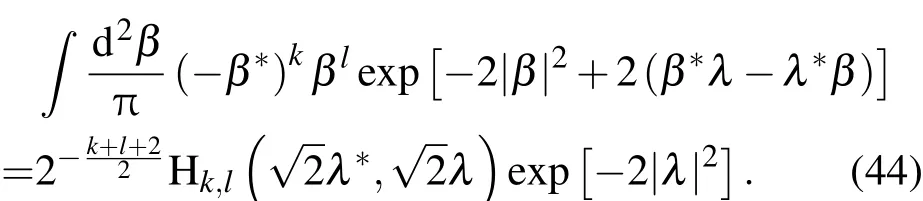
比较(44)与(45)式,得出关于双变量厄米特多项式的一个新的母函数公式
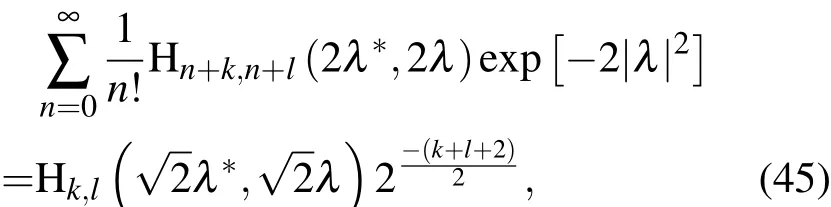
该式也可利用其他方法验证.
(45)式进一步可改写为
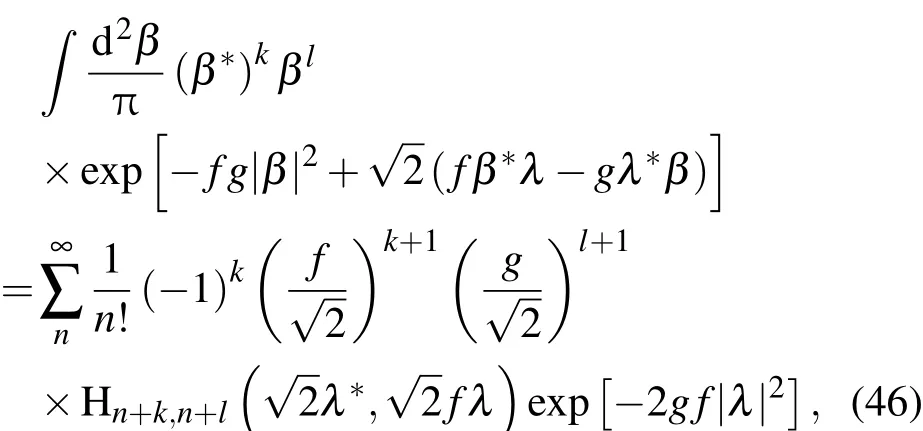
该式正好与(41)式相匹配.
5 结论
本文推导出了光场位相算符的Weyl编序,写出了其经典对应,这对于深入了解光场算符的性质提供了一种新的途径;推导了产生算符与湮灭算符的逆的Weyl编序,并据此推导出了某些特殊函数的新的生成函数和带负次幂的高斯积分公式.
[1]Dirac PA M 1927 Proc.R.Soc.London A 114 243
[2]Carruthers P,Nieto M M 1968 Rev.Mod.Phys.40 411
[3]Wigner EP1932 Phys.Rev.40 749
[4]Klauder JR,Skagerstam B S1985 Coherent States(Singerpore:World Scientifi c Publishing)
[5]Scully M O,Zubairy M S 1997 Quantum Optics(United Kingdom:Cambridge University Press)
[6]Glauber RJ1963 Phys.Rev.130 2529
[7]Weyl H 1927 Z.Phys.A 46 1
[8]Fan HY 1992 J.Phys.A 25 3443
[9]Fan H Y,Hu L Y 2008 Chin.Phys.B 17 1640
[10]Yuan H C,Xu X X 2010 Acta Phys.Sin.61 064205(in Chinese)[袁洪春,徐学翔2012物理学报61 064205]
[11]Fan H Y 2008 Ann.Phys.323 1502
[12]Jiang N Q,Fan H Y,Hu L Y 2011 J.Phys.A:Math.Theor.44 195302
[13]Xu X X,Yuan H C,Hu L Y 2010 Acta Phys.Sin.59 4661(in Chinese)[徐学翔,袁洪春,胡利云2010物理学报59 4661]
[14]Dirac P A M 1966 Lectures on Quantum Field Theory(New York:Academic)
[15]Fan H Y 1993 Phys.Rev.A 47 4521
猜你喜欢
组合数与组合数公式新高考·高二数学(2022年3期)2022-04-29 排列数与排列数公式新高考·高二数学(2022年3期)2022-04-29 碘-125粒子调控微小RNA-193b-5p抑制胃癌的增殖和侵袭昆明医科大学学报(2022年1期)2022-02-28 等差数列前2n-1及2n项和公式与应用中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 基于膜计算粒子群优化的FastSLAM算法改进新疆大学学报(自然科学版)(中英文)(2020年2期)2020-07-25 数学王子高斯小天使·二年级语数英综合(2019年4期)2019-10-06 天才数学家——高斯小学生学习指导(低年级)(2019年6期)2019-07-22 Conduit necrosis following esophagectomy:An up-to-date literature review 例说:二倍角公式的巧用中学生数理化·高一版(2018年6期)2018-07-09 基于粒子群优化极点配置的空燃比输出反馈控制浙江工业大学学报(2017年5期)2018-01-22
文献[8]曾导出任意一个算符的Weyl编序形式的公式
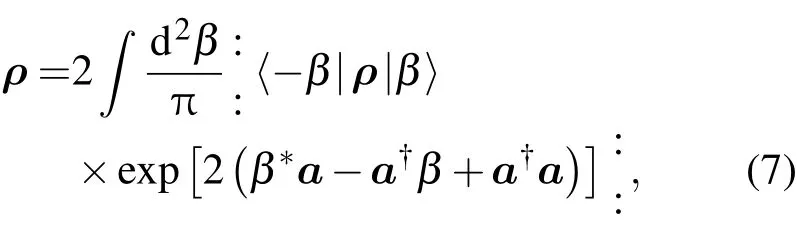

可见(7)式是正确的.由

并且利用双变量厄米特多项式的积分与表示

这里
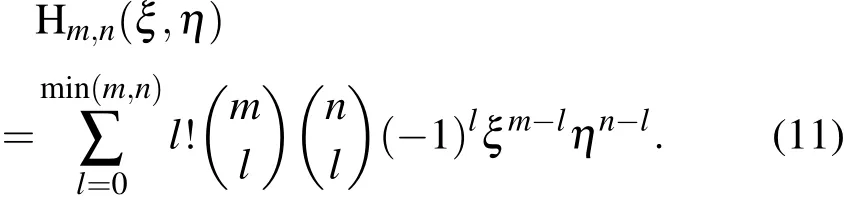
我们就可用有序算符内的积分技术[9-12]来推导出|m〉〈n|的 Weyl编序式
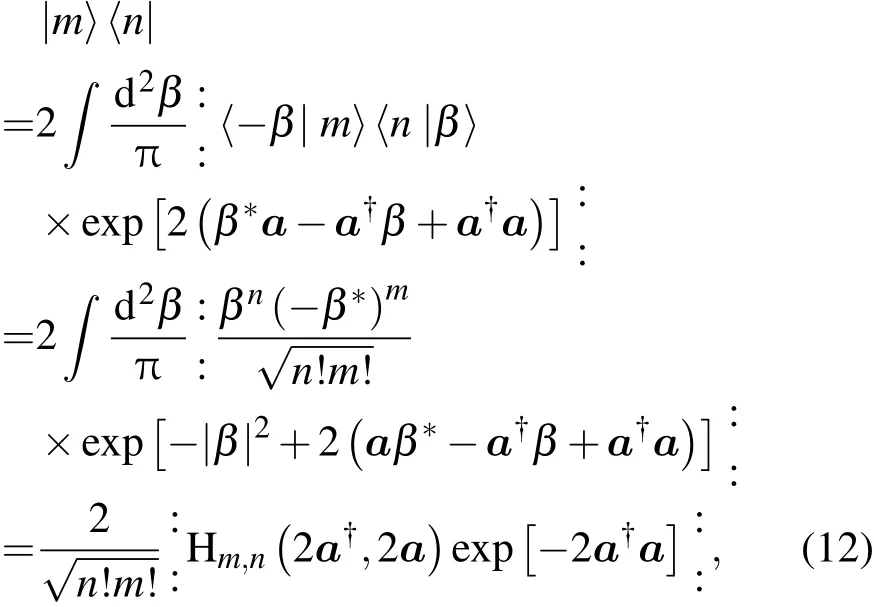
将上式代入(7)式,即可得到任一算符用双变量的厄米特多项式展开的新形式

3 光场位相算符的经典对应
作为(13)式的应用,我们来推导位相算符的Weyl编序.利用

将其代入(13)式,得到

根据Weyl量子化理论[7],位相算符 e-iφ的Weyl对应式为

由于Wigner算符Δ(α)的Weyl编序为[13]

所以对照(15)式可见

这说明位相算符的经典对应是
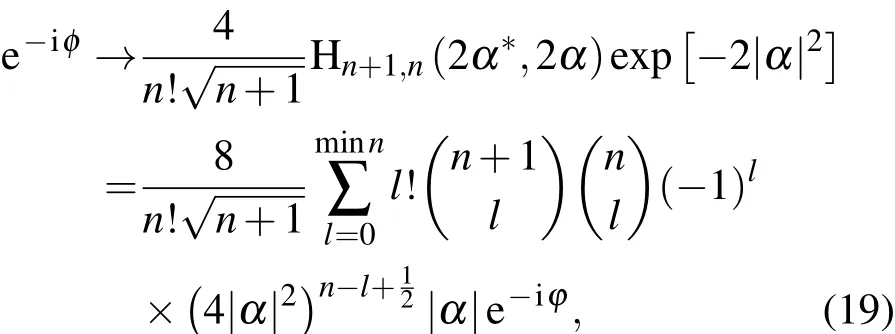
可见位相算符 e-iφ对应的经典位相体现在 eiφ,
同样我们也可以算出 eiφ的Weyl编序式
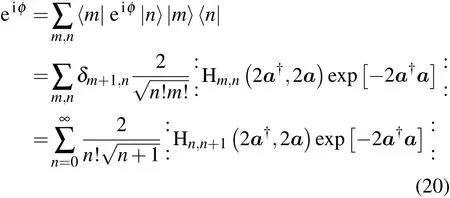
所以算符 eiφ的经典对应为
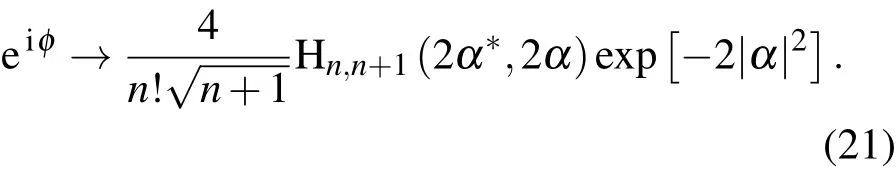
4 产生算符和湮灭算符的逆的Weyl编序式及应用
Dirac[14]首先考虑了湮灭算符的逆a-1.既然产生算符描述光子产生过程,产生算符的逆应该描写光子湮灭过程;反之,湮灭算符的逆应该描写产生过程.但要注意由于a|0〉=0,尽管aa-1=1,但a-1a/=1.用相干态和围道积分的方法[15]可以将粒子数态|n〉表示为
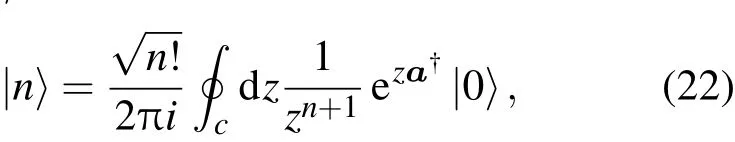
这里的围道C包括了z=0点,在围道积分下a-1e z a†|0〉=z-1ez a†|0〉就有了意义,于是有
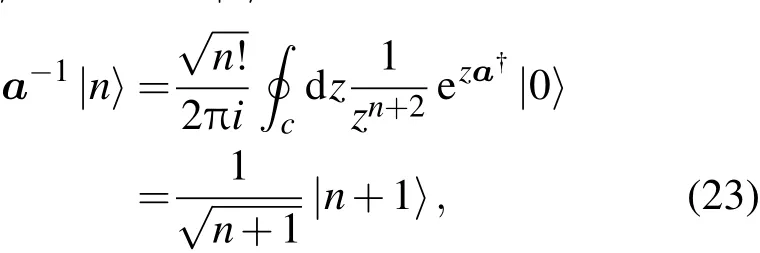
即

a-1满足

利用(24)式得到

将
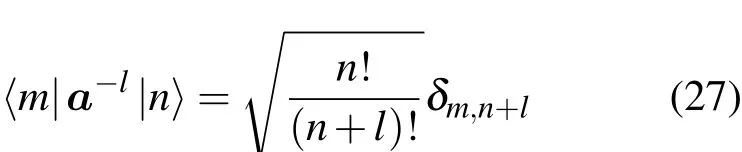
代入(13)式得到
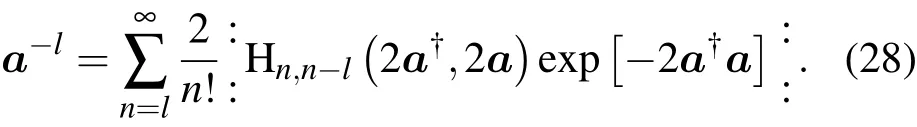
另一方面,直接利用(7)式又有

该式代入时利用了 a-1|β〉=β-1|β〉,比较 (28)和(29)两式得到

由于Weyl编序中,产生算符与湮灭算符是可交换的,可以将其看作积分参量,从(30)式得到一个新的积分公式

注意β-l是负幂次,所以这个积分带有瑕点,不易用常规的方法积分,这里用Weyl编序方法绕过了这一困难.()
同样我们可以推导出a†-l的Weyl编序
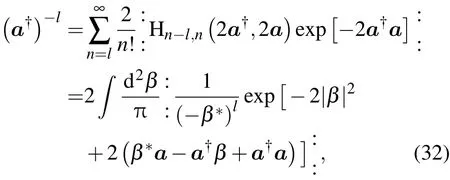
由此可以悟出带负幂次(β∗)-l的新高斯积分公式

进一步由(24)式可见

将

代入(13)式得
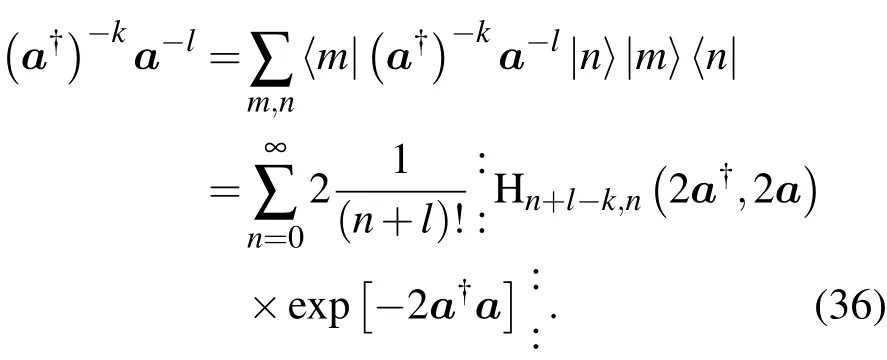
另一方面,直接利用(7)式又得到

比较以上两式,可以悟出关于带负幂次(β∗)-kβ-l的新高∫斯 积分公式

进一步可改写为
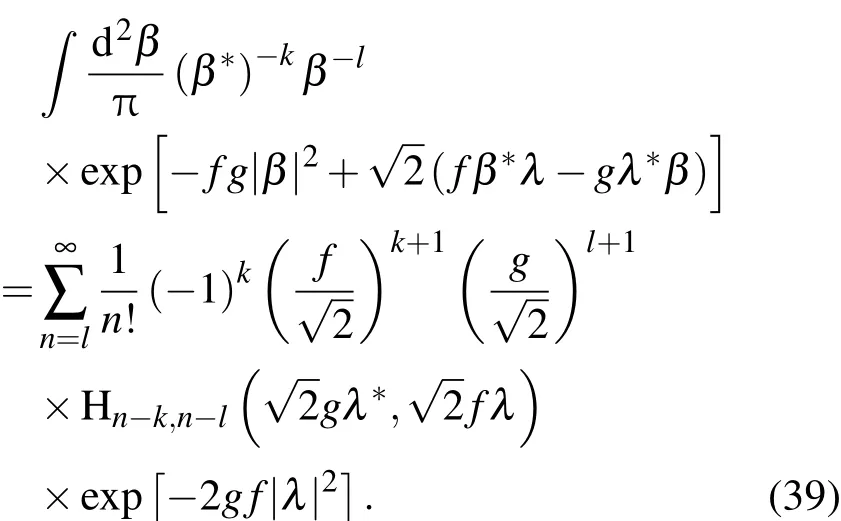
作为比较,我们推导带正幂次(β∗)kβl的新高斯积分公式.将


另一方面,将(a†)kal直接代入(7)式得
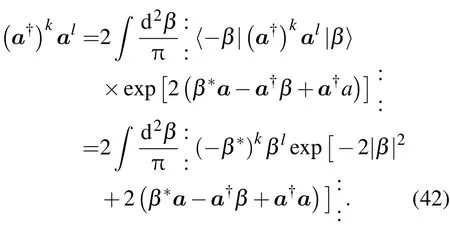
比较以上两式,可以悟出关于带正幂次(β∗)kβl的新积分公式
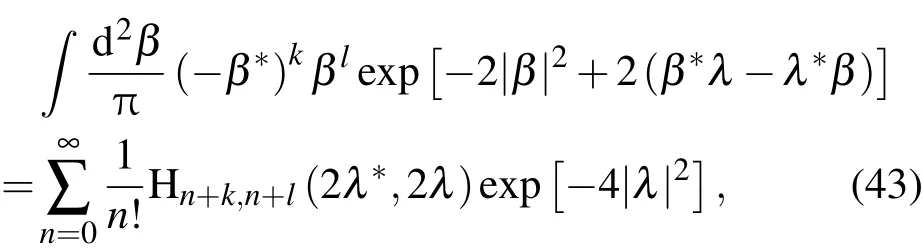
另一方面利用(10)式得到
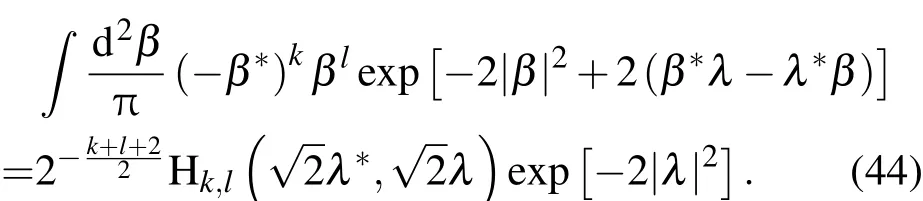
比较(44)与(45)式,得出关于双变量厄米特多项式的一个新的母函数公式
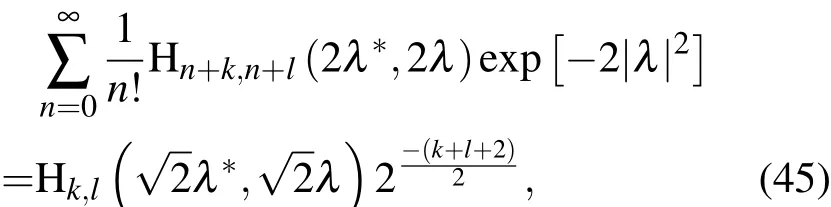
该式也可利用其他方法验证.
(45)式进一步可改写为
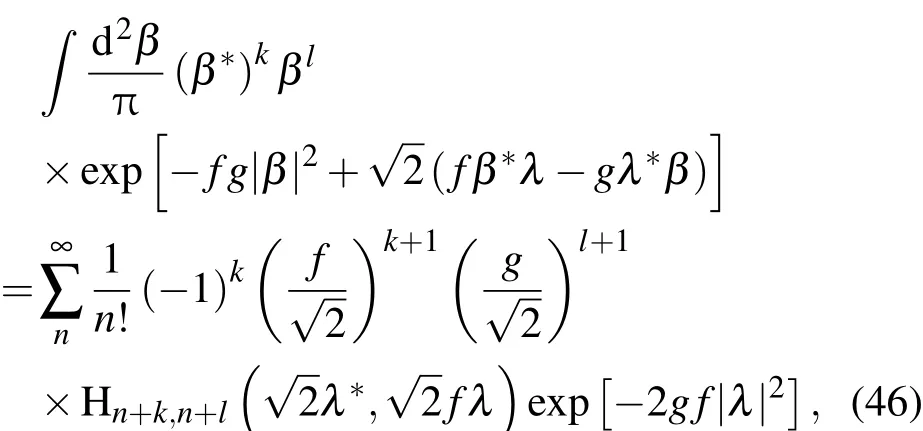
该式正好与(41)式相匹配.
5 结论
本文推导出了光场位相算符的Weyl编序,写出了其经典对应,这对于深入了解光场算符的性质提供了一种新的途径;推导了产生算符与湮灭算符的逆的Weyl编序,并据此推导出了某些特殊函数的新的生成函数和带负次幂的高斯积分公式.
[1]Dirac PA M 1927 Proc.R.Soc.London A 114 243
[2]Carruthers P,Nieto M M 1968 Rev.Mod.Phys.40 411
[3]Wigner EP1932 Phys.Rev.40 749
[4]Klauder JR,Skagerstam B S1985 Coherent States(Singerpore:World Scientifi c Publishing)
[5]Scully M O,Zubairy M S 1997 Quantum Optics(United Kingdom:Cambridge University Press)
[6]Glauber RJ1963 Phys.Rev.130 2529
[7]Weyl H 1927 Z.Phys.A 46 1
[8]Fan HY 1992 J.Phys.A 25 3443
[9]Fan H Y,Hu L Y 2008 Chin.Phys.B 17 1640
[10]Yuan H C,Xu X X 2010 Acta Phys.Sin.61 064205(in Chinese)[袁洪春,徐学翔2012物理学报61 064205]
[11]Fan H Y 2008 Ann.Phys.323 1502
[12]Jiang N Q,Fan H Y,Hu L Y 2011 J.Phys.A:Math.Theor.44 195302
[13]Xu X X,Yuan H C,Hu L Y 2010 Acta Phys.Sin.59 4661(in Chinese)[徐学翔,袁洪春,胡利云2010物理学报59 4661]
[14]Dirac P A M 1966 Lectures on Quantum Field Theory(New York:Academic)
[15]Fan H Y 1993 Phys.Rev.A 47 4521

