利用ANSYS软件分析滚动轴承接触问题

韦春翔 李伟伟 黄志平 叶 冬

(上海三一精机有限公司，上海 201200)

工程实际中广泛存在的接触问题是一种高度非线性问题，两接触体间的接触应力随着外载荷的变化而变化，接触体的变形和接触边界的摩擦作用使得部分边界条件随载荷的施加过程不同而变化。轴承作为现代机械传动部分中十分重要的一环，它依靠内部各构件间的滚动接触来支撑转动零件实现运动和力的传递，其工况的好坏直接影响整机的运行。滚动轴承的接触问题体现在两方面:(1)滚动体与内外圈间的接触应力大小;(2)轴承在载荷下的变形量。但是接触问题的求解一般是比较困难的，目前常用的是数值解法。而数值解法又分为有限元法、有限差分法、边界单元法等。其中有限元法是在工程上应用最为广泛的方法，它可以用来分析较复杂的接触问题。本文以机械中常见的滚珠轴承为分析对象，利用ANSYS软件对滚珠轴承进行分析，并将得到结果与实际变形结果对比，得出利用ANSYS分析轴承接触问题的可行方法。

1 轴承的三维接触有限元分析

1.1 轴承样例

以常见的6300为例:材料为GCr15，外径D=35 mm，内径d=10 mm，宽度B=11 mm，钢球直径Dw=6.35 mm，内圈沟道曲率半径Ri=3.27 mm，内圈沟道沟底直径Di=17.15 mm，外圈沟道曲率半径Re=3.334 mm，外圈沟道沟底直径De=29.85 mm，接触角α=0，钢球数量Z=7。

材料参数:弹性模量E=207 000 MPa，泊松比μ=0.3。径向载荷Fr=3 472 N。最大承载钢球径向载荷Q=2 480 N。

1.2 轴承的三维实体建模

角接触球轴承机构需考虑内外圈不同的曲率半径，形状比较复杂，直接利用ANSYS内部的建模功能不能精确地建立轴承的几何模型，势必造成几何形状上不必要的误差。通常在CAD软件中建立实体模型，利用CAD软件与ANSYS的接口导入ANSYS，所以先根据该型号轴承的尺寸，在Pro/E中建立几何模型(在此忽略保持架)。接着启动ANSYS，选择菜单File＞Import＞Pro/E，打开ANSYS的Pro/E的接口对话框，选择刚保存的轴承装配体文件，如图1。

1.3 单元选择及网格划分

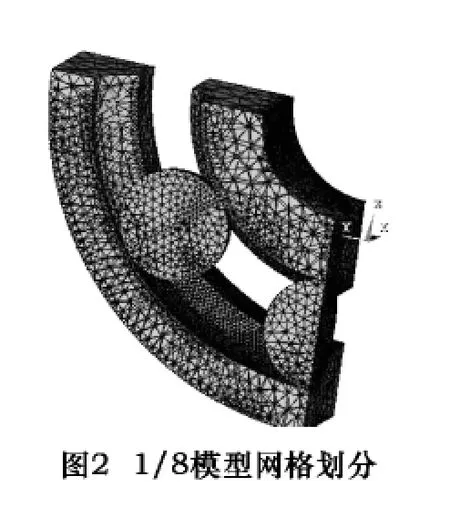
ANSYS中定义两物体接触是通过设置两接触体的接触面来实现的，为了减少后续有限元模型的单元数，以节省出更多的计算机资源来精确地求解接触问题，对轴承滚道面与滚珠面接触的范围与面积参考经典理论计算的结果，只建立1/8的模型，采用8节点离散三维实体单元Solid45，进行网格划分(Smart4级精度)。

1.4 轴承接触问题的描述

接触问题一般分为两种基本类型:刚体—柔体的接触和半柔体—柔体的接触。ANSYS10.0支持三种接触方式即:点—点、点—面和面—面，每种接触方式使用特定的接触单元。轴承问题明显属于面面接触，模型中的接触单元选用Targe170即钢球面，Contact174即圈体面。如图3所示接触对。

1.5 边界条件及加载

由于分析模型只选取1/8的圈体分析，因此剖面处应加对此约束;轴承通常安装在刚性很大的轴和轴承座上，因此约束轴承外圈的全部自由度;径向力在轴承的实际状态中通过轴传到内圈上，以集中力的形式施加在内部表面的轴向线的节点上。

1.6 有限元分析结果

(1)显示结果

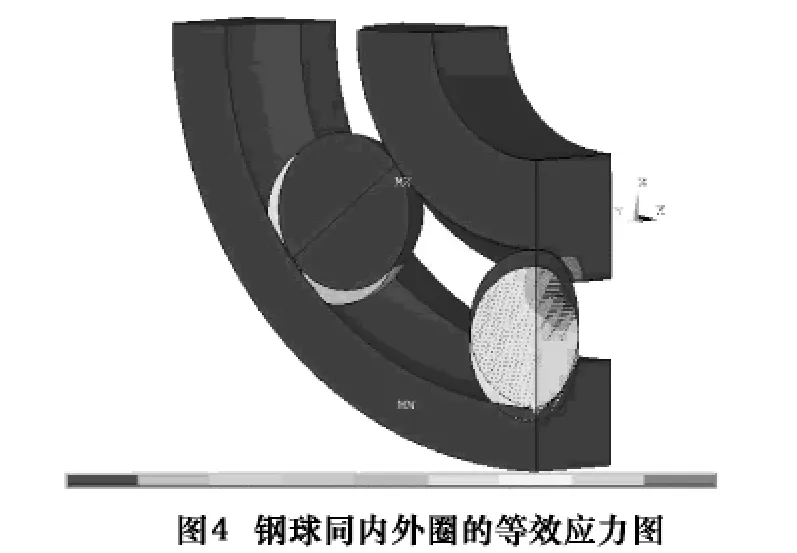
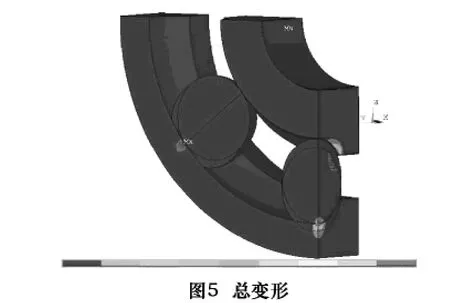
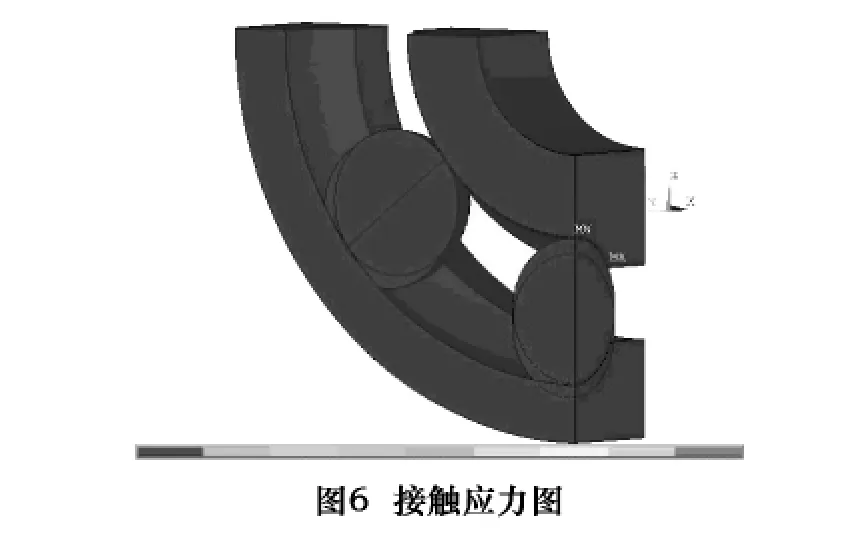
通过ANSYS后处理分析，得到最大载荷作用下钢球同内外圈的接触结果。图4、图5所示的分别是钢球同内外圈的等效应力和模型的总变形。模型的接触应力如图6所示。

(2)结果分析

从上面ANSYS进行有限元分析所得的结果可以看出，应力最大的地方发生在钢球与内圈接触处，这与理论计算中预期的初始接触点一致。从图4可以很清楚地看出，两个相同材料接触体内部的接触应力是不同的，外圈最大接触应力在与钢球接触的位置，最大应力为3 350.8 MPa。而内圈最大应力发生在内圈滚道边缘，最大应力P=3 882.6 MPa。

从图5得知，内圈的接触变形为长轴a=1.854 mm，短轴b=0.158 mm;外圈的接触变形为a=1.452 mm，b=0.254 mm。

2 滚动轴承实际工况

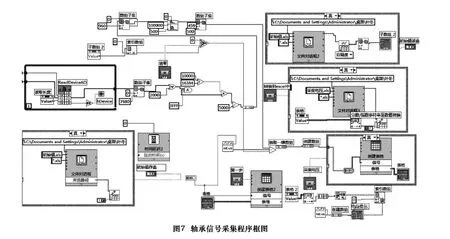
为了验证 ANSYS分析结果的准确性，本文对6300轴承在载荷下的真实工况进行了监测。采用Labview8.2编写信号采集软件，在轴承受力部分贴应变片，采集其受力变形的电信号。硬件部分采用了Usb2080的14位信号采集卡、信号放大器、巴特沃斯滤波器等等。其程序框图和显示框图如图7和图8。

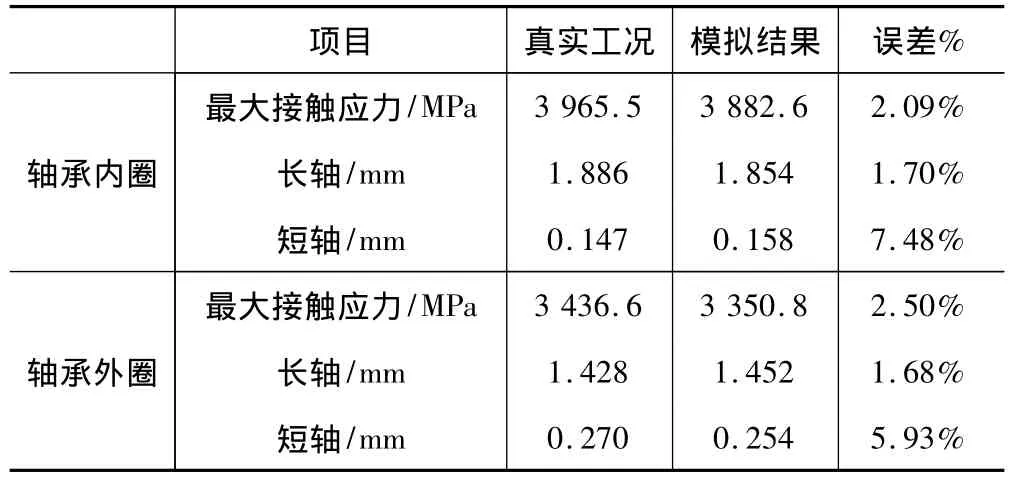
表1 模拟结果精度分析

轴承在真实工况下的变形结果与ANSYS模拟结果对比见表1。

3 结语

(1)比较有限元分析结果与实际工况，轴承内圈的最大应力与实际结果误差为2.09%，外圈误差为2.50%，表明该模型有限元模拟的准确性。

(2)用有限元法对轴承进行数值模拟，得出的接触应力都比等效应力大，表明轴承的失效主要是由接触应力过大造成的，这与实际工程中滚动轴承失效情况一致。

［1］濮良贵，纪名刚.机械设计［M］.8 版.北京:高等教育出版社，2006.

［2］Harris T A.Rolling bearing analysis［M］.California:John Wiley and Sons，1991.

［3］王大力，孙丽明，单服兵，等.ANSYS在求解轴承接触问题中的应用［J］.轴承，2002(9):1 －4.

［4］王建伟，罗宁.有限元法在分析轴承接触问题中的应用［J］.轴承，2004(12):1－3.

［5］伍生，曹保民，杨默然，等.滚动轴承接触问题的有限元分析［J］.轴承，2007(6):70 －72.

［6］郑志坚，潘玲.基于ANSYS的推力滚子轴承接触分析［J］.福州大学学报，2009(4):224－227.

［7］陈锡辉，张银鸿.Labview8.20程序设计从入门到精通［M］.北京:清华大学出版社，2012:1－90.