滚珠丝杠进给传动系统控制器参数优化*

杨 涛 张为民② 张月磊 杨 勇

(①同济大学机械与能源工程学院，上海 201804;②同济大学中德学院，上海 200092)

随着现代科学技术的进步，高速精密数控加工成为现代制造业发展的必然趋势，而数控机床的工作性能很大程度上取决于伺服进给系统的动态性能。故如何通过机械结构改良和控制系统优化来提高机床进给传动系统动态特性已成为国内外研究的热点问题。围绕数控机床进给传动系统的动态特性，国内外学者已做了大量研究工作，其中通过改良机械传动系统的结构特性［1－3］和利用计算机建模仿真［4－5］的方法都已发展较为成熟，但对于通过各环节控制器参数优化来提高进给传动系统动态特性方面却少有学者涉足。

伺服系统中各环节控制器的参数设置对伺服系统控制系统有着重要的意义。控制器参数的改变会引起伺服系统特性的变化，从而影响机床的动态特性和加工特性。因此，本文以采用间接测量的数控机床滚珠丝杠进给传动系统为研究对象，建立伺服系统控制回路和机械环节的数学模型，利用复比法对各环节控制器进行参数优化，并结合实例分析滚珠丝杠进给传动系统伺服控制器的优化设计效果。

1 优化目标

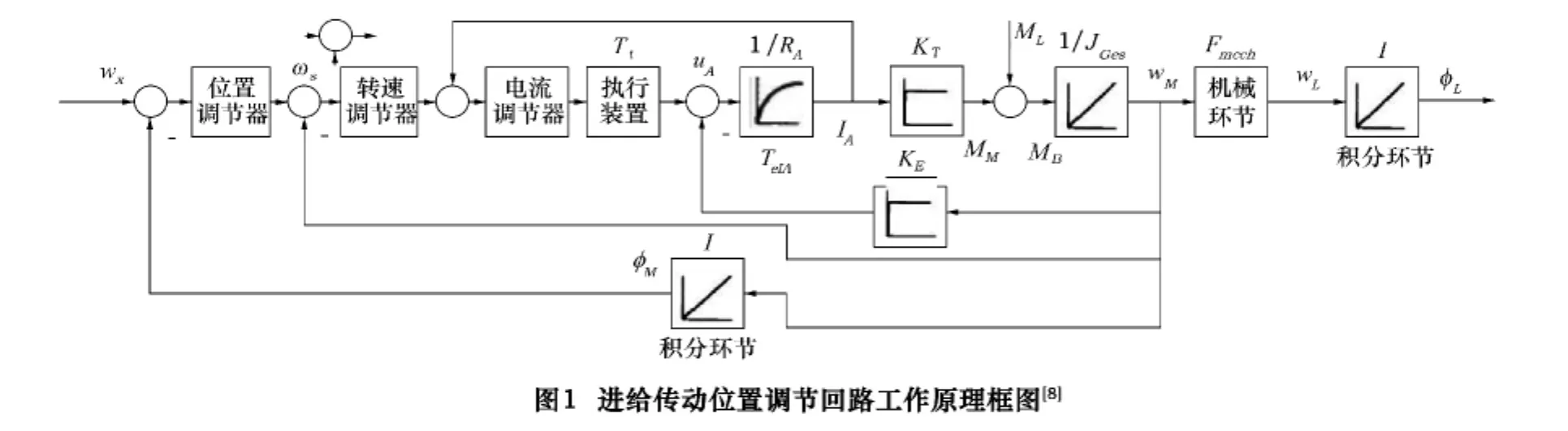
在数控机床中，对位置调节回路的要求是:其所属进给单元根据所存储的几何数据和速度数据尽可能无延时，且无畸变地跟踪数控装置中所形成的位置基准量。如图1所示，间接测量的进给传动位置调节回路可抽象为伺服系统控制模块和机械传动模块的串联，其中控制模块包括位置环、速度环和电流环。因此本文对机床进给传动系统进行控制器优化的目标是使伺服控制系统与机械传动环节的动态特性相匹配，实现“机电耦合”的优良动态响应特性。

2 优化原理

2.1 调节技术

进给传动系统采用级联调节，从最内环到最外环依次用于调节电流、电动机角速度和电动机角位置，并且上级主调节器的输出量等于下级局部调节回路的基准量。通常情况下，调节回路主要由调节装置、调节对象和测量装置组成。其中，输出量x与基准量w的关系就是相应传递环节的传递特性。

2.2 复比法

复比法是一种以闭环调节回路的阻尼最优法为准则的方法［8］，其推导目标是:闭环调节回路的频率响应特性在更大的频率范围内具有0 dB(或1)这个值。闭环调节回路的频率响应特性方程的一般形式为

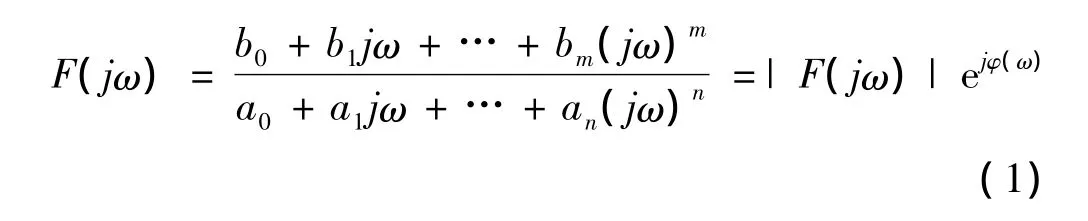
当分母的最后一项向前构成系数之比，且相邻两个比值又构成如下关系

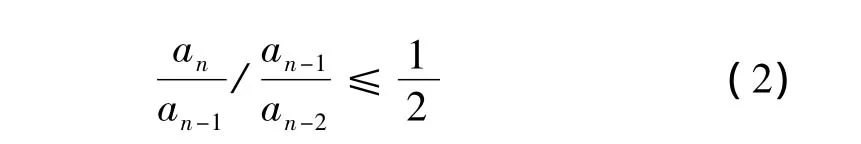
就可以获得响应速度快，超调量小的最优阻尼频响特性。以此类推，就可以确定从a0到an的所有参数的值，并且整定的参数对调节对象中的参数变化和所进行的近似计算具有不敏感的鲁棒特性［6］。

3 调节器的优化

3.1 电流调节器参数整定

如图1可知，电流环中的调节对象由延迟时间为TeIA，比例系数为1/RA的P－T1环节和具有纯时滞的Tt的晶体管斩波器组成，将纯时滞和滤波器延迟组合成小延迟时间总和TσI，则此调节对象的频率响应函数为

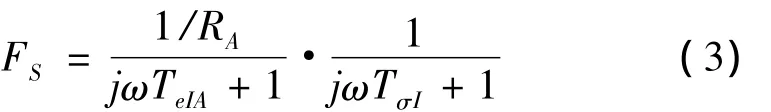
为了补偿调节对象中的大延迟时间，提高电流环调节速度，电流环采用常规PI调节器，其频响函数为

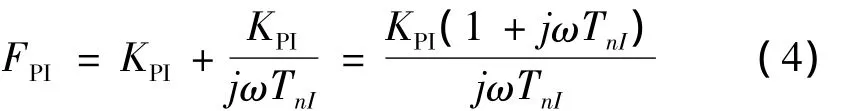
设置调节器的超前时间TnI=TeIA，则将对电流环调节对象中的大延迟时间进行补偿，使之为零。经约分后的电流环的闭环频响函数为

利用复比法，由式(2)可得

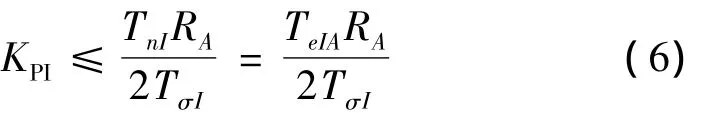
将式(6)代入式(5)，并忽略具有(jω)2的因式项，则可将电流调节回路的二阶频率响应特性近似地描述为P－T1环节，即

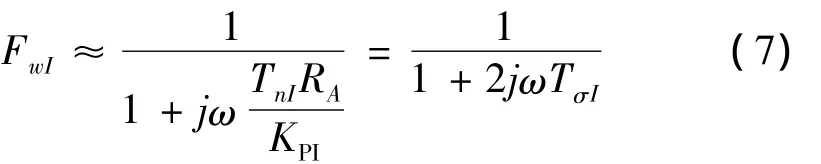
且电流环的等效延迟时间TEI=2TσI。

3.2 转速调节器参数整定

电流调节回路用延迟时间为TEI的P－T1环节代替，并与延迟时间2TATn组合成转速调节回路的小延迟时间总和Tσn，则

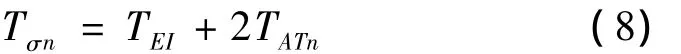
同时将转矩常数KT计入转速调节器的比例系数KPn中来简化模型。当采用常规PI调节器时，可得等效延迟时间为TEn=4Tσn的P－T1环节。

如果采用参考PI调节器，由于转速调节回路的基准频率响应特性中参考PI调节器只起到比例系数为KPn的P调节器作用［8］，则转速调节回路的基准响应特性为

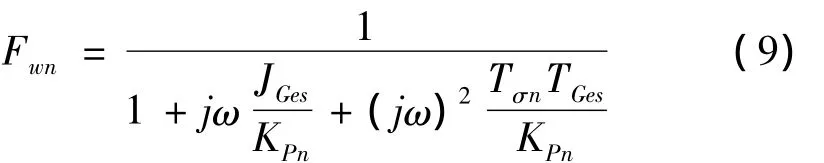
根据复比法，由公式(2)可整定出

将式(10)代入式(9)，并忽略具有(jω)2的因式项，则可将转速调节回路的二阶频率响应特性近似地描述为P－T1环节，即

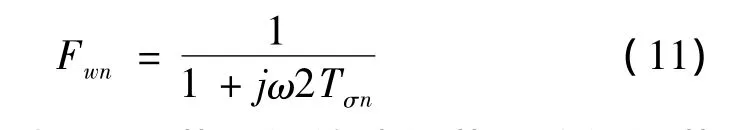
可见采用参考PI调节器的转速调节回路的调节时间为采用常规PI调节器的一半，因此对于转速调节回路，选用参考PI调节器，且转速调节回路的等效延迟时间TEn=2Tσn。

3.3 位置调节器参数整定

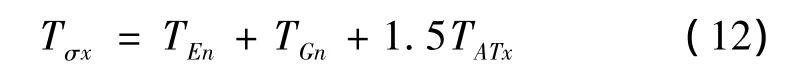
位置调节回路采用比例系数为KV的P调节器，且位置调节回路的小延迟时间为式中:TEn为转速调节回路等效延迟时间，TGn为转速给定值延迟时间，并考虑用0.5TATx作为采样－保持环节和TATx作为调节算法的运算周期。因此，位置调节回路的闭环基准响应特性为

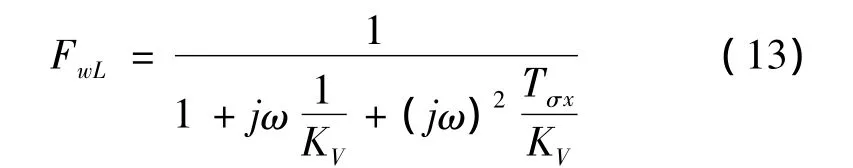
根据复比法，亦可整定出

考察机械传动环节对KV参数整定的限制作用时，由于转速调节回路的特征角频率ωnA通常远远高于机械传动环节的最低固有角频率ωdmin，ωnA时的激增值在机械固有频率范围对位置调节回路合成幅值响应特性方面不产生影响，故只考虑TGn作为位置调节回路的小延迟时间，则式(13)可简化为

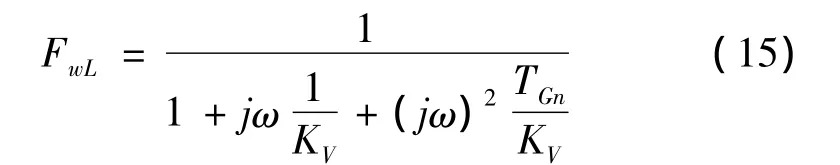
可计算出最低机械固有角频率时的幅值响应特性的绝对值

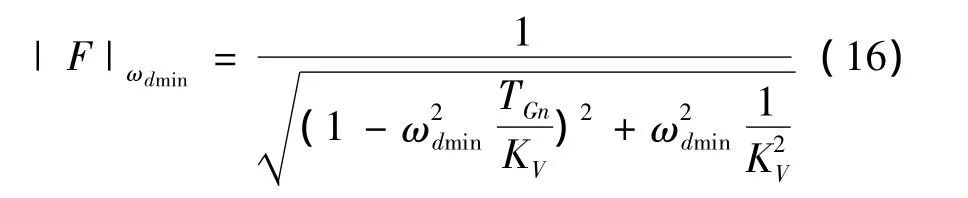
如果想达到在最低机械固有频率时具有激增值H的位置点上，得出包括机构在内的位置调节回路的幅值响应特性为≤0 dB(或者≤1)这一目的，就必须将这个绝对值乘以激增值H，从而可以得到下列方程

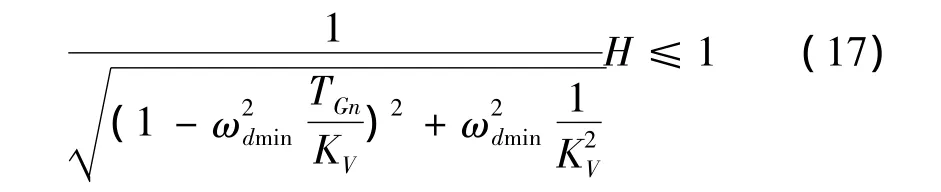
此处同时考虑公式(14)的影响，则可以整理出KV系数的解为

4 实例

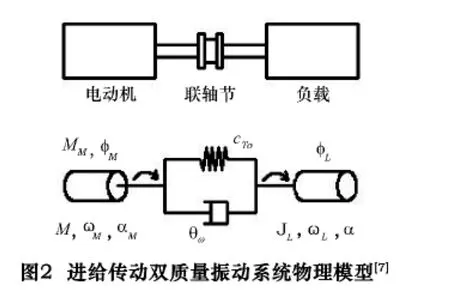
本文以一款采用滚珠丝杠进给传动系统的卧式加工中心为例，分析该控制器优化设计方法对机床进给传动系统伺服控制器的优化效果。为了简化模型，这里引用Zirn提出的由电动机和耦合连接负载组成的双质量振动系统的简化方案［7］，如图2所示，其物理关系为

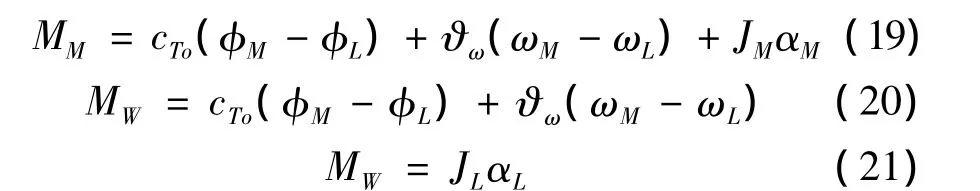
式中:MM和MW分别为电动机转矩和轴转矩;JM和JL为电动机和负载的转动惯量;φM和φL分别为电动机和负载转角;ωM和ωL分别为电动机和负载的角速度;αM和αL分别为电动机和负载的角加速度;cT0为扭转弹簧系数;ϑω为阻尼系数。

联立上述方程组，并通过拉普拉斯变换可得此双质量振动器系统的频率响应特性为

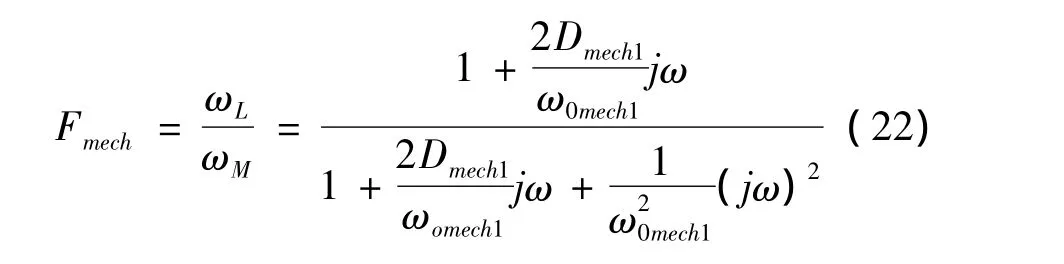
其中特征角频率和阻尼系数分别为

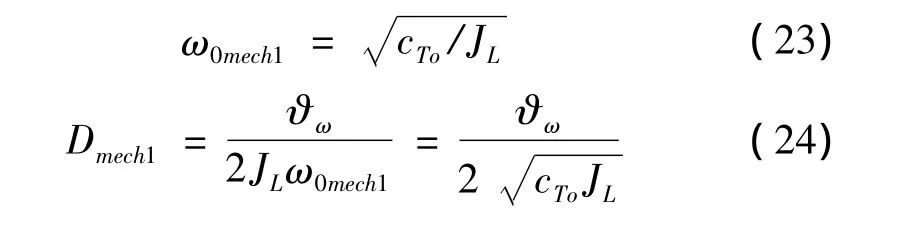
通过对滚珠丝杠进给传动机构进行激振力模态测试，可近似得到双质量振动器的固有角频率ωdmin=130.6 s－1(或fdmin=20.8 Hz)和相应的阻尼系数Dmech=0.023。而双质量振动器的零点频率ω0mech1和Dmech1的值可由下面的关系得到

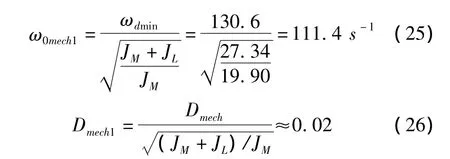
联立式(22)、(25)和(26)，可计算机械系统传递函数ωL/ωM下的最大振幅H=16.8，即24.5 dB。

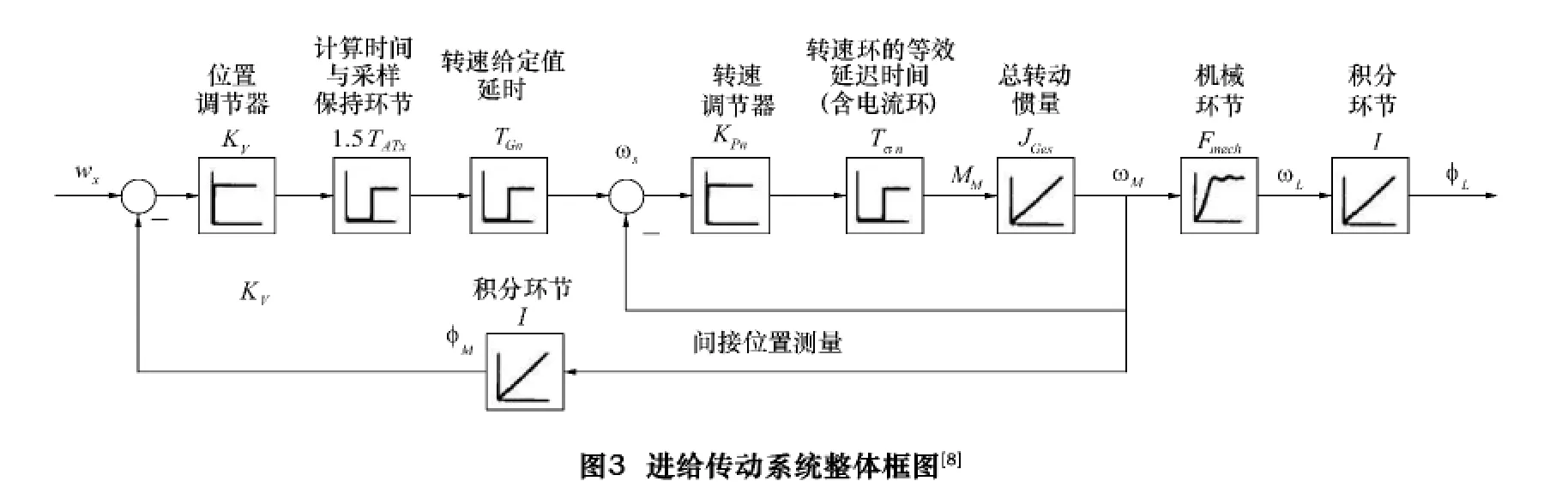
现在可建立进给传动系统的整体框图如图3所示，其中整定的初始条件为TATx=2 ms，TATx=100 μs，TEI=150 μs，JM=19.90 × 10－4kg·m2，JL=7.47 ×10－4kg·m2，ω0mech1=111.4 s－1，Dmech1=0.02。

由式(8)和(10)分别可得Tσn=0.35 ms，KPn≈3.91 N·m·s/rad，将 ω0mech1和Dmech1的值代入式(22)可得

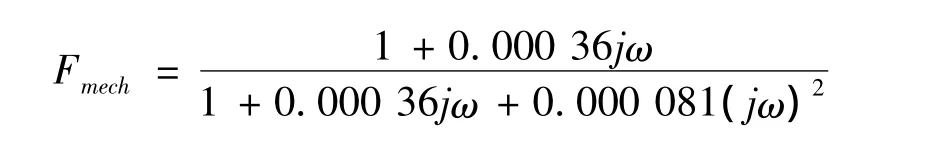
因此，只需要一个参数就能确定KV，但其设定过程复杂且需要一系列迭代计算:

(1)如果假定转速给定值延迟时间TGn=15 ms，则由式(12)可得Tσx=18.45 ms，并通过式(14)可得出最大的KV系数为KVmax=27.1 s－1。

将TGn/Tσx=0.81和绝对值H=16.8代入式(18)得KVmax/ωdmin=0.157，则KVmax=17.49 s－1＜ 27.1 s－1，因此，转速给定值延迟时间可以给得大一些。

(2)如果假定一个TGn=30 ms的延迟时间，那么可得Tσx=33.45 ms，相应地可得到KVmax=14.95 s－1。

将TGn/Tσx=0.819 7和绝对值H=16.8代入式(18)得KVmax/ωdmin=0.164，则KVmax=18.27 s－1＜14.95 s－1，因此，转速给定值延时必须给得小一些。经过数次迭代，最终确定TGn=24 ms，TGn/Tσx=0.874，KV=18.1 s－1。

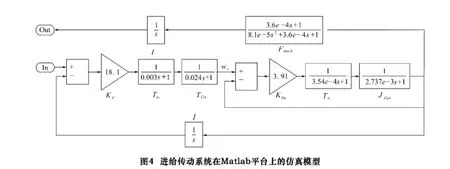
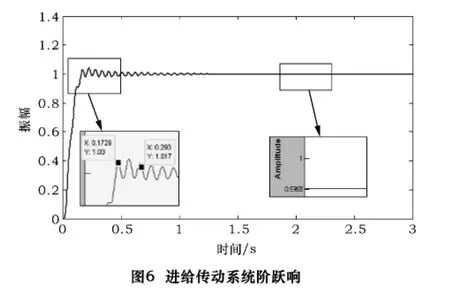
至此，所有参数都已确定，可在Matlab平台上建立进给传动系统仿真模型(如图4)。分析可得整个进给传动系统的频率响应特性伯德图如图5所示，系统的阶跃响应如图6所示。

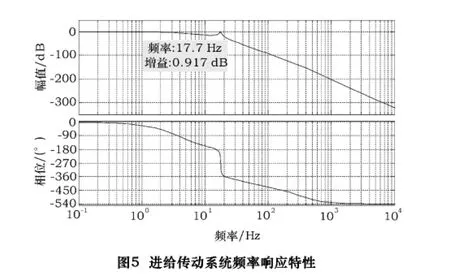
由图5可知，控制回路的设计满足进给传动系统的性能要求，且其良好的阻尼特性能够获得很小的超调量，确保了系统的稳定，并且当频率在一个大范围内变化时它的幅值都保持在0 dB。由图6可知，进给传动系统的调节时间为0.293 s，超调量只有3%，并且稳态误差控制在0.02%以内。

5 结语

本文提出了间接测量的进给传动系统伺服控制器的参数优化技术，涉及到控制器的选择方案及其内部参数的优化方法，并通过实例中的滚珠丝杠进给传动系统验证了控制器参数优化的合理性。根据本文提出的控制器参数优化技术，可以获得一个稳定的进给传动系统，该系统调节时间小于0.3s，超调量为3%，且稳态误差小于0.02%。

［1］Hjink J A W.Analysis of a milling machine:Computed results versus experiment date［J］.M.TD.R，1973(14):26 －30.

［2］Yoshimura M.Computer aided design improvement of machine tool structural incorporation joint dynamic［J］.Annals of CIRR，1979(28):241－246.

［3］唐文成，易红，唐寅.机床大件结构的拓扑优化设计［J］.东南大学学报，1996，26(5):22 －26.

［4］王德斌.交流伺服进给系统及其数学模型的研究［J］.机械制造与自动化，2006，35(1):86 －88.

［5］董玉红，张立勋.数控机床进给伺服系统的检测方案及仿真研究［J］.自动化技术与应用，2004(2).

［6］Naslin P.Dynamik linearer and nichtlinearer systeme:Muechen［M］.Oldenburg Verlag，1968.

［7］Zirn O.Beitrag zum entwurf von vorschubantrieben fuer die hochgeschwindigkeitsbearbeitung［D］. Diss. EidgenoessischeTechnische Hochschule Zuerich，1996.

［8］(德)Grob J H，Hamann G，Wiegartner.自动化技术中的进给电气传动(基础计算设计)［M］.熊其求，译.北京:机械工业出版社，2002.