精密复合数控磨床伺服进给系统优化设计

丁庆新 李 岩 赵宏林 田 非

(中国石油大学(北京)，北京 102249)

精密复合数控磨床是保证航空业、军事及光学元件等尖端领域发展的关键设备［1］。国家在高档数控机床与基础制造装备科技重大专项(2009ZX04001－122)子课题精密复合数控磨床的研制中提出了要达到国际同类产品的技术水平。磨床采用直线电动机伺服系统，其加工精度主要取决于系统的动态特性［2－3］。对磨床伺服系统进行建模和优化，可以得到系统动态特性的最优匹配参数，从而对数控机床参数调节具有指导意义。

1 直线电动机伺服系统建模

1.1 直线电动机数学模型

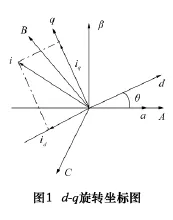
在永磁同步电动机中，建立固定于转子的参考坐标系。d－q为转子两相坐标系，A－B－C为定子三相坐标系，α－β为定子两相坐标系。d轴与参考轴之间的角度为θ，d－q旋转坐标图如图1所示。设电枢在d－q坐标系中的直、交轴电流分别为id、iq，以运动部分的速度v和位移x作为状态变量，可以推导出直线电动机电流、速度、位移的状态方程如下所示:

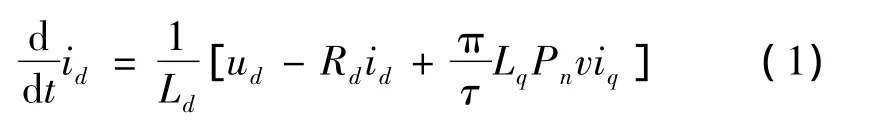
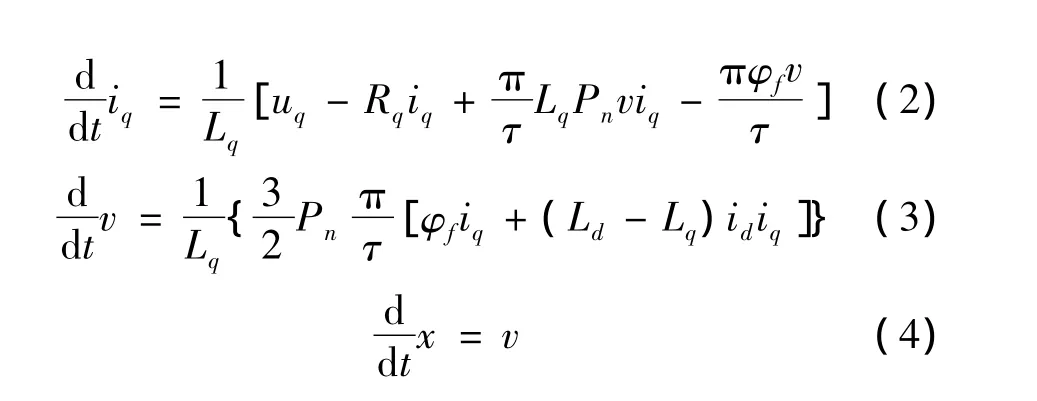
式中:ud、uq为动子电压;id、iq为动子电流;φa、φb为三相定子绕组的磁链;Rd、Rq为相绕组电阻;Ld、Lq为动子电感;φf为永磁体产生的磁势;Pn为极对数。根据dq坐标系下的数学模型建立线性状态方程如下:

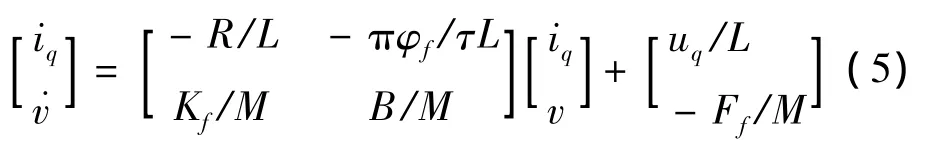
式中:M为直线电动机动子质量;B为粘滞摩擦系数;Ff为负载阻力;L=Ld=Lq;Kf为推力系数。

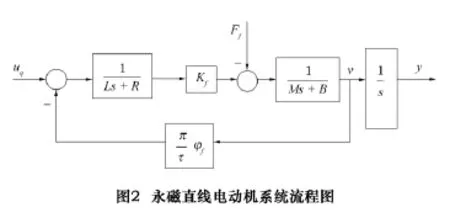
在零初始状态下，对状态方程求拉氏变换，令uq为输入，速度v为输出，得到永磁直线电动机系统流程如图2所示。

1.2 伺服系统结构

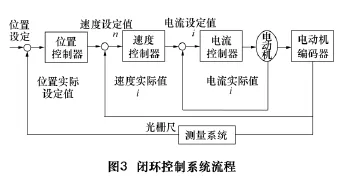
本文研究对象为西门子SIMODRIVE611D驱动控制器，该驱动控制器主要包括电流环、速度环和位置环3个部分。整个控制流程是先通过位置环控制器，到速度环控制器再到电流环控制器，最终控制电动机，同时电动机将信号反馈到电流控制器和速度控制器，编码器将位置信号反馈给位置环控制器［2－3］;前一级优化对后一级产生影响，电流环影响速度环，速度环影响位置环，通过算法实现闭环控制的“稳、准、快”，其闭环控制系统流程图如图3所示。

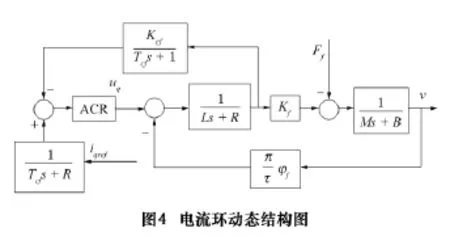
这里将对电流环、速度环和位置环分别进行讨论。直线电动机初级可以看成是由电阻和电感组成的一阶惯性环节。电流环是一个电流随动系统，电流控制器选在PI调节器，使得电流环任意情况下快速跟踪电流给定值，可以得到电流环动态结构图如图4所示。

考虑伺服系统的固有属性，可以将电流环的传递函数看成为一个小惯性环节，将其按照小惯性环节的方式处理，得到电流环闭环传递函数GiB(s)为

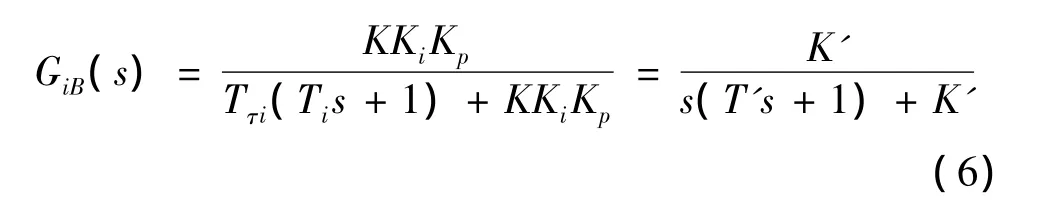
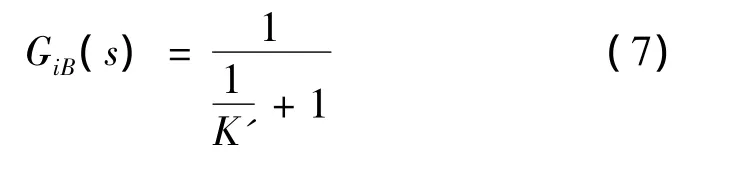
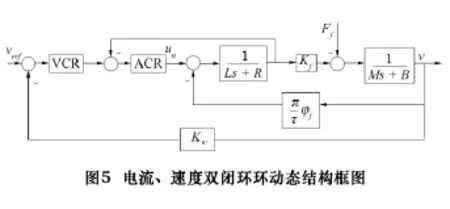
速度环在整个伺服系统中同样占有重要的地位，其性能的好坏直接影响到控制精度及响应特性。SINUMERIK 611D中的速度环一般只设置比例增益与积分时间常数两个参数，采用PI控制，添加微分环节后影响系统的响应速度。如图5所示，电流、速度双闭环动态结构框图，图中Kw为速度反馈系数。

由方框图可以得到速度环的开环传递函数为:

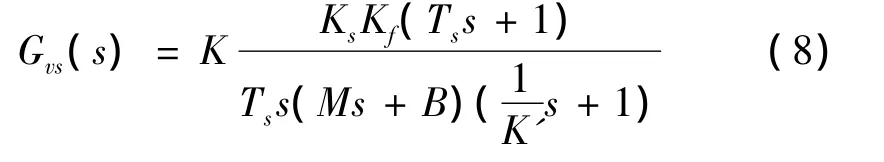
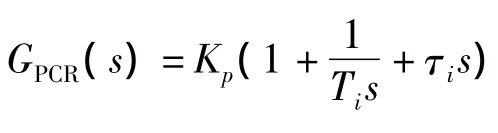
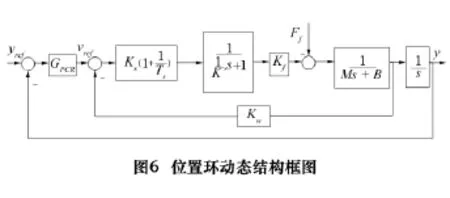
1.3 伺服系统的数学模型

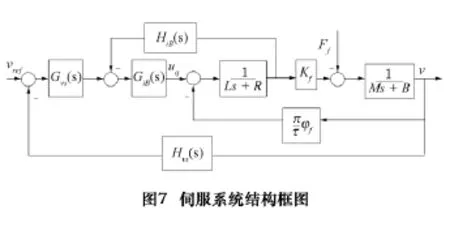
根据驱动系统模型和直线电动机模型建立的伺服系统结构框图如图7所示，式中GiB(s)为电流控制传递函数，HiB(s)为电流检测传递函数，Gvs(s)为速度控制传递函数，Hvs(s)为速度检测传递函数。

2 伺服系统优化设计

2.1 粒子群优化算法

伺服系统建模得到的目标函数比较复杂，应用解析法不太适用于参数优化设计。这里采用了粒子群优化(PSO)算法，它是一类随机全局优化技术。PSO算法可以通过粒子间的相互作用发现复杂空间中的最优区域，这种算法简单可行，对目标函数的要求不高，方法灵活，搜索过程简单，非常适合伺服系统优化。基本的粒子群算法，可以用式(9)表示，其中学习因子c1、c2的取值范围为［0，+∞］，r1、r2为随机数，其取值范围为［0，1］。

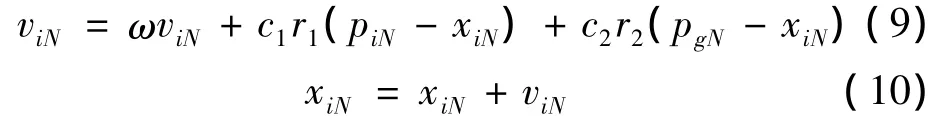
式中:viN为第i个粒子在N维空间中的速度;ω为惯性权重因子;piN为第i个粒子在N维空间经历过的最好位置;pgN为整个群体所有粒子经历过的最好位置;N为整个群体所有粒子总和。

2.2 粒子群优化算法的改进

粒子群优化算法有时会出现局部徘徊，使得目标函数优化因无法获得全局极值而收敛速度减慢甚至无法计算［5－7］，因此需要对粒子群优化算法进行改进，增加其收敛速度，加快运算速率、提高效率，下面主要对惯性权重因子ω参数进行改进。

在基本粒子群优化算法中，由于惯性权重因子的值固定不变，使得收敛速度变慢的概率增大。通过大量实验发现，应用线性递减惯性权重因子策略相对于固定惯性权重因子策略有更好的寻优效果。式(11)为线性递减惯性权重因子策略公式。

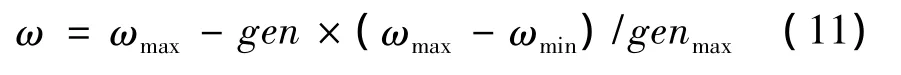
式中:genmax为最大进化代数;ωmax为最大惯性权重因子;ωmin为最小惯性权重因子。

分别使用固定惯性权重因子策略和线性递减惯性权重因子策略对一阶纯滞后系统做测试，其中通过调节时间ts，峰值时间tp，超调量σ三个指标确定两种策略的优化性能，图8为惯性权重系数ω对比仿真实验结果。被控对象传递函数为

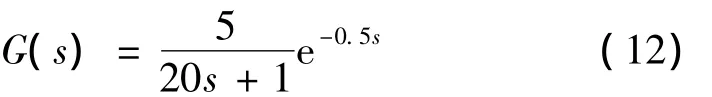
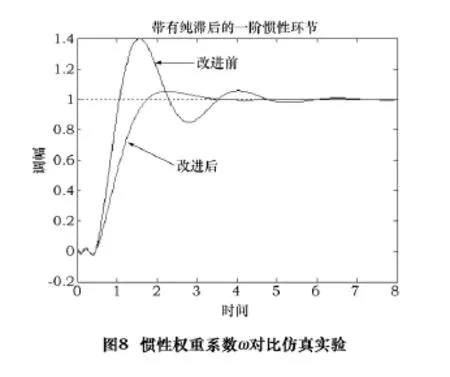
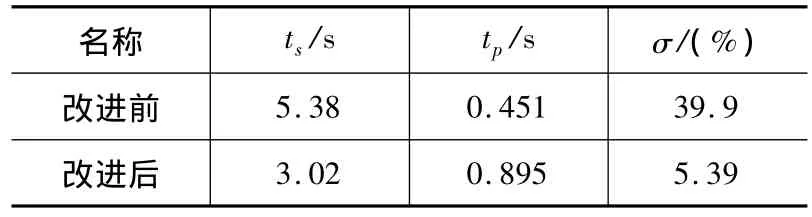
表1 惯性权重系数ω对比仿真实验结果

通过对比分析可以发现，改进后比改进前调节时间减少了43.87%，峰值时间增加了98%，超调量减少了86.49%，由此可见，改进后的线性递减惯性权重因子策略的优化性能明显强于改进前的固定惯性权重因子策略。

2.3 适应度函数

适应度函数的正确选择直接影响到寻优策略的收敛速度与寻优效率。通常使用的适应度函数有4个，分别是:偏差平方积分(ISE)、偏差绝对值积分(IAE)、偏差绝对值乘时间积分(ITAE)和偏差平方乘时间积分(ITSE)。为使系统优化策略有更大的适应范围，分别以一阶纯滞后惯性环节和二阶纯滞后惯性环节对4种适应度函数做对比仿真实验。式(13)为一阶纯滞后惯性环节传递函数，式(14)为二阶纯滞后惯性环节传递函数。

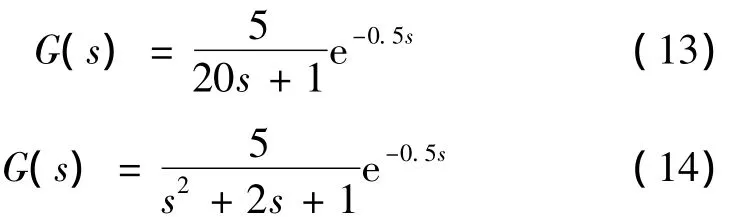
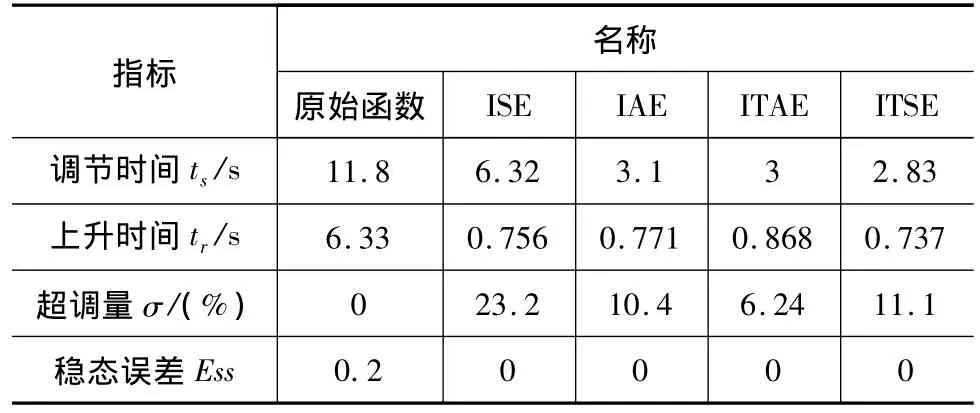
表2 一阶纯滞后惯性环节实验仿真结果

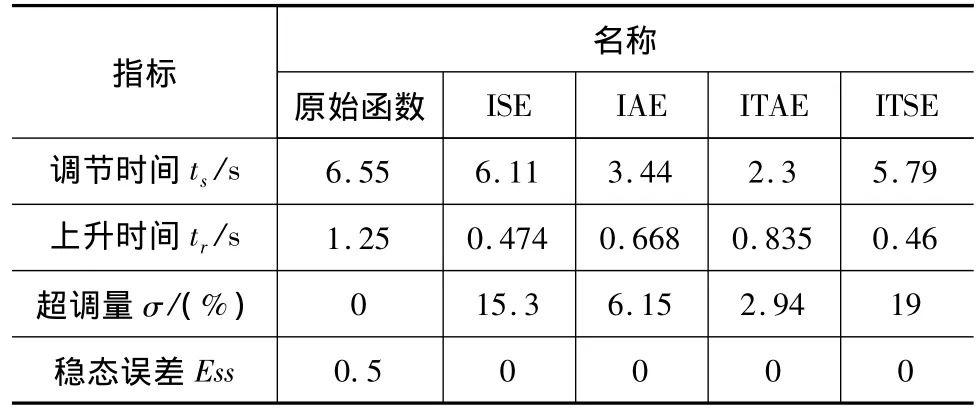
表3 二阶纯滞后环节实验仿真结果

从表2一阶纯滞后惯性环节实验仿真结果和表3二阶纯滞后环节实验仿真结果可以看出，ITAE相对于ISE、IAE和ITSE具有响应速度快，超调量小等优点，为获得更好的优化效率，优化策略中适应度函数采用ITAE。

3 实验测试

3.1 优化软件测试

根据实际机床工况，可以得到机床原始参数设定值如表4所示，多组仿真结果和实际机床参数对比如表5所示，初始条件下系统动态性能指标调节时间为0.221 s，超调量为18.97%，性能指标为0.012 4，与系统优化后(实验4结果)的动态性能指标做对比，可以得出系统优化后比优化前调节时间减少了21.4%，超调量增加了5.3%，峰值时间减小了16.7%，综合性能提高了26.53%，验证该算法优化效率高，可靠性强。

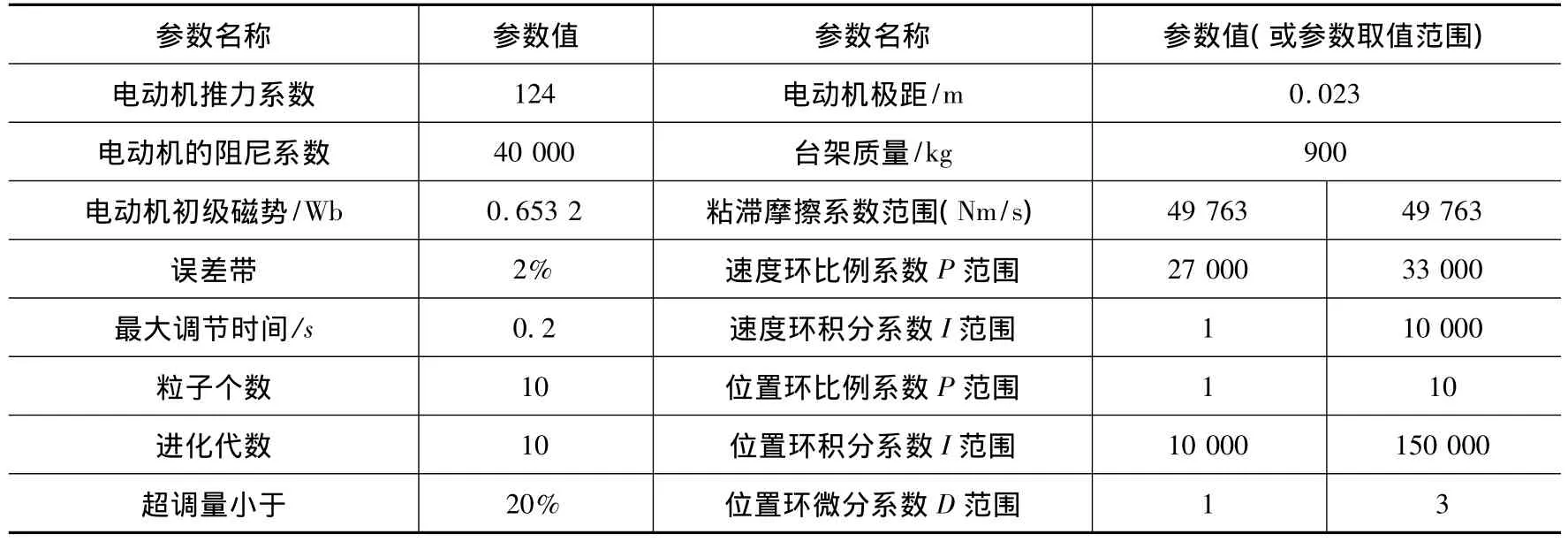
表4 原始参数值设置

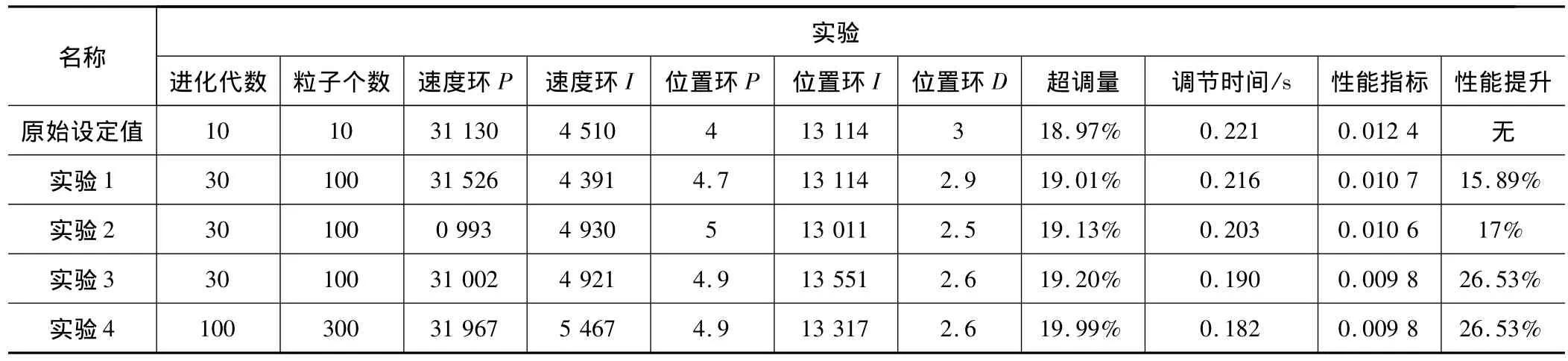
表5 多组仿真结果和实际机床参数对比

4 结语

(1)采用改进型粒子群算法，选择了最佳适应度函数，使用粒子群优化算法首次实现了被控对象传递函数中可变量及PID控制参数的同时优化。

(2)采用改进型粒子群算法对精密复合数控磨床伺服系统进行优化，在优化过程中，粒子群进化代数参数一般设置为100代，粒子个数设置为300个，得到的性能指标、调节时间和超调量等参数是理想的。

(3)通过实验对比分析，实验表明:该优化算法收敛性强。对系统同时使用多参数进行优化，大幅度提高了优化效率。优化后表征系统动态响应特性的性能指标有明显的提高，提高幅度可达到26.53%，且具有很高的实际应用价值。

(4)由于在实际中不能随意修改磨床机械参数，因此在实验中只对磨床伺服系统电参数进行了优化。对于车床制造商来说，可以将磨床机械参数与电参数一起进行优化，从而制造出性能更加优良的数控车床。

［1］彭浩.数控复合磨削技术的发展及研究现状［J］.航空制造技术，2010(10):54－57.

［2］胡蒲希，钱炜，陈靖菲.基于直线电动机伺服系统的数控铣削自适应控制系统的数学建模［J］.科学技术与工程，2011(4):838－840.

［3］Donaldson R R，Patterson S R.Design and construction of a large vertical axis diamond turning machine［C］.Lawrence Livermore National Laboratory Report，1983.

［4］文德.现代超精密加工技术的发展和应用［J］.世界产品与技，1998(3):10－12.

［5］袁哲俊，周明.加速发展我国的精密和超精密加工技术［J］.工具技术，1994(2):17 －22.

［6］叶云岳.国内外直线电机技术的发展与应用综述［J］.电器工业，2003(1):12－16.

［7］秀欣，马同禄.直线电机及其应用简介［J］.机械工程师，2003(9):95－96.