洪水作用下丁坝可靠度分析及剩余寿命预测

韩林峰，王平义，刘怀汉，杜 飞

(1．重庆交通大学 河海学院，重庆 400074;2．长江航道规划设计研究院，湖北 武汉 430011)

航道整治成败的关键在于治理效果，而整治建筑物的稳定性是确保治理效果的重要基础．在所有结构工程领域，运用可靠度理论和方法进行分析和设计已成为一种趋势．与岩土、土木、水利等建筑物破坏形式不同，航道整治建筑物破坏因素极为复杂［1－3］:一方面，整治建筑物密实度较差、结构强度低、基础可动性强;另一方面，水流、河势等外部因素变化大，加之其工作环境一般位于水下，条件复杂且难以进行实际观测．正是由于影响整治建筑物破坏的因素尚不明确，对其水毁机理的认识不够深入，因此尚未形成公认的整治建筑物失稳破坏计算模型和极限状态方程，对于局部稳定的验算尽管规范中有计算公式，但由于经验性较强，往往计算值与实际情况有较大偏差，使得可靠度计算方法在整治建筑物中的应用缺乏必要的理论基础．目前整治建筑物的设计仍采用传统的单一安全系数法，未考虑设计变量中客观存在的变异性，因而不能全面准确地反映整治建筑物的可靠性．基于现阶段国内外对整治建筑物可靠性及其使用寿命的研究寥寥无几，因此如果能够从整治建筑物的破坏机理出发，在充分考虑设计变量随机性的基础上分析整治建筑物的可靠度显得尤为重要．

本文以整治建筑物中最常见的丁坝为研究对象，通过原型观测和水槽试验，发现丁坝水毁主要是由于洪水涨退时坝体遭受洪水冲击破坏，以及水流挟沙力增强导致坝头附近冲刷坑增大使得坝体由于自身重力作用而导致的失稳坍塌破坏．洪水作用下丁坝的破坏，从几何结构角度来看，原坝体结构发生变形破坏并形成新的稳定结构;从力学性能上来看，新结构的结构抗力、阻水能力等均有所降低．借鉴损伤力学中的宏观分析方法，引进损伤变量(本文指水毁体积)作为内部变量［4］，通过宏观现象分析坝体水毁过程，并由此建立丁坝水毁的本构关系．

1 洪水条件下丁坝可靠度分析

1．1 洪水循环破坏试验设计

每次洪水的洪峰流量、洪水总量、洪水过程线形状等各不相同，每年发生的洪水次数、历时又各不相同．考虑到实际洪水过程与丁坝水毁之间的关系十分复杂、可变因素较多，因此本次水槽试验采用概化高斯曲线来模拟洪水过程．

根据长江重庆航运工程勘察设计院提供的“长江中游荆江河段已建航道整治建筑物现状调查及损毁原因分析”专题研究报告中的三峡水库蓄水后坝下游宜昌、枝城、沙市、监利、螺山、汉口等站历年洪水资料，分析各次洪水的最大洪峰流量及其对应的实测最大流速，并将其按照发生的频率及流量大小分成不同的洪水段，再通过比尺换算到水槽试验中来，可以算出试验中洪峰流量在38．7～100 L/s范围内的分布，找出几次发生频率较大且有代表性的洪水，其洪峰流量分别为38．7，50，68和100 L/s，并将洪水过程概化成高斯曲线(见图1)．水槽试验是在重庆交通大学国家内河航道整治工程技术研究中心航道整治试验大厅长30 m、宽2 m、高1 m的矩形玻璃水槽中进行，最大可产生近0．2 m3/s的流量．本次试验的坝体结构是长江中下游常见的正挑梯形断面抛石丁坝，迎水坡坡度为1∶1．5，背水坡坡度为1∶2，向河坡为1∶5，试验采用1∶60的正态模型．

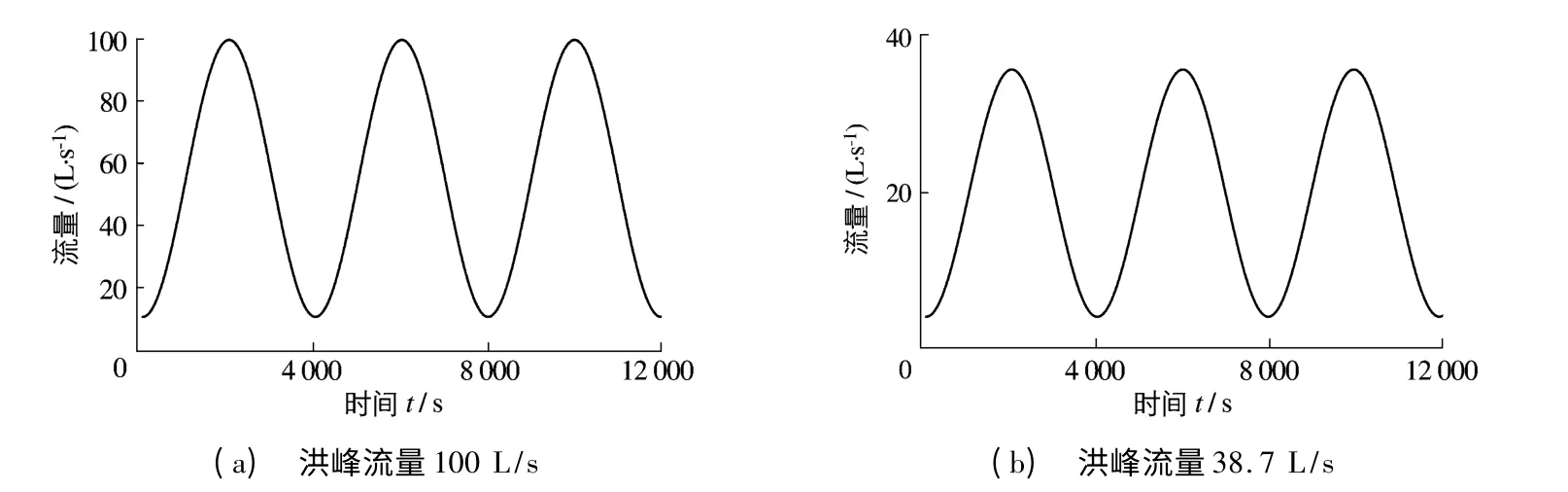
图1 水槽试验概化洪水过程曲线Fig．1 Generalized flood curves given by flume experiment

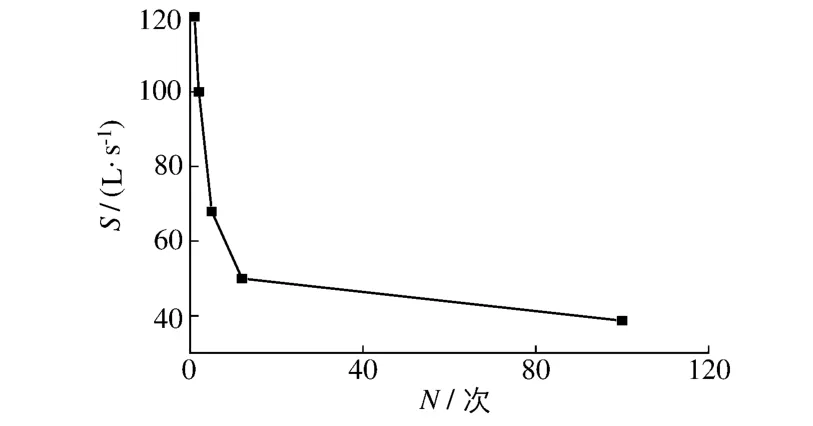
图2 洪峰流量S与水毁循环次数N的关系Fig．2 Relationship between flood peak discharge S and water-damage cycle times N

天然河道中每一次的洪水历时都不相同，但本次试验为了找出丁坝在不同洪峰流量下的水毁过程，将不同洪峰流量下每次洪水循环历时视为相同，即ti－ti－1=C(C为常数)．设S为最大洪峰流量，N为使丁坝水毁以至于无法满足整治要求时的洪水循环次数(丁坝洪水循环使用寿命)．从水槽试验中得到，当最大洪峰流量为38．7，50，68，100和120 L/s(依次为工况1～5)时，经洪水循环作用丁坝水毁体积达到坝头总体积30%时洪水循环次数分别为100，12，5，2和1．试验中当洪峰流量为38．7 L/s时，无论循环多少次丁坝水毁体积都达不到30%，因此以100次来表示;这里的120 L/s是为了应对将来有可能发生的超大洪水而进行的模拟性试验．由此得到坝体水毁S－N关系曲线，如图2所示．

这里需要说明的是丁坝作为最常见的一种河道整治建筑物，在建成投入使用一段时间后，坝体会出现不同程度的水毁，但以往经验表明并不是只要丁坝发生损坏就一定失去其整治功能，有时坝体虽部分水毁但仍可以满足整治要求．究竟丁坝水毁程度为多少时认为其失效，航道部门一直没有给出明确的规定．本文通过在清水冲刷试验中对坝头断面平均流速与坝体水毁体积的跟踪测量，提出以丁坝水毁体积V1与坝头总体积V0的比值V1/V0为表征丁坝水毁程度的指标，并认为当丁坝水毁体积达到坝头总体积的30%时丁坝失效，即当V1=0．3V0时的水毁体积为临界失效水毁体积．

选择30%作为丁坝失效的临界值，其原因在于清水冲刷试验中，对某一工况下丁坝坝轴线断面上远离坝头10 cm处的断面平均流速进行跟踪，从水流调稳时开始，到坝体水毁体积大约达到坝头总体积的30%左右时结束，此时坝头最大平均流速约减小50%(图3)．而在整治工程中丁坝的主要作用为束水攻沙﹑稳定航槽，随着坝头处流速的减小，丁坝渐渐达不到整治要求，因此认为当丁坝水毁体积达到坝头总体积的30%时，丁坝失效．试验中对水毁体积的测量是在每一次洪水周期过后，在ti(i=1，2，3，…)时刻将每一次洪水循环后的水毁体积Vi叠加，求出=0．3时，记下在此洪峰流量下的洪水循环次数N，其中为累计水毁体积．

1．2 洪水循环可靠度模型

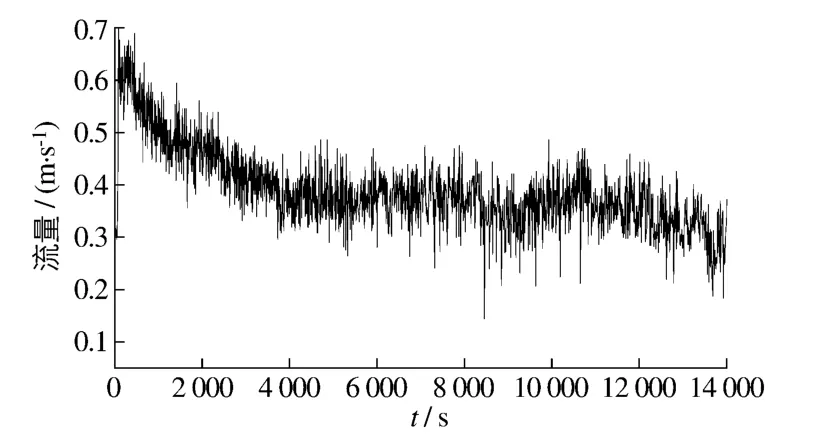
图3 某一工况时的跟踪流速Fig．3 Tracking velocity diagram under a working condition

由于散抛石坝的结构松散度较大且坝基处泥沙运动的随机性导致丁坝的水毁S－N关系也有明显的随机性．假设f(N)为在确定洪峰流量S下，丁坝水毁体积达到坝头总体积的30%时的洪水循环次数N的密度函数，由于天然条件下丁坝周围水沙条件复杂，坝体多以抛石为主，密实度较差，加之其工作环境一般位于水下，难以进行实际观测，所以丁坝受洪水冲击作用下的失效模型究竟服从何种分布，目前还没有充足的论证，也难以从理论上推断究竟服从何种分布．对工况3和4(最大洪峰流量为68和100 L/s)分别进行12次洪水循环作用下坝体破坏试验，得到的试验结果如图4所示．

图4曲线类似于某种指数形式或极值形式的分布函数，但由于本文中的数据是从概化水槽模型试验中得到的，加上样本数量较少，而建模成败的关键是要选择恰当的寿命分布类型，盲目地依赖于假设检验是不可取的［4］，因此通过图4曲线并不能准确地得到洪水循环作用下丁坝的水毁失效分布模型．但考虑到曲线的形状及工程上常采用的寿命分布形式［6］，本文借鉴损伤力学中通过定义损伤变量研究损伤演化规律来预测疲劳寿命的方法以及混凝土冻融循环作用下的失效分布模型［7］，提出一种应用比较普遍的三参数威布尔(Weibull)分布模型对洪水循环作用下丁坝可靠度进行探究．之所以选择威布尔分布是由于威布尔分布对于各种类型的试验数据拟合的能力很强，在各个领域中有许多现象近似地符合于威布尔分布，它的适用范围很广，是在可靠性工程中广泛使用的连续型分布形式［8］．选择Weibull分布的另一个原因是［4］:无论指数分布还是极值分布都与Weibull分布密切相关;在大量仿真试验的基础上发现正态分布和三参数威布尔分布之间存在解析关系;工程中常常可以用威布尔分布有效地拟合对数正态数据，用三参数威布尔分布拟合正态和对数正态数据，相对误差ε＜5%．由此可见，用三参数威布尔分布拟合试验数据，可以提供工程上能够接受的统一结果．

通过以上的分析，本文拟采用比较普遍的三参数威布尔分布对丁坝坝体可靠度进行推导，首先建立洪水循环作用下丁坝的寿命分布函数:

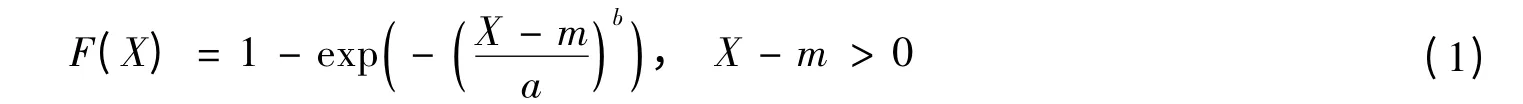
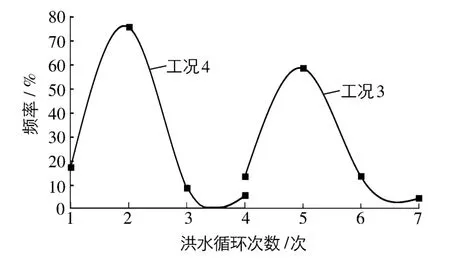
图4 丁坝失效时洪水循环次数－发生频率曲线Fig．4 Flood cycles and frequency of occurrencecurve during spur dike failure

式中:X为寿命随机变量;m为最小保证寿命;a为特征寿命或尺度参数;b为形状参数．

相应的丁坝受洪水循环作用寿命分布密度函数可表示为

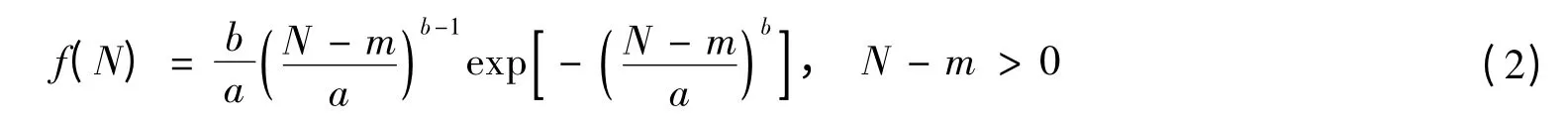
已知洪峰流量和丁坝受洪水循环作用寿命分布密度函数，则可得丁坝在洪水循环作用下的可靠度为

式中:n为给定的洪水循环次数;Pr(N)为在洪水循环次数n下的可靠度．

由式(2)和(3)可知洪水条件下丁坝坝体可靠度为

1．3 不同洪峰流量时洪水循环作用下各阶段丁坝失效概率

如图2所示，在洪水历时相同情况下，最大洪峰流量对丁坝水毁程度影响很大，当洪峰流量为38．7 L/s时，坝体失效(水毁体积达到总体积的30%)洪水循环次数为100次，而当洪峰流量为120 L/s时，坝体失效洪水循环次数为1次．由于在真实河道断面上每一次洪峰流量、洪水总量等可能都各不相同，为了简化计算，假设将洪峰流量、历时相近的洪水循环归并为一个阶段，这样就把不同洪峰流量的洪水随机作用下丁坝的水毁问题简化为不同洪水段的洪水顺序作用下丁坝水毁失效问题．设第i阶段中洪峰流量为Si，洪水循环次数为ni，在这样的洪水循环作用下丁坝的使用寿命为Ni．为了便于分析，本文作了如下假设:(1)对于任一给定的洪峰流量，在每一次洪水周期作用后，坝体水毁体积相同;(2)不同洪峰流量的洪水施加顺序对丁坝使用寿命没有影响．

图5 洪水循环等效水毁关系Fig．5 Equivalent relationship of water-damage under the cyclic action by flood

由假设(1)可得，在水平Si下，洪水循环ni次产生的损伤因子(水毁程度)可以定义为Di=ni/Ni，当ni=Ni时，Di=1，坝体水毁体积达到坝头总体积的30%时，认为丁坝失效．在Si水平洪水循环作用下，洪水循环次数与丁坝坝体水毁程度成线性关系(如图5)．在Si水平洪水循环作用ni次，可以等效为在Sj水平下作用ni，je次洪水循环(如图5)．

由假设(2)可知，丁坝累计损伤程度只与洪水大小有关，而与施加顺序无关，虽然这与实际情况有所出入，但通过试验结果来看，在不同的洪水施加顺序下坝体累计水毁体积相差并不大(试验中小于7%)，因此我们认为此假设能够满足实际需要．对于丁坝来说，随着使用年限的增加，如果没有进行及时修补，其失效概率逐年递增，根据三参数威布尔分布的性质可得［6］，失效概率递增时，形状参数b＞1．

根据文献［7］对混凝土结构在冻融作用下各阶段失效概率的推导方法，本文尝试对洪水循环作用下，丁坝在各阶段的失效概率进行推导．由失效概率和可靠度的关系可得受洪水循环作用的丁坝失效概率为

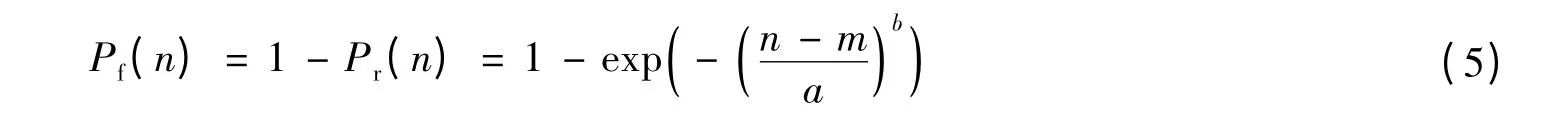
在第一阶段洪水循环作用下丁坝寿命的密度函数为f1(N1)，洪水循环次数为n1，可知这时丁坝失效概率为

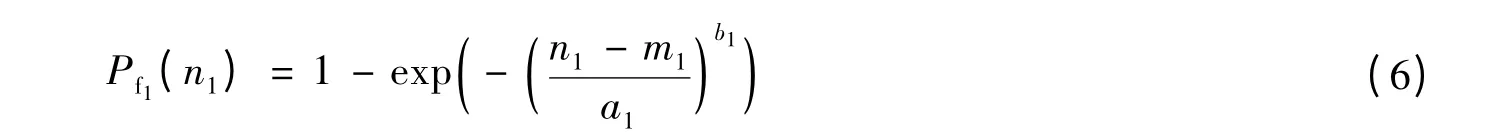
假设在第二阶段洪水循环作用下丁坝寿命的密度函数为f2(N2)，洪水循环次数为n2，那么可根据上述丁坝水毁等效原理将第一阶段洪水循环次数n1化成第二阶段的等效洪水循环次数n1，2e，使得在第一阶段洪水循环作用n1次坝体结构失效概率与在第二阶段洪水循环作用n1，2e次的失效概率相等，即有

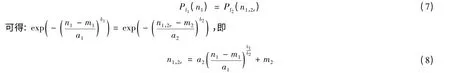
因此，在相邻的两阶段不同洪峰流量洪水循环作用下坝体结构的失效概率为

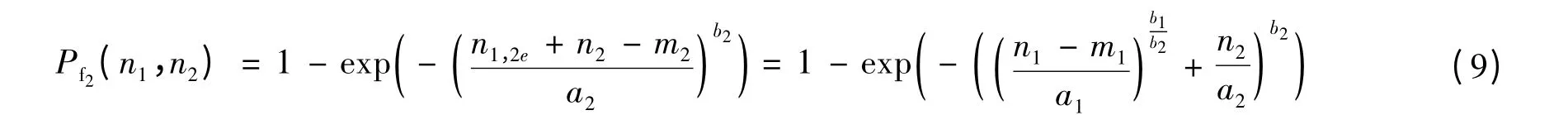
同样可将n1，2e+n2等效成第三阶段洪水循环作用下的等效循环次数n1+2，3e，类似于式(8)，可得

在相邻的3个阶段不同洪峰流量洪水循环作用下丁坝的失效概率为

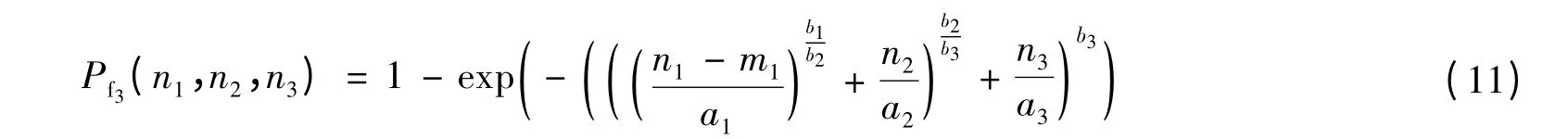
以此类推可得到在第k阶段作用下前k－1阶段洪水循环作用的等效循环次数为

在连续的k个阶段洪水循环作用下丁坝的失效概率为

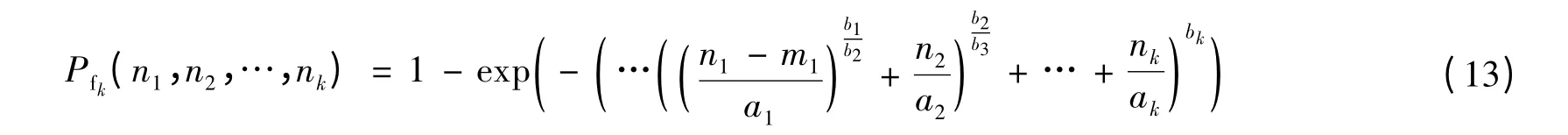
1．4 洪水作用下丁坝可靠度分析实例

通过上述理论来计算一个工程实例．某河段上一丁坝竣工后共经历了3次洪水作用，经分析该丁坝经历的3次洪水过程可以归结为两阶段洪水循环作用，试分析该丁坝的失效概率．本例中最小保证寿命m取0，各阶段参数见表1．

表1 丁坝受洪水循环作用各阶段分布函数的参数Tab．1 Parameters of distribution function in each stage under the cyclic action by flood

对于丁坝可靠度模型中的参数，由于实测资料有限，加上本文是首次提出洪水条件下丁坝的三参数Weibull可靠度模型，因此无法从其他的Weibull分布参数表中查找．根据表1的数据，这里我们选择一种针对小样本情况下对威布尔分布参数进行估计的一种方法——最优线性无偏估计法(BLUE)［9］．

此时对于式(1)中的丁坝受洪水循环作用的寿命分布函数，令X=lnN，则X服从极值分布，其分布函数为

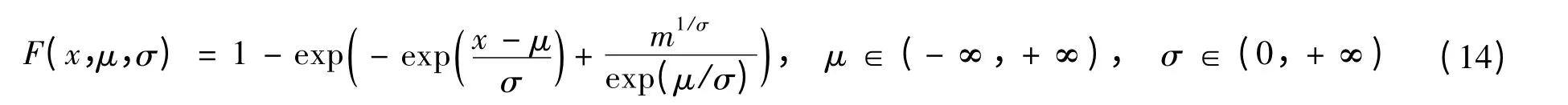
式中:μ，σ分别为极值分布的位置参数和尺度参数，且μ=lna，σ=1/b．当m=0时，有

利用BLUE方法对图4中的数据进行处理，获得母体分布参数和可靠性指标的估计，由BLUE无偏系数表，经计算后可得到坝体水毁分布参数的估计值(见表1)．

对于其他洪峰流量下的洪水循环分布参数，我们可以通过今后的工作，进一步进行统计，以建立起三参数威布尔丁坝可靠度模型的参数表，进而通过式(11)和(13)计算三阶段与k阶段的洪水循环作用下的丁坝失效概率．

2 经一定洪水循环作用后丁坝剩余寿命预测

实际河道中的丁坝，在服役期间一直遭受水流冲击作用，但并不是坝体一旦遭受洪水作用就会失去其整治能力，而是坝体先部分破坏，剩下的部分又重新形成新的稳定结构，仍能继续工作和承受下一次洪水的作用，直到坝体水毁体积达到一定程度．考虑到在实际工程中维持航道整治的效果比重新对其进行治理更为重要，因此在丁坝承受一定次数的洪水作用后，估算其还能再承受多少次洪水作用从而来预测丁坝的剩余寿命以便及时对其进行维修，对维护航道整治效果有重要的作用．

下面以两阶段洪水循环作用为例说明丁坝剩余寿命的预测过程．设在第1阶段，洪峰流量为S1下的洪水循环次数为n1，第2阶段洪峰流量为S2下的洪水循环次数为n2．在这两阶段不同洪峰流量的洪水循环作用下丁坝的剩余寿命计算步骤如下:(1)计算n1相当于S2水平下的洪水循环次数n1，2e，可由式(8)得到;(2)计算丁坝经历第二阶段洪水循环作用后的剩余寿命nr，可写成

对于更多阶段的洪水循环情况下的剩余寿命预测的计算过程可依此类推．仍以本文1．4节的例子进行剩余寿命预测，在经历了第2阶段的洪水循环作用后，丁坝的剩余寿命为nr=5－2．87－2=0．13，即此丁坝还可以承受S2水平的洪水作用0．13次，也就是1次．基于目前国家水文预报已趋于成熟，可以通过对河道中每年的洪水预报来计算丁坝的剩余寿命．如预测到明年S2水平的洪水将会发生，则此丁坝剩余使用寿命为1年;如果为Si水平的洪水，则可以通过等效循环次数的计算公式，计算出坝体还可以承受Si水平的洪水循环次数．经实地勘测，在经过两阶段洪水循环作用后，该丁坝的水毁体积达到坝头总体积的25．48%，而在经过下一年一次S2水平的洪水作用后水毁体积达到坝头总体积的32．6%，通过前文对坝体失效的定义可以看出该丁坝已经失效，从预测结果来看，用丁坝剩余寿命计算公式得到的结果与实际情况较为相符．

3 结语

(1)借鉴损伤力学中的宏观分析方法，基于三参数Weibull分布，建立了洪水作用下丁坝可靠度分析模型，利用水毁等效原理，推导出丁坝受洪水循环作用下失效概率计算式，该计算式形式简单，便于应用．

(2)结合洪水作用下丁坝可靠度分析模型，通过论证和推导，得出了洪水作用下丁坝剩余寿命计算式，结合现代水文学中的洪水预测机制，可以得出在遭受一定洪水作用后丁坝的剩余使用年限，对维护航道有重要意义．

(3)本文通过水槽试验对抛石丁坝坝头断面平均流速与坝体水毁体积进行跟踪测量，首次提出以坝体水毁体积达到坝头总体积的30%为临界失效水毁体积，为抛石丁坝安全性的判别提供依据．

(4)对于采用Weibull分布来描述洪水作用下丁坝的失效模型是否正确还有待于通过大量的原型资料来进一步验证．由于本文的数据都是从水槽试验中得到的，虽然模型通过一定的比尺来控制，但毕竟概化水槽无法真实模拟天然河道中的水沙及边界条件，而且试验中的概化洪水过程也不能完全反映天然的洪水过程，因此接下来可以进一步分析在实际洪水过程下丁坝的水毁情况，尝试找出其水毁规律．

［1］王平义，程昌华，荣学文，等．航道整治建筑物水毁理论及模拟技术［M］．北京:人民交通出版社，2005．(WANG Pingyi，CHENG Chang-hua，RONG Xue-wen，et al．The water damage theory of waterway regulation structure and simulation technique［M］．Beijing:China Communications Press，2005．(in Chinese))

［2］YU Tao，WANG Ping-yi，YANG Cheng-yu，et al．Experimental study of water force acting on spur dike［J］．Advances in Civil Engineering，2011:3558-3562．

［3］XU Ge-ning，YANG Rui-gang，ZHOU Ke，et al．Methodology to estimate remaining service life of steel structure by possibilistic reliability theory［J］．Chinese Journal of Mechanical Engineering，2010，23(6):780-787．

［4］邬华芝，郭海丁，高德平．疲劳破坏寿命的概率统计方法研究综述［J］．强度与环境，2002，29(4):38-43．(WU Huazhi，GUO Hai-ding，GAODe-ping．Generalization of life characteristic investigation for probabilistic fatigue failure［J］．Structure＆Environment Engineering，2002，29(4):38-43．(in Chinese))

［5］曹艳敏，张华庆，蒋昌波，等．丁坝冲刷坑及下游回流区流场和紊动特性试验研究［J］．水动力学研究与进展:A辑，2008，23(5):560-569．(CAO Yan-min，ZHANG Hua-qing，JIANG Chang-bo，et al．The experimental research of the flow field and turbulence characteristics in the scour and backflow region around a groin［J］．Chinese Journal of Hydrodynamics(SerA)，2008，23(5):560-569．(in Chinese))

［6］PRABHAKAR MURTHY D N，BULNER M，ECCLESTON JA．Weibull model selection for reliability modeling［J］．Reliability Engineering＆System Safety，2004，86(3):257-267．

［7］宋玉普，冀晓东．混凝土冻融损伤可靠度分析及剩余寿命预测［J］．水利学报，2006，37(3):259-263．(SONG Yu-pu，JI Xiao-dong．Analysis of reliability of concrete under freezing thawing action and evaluation of residual life［J］．Journal of Hydraulic Engineering，2006，37(3):259-263．(in Chinese))

［8］幺亮，冯蕴雯．三参数威布尔分布疲劳寿命分散系数确定方法［J］．科学技术与工程，2009，9(6):1488-1493．(YAO Liang，FENGYun-wen．Fatigue life scatter factor conformation method for sample follows the three parameters Webull distribution［J］．Science Technology and Engineering，2009，9(6):1488-1493．(in Chinese))

［9］张志华．可靠性理论及工程应用［M］．北京:科学出版社，2012．(ZHANG Zhi-hua．Reliability theory and engineering application［M］．Beijing:Science Press，2012．(in Chinese))

［11］LEE E T，WANG J．Statistical methods for survival data analysis［M］．America:Wiley，2003．

［12］茆诗松，周纪芗，陈颖．试验设计［M］．北京:中国统计出版社，2004．(MAO Shi-song，ZHOU Ji-xiang，CHEN Ying．Experiment design［M］．Beijing:China Statistics Press，2004．(in Chinese))

［13］长江航道局．航道工程手册［M］．北京:人民交通出版社，2004．(Changjiang Waterway Bureau．Waterway engineering handbook［M］．Beijing:China Communications Press，2004．(in Chinese))