浯溪口水利枢纽溃坝洪水模拟

石 莎，范子武，张 铭，费香波，乌景秀

(南京水利科学研究院，江苏 南京 210029)

浯溪口水利枢纽位于景德镇市蛟潭镇境内，距景德镇市区40 km，是昌江干流中游一座以防洪为主，兼顾供水、发电等的综合利用工程．水库总库容为4．27亿m3，大坝坝长538．4 m，最大坝高45．6 m，正常蓄水位56 m，设计洪水位62．3 m，校核洪水位64．3 m．工程等别为二等，非溢流坝、溢流坝、河床式厂房(挡水部分)等主要建筑物的级别为2级，次要建筑物为3级，临时建筑物为4级．混凝土坝防洪标准采用100年一遇洪水设计，1 000年一遇洪水校核;土坝防洪标准采用100年一遇洪水设计，2 000年一遇洪水校核．

浯溪口水利枢纽工程坝址下游的主要防洪保护对象是景德镇市．景德镇市2010年城市建设用地面积72．84 km2，总人口46．21万，工业总产值369．61亿元．浯溪口水利枢纽建成后，通过浯溪口水库与景德镇市城防工程联合调度，可以使景德镇市区的防洪标准提高到50年一遇设防标准．但是，水库大坝自身安全性所导致的溃坝洪水将给下游地区带来潜在风险［1-2］．因此对浯溪口水利枢纽溃坝洪水演进的模拟计算对于其下游防洪，特别是景德镇市的防洪管理决策具有十分重要的意义．

基于溃坝水流的破坏性和溃坝后果的严重性，世界各国高度重视大坝的安全问题．自19世纪以来，各国学者分别从理论分析、物理模型试验、数值模拟、溃坝洪水演进模型研究、历史资料统计分析等方面对溃坝问题进行了系统研究［3］．其中，物理模型试验和数值模拟是近几十年来应用较多的研究方式．然而，溃坝洪水的物理模型试验耗资高，且操作上具有一定的技术难度，因而目前数值模拟在溃坝洪水演进方面是较常用的研究手段．溃坝的速度和程度决定了溃坝洪水的大小和传播速度，从而影响了溃坝洪水的影响范围和程度［4］．溃坝水流的流态十分复杂，在洪水演进过程中，通常伴随着急流、缓流和临界流的情况［5］．因而构建合理的溃坝洪水演进数学模型，计算溃坝洪水的淹没范围、水深和到达时间等要素，能为建立溃坝风险图和评估溃坝损失提供科学依据，从而对水库和堤防失事影响做出定量估算，并合理确定水库或堤坝防洪设计标准及避险措施［6］．

TELEMAC-2D是一款基于有限单元法求解二维浅水方程的开源软件，可以用于研究风暴潮、河流海岸动力学、波的传播、泥沙和污染物输移等，其网格划分为非结构化三角形网格，对于重要区域可进行局部加密．TELEMAC-2D在西欧、加拿大和美国等地区与国家河流模拟中应用较为广泛［7-12］．此外，加拿大学者D．Lam等在所研究的多模型集成决策支持系统中应用TELEMAC-2D模拟湖流部分［13］．德国学者将TELEMAC-2D应用于洪水污染研究、海啸对德国沿岸城市影响研究以及河口支流水流流态研究等［14-16］．西班牙学者应用TELEMAC-2D研究了沉水植物对水流阻力及涡黏性的影响［17］．荷兰学者应用TELEMAC-2D研究了Belgium的Ijzer河口的水动力学及泥沙输移［18］．法国学者应用TELEMAC-2D对鱼道水力学特性进行了研究［19］．英国学者将TELEMAC-2D作为有限单元法代表性软件与有限差分法进行了对比性研究［20］．TELEMAC-2D在中国的应用则比较少，可查文献有中国学者Zhang Cheng应用TELEMAC-2D对云南洱海的二维湖流进行研究［21］，童朝锋等应用TELEMAC-2D系统建立长江口盐水数值模型计算了不同径流、潮汐条件下，崇启大桥桥墩区域的潮位和盐度变化过程［22］．

本文应用TELEMAC-2D建立浯溪口下游洪水演进二维数学模型，对浯溪口坝址下游河道洪水演进进行模拟，采用河道水面线和河道断面水位流量过程线验证模型合理性，并且将几组不同重现期的溃坝流量作为上游边界条件，对浯溪口水库下游二维溃坝洪水演进进行了数值模拟，计算了昌江河道不同断面的流量水位变化过程、洪水是否漫堤和洪水到达的时间等要素，为洪水风险评估提供了科学依据．

1 数学模型

TELEMAC系统基于有限元数值求解程序，包含了明渠流的数字绘图等普通功能．研究范围覆盖了水动力学、波、输移质、地下水和水质等．TELEMAC-2D作为TELEMAC系统中的一个计算模块，其计算基于Saint-Venant方程组，由Navier-Stokers方程组垂向积分再取平均所得．方程采用有限单元法进行求解，其中对于非线性项采用了相应的假定和近似法［23］．应用TELEMAC-2D所建立的浯溪口水利枢纽下游二维溃坝洪水演进数值模型如下．

1．1 基本方程

基本方程为垂向平均的Navier-Stokers方程组．

式中:h为水深;u，v分别为x，y方向的速度;g为重力加速度;νt为动力扩散系数;z为自由表面高程;t为时间;Sh为水流源或汇;Sx，Sy分别为动力方程的源或汇;div(*→)为散度;▽→(*)为梯度．

1．2 边界条件确定及参数选取

TELEMAC-2D中采用关键字定义计算参数、边界条件和初始条件等．对于浯溪口溃坝洪水二维演进数学模型，边界条件类型数据存储于文件名为*．lci的边界条件文件中，4个整型:LIHBOR，LIUBOR，LIVBOR和LITBOR，它们分别有0～6共7个取值，每个取值代表不同的边界类型．此文件由JENAT软件生成．TELEMAC-2D的求解是基于特征曲线法，应用中要求在流体边界的每个点都给出变量h，u，v的具体情况，TELEMAC-2D中的原则是:(1)急流入口，给定流速和水深;(2)缓流入口，给定流速和自由水深;(3)急流出口，自由流速和自由水深;(4)缓流出口，自由流速和给定水深．在浯溪口二维溃坝洪水数学模型中，上边界为流量过程边界，LIHBOR=4(自由水深的开边界)，LIUBOR/LIVBOR=5(给定流量过程的开边界)，此处不考虑污染物情况，因此LITBOR不进行赋值．下边界为水位边界，LIHBOR=5(给定水深的开边界)，LIUBOR/LIVBOR=4(自由流速的开边界)，同样不考虑污染物情况，因此LITBOR不进行赋值．

而边界条件中的具体数据，分别存储于文件名为*．lbf的文件(上边界为流量过程边界:不同重现期下浯溪口溃坝洪水流量过程)中和文件名为*．qz的文件(下边界为水位过程:昌江下游断面的水位-流量关系特性曲线)中．计算时分别在配置文件(*．str)中取关键字LIQUID BOUNDARIES FILE=*．lbf，STAGEDISCHARGE CURVESFILE=*．qz和STAGE-DISCHARGE CURVES=0(或1)，即可调用文件中准备好的流体边界数据．关于固壁边界关键字取值为LAW OF BONTTOM FRICTION=2，表示采用Chezy公式，FRICTION COEFFICIENT=50．初始条件对应关键字取为INITIAL DEPTH=0．01计算时步采用变步长，初始时步给定为TIME STEP=10，采用变时步关键字为VARIABLE TIME-STEP=YES，总计算时长根据溃坝流量过程定，关键字取值为DURATION=500 000(计算时步所有取值单位均为s)．

1．3 计算区域确定及网格划分

如图1所示，计算区域以60 m等高线为界，模型上游入口为浯溪口大坝坝址处，下游出口距上游入口62 km．渡峰坑位于景德镇市西郊垦殖场庄下村，景德镇城区在渡峰坑上游约3．7 km处．

本文采用JANET软件进行网格划分和网格质量检验．全区域为三角形单元，河道局部加密，满足河道横断面至少5个计算节点的要求．整个区域总计28 542个节点，56 428个单元．其中，最大长度673．6 m，最小长度21．5 m;最大面积158 848 m2，最小面积252 m2;最大角度123°，最小角度19°(见图1)．考虑到需要对各节点的高程数据进行插值，根据已知的等高线密度确定网格密度;JANET对网格质量检验合格，一个工况的计算耗时约2．5 h．

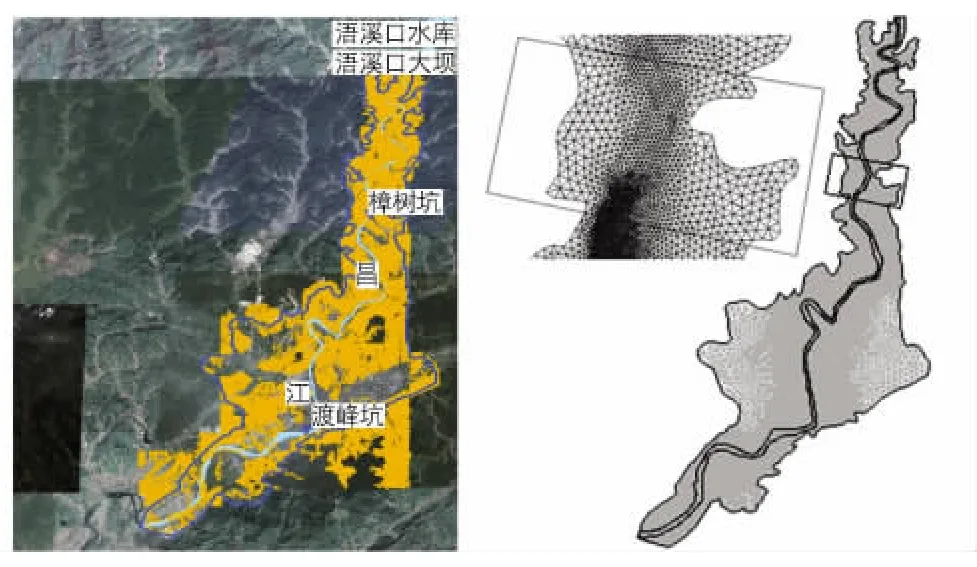
图1 模型区域及模型网格Fig．1 Model area and model mesh

2 模型验证

模型验证分为2个部分:一是以测量断面同期的实测水位为边界条件，对昌江纵断面水面线与实测水面线进行对比验证;二是对渡峰坑断面的水位流量关系曲线进行验证．

2．1 水面线验证

2009年3月至5月，景德镇市水文局在浯溪口坝址至渡峰坑的昌江段进行了断面测量，同时获得了对应时期的断面水位资料．本文以断面测量同期的实测水位为边界控制，计算得到昌江纵断面水面线，与实测水面线进行对比(见图2)，浯溪口坝址位于106 km处，下游延续到渡峰坑约62 km处．从图中可见，计算水面线和实测水面线之间有良好的拟合关系．上游偏差较大，是由于上游约100 km处有一拦水坝，对过水有短期的影响，造成实测水面线有比较明显的水头差．下游67 km左右有个水位陡降的过程，这是由于此处(渡峰坑上游不远处)有一支流汇入，对上游来水有一定顶托作用．但由于本次验证采用水位边界，流量较小，当流量较大时，昌江整体水位抬高，拦水坝的阻水作用将大幅减小．从验证结果看，浯溪口二维数值模拟所采用的基础数据，包括地形、断面均合理可靠．

2．2 渡峰坑断面水位流量关系曲线验证

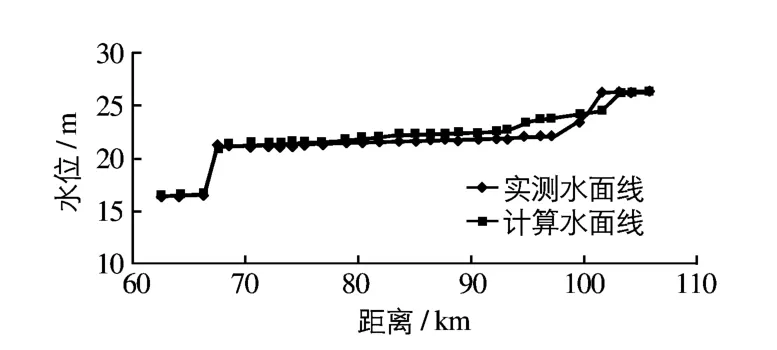
图2 昌江水面线对比Fig．2 Water surface profiles of the Chang River

渡峰坑水文站设立于1941年，流量资料最为齐全．因此模型采用渡峰坑断面水位-流量关系进行验证．上游边界为流量边界，下游取出口处水位-流量关系为下边界，进行模型计算．从计算结果中提取渡峰坑断面各个时刻的水位和流量数据，以流量为横轴、水位为纵轴绘制水位-流量关系，与渡峰坑断面的实测水位流量过程进行对比(见图3)．由图3可见，计算所得的水位-流量关系离散点均匀分布于实测水位流量关系点附近，并且几乎将实测水位-流量关系线包括其中．证明下游边界所取的水位流量关系是合理可靠的．由以上验证结果可知，TELEMAC-2D系统应用于浯溪口溃坝洪水演进二维数值模拟计算是合理有效的．

图3 渡峰坑断面水位-流量关系散点分布Fig．3 Water level-discharge curves

3 模型应用

3．1 设计洪水组合

由设计暴雨推求设计洪水的方法得到浯溪口水库的入库设计洪水，再与水库不同特征水位(设计洪水位62．3 m、校核洪水位64．3 m)进行组合，见表1．当水位超过设计洪水位，水库按泄洪能力泄流．采用改进的BREACH模型，考虑不同入库洪水重现期和特征水位，模拟计算出各种组合下浯溪口土坝坝段漫顶溃决溃口处流量过程，见图4，以此作为下游溃坝洪水演进数值模拟的上游边界条件．

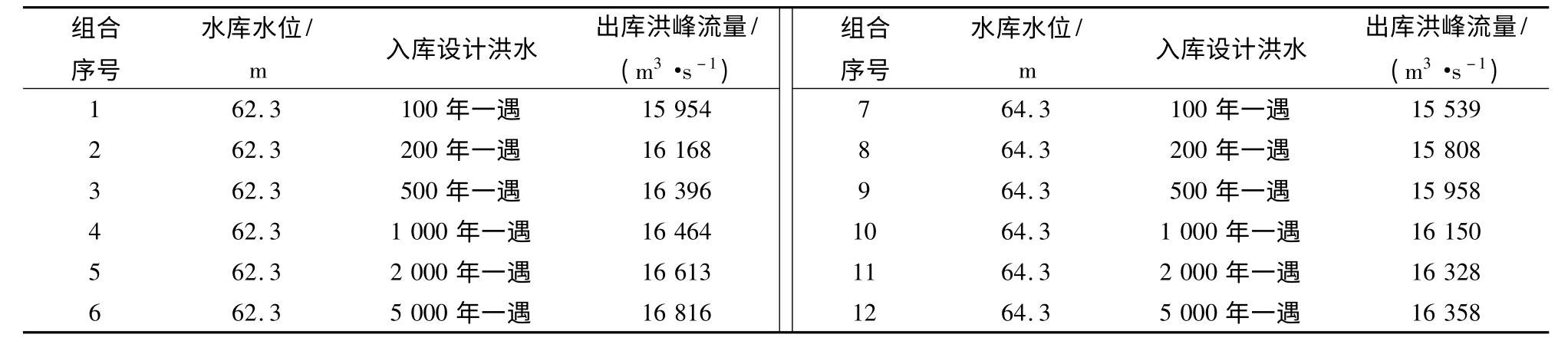
表1 模型计算组合Tab．1 Calculation combinations of the model

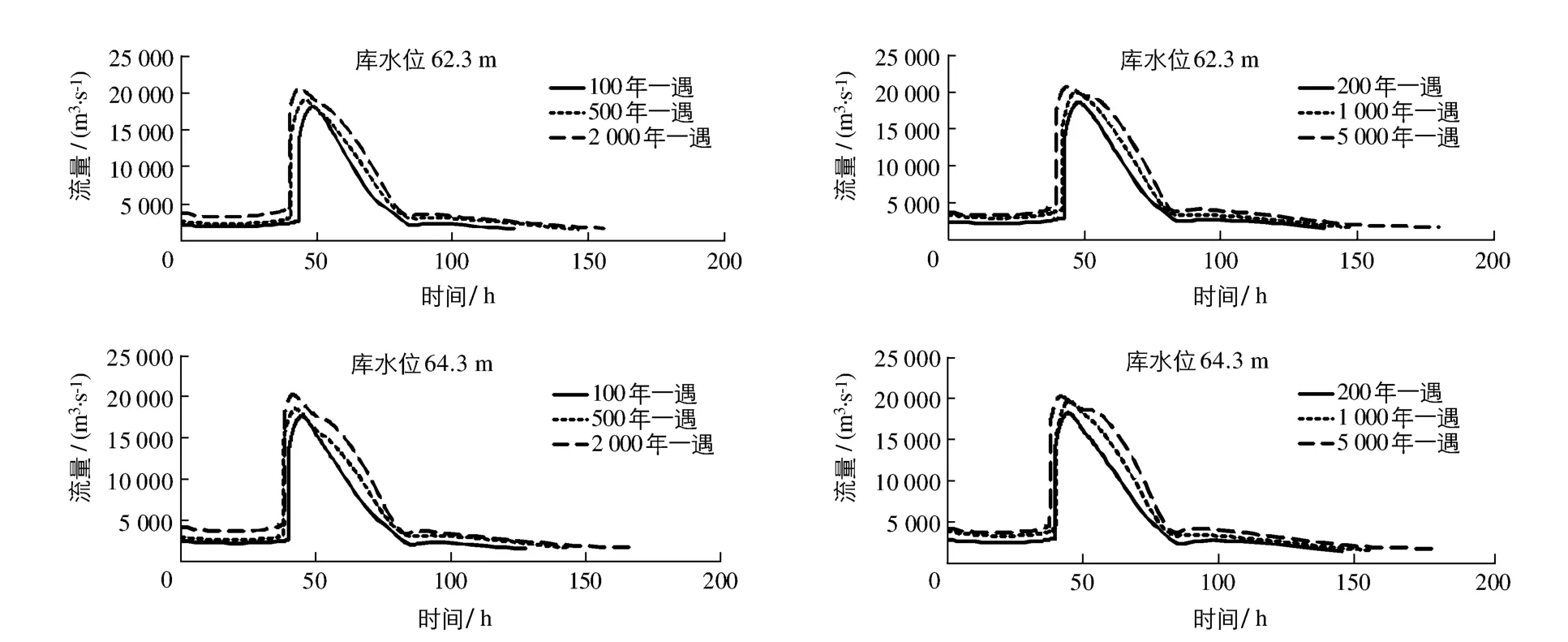
图4 不同工况下溃坝洪水过程Fig．4 Dam-break flood routing under different conditions

3．2 各种组合的计算结果分析

3．2．1 淹没特征值 表2为12种组合情况下大坝下游洪水演进特征值．由表可见，设计水位条件下的最大流速和最大水深均较校核洪水位时大，这是由于校核洪水位的溃坝发生时间较早，入库洪水还未达到洪峰流量时，溃坝洪水已经发展至洪峰，而入库洪水洪峰传递至坝址位置时，溃坝下泄流量已经错过洪峰值，此时的入库洪水流量与溃坝下泄流量进行叠加所产生的最大洪峰流量反而小于二者在设计洪水位时所对应的叠加洪峰流量．由图4中不同工况下溃坝洪水过程也可看出，溃坝洪水洪峰值会随着洪水重现期的增大而增大并且在发生时间上有所提前．此外，5 000年一遇校核洪水位和设计洪水位对应的最大淹没水深、最大流速和最大流量等特征数据均小于2 000年一遇．原因是当遭遇5 000年一遇特大洪水时，入库洪水与溃坝洪水的错峰更加明显，使得二者的洪量叠加所产生的洪峰小于遭遇2 000年一遇洪水时二者的叠加值．

表2 洪水演进特征参数Tab．2 Flood routing characteristic parameters

3．2．2 淹没范围 图5为组合3、9情况下浯溪口土坝坝段溃坝洪水的演进过程，黑色部分表示未被洪水淹没的陆地，白色部分为水淹部分，白色与黑色的递进表示水深逐渐减小．由图可见，下游淹没范围较大，景德镇城区也在淹没范围内，且积水较多．此外，由图5还能看出，随着时间的推移，洪峰流量由上游向下游传播，溃坝1 h至20 h小时过程中，溃坝水流流量越来越大．

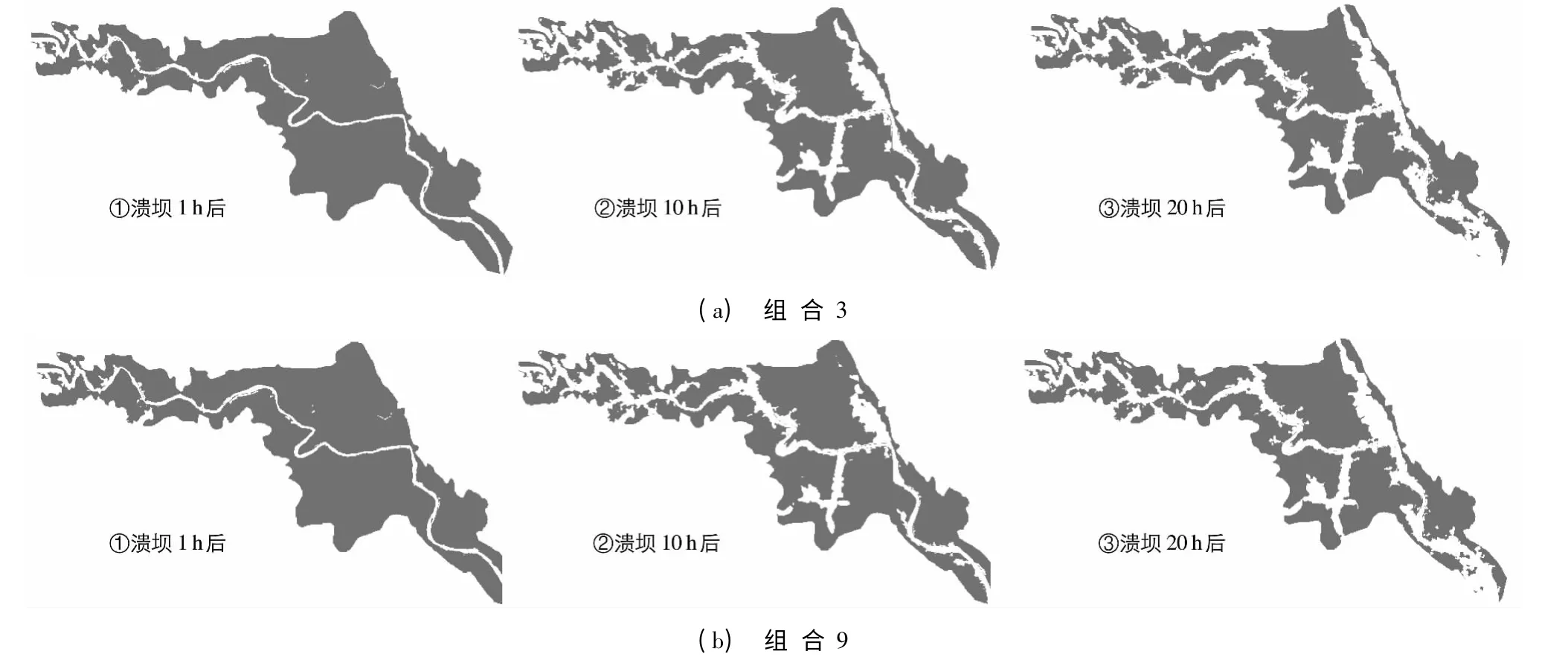
图5 两种组合下淹没范围对比Fig．5 Comparison of the flooded downstream areas under two conditions

4 结语

本文应用TELEMAC-2D对浯溪口下游二维溃坝洪水演进进行了数值模拟．通过对昌江纵断面水面线和渡峰坑断面的水位流量关系曲线验证计算，表明模型所选取的参数是合理的，TELEMAC-2D系统能较好地模拟二维溃坝洪水演进过程．利用该模型模拟计算了浯溪口水利枢纽建成后，遭遇100年一遇、200年一遇、500年一遇、1 000年一遇、2 000年一遇、5 000年一遇的入库洪水流量情况下，漫顶溃坝水流洪水演进的基本参数，结果显示:

(1)由于入库洪水与溃坝洪水叠加作用，时间上产生的错峰，使得校核洪水情况下特征参数小于设计洪水下的特征参数;洪水重现期高达5 000年一遇时，由于溃坝水流与入库水流的叠加作用，错峰明显，以至其相关特征数据小于2 000年一遇．

(2)对于同一设计水位情况下，洪水重现期越长，溃坝洪水在下游演进过程中的最大流速、最大流量、最大淹没水深和最大淹没面积都越来越大．

(3)500年一遇来流情况产生溃坝的下游洪水最大水深为30．87 m，此时昌江局部地区出现了洪水漫堤现象，因此沿昌江河堤的防洪能力，特别是景德镇城区的堤防防洪能力需要适当提高．

本文现阶段主要研究了漫顶溃坝洪水演进，为浯溪口下游防洪风险管理提供了一定的可靠的基础数据支持．若进一步研究渗透溃坝洪水演进，并将其结果与漫顶溃坝洪水进行对比，对防洪预报预警与洪水风险管理的意义更为重大．

［1］龙晓飞，高龙华．茜坑水库溃坝洪水数值模拟研究［J］．人民珠江，2011(2):42-44．(LONG Xiao-fei，GAO Long-hua．Dam-break flood routing simulation of Qiankeng reservoir［J］．Pearl River，2011(2):42-44．(in Chinese))

［2］张利民，徐耀，贾金生．国外溃坝数据库［J］．中国防汛抗旱，2007(增刊):2-7．(ZHANG Li-min，XU Yao，JIA Jinsheng．Foreign dam failure database［J］．China Flood and Drought Management，2007(Suppl):2-7．(in Chinese))

［3］李云，李君．溃坝洪水模型实验研究综述［J］．水科学进展，2009，20(2):304-310．(LI Yun，LI Jun．Review of experimental study on dam-break［J］．Advances in Water Science，2009，20(2):304-310．(in Chinese))

［4］朱勇辉，廖鸿志，吴中如．国外土坝溃坝模拟综述［J］．长江科学院院报，2003，20(2):26-29．(ZHU Yong-hui，LIAO Hong-zhi，WU Zhong-ru．Review on oversea earth-dam-break modeling［J］．Journal of Yangtze River Scientific Research Institute，2003，20(2):26-29．(in Chinese))

［5］张大伟，李丹勋，王兴奎．基于非结构网格的溃坝水流干湿变化过程数值模拟［J］．水力发电学报，2008，27(5):98-102．(ZHANG Da-wei，LI Dan-xun，WANG Xing-kui．Numerical modeling of dam-break water flow with wetting and drying change based on unstructured grids［J］．Journal of Hydroelectric Engineering，2008，27(5):98-102．(in Chinese))

［6］史宏达，刘臻．溃坝水流数值模拟研究进展［J］．水科学进展，2006，17(1):129-135．(SHI Hong-da，LIU Zhen．Review and progress of research in numerical simulation of dam-break water flow［J］．Advances in Water Science，2006，17(1):129-135．(in Chinese))

［7］BRIÈRE C，ABADIE S，BRETEL P，et al．Assessment of TELEMAC system performances，a hydrodynamic case study of Anglet，France［J］．Coastal Engineering，2007，54(4):345-356．

［8］ASARO G，PARIS E．The effects induced by a new embankment at the confluence between two rivers:TELEMAC results compared with a physical model［J］．Hydrological Processes，2000，14(13):2345-2353．

［9］WOLF J．Coastal flooding:impacts of coupled wave-surge-tide models［J］．Natural Hazards，2009，49(2):241-260．

［10］SYME W J，PINNELL M G，WICKSJM．Modelling flood inundation of urban areas in the UK using 2D/1D hydraulic models［C］∥8th National Conference on Hydraulics in Water Engineering，Australia．2004．

［11］JONESJE，DAVIESA M．Storm surge computations for the west coast of Britain using a finite element model(TELEMAC)［J］．Ocean Dynamics，2008，58(5-6):337-363．

［12］DI BALDASSARRE G，CASTELLARIN A，MONTANARI A，et al．Probability-weighted hazard maps for comparing different flood risk management strategies:a case study［J］．Natural Hazards，2009，50(3):479-496．

［13］LAM D，LEONL，HAMILTON S，et al．Multi-model integration in decision support system:a technical user interface approach for watershed and lake management scenarios［J］．Environmental Modelling＆Software，2004，19(3):317-324．

［14］BÜTTNER O，SCHULZ M，MATTHIES M，et al．Flood and pollutant dispersal simulation in urban areas［C］∥Conference Proceedings of the International Conference“Science and Information Technologies for Sustainable Management of Aquatic Ecosystems”，2009:12-16．

［15］LEHFELDT R，MILBRADT P，PLÜSSA，et al．Propagation of a tsunami-wave in the North Sea［J］．Die Küste，2007，72:105-123．

［16］MALCHEREK A．Application of TELEMAC-2D in a narrow estuarine tributary［J］．Hydrological Processes，2000，14(13):2293-2300．

［17］VIONNET C A，TASSI P A，MARTIN VIDE JP．Estimates of flow resistance and eddy viscosity coefficients for 2 D modelling on vegetated floodplains［J］．Hydrological Processes，2004，18(15):2907-2926．

［18］GIARDINO A，LBRAHIM E，ADAM S，et al．Hydrodynamics and cohesive sediment transport in the Ijzer Estuary Blgium:Case Study［J］．Journal of Waterway，Port，Coastal and Ocean Engineering，2009，135(4):176-184．

［19］CHORDA J，MAUBOURGUET M M，ROUX H，et al．Two-dimensional free surface flow numerical model for vertical slot fishways［J］．Journal of Hydraulic Research，2010，48(2):141-151．

［20］JONES J E，DAVIES A M．An intercomparison between finite difference and finite element(TELEMAC)approaches to modelling west coast of Britain tides［J］．Ocean Dynamics，2005，55(3-4):178-198．

［21］ZHANG Cheng，GUILBAUD C．2D hydrodynamic modelling for Erhai Lake applying TELEMAC modelling system［EB/OL］．http:∥www．paper．edu．cn．2008．

［22］童朝锋，刘丰阳，邵宇阳，等．长江口北支崇启大桥处潮位和盐度过程研究［J］．水道港口，2012，33(4):291-298．(TONG Chao-feng，LIU Feng-yang，SHAO Yu-yang，et al．A modeling study on tidal and salinity process at Chongqi bridge cross section located in north branch of Yangtze Estuary［J］．Journal of Waterway and Harbor，2012，33(4):291-298．(in Chinese))

［23］HERVOUET JM．Hydrodynamics of free surface flows-modelling with the finite element method［M］．West Sussex:John Wiley＆Sons Ltd，2007．