基于系统可靠度的明钢管整体安全性研究

刘敬敏，杨绿峰，2，张 伟

(1．广西大学 土木建筑工程学院 工程防灾与结构安全教育部重点实验室，广西 南宁 530004;2．广西壮族自治区住房和城乡建设厅，广西 南宁 530028)

压力钢管是水电站输水系统的重要组成部分，其结构安全是水电站发电运营的基本保证．目前国内外压力钢管设计主要根据应力分类法进行［1－2］，也有研究者基于极限承载力进行管道整体安全研究［3－4］．实际工程结构中，钢材强度参数、静水压力、水锤和焊缝参数等具有显著的随机性，对压力钢管结构安全有重要影响．我国规范［1］已引入可靠度理论，根据与安全系数法保持等安全裕度的原则保证结构安全．同时国内外研究者考虑随机变量的统计特性，以控制部位或构件为研究对象，以应力为指标，建立了承载力极限状态功能函数，进行了压力钢管和压力容器的构件可靠度分析［5－7］．然而，管道结构是一个承载整体，不同部位常存在相同的随机变量，使各部位的构件可靠度间具有相关性，有必要从结构系统可靠度上把握结构整体安全性．

国内外学者对工程结构系统可靠度做了较多研究，提出了一些近似计算方法［8－10］，并已应用到重力式挡土墙［11］、平面钢闸门［12］和含腐蚀缺陷的工业管道［13］等结构中．然而，目前针对水电站明钢管系统可靠度的研究很少．鉴于此，本文考虑钢材强度、静水压力、水锤和焊缝系数的随机性，同时考虑明钢管跨中管壁、支承环近旁管壁边缘、加劲环及其近旁管壁、支承环及其近旁管壁4个基本部位之间的相关性，提出由这4个基本部位组成串联系统，采用JC法求解各基本部位的构件可靠度，进而利用二阶界限法求解水电站明钢管的系统可靠度，并用蒙特卡罗法验证本文方法的正确性，为明钢管结构整体安全评估提供参考．

1 随机变量与系统可靠度分析模型

1．1 随机变量及其概率分布

明钢管结构可靠度分析中，钢材强度、静水压力、水锤、焊缝系数、钢管自重和管内水重都具有随机性，同时鉴于钢管自重和管内水重的变异性较小［5］，本文考虑前4个参数作为管道系统可靠度分析的随机变量．统计研究表明，钢材屈服应力、水库最高水头Hmax与设计水头Hd的比值KWc、焊缝系数实测值φs与规范限定值φK的比值Khf服从正态分布［6－7］，其概率密度函数为:

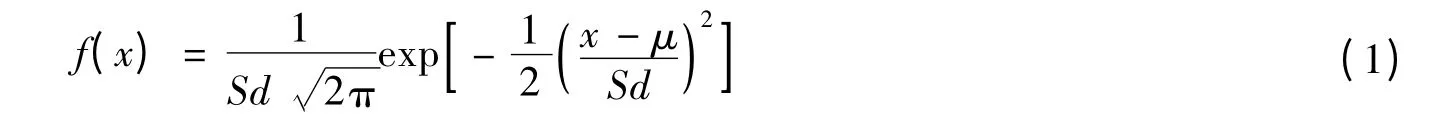
钢管中心水锤实测值Hs与计算值Hc的比值KWh服从极值Ⅰ型分布［5，7］，其概率密度函数为:

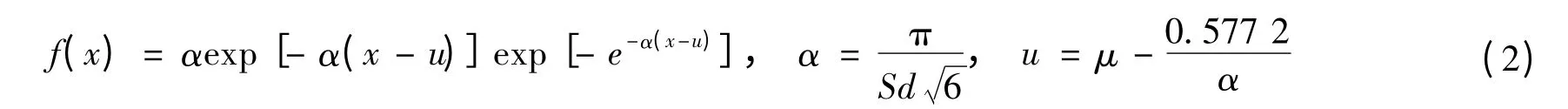
式中:μ和Sd分别为随机变量的均值和标准差，其统计特征值见表1［5－7］．

表1 随机变量统计特征值Tab．1 Statistical characteristic value of random variables

1．2 系统可靠度分析模型

水电站明钢管结构由跨中管壁、支承环近旁管壁边缘、加劲环及其近旁管壁、支承环及其近旁管壁4个基本部位组成，其中任何一个部位发生强度破坏都将导致明钢管结构失效，因而，明钢管系统可靠度分析模型即为由4个基本部位组成的串联系统，如图1．

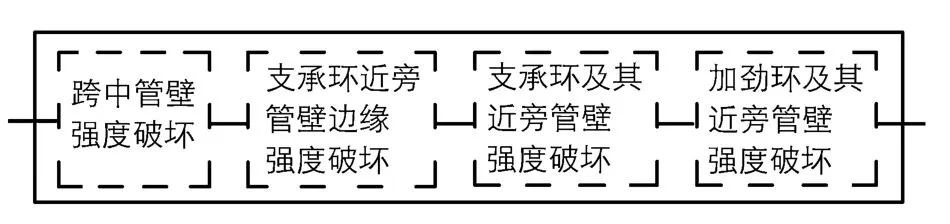
图1 明钢管系统失效的串联模型Fig．1 A series model for structural system failure of exposed penstock

2 明钢管结构系统可靠度分析

2．1 二阶界限法

若第i和第j个基本部位的功能函数间相关系数为ρij，则考虑任意两个部位同时失效的二阶联合失效概率Pfij的情况下，根据Ditlevsen提出的二阶界限公式［14］，可得明钢管结构系统失效概率Pfs的界限为:

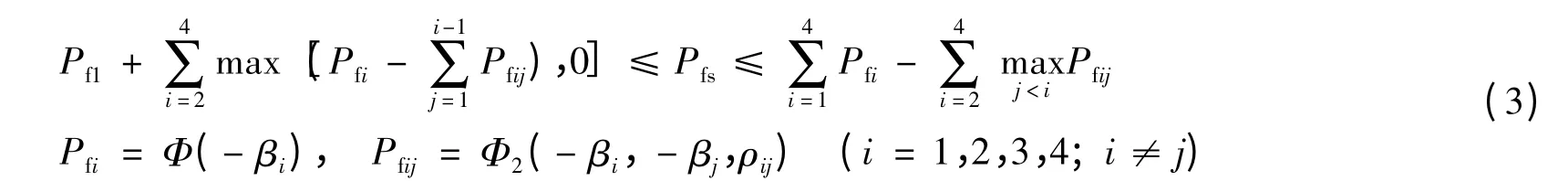
式中:Pfi和βi分别为第i个基本部位的失效概率和可靠指标;各基本部位的编号按失效概率的下降顺序排列，即使Pf1≥Pf2≥Pf3≥Pf4;Φ(－βi)为标准正态分布的累积分布函数值;Φ2(－βi，－βj，ρij)为二维标准正态分布的累积分布函数值:

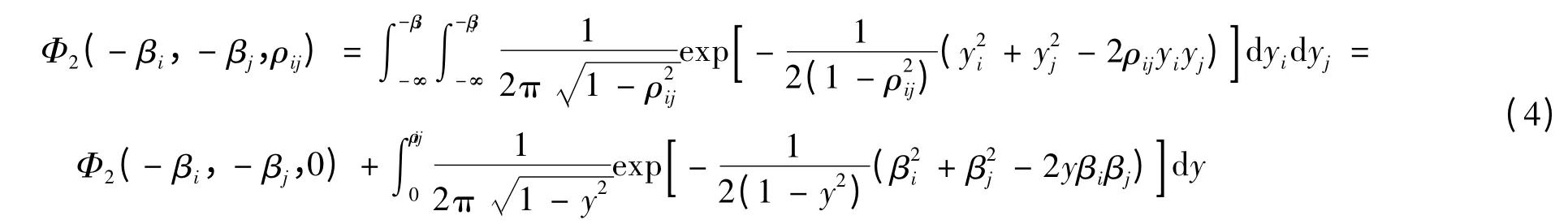
可见，通过式(3)求得明钢管强度安全系统失效概率的界限，进而可得系统可靠指标的界限，并可知系统可靠度的关键参数是各基本部位可靠指标βi和功能函数间的相关系数ρij．

2．2 各基本部位的功能函数及可靠指标

依据概率极限状态设计原则，采用Mises等效应力σe，且忽略对等效应力影响较小的σr，τxr和τrθ，则压力钢管强度的功能函数Z表达式为:

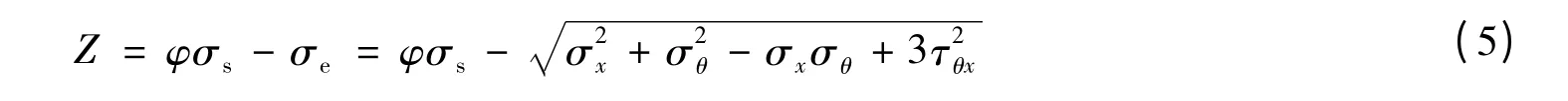
根据跨中管壁、支承环近旁管壁边缘、加劲环及其近旁管壁、支承环及其近旁管壁4个基本部位的受力特点，可由式(5)得到各基本部位功能函数表达式．

由于功能函数是非线性的，且水锤Hs为非正态随机变量，故引入JC法迭代求解各基本部位可靠指标．考虑随机变量(φ，σs，Hm，Hs)相互独立［15］，为便于表达，本文用xi(i=1，…，4)表示．将非正态随机变量进行当量正态化，获得当量正态随机变量x'i的标准差和均值:

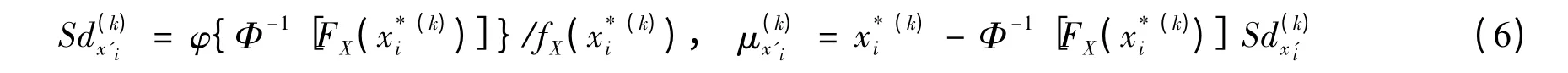
式中:FX(x)为边缘累积分布函数;Φ－1［·］为标准正态累积分布函数的反函数;k为迭代步数．

由正态随机变量的均值和标准差，可求得可靠指标和新的验算点:

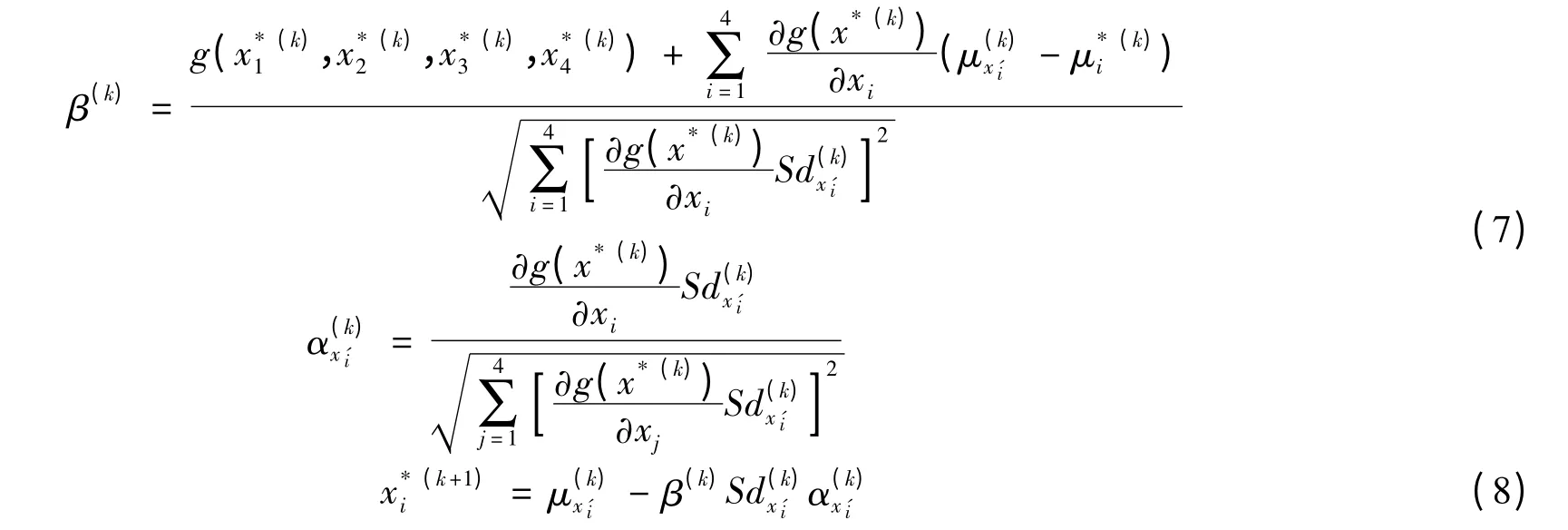
式中:αx'i表示第i个随机变量对整个功能函数值的标准差的影响，称为灵敏系数，即为结构可靠度对该随机变量的敏感系数．

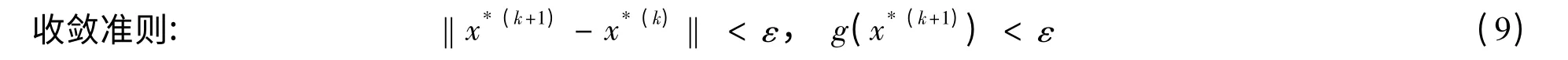
式中:ε为收敛容差，取0．01．

2．3 各基本部位功能函数间的相关系数［16］

将明钢管4个基本部位的功能函数分别在各自的验算点处通过一阶泰勒级数展开为线性函数，则任意两个线性功能函数ZLi和ZLj之间的相关系数为:

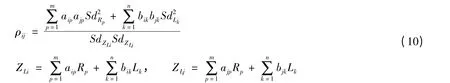
式中:a和b分别为抗力R和荷载效应L的系数;m和n分别为R和L中随机变量个数．

3 明钢管结构系统可靠度分析步骤

明钢管结构系统可靠度分析步骤分以下7步:

(1)确定水电站明钢管计算管段中各基本部位的随机变量统计信息，并设定第i个基本部位的随机变量验算点初值通常取为均值;

(2)按式(6)求得Hs当量正态化后的均值和标准差，并由式(7)和(8)求得可靠指标β(0)和新验算点

(3)将验算点代入式(9)，若满足，则停止迭代，得第i个基本部位的可靠指标βi=β(0);否则，令(φ*(0)，，转步骤(2)继续迭代，直至满足式(9)，得βi=β(k);

(4)重复前3步，求得4个基本部位的可靠指标、验算点坐标及失效概率;

(5)将各功能函数在验算点处进行线性化，由式(10)确定相关系数;

(6)按式(4)计算二阶联合失效概率;

(7)按式(3)估计明钢管结构系统失效概率的上下界限，进而得到系统可靠指标界限，为明钢管整体安全性评估提供依据．

4 工程实例分析

4．1 平直管道

图2所示水平布置的明钢管，依据规范设计管壁厚t0=18 mm;水库设计水位Hd0=134．0 m，水锤为30%静水压;加劲环厚度a1=18 mm，高度h1=220 mm;支承环厚度a2=18 mm，高度h2=260 mm;采用16 Mn钢，钢材重度γs=78．5 kN/m3，弹性模量E=2．06×105MPa．以跨中管壁、支承环近旁管壁边缘、加劲环及其近旁管壁、支承环及其近旁管壁的最危险点为计算点．

取表1的钢材强度统计值，并按规范［1］取单面焊接的焊缝系数φK，可得实际焊缝系数φs、管道中心轴处的静水头Hm及水锤Hs的均值分别为0．90，123．28和39．40 m，变异系数分别为0．050，0．124和0．239．首先采用上一节建立的方法计算明钢管的系统可靠度，同时采用蒙特卡罗法对计算结果进行校验．蒙特卡罗法是抽样统计方法，它通过对基本随机变量大样本抽样，并将各组样本确定的结构抗力和响应量逐一代入功能函数表达式确定结构的失效概率．理论上，只要样本数量足够大，蒙特卡罗法就可取得足够精确的计算结果，因而通常用于检验其他随机方法的正确性及计算精度．但大样本抽样也导致蒙特卡罗法计算效率较低，所以较少直接用于工程实际．从图3可见，当抽样次数达到3 000万次时，蒙特卡罗法计算结果趋于稳定，如图3所示．本文方法和蒙特卡罗法计算结果见表2．

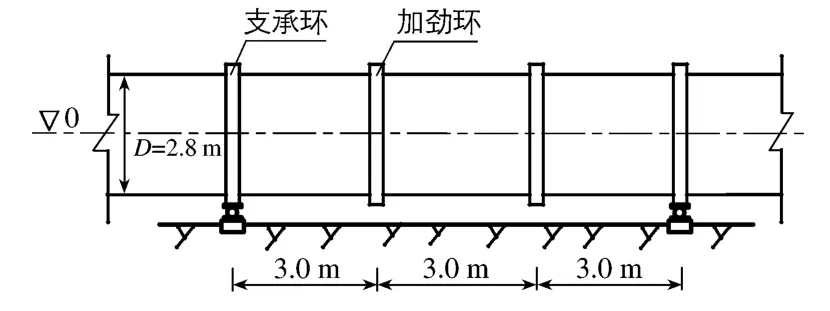
图2 计算简图 Fig．2 Calculation diagram

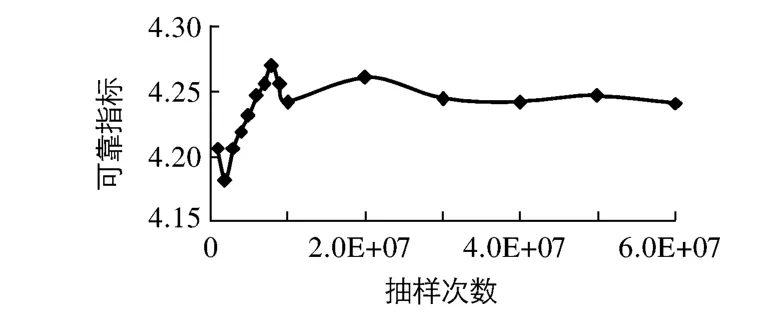
图3 蒙特卡罗法计算结果收敛趋势Fig．3 Convergence figure given by Monte Carlo method

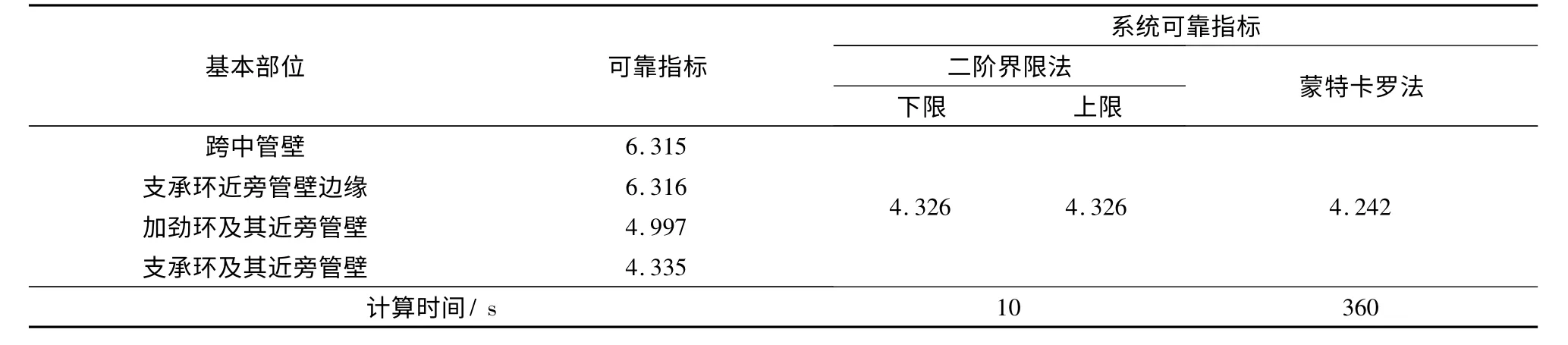
表2 基本部位可靠指标和系统可靠指标Tab．2 Reliability index of primary parts and structural system reliability index

从表2可以看出，二阶界限法计算的上下限值非常接近，且与蒙特卡罗法结果的相对差约为2．0%，表明计算结果有良好的精度．同时，由图3可知，蒙特卡罗法需要抽样3 000万次左右才能使结果趋于稳定，需耗时360 s;二阶界限法仅耗时10 s，有良好的计算效率．4个基本部位中，跨中管壁和支承环近旁管壁的可靠指标很高，而支承环及其近旁管壁的可靠指标很低，且系统可靠指标与支承环及其近旁管壁的非常接近，说明支承环及其近旁管壁部位是明钢管系统失效的控制部位．

4．2 倾斜管道

图4所示某水电站倾斜管道，最大流量为30．24 m3/s，伸缩节用金属丝油浸石棉、石墨盘根，盘根填料长度b=0．3 m，填料与管壁间摩擦系数fk=0．3，伸缩节内径D1=2．824 m;采用摇摆式支座，支座与管壁间摩擦系数为f=0．1．水库设计水位Hd0=215．5 m，水锤为30%静水压．依据规范设计管壁厚t0=12 mm;加劲环厚度a1=12 mm，高度h1=180 mm;支承环厚度a2=12 mm，高度h2=200 mm;采用16 Mn钢，E=2．06×105MPa，重度γs=78．5 kN/m3．

管道跨中、支承环近旁、加劲环和支承环的中心轴处静水头变异系数为0．124，均值分别为72．26，70．77，71．79和70．77 m;水锤变异系数为0．239，均值分别为23．09，22．62，22．94和22．62 m;焊缝系数和钢材屈服应力特征值同算例1．采用本文方法求系统可靠度，并利用蒙特卡罗法进行检验，蒙特卡罗法抽样500万次以上计算结果基本稳定，如图5所示．两种方法的计算结果见表3．

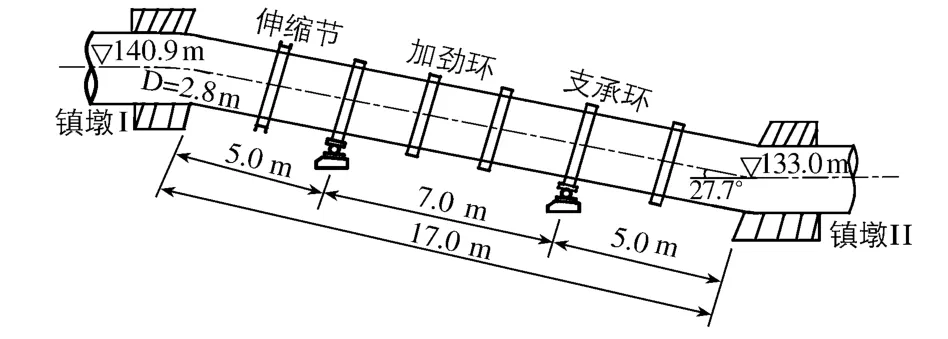
图4 计算简图 Fig．4 Calculation diagram

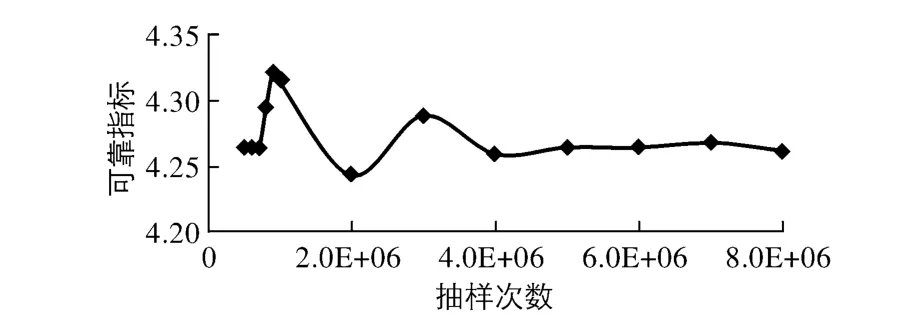
图5 蒙特卡罗法计算结果收敛趋势Fig．5 Convergence figure given by Monte Carlo method

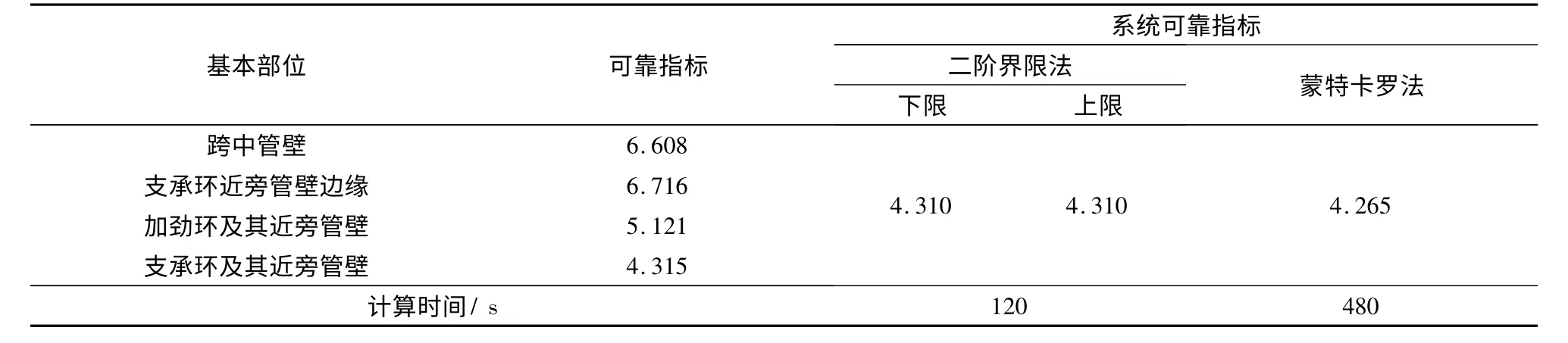
表3 基本部位可靠指标和系统可靠指标Tab．3 Reliability index of primary parts and structural system reliability index

根据表3和图5可知，对于有轴向力作用的倾斜管道，二阶界限法与蒙特卡罗结果的相对差约为1．1%，也具有良好的计算精度，说明该方法能应用于水电站明钢管系统可靠度中;二阶界限法计算效率高于蒙特卡罗法;跨中管壁和支承环近旁管壁边缘的可靠指标较高，支承环及其近旁管壁部位的可靠指标相对较低，是明钢管系统失效的控制部位．

5 随机变量影响分析

5．1 可靠指标对随机变量的敏感性分析

由式(7)可得各基本部位可靠度对随机变量的敏感系数，2个算例的计算结果见表4．由表4可知，不论是平直管道还是倾斜管道，钢材的屈服强度σs和水锤Hs的敏感系数较大，而静水压力Hm和焊缝系数φ相对较小，说明基本部位可靠指标受钢材强度和水锤影响相对较大．

表4 各基本部位可靠度对随机变量的敏感系数Tab．4 Sensitivity coefficient of primary parts reliability against random variables

5．2 随机变量均值对系统可靠度的影响

钢材强度、静水压力、水锤和焊缝系数的取值对明钢管可靠度有不同影响，保持这些随机变量的变异系数不变，使其均值在区间［μ－Sd，μ+Sd］内变化，均值对明钢管系统可靠度的影响规律如图6．其中，平直管道中4个随机变量的设计值分别为342．56 MPa，134．00 m，40．20 m和0．90;倾斜管道中的设计值分别为342．56 MPa，78．55 m，23．56 m和0．90．

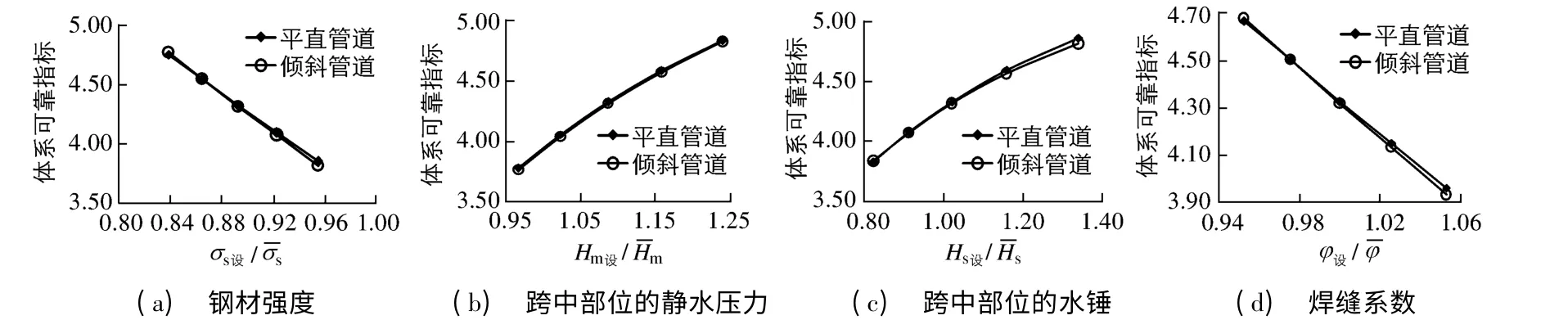
图6 随机变量均值对系统可靠度的影响Fig．6 Influence of the mean values of random variables on system reliability

由图6可知，明钢管系统可靠度随着钢材强度和焊缝系数均值的减小而线性减小，随着静水压力和水锤均值的减小而呈近似线性增大．就本文算例来看，当钢材强度的设计值与均值之比以及焊缝系数的设计值与均值之比分别小于0．9和1．02，静水压力和水锤的设计值与均值之比分别大于1．07和1．00时，能使明钢管系统可靠指标大于规范目标值4．2，能较好地保证结构整体安全性．

6 结语

文中提出了由水电站明钢管的跨中管壁、支承环近旁管壁边缘、加劲环及其近旁管壁、支承环及其近旁管壁4个基本部位组成的串联系统模型，给出了明钢管结构系统可靠度的计算方法与步骤，结合典型明钢管工程实例分析了系统可靠度及随机变量的影响．研究表明:支承环及其近旁管壁由于存在较大局部应力，使得该部位的可靠度水平相对较低，是明钢管系统失效的控制部位，为保证结构整体安全要求，设计中应重视提高该部位的可靠性，必要时可采取局部工程措施以提高结构系统可靠度;钢材强度和水锤对明钢管各部位可靠度的影响较大，而静水压力和焊缝系数的影响相对较小;随机变量均值对明钢管系统可靠度的影响明显，需在设计、施工和运行各环节中严格控制均值波动范围，提高结构的整体安全性．

［1］DL/T 5141－2001，水电站压力钢管设计规范［S］．(DL/T 5141－2001，Specification for design of steel penstocks of hydroelectric stations［S］．(in Chinese))

［2］ASME BPVC 2010，Rules for Construction of Pressure Vessels［S］．

［3］张伟，杨绿峰，韩晓凤．基于弹性补偿有限元法的无梁岔管安全评价［J］．水利学报，2009，40(10):1175-1183．(ZHANGWei，YANG Lv-feng，HAN Xiao-feng．Safety evaluation of shell type bifurcated pipes using elastic compensation finite element method［J］．Journal of Hydraulic Engineering，2009，40(10):1175-1183．(in Chinese))

［4］YANG Lv-feng，ZHANG Wei，YU Bo，et al．Safety evaluation of branch pipe in hydropower station using elastic modulus reduction method［J］．Journal of Pressure Vessel Technology，2012，134(6):1-7．

［5］安旭文，侯建国，何英明，等．水电站压力钢管明管的可靠度校准分析［J］．武汉大学学报:工学版，2003，36(6):31-35．(AN Xu-wen，HOU Jian-guo，HE Yin-ming，et al．Reliability calibration analysis of exposed penstocks for hydropower stations［J］．Engineering Journal of Wuhan University，2003，36(6):31-35．(in Chinese))

［6］张雪颖，索丽生．压力钢管可靠度分析方法探讨［J］．水利水电科技进展，2002，22(2):22-24．(ZHANGXue-ying，SUO Li-sheng．Reliability analysis for penstocks［J］．Advances in Science and Technology of Water Resources，2002，22(2):22-24．(in Chinese))

［7］何英明，侯建国，安旭文，等．地下埋管可靠度校准分析［J］．武汉水利电力大学学报，1995，32(5):64-68．(HE Yingming，HOU Jian-guo，AN Xu-wen，et al．Reliability analysis of underground penstock［J］．Journal of Wuhan University of Hydraulic and Electric Engineering，1995，32(5):64-68．(in Chinese))

［8］张小庆，康海贵，王复明．一种新的体系可靠度的近似计算方法［J］．工程力学，2004，21(1):93-97．(ZHANG Xiaoqing，KANG Hai-gui，WANG Fu-ming．A new approximate algorithm for calculation of the failure probability of a system［J］．Engineering Mechanics，2004，21(1):93-97．(in Chinese))

［9］ZHAO Y G，ZHONG W Q，ANG A H S．Estimating joint failure probability of series structural systems［J］．Journal of Engineering Mechanics，2007，133(5):588-596．

［10］YANG L F，YU B，JU J W．System reliability analysis of spatial variance frames based on random field and stochastic elastic modulus reduction method［J］．Acta Mechanica，2012，223(1):109-124．

［11］杜永峰，余钰，李慧．重力式挡土墙稳定性的结构体系可靠度分析［J］．岩土工程学报，2008，30(3):349-353．(DU Yong-feng，YU Yu，LI Hui．Analysis of reliability of structural systems for stability of gravity retaining walls［J］．Chinese Journal of Geotechnical Engineering，2008，30(3):349-353．(in Chinese))

［12］李典庆，吴帅兵．水工平面钢闸门主梁多失效模式相关的系统可靠度分析［J］．水利学报，2009，40(7):870-877．(LI Dian-qin，WU Shuai-bing．System reliability analysis on main girder of plane gates considering multiple correlated failure modes［J］．Journal of Hydraulic Engineering，2009，40(7):870-877．(in Chinese))

［13］ZHOU W．System reliability of corroding pipelines［J］．International Journal of Pressure Vessels and Piping，2010，87(10):587-595．

［14］DITLEVSEN O．Narrow reliability bounds for structural system［J］．Journal of Mechanics，1979，7(4):483-472．

［15］张雪颖，索丽生，胡爱宇，等．压力钢管荷载中静水压力与水击压力的相关性研究［J］．水电站设计，2003，19(3):18-19．(ZHANG Xue-ying，SUO Li-sheng，HU Ai-yu，et al．Analysis of correlation of hydrostatic pressure and water hammer pressure in the penstock［J］．Design of Hydroelectric Power Station，2003，19(3):18-19．(in Chinese))

［16］李清富，高健磊．工程结构可靠性原理［M］．郑州:黄河水利出版社，1999:103-104．(LI Qing-fu，GAO Jian-lei．Reliability theory of engineering structures［M］．Zhengzhou:Yellow River Water Conservancy Press，1999:103-104．(in Chinese))