钢弹簧浮置板轨道结构谐响应分析＊

蒋崇达 雷晓燕

（华东交通大学铁路环境振动与噪声教育部工程研究中心，330013，南昌∥第一作者，硕士）

钢弹簧浮置板轨道作为一种新型有效的减振降噪轨道结构，凭其较低的系统固有频率，可以有效地过滤或衰减掉高频的外界激振并拥有较低的养护维修成本，已经在世界范围内得到广泛应用。

国内学者对这种轨道结构的隔振性能进行了大量研究。针对不同浮置板板长的计算模型，文献［1］以欧拉梁模型模拟钢轨，以连续分布质量层模拟短型浮置板；文献［2］将钢轨与浮置板分别用欧拉梁来模拟中长型浮置板；文献［3］考虑了板间的不连续性，不同板长的浮置板采用多梁模型来模拟；文献［4］将浮置板简化为自由边界的基尔霍夫薄板，建立了二维浮置板轨道。上述模型中，连续分布模型反映不出有限长浮置板自身模态对高频段隔振性能的影响，计算结果反映的是高频段平均隔振性能［5］。应该考虑浮置板间的不连续性，但又不能将板间完全断开。事实上，钢弹簧浮置板之间是通过上置式剪力铰连接，能较好地保证轨道的连续性。剪力铰的作用必然将影响系统的弯曲振动模态，同时弯曲振动模态对浮置板轨道的隔振性能又有显著影响［6］。因此，本文考虑浮置板之间的不连续性，并将剪力铰视为刚体；通过耦合相邻板间剪力铰栓接处的竖向自由度来模拟剪力铰的约束。基于ANSYS软件建立了浮置板有限元模型，对比了不同板长下的钢弹簧浮置板轨道的振动模态；并通过谐响应分析对比不同系统参数下的轨道结构形式对地基反力的影响。

1 计算模型及参数

1.1 钢弹簧浮置板轨道计算模型及参数

模型在建立过程中选用的单元类型［7］及模型的边界条件要依据实际中的具体情况而定。参考北京地铁实际铺设的浮置板整体道床，轨道长度取60m。钢轨类型为CHN60，钢轨采用Beam188梁单元进行网格划分，将扣件处钢轨节点的横向自由度、纵向自由度和对应浮置板节点耦合，用来模拟扣件的约束作用；扣件采用Combin14弹簧阻尼单元进行网格划分，刚度为50kN／mm，阻尼为5×104N·s／m；浮置板采用Solid45实体单元进行网格划分，将浮置板截面等效为面积相等的矩阵截面，5种板长对应参数见表1，相邻浮置板是通过剪力铰相连，因此将相邻板端节点的竖向自由度耦合，用来模拟剪力铰。钢弹簧支座只考虑竖向振动，采用Combin14弹簧阻尼单元进行网格划分，刚度为6.9 kN／mm，阻尼为7.5×104N·s／m，基础节点全部约束。谐响应分析时，根据地铁B型车 （轴距2.2 m、定距12.6m）确定轴重及轴载位置，取一节车加载；在相应轮载处各加幅值为78.4kN（1／2轴重）、频率为0～100Hz的简谐力。由此，钢弹簧浮置板轨道有限元模型如图1所示。

表1 钢弹簧浮置板尺寸及板长工况

图1 钢弹簧浮置板轨道计算模型（板长＝3.7m）

1.2 不设浮置板的轨道计算模型及参数

为对比钢弹簧浮置板的隔振效果，假设另外一种轨道形式：钢轨直接通过扣件固定在隧道基础上，且取一半轨道研究；钢轨和扣件所采用的单元和参数如上；将相应的力（如上）加载在单边轨上。

2 模态分析

本文使用ANSYS有限元软件对上述钢弹簧浮置板有限元模型进行模态分析，得到结构的固有频率和振型。文献［6］等通过改变系统参数对浮置板轨道进行了模态分析，但对板长的分析较少且多针对单块板。因此，本文仅对板长这个参数进行模态分析，其它参数不再赘述。

2.1 固有频率

通过模态分析可以得到钢弹簧浮置板结构的固有频率，5种工况取其前10阶的结果，如图2所示，更高阶部分省略。

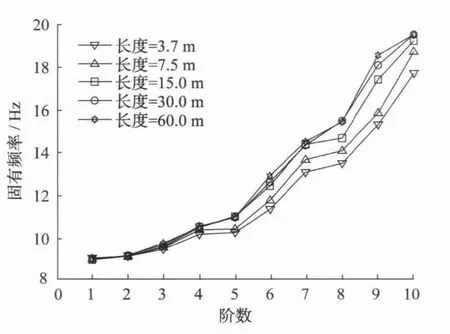
图2 浮置板长度对固有频率的影响

由图2可知：板长对系统基频的影响不大，都在9Hz左右。针对前10阶模态：板长最短的3.7m浮置板各阶固有频率最小，当板长大于30m后，系统固有频率变化规律趋于相同。

2.2 振型

限于篇幅，仅给出工况1和工况5的前6阶振型（见图3、图4）。

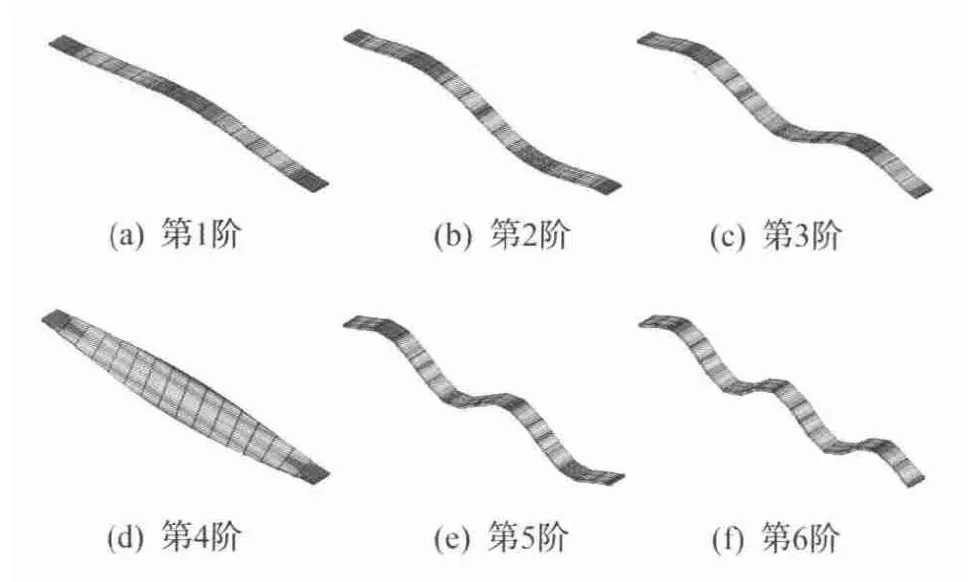
图3 工况1的前6阶振型

图4 工况5的前6阶振型

由图3、4可知：不同板长的浮置板表现出了不同的振型。板长越长，系统的振型受单块浮置板的转动和扭转振型影响越大，从而影响轨道线路的整体振型。板长越短越难激发其单块浮置板的弯曲和扭转的振型，多以前后点头和左右转动组合成系统的各阶振型，因而在整体变形上沿线路方向不是连续的，且板长越短不连续性越大，导致剪力铰处的钢轨将承受更大的变形。随着板长的减小，这种薄弱环节将更多。因此，从振型的角度看应尽量选用较长的浮置板轨道。

3 谐响应分析

浮置板轨道结构在不同外界激振频率下的力学传递性是评价其隔振性能的重要依据，用隔振效率作为指标来评价浮置板轨道结构的隔振性能［6］。隔振计算公式如式（1）。

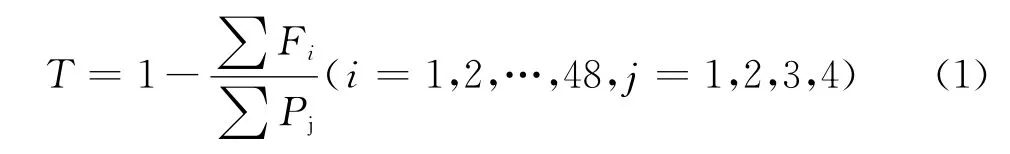
式中：

Fi——沿线路方向各钢弹簧支座反力的力值（共48个弹簧支座）；

Pj——单个车轮施加的荷载（共有4个车轮）。

3.1 减振效果

为了对比钢弹簧浮置板的隔振效果，分别对上述钢弹簧浮置板轨道模型（取板长3.7m）和不设置浮置板的轨道模型进行谐响应分析，得出两种轨道基础反力随激振频率分布图，见图5。

图5 减振效果对比图

由图5可知：通过扣件直接固定在隧道基础上，基础反力主要集中在激振力作用点的范围内；基础反力随频率的变化不大且保持较大的幅值。可知，不设置减振轨道时，所有频率内都将产生较大的基础反力。

当设置钢弹簧浮置板后，基础反力在基频处最大，并在线路中心处得到了叠加，这是因为剪力铰能使轨道板间的竖向力得到传递。随着频率的增大，基础反力迅速衰减，轨道全局性弯曲振动起来。分别于20.03Hz、28.23Hz、37.44Hz、53.35Hz处发生共振，其对应于系统的第9、12、15、22阶固有频率。这些共振频率对应的振型多以波浪型弯曲振动为主。

对比图5中两种结果可见：钢弹簧浮置板可以很好地将轮载的能量沿线路分散开，增大了列车振动的纵向影响范围。只有在9Hz左右时，钢弹簧浮置板最大共振处的基础反力和不设置浮置板时几乎相等，没有减振效果。但对于大于9Hz的频段，幅值迅速下降。从空间位置上力的幅值来看，钢弹簧浮置板的减振效果显著。

3.2 板长影响

对5种板长进行谐响应分析，利用式（1），可得轨道系统总体的隔振率（见图6）。不同工况下的基础反力随激振频率分布图见图7。

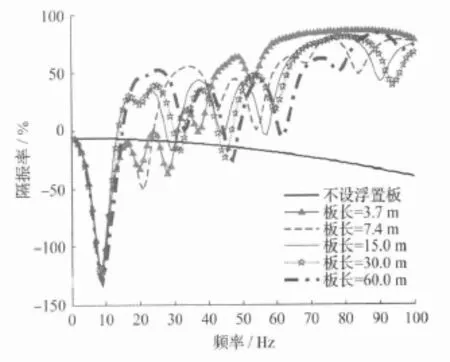
图6 不同工况下的总体隔振率

由图6及图7可知：不同板长由于不同的振型导致其隔振效率随频率变化并不一致。基频处，不同板长的地基反力总和几乎相同，但长型浮置板的影响范围更广。各板长的高阶共振尖峰表现的是轨道系统的弯曲振型，在分布图上表现为基础反力随线路方向明暗交替变化。频率在15～30Hz内，短型浮置板总体隔振效果不是很好，频率大于60Hz时短型浮置板的隔振效果好于长型浮置板。长型浮置板轨到在中低频段（＜20Hz）部分，由于其频率低，波长相对较长，更难被消除。而中高频部分经过隧道衬砌、大地的传播后，到达地表时很大程度上得到了衰减。从这个角度看，长型浮置板具有较好的低频隔振效果。

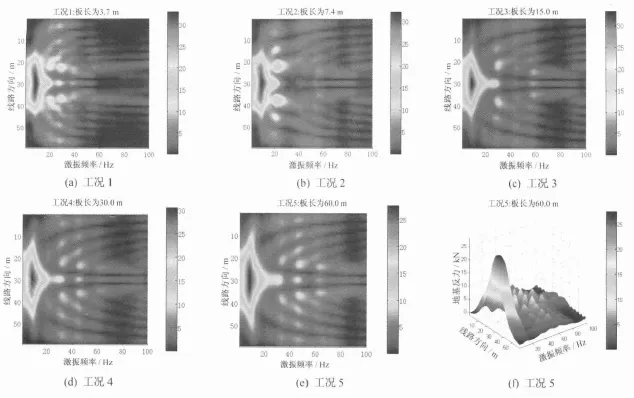
图7 不同板长下基础反力随激振频率分布图

3.3 板厚的影响

由单自由度隔振原理可知，系统的参振质量是一项重要参数，本文通过板厚的角度来研究参振质量的影响。可得5种板厚（0.3、0.4、0.5、0.6、0.7m）的基础反力分布图及总体隔振率，见图8及图9。

图8 不同板厚下基础反力随激振频率分布图

由图9可知，板厚对系统的基频略有影响：板越厚系统基频越小且基频处的共振幅度越大。因为增加板厚的同时增加了系统的参振质量，系统固有频率降低。对于10～40Hz这个频段，板越厚系统隔振效果越好。由图8可知，尽管在基频处板厚0.7 m较板厚0.3m的隔振率相差50%且影响范围相差10m，但地基节点处的最大反力却几乎相等。同时，板越厚基频左右处的最不利频段越窄。综上所述，板厚越大，系统隔振效果越好；工程中应结合隧道内的净空要求取得最合适板厚。

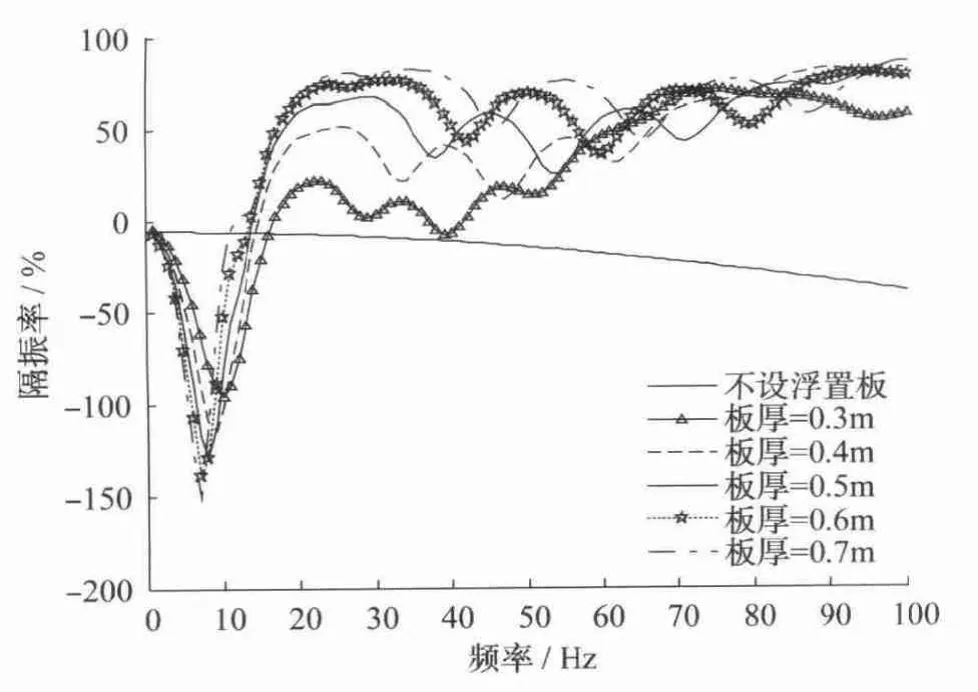
图9 不同板厚下的总体隔振率

3.4 支座刚度的影响

由两自由度隔振模型结果可知：当两个弹簧刚度相差较大时，系统隔振效果主要受较小刚度弹簧的影响；实际中扣件刚度比支座刚度大很多，对系统的隔振效果影响可以忽略不计。本文仅针对钢弹簧支座的刚度（5×106N／m，10×106N／m，20×106N／m，40×106N／m，80×106N／m）进行分析，可得5种工况下的基础反力分布图及总体隔振率，见图10及图11。

由图10及图11可知，钢弹簧垂向刚度系数对于系统的隔振性能具有重要的影响：支座刚度越大系统基频越大且基频处的共振幅度越大，其中工况15较工况11基频处的隔振率相差高达300%。因为支座刚度较小的浮置板结构能够产生较大的垂向变形，在外力由浮置板传递至基础的工程中，能更好地将外界激振产生的能量转移到浮置板上并将其有效地衰减。对于高频段，支座刚度越大隔振效果越差。地基节点处的最大支反力也随着支座刚度的增加而增加，其中工况15较工况11基频处的最大支反力放大了近3倍。可见降低支座刚度可以有效地提高系统的隔振效果。

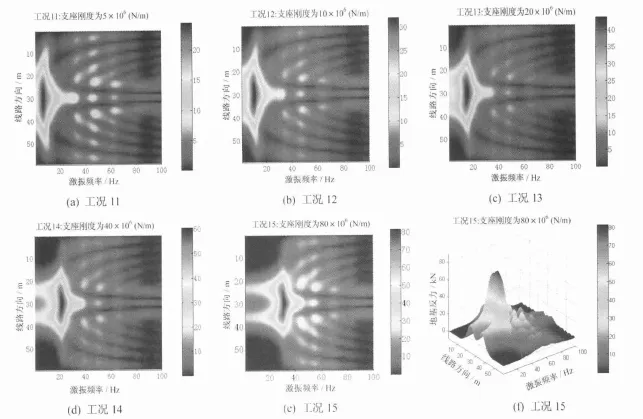
图10 不同支座刚度下基础反力随激振频率分布图

3.5 支座阻尼的影响

阻尼是耗散外界能量的一种方式，尤其对系统在动力作用下共振峰处的振动响应有着重要的影响。针对支座阻尼（2.5×104N·s／m，5×104N·s／m，10×104N·s／m，20×104N·s／m，40×104N·s／m）参数，可得5种工况下的基础反力分布图及总体隔振率，见图12及图13。

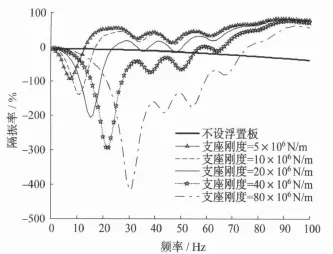
图11 不同支座刚度下的总体隔振率

由图12及图13可见，钢弹簧阻尼的变化对系统固有频率的大小没有影响，但对所研究的频段内隔振效率有着较大的影响。对于基频处，工况16较工况20基频处总体隔振率相差高达350%。然而对于中高频段，过大的支座阻尼并不利于系统的隔振。由图12可见，对于低阻尼（工况16）基频处在较大范围（两节车长）内保持着较大的基础反力，多节车辆运行时将导致相邻基础反力的叠加不利于隔振；对于大阻尼（工况17），基频处地基反力主要集中在加载范围内（一节车），对于中高频地基反力主要集中在转向架下，隔振效果甚至不如基频处。综上所述，增加钢弹簧阻尼可以有效地降低浮置板轨道低阶共振频率处系统响应；对于中高频却有着相反的效果，不利于力的衰减。

图12 不同支座阻尼下基础反力随激振频率分布图

4 结语

本文利用ANSYS建立了钢弹簧浮置板三维有限元模型，探讨了不同参数下结构的隔振效果。通过振型分析和谐响应分析得到如下结论：

（1）一阶固有频率直接影响钢弹簧浮置板在低频范围内的隔振性能。为了提高隔振效果，应尽可能降低钢弹簧浮置板的一阶固有频率，可通过增加浮置板的质量和降低钢弹簧的刚度来实现，但过大的质量将增大轨道结构高度，过低的弹簧刚度又将使轨道结构不稳定，导致钢轨磨耗增加，因此应合理选择浮置板质量和钢弹簧刚度。

（2）长型浮置板轨道由于连续变化的振型可以更好地保护钢轨，长型浮置板的隔振效果优于短型浮置板，尤其是在低频范围；长型钢弹簧浮置板轨道相对于短型浮置板轨道更容易施工，工程造价也较低。目前长型钢弹簧浮置板轨道多采用现场整体浇注，施工简单，质量可靠。

（3）增加钢弹簧阻尼可以有效地降低浮置板轨道低阶共振频率处系统响应；对于中高频却有着相反的效果，不利于力的衰减。

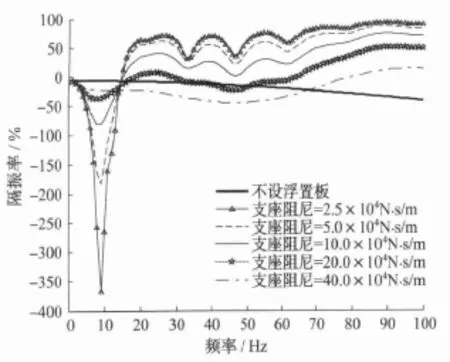
图13 不同支座阻尼下的总体隔振率

［1］吴川，刘学文，黄醒春.短型浮置板轨道系统隔振性能研究［J］.振动与冲击，2008，27（8）：74.

［2］刘学文，吴川.长型浮置板轨道隔振系统理论分析－传递率［J］.计算力学学报，2009，26（6）：924.

［3］李增光，吴天行.浮置板轨道参数激励振动研究［J］.振动与冲击，2010，29（2）：17.

［4］李增光，吴天行.浮置板轨道二维建模及隔振性能分析［J］.铁道学报，2011，33（8）：93.

［5］李增光，吴天行.浮置板轨道动柔度计算方法与隔振性能研究［J］.振动工程学报，2007，20（3）：207.

［6］丁德云，刘维宁，张宝才.浮置板轨道的模态分析［J］.铁道学报，2008，30（3）：61.

［7］王新敏.ANSYS工程结构数值分析［M］.北京：人民交通出版社，2007.

［8］姚纯洁，郑玄东，肖安鑫.钢弹簧浮置换轨道结构静力学分析［J］.城市轨道交通研究，2012（2）：104.