基于二维局域波和角点匹配的多模态图像配准
王小平,静大海
(河海大学 计算机与信息学院,江苏 南京 211110)
图像配准目前一直是图像处理和计算机视觉领域中的一个基本问题,如何度量两幅图像是否真正配准是图像配准的一个核心问题,直接决定了是否可以进行全自动配准。
由于图像是来自多种成像设备,所以多模态图像的结构信息比单模态图像更加丰富和全面[1]。但是在各种因素的影响下,使得精确配准多模态图像变得十分困难。近年来,一些学者利用互信息方法把小波分解后剩余图像进行配准,得到了较好的效果[2-4]。局域波分解是基于信号局部特征的分解,与小波分解相比局域波分解有更优的分解能力。另外角点是图像中像素灰度值在各个方向变化非常高的点[5],它是描述图像的一个重要点特征。因此角点检测是多模态图像配准的优越算法,本文利用局域波分解后的剩余图像,并以角点检测作为图像配准的测度,提出一种基于剩余图像和角点检测的自动点匹配的多模态图像配准方法。以下将首先要描述角点检测理论,二维局域波分解方法,然后将二者结合起来产生多模态图像配准的新方法。
1 多模态图像配准方法
1.1 基于角点检测的自动点配准方法
图像进行角点匹配首先要利用Harris算子进行检测。Harris[5]算子是Harris C和Stephens M J提出的一种基于信号的点特征提取算子,是一种有效的点特征提取算子,在图像处理中它对图像旋转、灰度变化、噪声影响和视点变换不敏感,因此它也是比较稳定的一种点特征提取算子。
利用Harris算子对两幅图像进行检测,检测结果为2个角点集合,这两个集合角点之间是多对多匹配的。这是一个初始匹配点集。利用互相关的方法来度量图像A中角点p和图像B中角点q的相似程度,其表达式为:
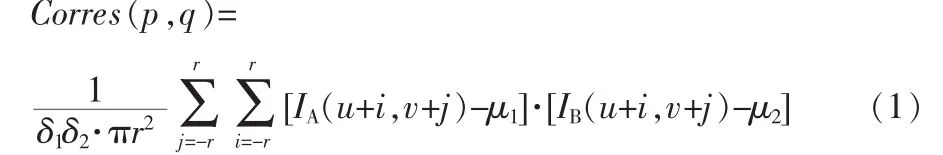
式中,μ1(μ2)是图像 A(B)在点 p(q)附近的局部均值;δ1(δ2)是图像 A(B)在点 p(q)附近的方差,r为角点邻域半径。IA与IB分别为图像A与B的亮度函数。
为保证计算精确度的同时提高搜索速度,图像A中的角点p取以p为中心,以为半径的圆域为邻域。在图像B中找到一矩形搜索区域,该搜索区域的中心与A中p点具有相同坐标值。尺寸为2du×2dv。如图1所示。利用式(5)计算矩形搜索区中每一角点q与图像A中角点p的相似度。
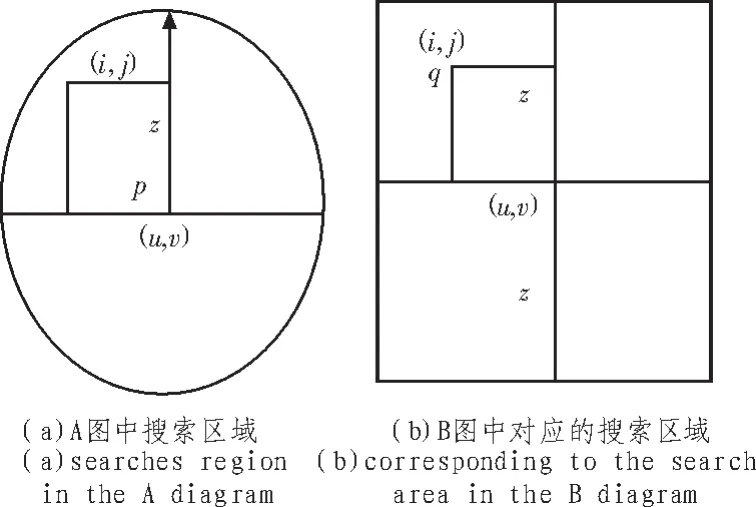
图1 互相关匹配中两图搜索区域Fig.1 Searching area of two pictures in cross-correlation
1.2 二维局域波分解
局域波分解[6]是把信号进行平稳化处理,产生了一系列具有不同特征尺度的数据序列——内禀模式函数(Intrinsic Mode Function,IMF)和一个剩余量,目前一维局域波分解方法包含了小波变换的多分辨率的优势,同时又克服了小波变换需要选取小波基的困难,从信号本身的尺度特征出发对信号进行分解。鉴于一维局域波分解的成功应用,文中将它推广到二维,提出了二维局域波分解并把它用于图像处理中。
假设待处理的图像为 F(x,y),对其进行局域波分解,首先利用形态学的方法对图像进行滤波重建[7],用连通结构元对图像进行腐蚀,对那些没有被完全腐蚀掉的部分进行重建恢复,对图像进行求极值处理,然后将图像两个极值利用径向基函数进行插值,生成极大包络曲面和极小包络曲面,对极大包络曲面和极小包络曲面求代数均值m(x,y),从图像中减去极大极小包络的代数均值,得到它们的差值,即:
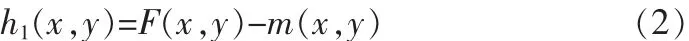
但由于包络均值这样的近似,这一过程可被重复多次,第二次筛选是需要以h1(x,y)作为待处理数据:
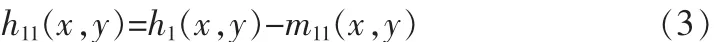
当进行到第 k 次,于是:h1(k-1)(x,y)-m1k(x,y)=h1k(x,y)=D1(x,y)。
式中D1(x,y)就是从原始信号中获得的第一个局域波分量。如果 2 个连续分解向量 h1k(x,y)与 h1(k-1)(x,y)之差小于一定阈值则可停止分解:
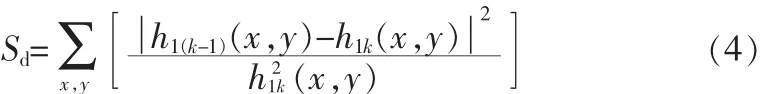
总的来说,D1(x,y)中应包含原始信号中最短的周期分量,即信号尺度最小的部分。把从原始图像信号F(x,y)中分离出的信号R1(x,y)作为新数据进行处理,其中:
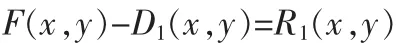
显然,R1(x,y)中包含信号中较大尺度的部分,依次继续筛选下去
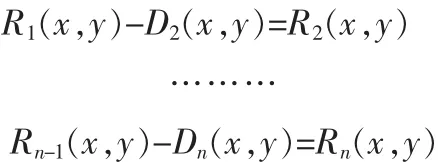
这时就有
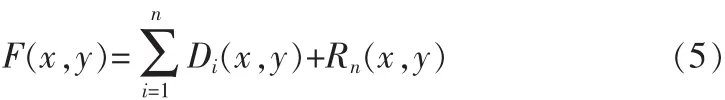
式中:Di(x,y)是第 i个 IMF(细节图像),Rn(x,y)是 n 次分解后所得的剩余图像。Di(x,y)是尺度分离后得到的尺度由小到大的较小尺度细节信息,Rn(x,y)则包含了原图像的轮廓部分,它表达了图像的基本结构、基本变化趋势部分。
1.3 基于局域波和角点检测的配准方法
1.3.1 算法的理论解析和论证
文中首先得到两幅图像的初始匹配点对,用(pAi,qBj)表示这些匹配点,其中pAi表示A图像上的第i角点,qBj表示B图像的第j角点,接着,以点pAi和qBj为中心,R为半径,定义2个邻域 N(pAi)和 N(qBj)。 如果匹配点对(pAi,qBj)是正确并且唯一的。 那么就有更多的匹配点对(n¯Ak,n¯Bl)出现在这两个邻域中,其中n¯Ak∈N(pAi),n¯Bl∈N(qBj),且点n¯Ak与点 pAi的位置关系应相似于点n¯Bl和 qBj点的位置关系;如果(pAi,qBj)不匹配,那么领域 N(pAi)和点 N(qBj)只有很少的匹配点存在,甚至没有。根据以上的匹配理论,为了得到精确的匹配结果,本文用支持强度来描述匹配过程,其表达式为:
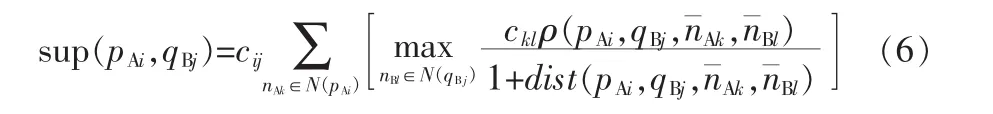
式中 cij为匹配点对(pAi,qBj)相关匹配值,ckl为(n¯Ak,n¯Bl)相关匹配值。利用式(1)计算出相关匹配系数,用dist定义这2个点对的平均距离:
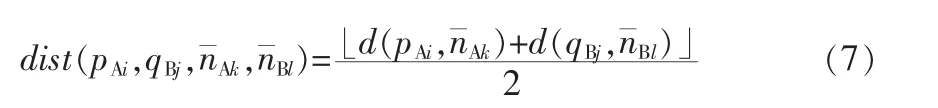
式中 d(p,n¯)是在欧式空间下点 p 与n¯的距离。 式中 ρ的表达式为:
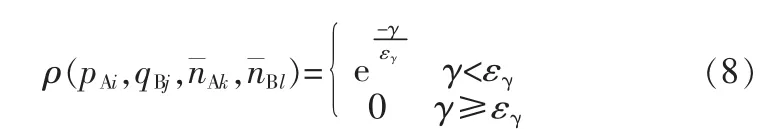
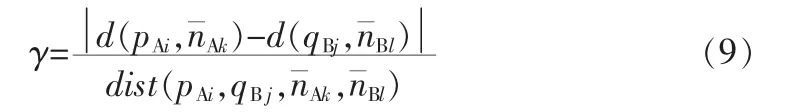
εγ为距离偏差阈值的相对值,利用式(6)可将任意一个初始匹配点的匹配强度计算出来。但是,这种方法会有一个强度不对称的问题出现,即 sup(pAi,qBj)≠sup(qBj,pAi)。 比如,在领域N(pAi)存在多个角点与领域 N(qBj)内的某一个角点匹配,则不对称问题就会出现,因此要采用双向匹配以提高配准精度。
式中γ是2个点的距离偏差相对值,其表达式为
1.3.2 算法的流程
利用上面所述方法,对两幅图像初始匹配点对的匹配强度进行计算。具体方法及实现步骤为:1)定义两个变量currentnum和next-num来判断循环条件;2)先设current-num=nextnum;3)定义一个结构类数组match-array,这个结构类中包括索引index和值value 2个变量。再定义一个变量first-maxsum,把初始匹配点集中的索引值和first-maxsum保存在结构数组match-array中;4)定义另一个变量second-maxsum,令
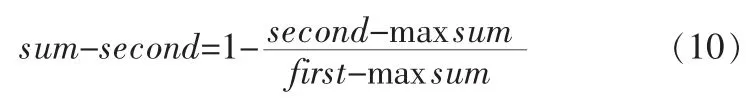
把sum-second值和这时的索引值保存在一个与matcharray一样的数组unam-match的value中;5)如果first-maxsum的值大于0,则转向步骤3)和4)执行,此时,最大强度匹配点必须从初始匹配点集中分离出来。6)此时,数组array-match和unam-match就包含了图像的匹配点对的索引和匹配强度。数组array-match中的value值是从小到大的顺序排列的,但数组unam-match不是这样,因此必须对它进行从新排列,按从大到小的顺序;7)截取数组array-match和unammatch得到新的数组。匹配这两个新数组,如果发现在arraymatch中的某个索引在与unam-match中的索引相等的情况一次,在数组believe-match中保存该索引对应的初始匹配点,并将current-num值加1;8)比较next-num与current-num,如果next-num小于current-num,则转向步骤2)~7)。通过以上计算,最终可以将一一对应的匹配点对从初始匹配点中提取出来。
2 实验结果
为了验证文中所提出的配准方法,对典型的多模态图像进行了实验。以下给出实验示例。
实验1:图2是红外图像与可见光图像的配准实验。图2(a)是可见光图像,其尺寸为300×300,即图像每行有300个像素点,共有 300行;图 2(b)是红外图像,其尺寸为 233×233;(a)、(b)之间的变换参数是已知的,旋转参数是 20°,缩放参数是0.6。以图2(b)为参考图像进行配准,得到的配准结果如图 2(c)所示。

表1 各阶段角点数目表Tab.1 Number of corner points at every stage

图2 红外与可见光图像的配准实验Fig.2 Matching experiment of infrared and visible light picture
3 结 论
文中利用局域波图像分解后的剩余图像,提出了一种基于剩余图像和角点检测的自动点匹配的多模态配准方法,在整个点匹配算法中不同阶段采取不同策略,缩短运行时间,保证计算精度。算法充分利用了剩余图像的灰度信息和角点位置信息,但没有利用到形状等区域信息和光谱信息,因此,存在大范围噪声的图像对本文的计算有一定的干扰,会增加计算量。在以后的工作中需要改进以进一步提高运算速度和准确率。
[1]倪国强,刘琼.多源图像配准技术分析与展望[J].光电工程,2004,31(9):1-6.
NI Guo-qiang,LIU Qiong.Analysis and prospect of multisource image registration techniques[J].Opto-Electronic Engineering,2004,31(9):1-6.
[2]Quddus A,Basir O.Wavelet-based medical image registration for retrieval applications[J].Proceeding of IEEE International Conference on BioMedical Engineering and Informatics,2008,2(5):301-305.
[3]刘丁,刘涵,王飞.基于最小二乘支持向量机的图像配准研究[J].仪器仪表学报,2008,29(1):124-129.LIU Ding,LIU Han,WANG Fei.Image registration based on least square support vector machine[J].Chinese Journal of Scientific Instrument,2008,29(1):124-129.
[4]姜晓彤,罗立民,赵正旭.一种改进的基于互信息和梯度特征的图像配准方法的研究[J].仪器仪表学报,2006,27(9):1141-1146.
JIANG Xiao-tong,LUO Li-min,ZHAO Zheng-xu.Improved image registration by combining mutual information and gradient information[J].Chinese Journal of Scientific Instrument,2006,27(9):1141-1146.
[5]Harris C,Stephens M.A combined corner and edge detector[C]//Proceedings of the 4th Alvey Vision Conference,1988:147-151.
[6]ZHAO Jun-long,MA Xiao-jiang,BIE Feng-feng.Fault early diagnosis of rolling element bearing based on local wave method and cyclostationarity analysis[C]//7th International Symposium on Test and Measurement,2007:3922-3925.
[7]辜小花,龚卫国,杨利平,等.核保局鉴别人脸识别算法[J].仪器仪表学报,2010,31(9):2016-2021.
GU Xiao-hua,GONG Wei-guo,YANG Li-ping,et al.Kernel locality preserving discrim inant analysis for face recognition[J].Chinese Journal of Scientific Instrument,2010,31 (9):2016-2021.
[8]Kern J,Pattichis M.Robust multispectral image registration using mutual information models[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(5):1494-1505.
[9]王富治,黄大贵.基于图像差分的精密畸变校正研究[J].仪器仪表学报,2010,31(2):377-382.
WANG Fu-zhi,HUANG Da-gui.Accurate distortion correction studybaseondifferentialimages[J].ChineseJournalofScientificInstrument,2010,31(2):377-382.

