基于FPGA的温度模糊控制器的实现
彭成功,刘艳萍,朱紫嫄
(河北工业大学 信息工程学院,天津 300401)
自1965年L.A.Zadeh教授发表了关于模糊集的开创性论文一来,模糊理论的应用,特别是在工业控制中的应用,得到了迅速的发展。与此同时,随着现代集成电路工艺技术的改进,使得在一个芯片上集成千万个器件成为可能,电子行业必将向着SOPC方向发展。20年前这个趋势已经十分明确,现在已经变成现实,15年前国内听说过Verilog硬件描述语言的不会超过几百人,更别提设计复杂数字系统了。基于现在的这个发展状况,文中基于FPGA平台使用verilog编写了一个温度二维模糊控制系统。
1 模糊控制原理
模糊控制器[1]是一种对系统控制的宏观方法,其核心是用语言描述的控制规则。语言控制规则通常用 “如果…,则…”的方式来表达在实际控制中的专家知识和经验。模糊控制的最大特点是将专家的控制经验、知识表示成语言控制规则,然后用这些规则去控制系统。其控制原理如图1所示。
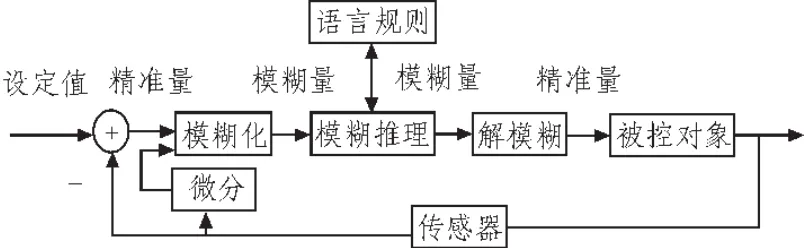
图1 模糊控制器原理示意图Fig.1 Schematic diagram of the fuzzy controller
首先通过传感器(下文用的是DS18B20)把检测到的物理信号变成精确的数字信号,精确的输入信号输入控制器后,把精确的输入量转换成为模糊集合的隶属函数,这就是所谓的模糊化,模糊化的目的是把传感器的输入转化成知识库可以理解和操作的变量格式;然后,根据专家的经验制定出模糊控制规则,并进行模糊推理,得到一个模糊输出集合;最后,根据模糊推理得到输出模糊集合隶属函数,用恰当的方法找一个具有代表性的精准值作为控制量,去控制被控对象。
2 模糊控制器的设计
2.1 模糊控制器的设计思想
模糊控制器有一维,二维和多维,维数越多精准度越高。但随着维数的增加,模糊规则的确定会更加困难,控制算法会趋于复杂化[2]。基于这些原因,我们设计使用最广的二维模糊控制器。
设计分为3部分:
1)语言控制规则
2)隶属函数
3)控制器输入输出规范化的比例因子
在设计一套语言规则时,必须要考虑它的完整性、交叉性和一致性[1]。
2.2 模糊控制器的设计过程
下面来具体设计一个用于控制温度的模糊控制器,系统顶层模块如图2所示。ROM输入端口的地址信号。温度偏差(error)=设定温度-测量温度,温度偏差变化率(rate)=(此刻测量温度-上一时刻的测量温度)/时间间隔,取时间间隔为1 s,即 rate可由此刻测量温度-前一秒的测量温度来衡量。设置温度区间为40~45°C,测量温度范围为 25~45 °C,即 error的论域 E 位-5~20 °C,把E论域划分为10个模糊子集,分别用模糊言语表示N(负)、ZO(零)、P0(正 0)、PVS(正很小)、PS(正小)、PMS(正中小)、PM(正中)、PMB(正中大)、PB(正大),PVB(正很大),他们的对应关系见表1;把rate的论域RT划分为9个模糊子集,同样也用模糊语言表示 NMS(负中小)、NS(负小)、NVS(负很小)、N(负)、ZO(零)、P0(正 0)、PVS(正很小)、PS(正小)、PMS(正中小)他们对应关系如表2所示。
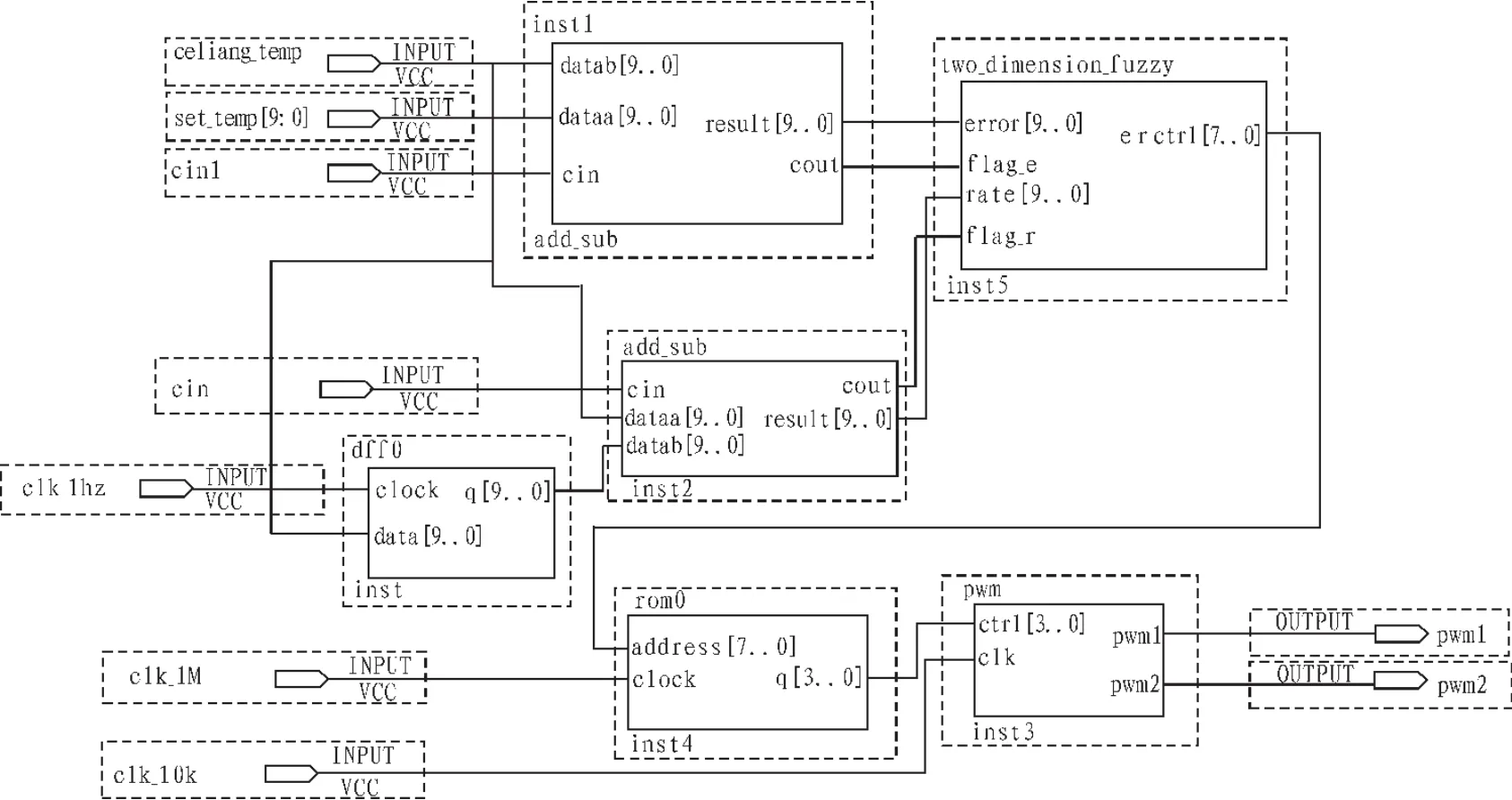
图2 模糊控制器系统顶层框图Fig.2 Top-level block diagram of the fuzzy controller system

表1温度偏差模糊化表Tab.1 Temperature deviation fuzzification table

表2温度偏差变化率模糊表Tab.2 Fuzzy table of the rate of change of temperature deviation
由于DS18B20提供的温度测量精度是9到12位,在这里设定的温度范围中只用到10位就可以表示 (具体可参看DS18B20手册),该模糊算法子模块的设计程序和仿真结果(如图3所示)如下:
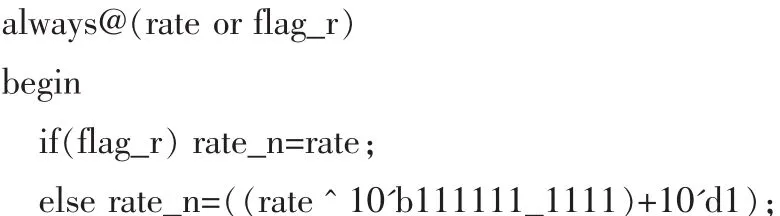


PWM波生成子模块的2个输入分别是频率为10Khz的时钟信号和控制占空比的信号,2个输出分别是几何对称的PWM波[8],他们之间有一定的死区(最大的占空比为40%),这是为了避免功率放大电路MOS管的全部导通。
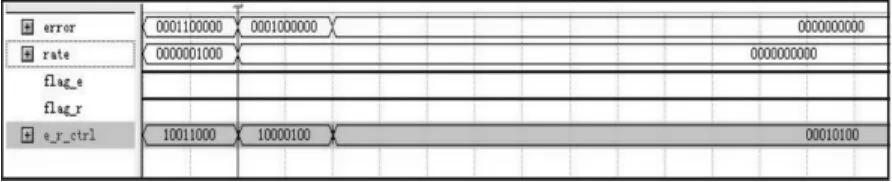
图3 模糊算法子模块仿真图Fig.3 Simulation result of the fuzzy algorithm sub-module
该模糊算法子模块的设计程序和仿真结果如图4所示。

图4 PWM波生成子模块仿真图Fig.4 Simulation result of the PWM waves sub-module
ROM宏模块的2个输入分别是1 MHz的时钟信号和模糊控制算法子模块中的e_r_ctrl信号,输出是控制占空比的信号。
下面来分析一下ROM存储器初始化 (.MIF)文件的设计,首先,把占空比ratio的论域 RT[0,40%]划分成 9个模糊子集,它们的应用关系如表3所示;然后,我们设计出温度偏差(E)、温度偏差变化率(RT)和占空比控制信号(R)之间的模糊语言控制规程,如表 4所示(表中内容为 R);最后,以error(高4位)和rate(低四位)为ROM的输入地址信号。
该ROM的初始化文件程序和仿真结果如图5所示。

表3 Ratio的模糊规则表Tab.3 Ratio fuzzy rule table
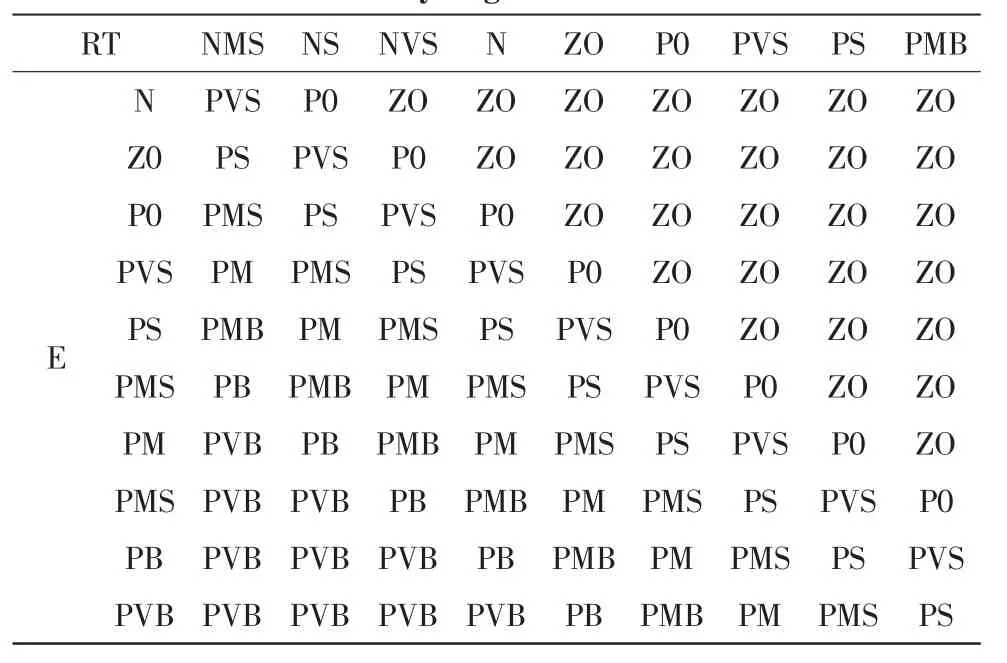
表4 模糊语言控制规则Tab.4 Fuzzy linguistic control rules
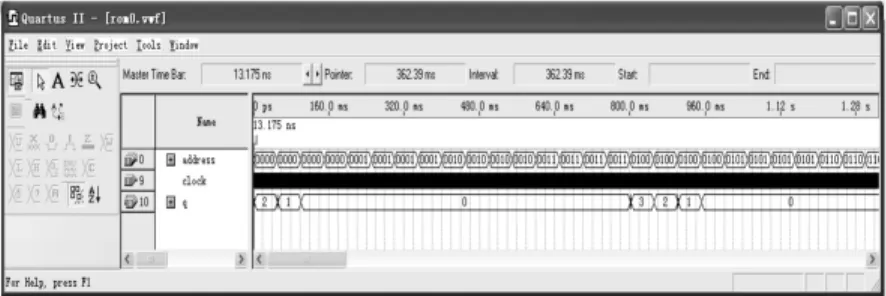
图5 ROM模块的仿真图Fig.5 ROM module simulation figure
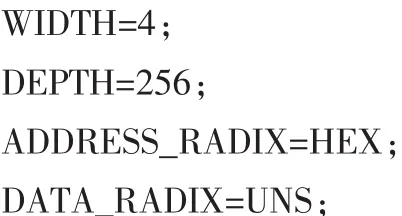


加减法模块有3个输入分别是cin、dataa、datab,输出为温度偏差或温度偏差变化率(这里用到了2个加减法子模块)。
加减法子模块的在cin为0和1情况下的仿真图,如图6、7 所示。

图6 cin=1的仿真图Fig.6 Simulation of the cin=1
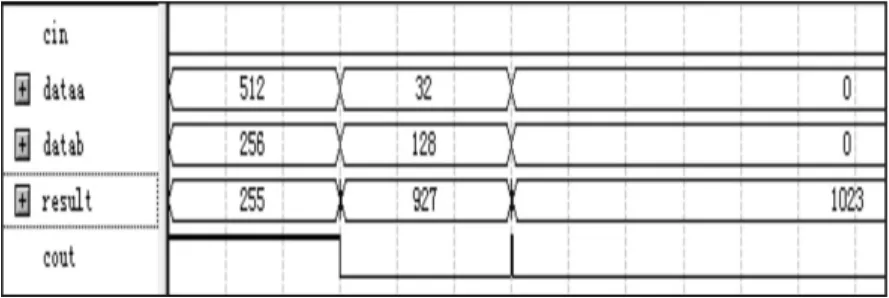
图7 cin=0的仿真图Fig.7 Simulation of the cin=0
数据寄存器宏模块有2个输入分别是1 Hz的时钟信号(在前面温度偏差变化率计算值,时间间隔为1 s)和测量温度信号,输出为延时了一个时钟周期的测量温度信号。
模糊控制器顶层模块仿真结果如图8所示。
对仿真结果的分析如下:
当前的测量温度为1001000000(36°C),前一时刻测量温度为 1000111100(35.75 °C),温度偏差变化率为 0.25 °C,设置的温度为1010100000(42°C),根据模糊规则表可知,对应的R域为PS,也就是15%,实验结果正好为15%。
模糊数的隶属函数可以取各种不同的形状,如梯形、三角形、钟形、棒形。其中棒形最为简单,是其它隶属函数幅宽为零时的特例。三角形的隶属函数,形状简单,容易计算,并且和其它较复杂的隶属函数得到的控制结构差别很小,故别广泛应用。棒形的隶属函数,可以省去计算较为复杂的求重心的部分,这样整个控制器的计算就非常简单,因而在实际应用中,便于计算的实现。
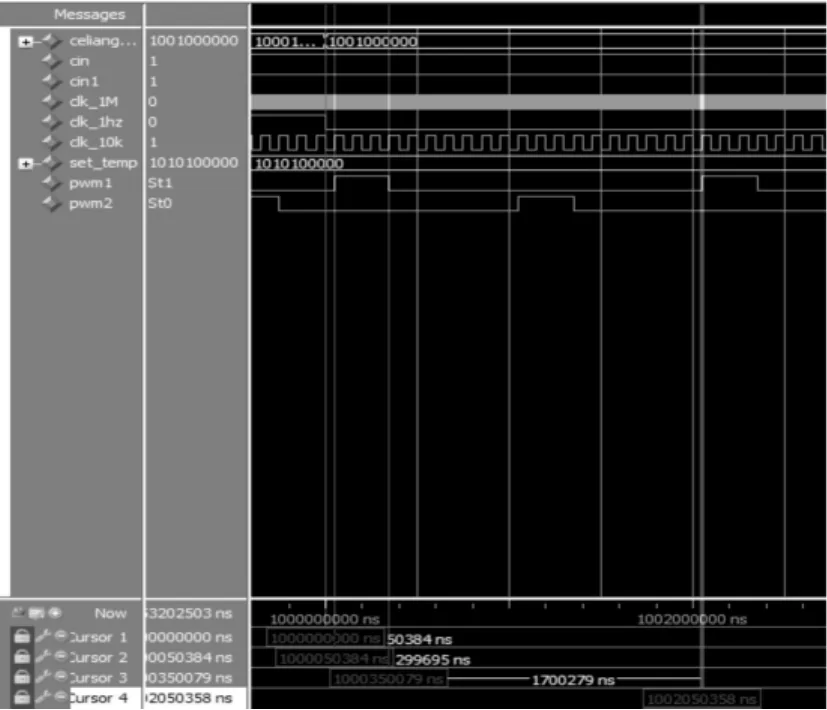
图8 模糊控制器顶层模块仿真结果Fig.8 Simulation results of the fuzzy controller top-level module
在这个设计中,使用三角形的隶属函数来表示控制规则条件部分的模糊数,用棒形的隶属函数来表示结论部分的模糊数。
3 结束语
基于FPGA平台设计的温度二维模糊控制器,充分利用了FPGA的优势,设计结果可行,能够应用到温度监控系统中。
[1]赵振宇,徐用懋.模糊理论和神经网络的基础与应用[M].北京:清华大学出版社,1996.
[2]诸静.模糊控制理论与系统原理[M].北京:机械工业出版社,2005.
[3]夏宇闻.Verilog数字系统设计教程[M].北京:北京航天航空大学出版社,2008.
[4]周景润,图雅,张丽敏.基于Quartus II的FPGA/CPLD数字系统设计实例[M].北京:电子工业出版社,2007.
[5]Cyclone II Device Halldbook[S].AlteraCorporation,2008.
[6]EDA先锋工作室.Altera FPGA/CPLD设计(基础篇)[M].北京:人民邮电出版社,2005.
[7]EDA先锋工作室.Altera FPGA/CPLD设计(高级篇)[M].北京:人民邮电出版社,2005.
[8]秦艳平,李斌,梁俊龙,等.[J].火箭推进 ,2012(5):7-12.
QIN Yan-ping,LI Bin,LIANG Jun-long,et al.Control-oriented research on dynamic characteristics of fuel regulator[J].Journal of Rocket Propulsion,2012(5):7-12.

