等物质的量规则的应用——对武汉大学主编《分析化学》(第5版)的建议

赵建宏 赵梦月

(郑州大学化工能源学院 河南郑州 450002)

武汉大学主编的《分析化学》(第5版,2010年11月第12次印刷)教材(以下简称“第5版教材”)，内容丰富新颖，印刷精良，不愧优秀教材的称号。正因为它是国内应用最广、影响力最大的教材，对它更应该严格要求。下面就该教材滴定分析计算的内容谈一些看法，供编著者参考。

在该书中介绍了氧化还原及酸碱滴定结果计算的等物质的量规则表示式，如：

(1)

并列出了等物质的量规则常用到的基本单元与浓度的关系式：

(2)

等物质的量规则[1-3]自提出以来，经过我国化学家的共同努力，现在已被广泛应用。我们发现，已有数十部高校教材[4-7]、专著[8-10]、手册[11]以及有关的国家标准[12-17]都应用了等物质的量规则。在武汉大学主编的《分析化学》第3版中就介绍应用了等物质的量规则，对这个规则的普及起了重大作用。但第5版教材的作者认为“计量数比法可以方便地进行各种有关计算”，而没有在滴定分析计算中进一步应用等物质的量规则。实际上，对于一些复杂的滴定体系,应用计量数比法是很困难的。如果利用等物质的量规则来处理教材中有关问题，不仅能使滴定分析计算更简单，且能使某些内容的表述更严格，更科学。

1 关于滴定度

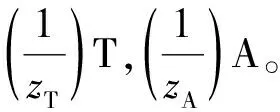
(3)

式(3)在滴定分析结果计算中广泛应用，因此我们称其为等物质的量规则的实用通式。该式不仅表示反应物的基本单元物质的量相等，也可表示得或失电子的物质的量(氧化还原反应)，得或失质子的物质的量(酸碱反应)及两离子的电荷相等(沉淀反应)。

(4)

(5)

将式(4)和式(5)代入式(3),可得滴定度(T(A/T))的计算式：

(6)

利用式(6)很容易求出第5版教材18页例7中K2Cr2O7对Fe、Fe2O3、Fe3O4的滴定度为：

(7)

(8)

(9)

显然,利用式(6)计算滴定度比第5版教材上的方法更简单。

2 有关换算因数问题

2.1 教材中换算因数的定义不够严格

第5版教材在283页给出了换算因数的定义：“待测组分的摩尔质量与称量形式的摩尔质量之比是常数，通常称为换算因数”。当称量形式与待测组分的化学式中目标元素原子个数相同时，这个定义才是正确的，如教材中列出的Cl与AgCl，S与BaSO4;否则就不正确，例如FeO与Fe2O3，MgO与Mg2P2O7。利用等物质的量规则很容易导出一个简单的计算换算因数通式。

2.2 化合物的等物质的量规则

为导出换算因数计算式，首先讨论同一元素形成的不同化合物之间的等物质的量规则。等物质的量规则不仅可用于化学反应体系中各物质之间的物质的量关系，也可表示一定量的某元素形成一系列化合物之间的物质的量关系。例如，对于一定量的铁生成的不同化合物Fe、Fe2O3、Fe3O4，选取含有一个铁原子的特定组合为基本单元，即:

(10)

据物质的量的定义，有：

(11)

因此，对于一定量的某一元素形成的系列化合物，只要选取的基本单元含有相同个数该元素原子，那么，这些基本单元的物质的量就相等。我们称其为化合物的等物质的量规则。

2.3 换算因数的导出

利用化合物的等物质的量规则很容易导出换算因数，如果上述3个含有铁元素的物质，质量分别为m(Fe)、m(Fe2O3)、m(Fe3O4)，据式(4)可将式(11)变为:

(12)

则有：

(13)

(14)

显然，在同一元素的不同化合物之间建立等物质的量关系时，其基本单元的摩尔质量之比即为其换算因数。

2.4 分析结果中质量分数的换算

实际上,换算因数不仅用于重量分析中由称量物质的质量求算待测物质的质量，在任何分析方法结果的表达中，同一元素的不同化合物的质量分数都可用它来换算。例如第5版教材18页的例5，已知w(Fe)求w(Fe2O3)。对此，只要将式(13)两端同除以矿样质量ms，则有：

(15)

利用上式求w(Fe2O3)，仅用一行就可算出结果，而在第5版教材中却用了7行的篇幅。

由于换算因数不仅用于重量分析而且在滴定分析中也要涉及，因此建议将这部分内容由重量分析提前至容量分析。

3 滴定分析结果计算的规范化和简单化

等物质的量规则能使滴定分析结果计算简单化(通常不必书写反应方程式)及规范化(有统一的计算公式及程序)。下面以第5版教材257～260页的例题为例来说明这一问题。

3.1 关于第5版教材258页例15的计算

第5版教材258页所列计算式为：

显然，该式的计算结果中带有体积单位“升”(L)。之所以发生上述错误，是因为以上计算式中的m(KIO3·HIO3)应为滴定度T(KIO3·HIO3/Na2S2O3)。

若使用等物质的量规则及滴定度的计算式处理此问题，则过程既简单又不会发生上述错误。据式(3)，体系中待测物质的基本单元与滴定剂基本单元的物质的量关系式为：

(16)

则有：

(17)

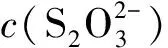
(18)

而

(19)

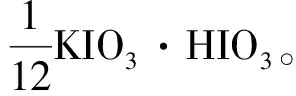
3.2 关于第5版教材258页例16的计算式单位

在第5版教材258页的计算式中，分子项10-3之后应加上L·mL-1,否则结果中就会出现mL·L-1。

另外， 如果用等物质的量规则求解此题,就不必写繁杂的反应式,仅据体系中氧化剂及还原剂得失电子的物质的量相等,即可写出下列的关系式:

(20)

则有：

3.3 关于第5版教材259页例18的等物质的量规则解法

据等物质的量规则可写出下列等式：

(21)

则有：

显然，利用等物质的量规则比第5版教材260页的解法2还要简单。

3.4 等物质的量规则能使复杂滴定分析计算简单和规范

从以下两个例子可以进一步看出，等物质的量规则能使复杂滴定体系的计算像简单体系一样简单和规范。

例1同一元素形成一系列化合物的体系。

以Pb3O4含量的测定实验为例。将Pb3O4样品(样品质量为ms)溶于HCl溶液中，再加入K2Cr2O7溶液，使Pb2+完全沉淀为PbCrO4，过滤沉淀，将沉淀溶于HCl溶液，加入KI溶液，然后用浓度为c(Na2S2O3)的标准Na2S2O3溶液滴定生成的I2，消耗的体积为V(Na2S2O3)，求Pb3O4的质量分数。

解据等物质的量规则及体系中氧化剂与还原剂得失电子相等的原则，体系中各物质的基本单元的等物质的量关系为：

(22)

即滴定剂与待测物的关系为：

(23)

则有：

(24)

在两篇计量数比值法提倡者[18-19]的文章中都把上述例题作为例子。但在他们提供的解法中都要先写出5个配平的化学反应式，然后再一步一步地找出各个物质的计量关系，这显然要比等物质的量规则麻烦得多，也复杂得多。

例2反应体系中包含两个还原剂及歧化反应。

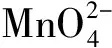
解等物质的量规则实用式可表示反应中氧化剂得电子的物质的量与还原剂失电子的物质的量相等。即：

(25)

则有：

(26)

(27)

如果用计量数比值法对这个问题进行计算[20],需在这个体系5个反应式中，找出有关物质的计量关系。由于含有歧化反应，这个过程非常复杂。

从以上例题可以看出，对于任何复杂的滴定体系，应用等物质的量规则都能简单、规范地计算滴定结果；然而用计量数比法却往往会遇到困难，因为复杂反应中的反应步序多，对每一步都要计算计量数比值，从而使计量数比法的实际应用受到限制。这也是我们推荐等物质的量规则的原因。

4 有关符号“～”的讨论

在第5版教材中用符号“～”表示滴定体系中各物质的计量关系，如257页列出的通式：

aX～bY～…～cZ～dT

aX～dT

(28)

又如257页例14中有：

(29)

这种表示计量关系的方式不符合国家标准(GB3101—93)[21]及国际标准(ISO31—11:1992)[22],这些标准规定“～”是数字范围的符号。

实际上，应用等物质的量规则能准确地表示反应体系中各物质的计量关系。如式(28)和式(29)可表示为：

Δn(aX)=Δn(bY)=…=Δn(cZ)=Δn(dT)

(30)

Δn(aX)=Δn(dT)

(31)

(32)

(33)

实际上，这是根据配平的化学方程式，将反应物的化学式与其计量数一起作为基本单元而建立的等物质的量规则表示式。我们称其为等物质的量规则的基础式。这些表示式完全符合国家标准及国际标准，而且计量数比法所用的计算公式也能由式(31)导出：

(34)

(35)

即:

(36)

因此，对于仅习惯用计量数比进行滴定结果计算者，不妨用式(30)和式(31)表示体系中各物质的计量关系。

5 关于“系数”问题

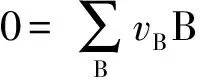
6 教材应介绍使用化学分析国家标准

国家已发布了化学分析的标准，例如：《GB/T601—2002 化学试剂 标准滴定溶液的制备》[12]，《GB/T602—2002 化学试剂 杂质测定用标准溶液的制备》[13]，《GB/T603—2002 化学试剂 试验方法中所用制剂及制品的制备》[14]。

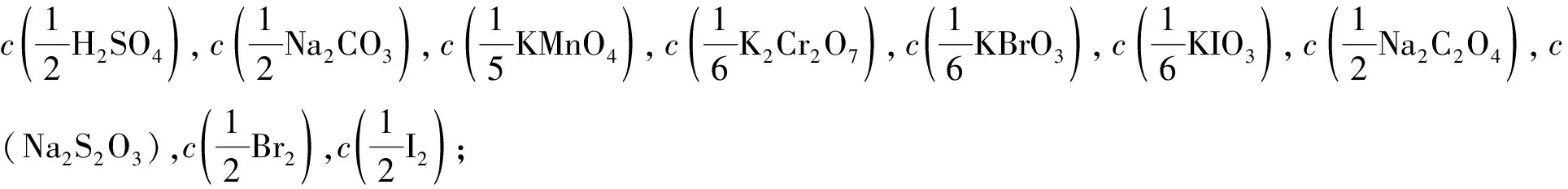
在这些标准中，滴定结果的计算也全部应用了等物质的量规则的方法，例如，用标准硫代硫酸钠溶液标定重铬酸钾溶液，其计算式为：

凡涉及到化学分析的各种工业标准都须根据这些标准来制定，我们查找到的工业标准[15-17]都符合这些标准的规定，例如在《GB/T15456—2008 工业循环冷却水中化学需氧量(COD)的测定》中,COD的等物质的量规则计算式为：

分析化学工作者必须熟悉这些分析化学标准。分析化学教材是为将来的分析化学工作者学习时使用，因此在教材中应介绍这些标准并把这些标准作为参考资料提供给学生。

参 考 文 献

[1] 赵梦月.化学通报,1986(5):48

[2] 赵梦月,吕灵翠.化学通报,1992(3):13

[3] Zhao M,Lu L C.AnalChimActa,1994(289):121

[4] 李克安.分析化学教程.北京:北京大学出版社,2005

[5] 彭崇慧,李克安.定量分析简明教程.第3版.北京:北京大学出版社,2009

[6] 邹明珠.化学分析.第2版.吉林大学出版社,2001

[7] 吴性良,张继烈.分析化学原理.第3版.北京:化学工业出版社,2010

[8] 宋卫良.冶金化学分析.北京:化学工业出版社,2008

[9] 徐伏秋,杨刚宾.硅酸盐分析.北京:化学工业出版社,2009

[10] 姜洪文.化工分析.北京:化学工业出版社,2008

[11] 张铁垣.化验室工作实用手册.北京:化学工业出版社,2008

[12] GB/T601—2002 化学试剂 标准滴定溶液的制备

[13] GB/T602—2002 化学试剂 杂质测定用标准溶液的制备

[14] GB/T603—2002 试验方法中所用制剂及制品的制备

[15] GB14888.1—94 食品添加剂 新红

[16] GB17512.2—1998 赤藓红铝色淀

[17] GB/T15456—2008 工业循环冷却水中化学需氧量(COD)的测定

[18] 李俊义.杭州师范学院学报,1987(1):1

[19] 李树伟.大学化学,1998(3):24

[20] 李克安.北京大学分析化学课件,jingpinke/resource/recommended

[21] GB3101—93 物理科学和技术中使用的数学标志与符号

[22] ISO31—11:1992 物理科学和技术中使用的数学标志与符号

[23] GB3102.8—1992 物理化学及分子物理学的量和单位

[24] ISO31/8—1992 物理化学及分子物理学的量和单位