基于T-S模糊模型的电液比例位置控制系统研究

杜 进，胡金池，彭 琦，李 明

（1.西南林业大学 云南 昆明 650224；2.三一重工 黑龙江 哈尔滨 150000）

近年来，随着电液比例控制技术的发展，凭借着成本低、抗污染能力强等优点，在许多场合逐渐替代了伺服阀，特别是在大型的工程机械中的应用越来越广泛。电液比例阀能同时实现流量和方向以及压力的控制，并且可以方便地实现计算机控制。但由于电液比例阀的死区和非线性的特征使其控制要比伺服阀难以控制，而传统的PID控制由于参数整定困难，工程上很难得到满意控制效果[1-3]。而T-S模糊模型其本身就是一种非线性的模型，其基本思想是将非线性系统根据实际的情况在合适的工作点对系统进行局部线性化，然后依照相应的解模糊方法对每个线性的输出结果进行整合，最后输出系统的控制量，从而实现对非线性系统的控制。

1 系统组成及原理

电液比例位置控制系统主要由油箱1、油缸7、位移传感器8、电液比例阀6、单向阀4、液压泵3、溢流阀5、比例放大器10、滤油器2和计算机9组成。系统在工作时，位移传感器感应出活塞的位置，然后通过数据采集卡将感应到的信号采集并传递给计算机，计算机根据当前信号和目标信号计算出误差的大小和误差变化率的大小，模糊化程序对误差和误差变化率进行模糊化处理，将其转化为T-S模糊控制器能够识别的信号，然后将模糊化的结果传递给模糊规则库，推断出模糊输出，并将模糊输出进行解模糊得到精确的控制量。通过比例放大器对控制量进行放大，最后将放大的信号输给电液比例阀，控制电液比例阀的阀口开度以实现对电液比例系统的流量和压力的控制，进而实现液压缸的精确控制。其主要的硬件组成如图1所示。

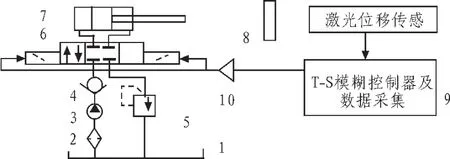
图1 电液比例位置控制系统Fig.1 Electrohydraulic proportional position control system

2 电液比例阀控液压缸的数学模型

2.1 阀控缸的模型

本系统采用的电液比例阀是零开口四边滑阀，4个节流窗口是匹配且对称的；由于阀腔容积很小，因此，不考虑油液在阀腔内的压缩。并且阀的响应速度快，即阀芯位移及外负载变化立即会引起负载流量的变化[4]。零开口四边滑阀的线性流量方程，液压系统的流浪连续方程，由牛顿第二定律推导出的力平衡方程可写成：

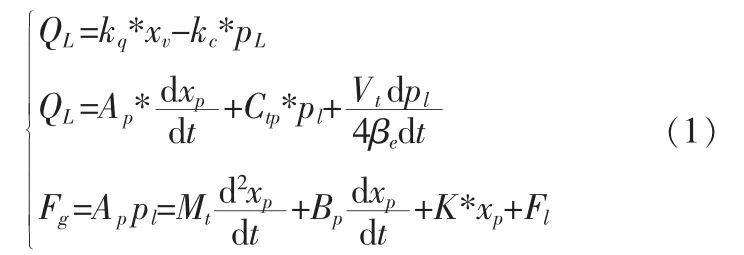
由于本系统没有负载，因此K=0，并且流量—压力系数kce很小，粘性摩擦系数Bp也很小，并且本系统是无负载系统，因此（1）式进行拉氏变换并整理可得：

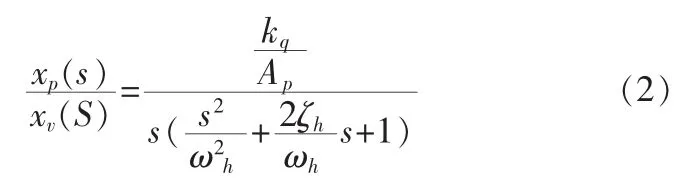
2.2 电液比例阀的传递函数

根据实验得到电液比例阀是一个积分环节与一个二阶震荡环节的叠加，其传递函数为：

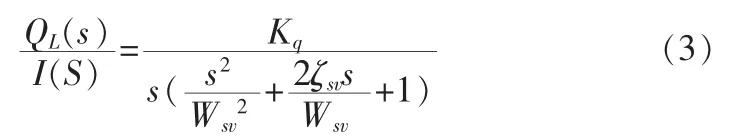
2.3 位移传感器和比例放大器的传递函数

由于电液比例放大器的转折频率比系统的频宽要高得多，因此电液比例放大器可以视为比例环节。位移传感器的频宽也比系统的频宽要高很多，因此位移传感器也被看成一个比例环节，位移传感器和比例放大器的传递函数为：

2.4 电液比例位置控制系统的传递函数

由（1）～（3）式可以得出电液比例位置控制系统的系统方框图，如图2所示。

图2 电液比例位置控制系统框图Fig.2 Electrohydraulicproportionalpositioncontrolsystemblockdiagram

由图2可以推导出电液比例位置控制系统在任何状态下的传递函数：

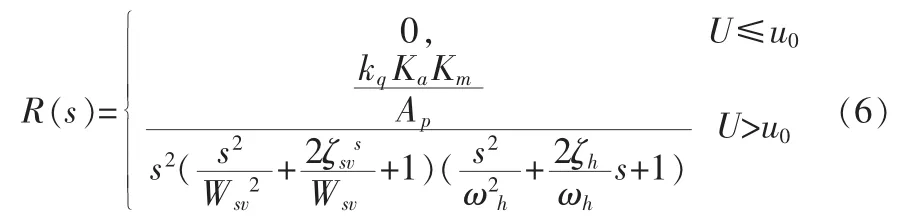
当输入的控制电压U小于或等于电液比例阀的开启电压u0时，液压缸没有动作。当U大于电液比例阀的开启电压u0时，系统则变成一个非线性的控制对象。

2.5 主要参数

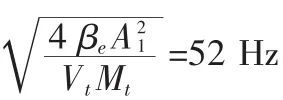
3 模糊控制器的设计

T-S模糊模型是由Takagi和Sugeno于1985年提出的，T-S模糊模型由模糊化、规则库、推理机、解模糊几个部分组成，如图3所示。当控制系统有输入信号时，模糊化模块将输入信号进行模糊化处理，将输入信号变成模糊控制器能够识别的信号，即模糊矩阵A。然后模糊矩阵A依照编写的模糊规则和模糊推理产生模糊矩阵B。模糊矩阵B就是系统模糊输出，但此输出还不能被液压系统识别，故而还要设计出能让液压系统识别的信号，即解模糊过程。通过对模糊矩阵的整合就可以得到模糊控制器对液压系统的控制信号[5]。

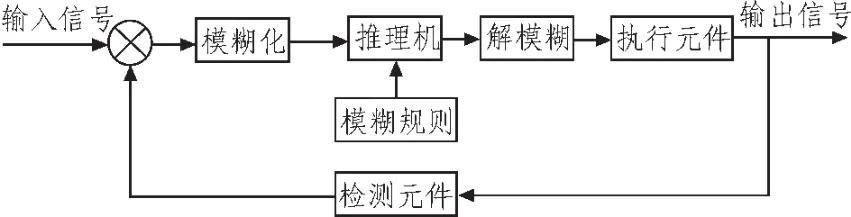
图3 系统闭环控制结构图Fig.3 Closed-loop control structure diagram

3.1 隶属度函数的确定

隶属度函数是模糊控制器能够运行的基础，正确构造隶属度函数对模糊控制器的控制效果有关键性的作用。但到目前为止还没有一套成熟有效的方法，大多数隶属度函数的确定都是基于经验和系统本身特点的。本研究对象为电液比例位置控制系统，为了方便数字信号的实现以及系统本身的特点和算法的效率，文中选择三角形的隶属度函数。

根据一般设计控制器的经验来说，为解决系统响应速度和系统稳定性的矛盾。在设计控制器时，在误差和误差变化率较大时，适当地增大控制器的输出，提高系统的响应速度。在误差和误差变化率较小时，适当地减小控制器的输出，增强系统的稳定性[6]。在T-S模糊控制中，采用变更各个模糊子集对应的模糊规则数目来解决系统响应速度和稳定性的矛盾。换而言之，即在误差和误差变化率较大的区域对应较少的模糊规则数目，以提高系统的响应速度。在误差和误差变化率较小的区域对应较多的模糊规则数目，以提高系统的稳定性。为使论域中任何一点对应的隶属度值不能太小，这里使隶属度的值域为[0.2，1]。因此，隶属度函数如图4。隶属度函数中可以看出，共分为8个模糊等级。为解决在同一个模糊等级中出现不同元素对应同样的隶属度的情况，需要对模糊等级左右两边进行区分。如图所示，在相邻的两个隶属度等级中会出现公共元素对于这些公共元素，在本研究中将其归于前一个隶属度等级里面。例如:-7属于NSS，-5属于NB，以此类推。

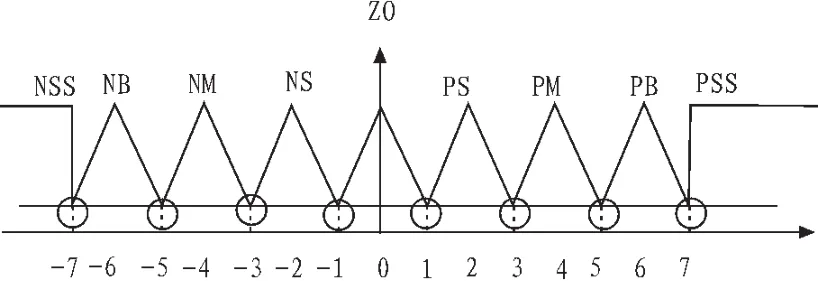
图4 隶属度函数图Fig.4 Membership function diagram

本系统所采用的隶属度函数可以写为：

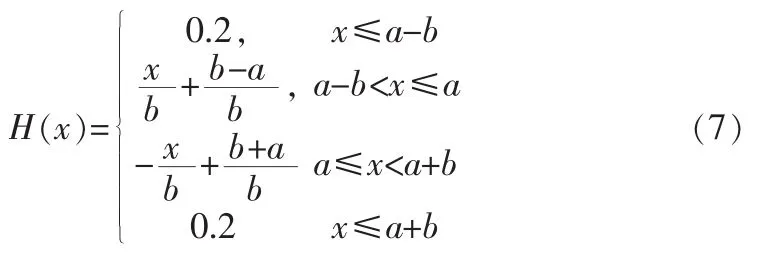
3.2 模糊规则库的设计

模糊规则库是模糊控制器的关键部分，当前还没有权威的理论来指导模糊规则库的构建，现在在模糊规则库的构建中一般都是从系统本身的特点出发或者根据多年的经验来指导构建的[7]。这里在构建模糊规则库采用前一种方法。本系统由两个部分构成，一个部分是没有陷入死区时候系统的非线性部分另一个部分为系统输入信号太小，导致输出电压不足以逃出系统的死区，从而出现了有输入而没有响应的情况出现。对于这两种情况需要区别对待。首先，当系统没有进入死区的时候，即此时的系统就为一个非线性系统。其次，当系统陷入死区的情况。对于非线性部分的模糊规则库由前件和后件组成，其形式为：

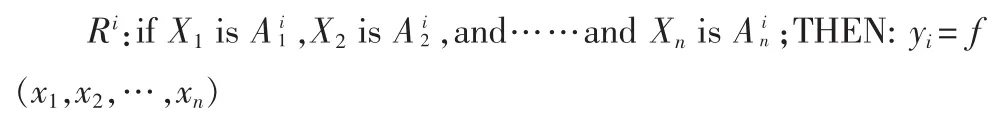
当系统没有陷入死区，对于模糊规则库的前件，前件的作用就是将模糊化后的信号进行分类，并确定隶属度的大小[8]。模糊前件对模糊化后的信号进行划分的指标有以下几个：模糊化后的隶属等级、在隶属等级中的位置、误差的隶属度、误差变化率的隶属度。

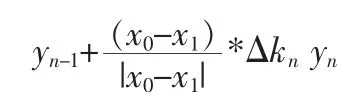
bn为第n条模糊规则所对应的步长，这个步长是通过实验得到的。Hi为第i条规则所对应的信号的适合度。适合度的算法为：Hi=ui（e）∧ui（ec）ui（e）为第 i条规则对应信号误差的模糊子集，ui（ec）为第i条规则对应信号误差变化率的模糊子集。从模糊后件的形式可以看出，模糊控制器的每一个模糊输出都是线形的。当系统是非线性时，模糊控制器用线性的输出来逼近非线性的对象。

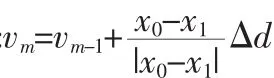
模糊规则库的设计由非线性部分的模糊规则和死区部分的模糊规则构成。当系统在非线性部分的时候，模糊控制器的模糊输出是用线性规则对非线性的近似。当系统进入死区时，死区模糊规则开始运行，对输出信号进行校正，跳出死区。

3.3 解模糊

为了使电液比例系统能够识别模糊控制器的信号要对信号进行处理，即将模糊信号转化为精确的控制信号。根据电液比例位置控制系统的特点我们采用重心法解模糊。其具体的表达如下：

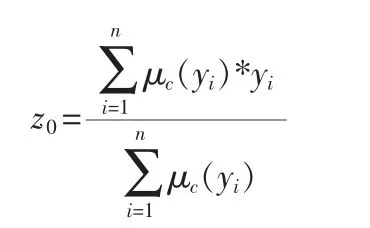
通过解模糊的方法就可以得到给到控制电压大小，再进行D/A转换将数字信号转换成模拟信号即控制电压，进而控制电液比例阀的阀口开度，从而改变了系统的流量以及系统压力，以达到精确定位的目的。

4 仿真实例

为了验证基于T-S模糊模型的电液比例位置控制系统的控制效果，在Matlab中建立电液比例位置控制系统的模型进行仿真实验。 参考模型的传递函数为：d=sin（i）*cos（i）。

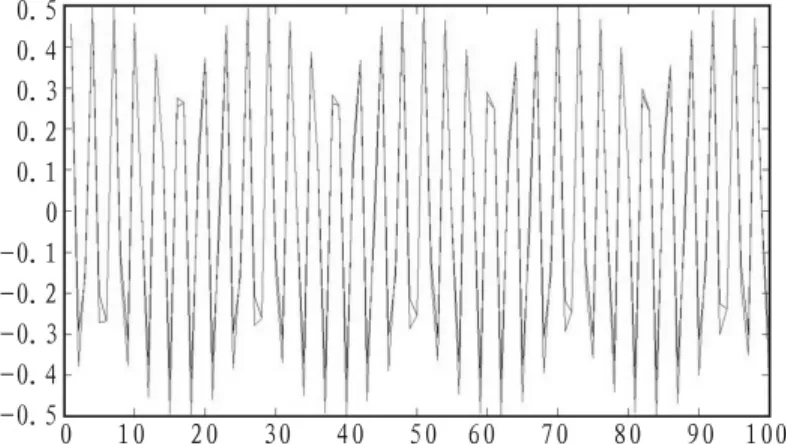
图5 电液比例位置控制系统输出曲线Fig.5 Electrohydraulic proportional position control system output curve

本次仿真对于每个目标值都是进行300次逼近得到的结果。从仿真图中可以看出系统的误差变化是周期性的，其原因在于输入信号也是周期变化的。

5 结 论

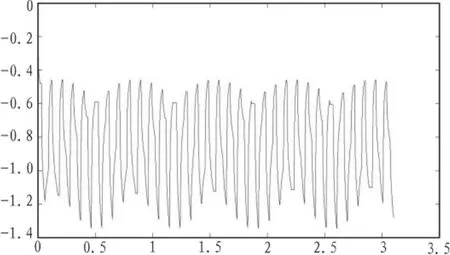
图6 T-S模糊控制器输出曲线Fig.6 T-S fuzzy controller output curve

本文针对电液比例位置控制系统的死区和非线性的问题，采用T-S模糊模型的方法建立了基于T-S模糊模型的电液比例位置控制系统，根据对电液比例位置控制系统的特点编制相应地模糊规则，并不断的完善这些规则，使电液比例位置控制系统能够越过死区。虽然通过仿真实验验证了系统的性能，并取得了较好的效果。但为了是系统的控制效果更加理想可以增加模糊规则的数目，但随着模糊规则的数目的增加系统的变得更加复杂，从而降低了系统的响应速度。为此，怎样用较少的模糊规则数目使系统的控制效果变好还有待于进一步的研究。

[1]郑江，陈柏金.电液比例位置控制系统的参数自整定Fuzzy-PI控制[J].液压与气动，2003（5）：33-35.

ZHANG Jiang，CHEN Bai-jin.Electrohydraulic proportional position control system with parameter self-tuning Fuzzy-PI control[J].Hydraulic and Pneumatic，2003（5）：33-35.

[2]朱银法，陈冰冰，安磊.电液比例位置控制系统的自整定模糊PID控制研究[J].机床与液压，2010，38（8）：98-100.

ZHU Yin-fa，CHEN Bing-bing，AN Lei.Electrohydraulic proportional position control system with self-tuning fuzzy PID control research[J].Hydraulic and Pneumatic，2010，38（8）：98-100.

[3]赵瞻，郭淑娟.基于电液比例位置系统的模糊自整定PID控制器[J].机电工程，2006，23（11）:59-62.

ZHAO Zhan，GUO Shu-juan.An electro-hydraulic proportional position control system based on fuzzy self-tuning PID controller[J].Mechanical and electrical engineering，2006，23（11）:59-62.

[4]常钰，冯永保.电液比例阀控缸速度控制系统的建模与仿真[J].液压气动与密封，2011（8）:23-28.

CHANG Yu，FENG Yong-bao. The electro-hydraulic proportional speed control system modeling and simulation[J].Hydraulic and Pneumatic Seals，2011（8）:23-28.

[5]孔德永，高永琪.T-S模糊控制在飞行器滚动通道设计中的应用研究[J].弹箭与制导学报，2009，29（4）:19-24.

KONG De-yong，GAO Yong-qi.T-S fuzzy control in aircraft rolling channeldesign applied research[J].Journalof Projectiles and Guidance，2009，29（4）:19-24.

[6]赵贤林，沈明霞.基于Delta算子系统T-S模型的鲁棒稳定性研究[J].控制工程.2007，14（1）：60-63.

ZHAO Xian-lin，SHEN Ming-xia.Based on theDelta operatorsystems robuststability ofT-S model[J].Control Engineering，2007，14（1）：60-63.

[7]宋金泽，戴斌，崔慧海，等.基于T-S模糊模型的LQR控制器设计[J].计算机仿真，2009，26（11）:174-177.

SONG Jin-zhe，DAI Bing，CUI Hai-hui，et al.Based on T-S fuzzy model of LQR controller design[J].Computer Simulation，2009，26（11）:174-177.

[8]陈学有，赵志伟，尹柳.基于随机负荷与模糊线性规划的可伸缩静态安全域[J].陕西电力，2012（6）：43-48.

CHEN Xue-you，ZHAO Zhi-wei，YIN Liu.Flexible steadystate security region of power system with stochastic load demand and fuzzy linear programming[J].Shaanxi Electric Power，2012（6）：43-48.