一种改进的神经网络相关性剪枝算法

李小夏，李孝安

（西北工业大学 计算机学院，陕西 西安 710129）

神经网络剪枝算法就是在神经网络训练好之后，以一定的标准或者允许误差，删除不重要的网络节点以及网络中部分节点连接的算法[1]。通过剪枝算法，能够使得神经网络的结构得到简化，计算性能（如计算时间）得到优化，同时为神经网络的后期处理，比如神经网络的知识提取等要求网络功能齐全，结构简单的操作打下基础，以防止由于网络结构复杂，造成计算出现组合爆炸的问题[2]。

当前的剪枝算法大致分为3类：1）权衰减法[3]：权衰减法属于正则化方法，它通过在网络目标函数中引入表示结构复杂性的正则化项来达到降低网络结构复杂性的目的。2）灵敏度计算方法[4]：灵敏度计算方法是指在网络进行训练时或在网络训练结束后，计算节点（输入节点以及隐层节点）或连接权对网络误差的贡献（灵敏度），删除那些贡献最小的节点或权。3）相关性剪枝方法[5]：根据节点间相关性或相互作用进行剪枝，也是一种很重要的剪枝方法，最常见的做法是先判断隐节点输出之间的相关性，然后合并具有较大相关性的隐节点。

文中主要是对相关性剪枝算法进行研究，首先介绍相关性剪枝算法的思想和计算方法，然后提出新的基于误差传递的改进方案，最后通过实验建立神经网络，并对网络进行剪枝。将新的剪枝算法获得的网络与标准算法剪枝得到的网络进行对比，新算法下的网络相比于标准算法的网络的精度得到提高。

1 相关性剪枝算法

相关性剪枝算法的核心就是查找隐层节点之间的相关性，合并那些相关性比较高的节点，删除那些方差较小的节点，也就是输出值几乎为固定值的节点，并将去掉这些节点后引起的改变传递到下一层的权值连接以及输出节点的偏置值中。

1.1 相关性

相关性在剪枝过程中实际上就是隐层节点输出向量之间的线性相关性。当某两个节点之间的线性相关性大于某一标准的时候，实际上可以认为两个隐层节点的输出是线性相关的，比如说第i个节点和第j节点，存在:

而下一层第k个节点的输出：

M为隐层节点总数，vm对第m个隐层节点的输出，Ok为第k个输出节点的输出，wbk为第k个节点的偏置值。明显可以用vi代替vj，重新提取vi系数，代替wki，相应的也可以找出新的wbk。从而可以使用vi代替vj，即表示改变第i个节点与下一层节点的连接权值以及下一层节点的偏置值，就可以删除掉第j个节点。

1.2 相关性的计算

相关性算法要求先算出隐层节点的输出结果，即隐层输出数值矩阵，选取tansig作为隐层激活函数时，每个值位于[-1 1]区间上，然后算出每个隐层节点输出之间的相关度以及各节点的输出的方差。

第i个隐层节点和第j个隐层节点的相关度公式为：

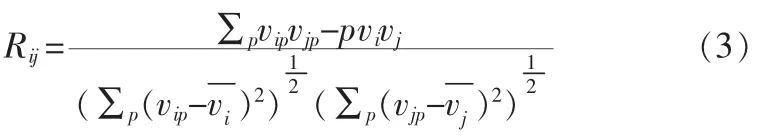
实际上就是计算向量的线性相关度的公式。

各节点的输出的方差公式如下：

其中P是隐层输出的组数，vip是第i个隐层节点的第p组输出，vi为第i个隐层节点的输出均值。

按以上公式计算后输出序列呈以下5种情况：

1）两个隐节点输出序列高度正相关；

2）两个隐节点输出序列高度负相关；

3）两个隐节点输出序列相关性不高；

4）某隐节点输出序列方差较小；

5）某隐节点输出序列方差较大。

可以处理的是线性相关度高的以及方差较小的隐层节点。

1）当两个节点线性相关度高时，对于第k个输出节点：

最后得到：

其中， a，b 的值由式（1）得：

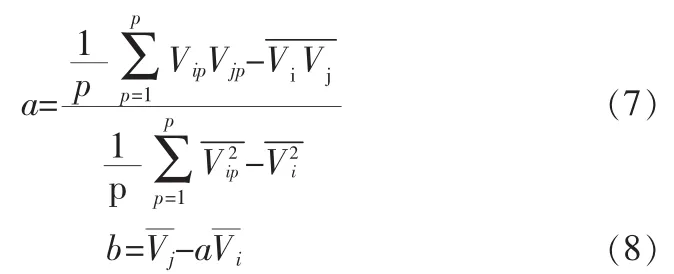
wbk为第k个输出节点的偏置值。

2）方差较小的隐层节点，可以认为输出为一个固定值，设第i个节点方差较小则直接用计算式可以得到：

综上两种方法，可以将剪枝后的相关改变传递到网络权值以及下一层的偏置值中。

但在算法中，对于Rij和取值在哪个范围才对之删除并没有明确的给出，有的材料上[5-6]，给出了:Rij＞θ1且＞θ2，＞θ2时删除两个相关节点中的一个；当＜θ2，则认为该节点的输出为固定值，可删除，其中θ1和θ2是预设的阈值，但是到底这两个值如何给出并没有给出理论依据，在网络上也搜索的类似的剪枝算法的课件，同样在θ1和θ2的取值上也没有给出明确的方法。

平生没有求过人的父亲，将给我攒好的下学期的所有费用，换成名牌酒和茶叶，趁夜色带我去校长家。父亲拖着那条在车祸中被撞瘸的右腿，走起路来很是艰难。

2 相关性剪枝算法的改进

实际计算时，由于隐层节点的方差计算完之后会有很多的方差值接近0而不等于0，选取那些接近0的方差，删除对应的隐层节点能够有效的简化网络结构，但是如何选择方差允许的上限θ2就是实际删除操作中要注意的问题。考虑到如果每次网络结果允许存在一定的误差且隐层的实际输出在这个误差允许范围内便认为其值是合理的，那么以误差传递作为基本思想，给出每个隐层节点的实际值与节点输出的均值的差，如果差值在一定的范围内则认为是合理的、没有误差的，并在计算总结所有节点误差后，删除没有误差的隐层节点。于是怎么计算由输出误差传递到隐层节点允许的误差就是至关重要的。

按照误差传递的思想，假设神经网络[7]在当前的精度下，允许误差下降率为δ，则对于第k个输出节点，如期望值为Ak，则此处允许误差为δ*Ak，相应的每个隐层节点允许的误差为 xi，则：

此时可做两种假设，如：假设每一个隐层节点的输出误差都相等，即：xi=xj，此时重新计算时：

则对于所有的输出节点，允许误差：

此处的x对所有隐层节点都是相同的。

另一种假设为：每个隐层节点的输出乘以权值后误差相等，即wkixi=wkjxj，此时重新计算时：

则对于所有的输出节点，允许误差：

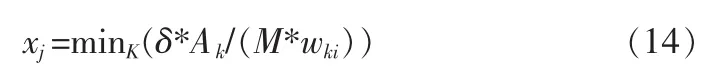
此处的xi分别对应到第i个隐层节点。

以两种方式计算的xi，即为希望求得的各节点的允许误差，那么在重新计算隐层节点输出方差时，若：

此处vi是第i个节点输出的均值。

则令vip-vi=0，计入到方差，计算公式（4）的值，这样各个节点的误差值都能求出。最后将所有方差为0的节点删除掉，并根据公式（9），计算固定值输出节点的删除下的网络变化，修正权值和偏置值，以简化网络的结构。

3 实验结果

选取数据是UCI机器学习数据中的Car Evaluation Data-base，是根据车的价格和车身配置进行选取的分类问题，将其中 1 728 个样例的 501～600，1 001～1 100，1 601～1 700 样例抽取出来作为测试样例，其余1 428个作为网络的训练样例。

网络最开始选择时，从5～40个隐层节点进行遍历，网络权值初始化全为0，偏置值全为1，找到17个隐层节点时网络的误差精度相对不错，达到0.013。而后开始使用相关性剪枝。 计算时发现[11 12]节点的方差为 0，[2，17][4，7，13][6，8]几个节点的相关性达到0.94以上。如果单独删除11，12节点，网络的误差精度不变，为 0.013；单独删除[2，17][4，7，13][6，8]中17，7，13，8节点，网络的误差精度为0.030；使用改进方法，A 设为 1，δ设为 0.01，使 xi=xj，则可删除节点还有 9，14，在删除9，11，12，14时网络的误差精度为 0.019，上升0.06，相对于以线性相关删除 17，7，13，8节点后的网络的误差0.030，新剪枝方法获得的网络性能还是不错的。

以下为5个网络的重新训练后，训练以及测试结果：net_0 原网络（未剪枝网络）；net_1 删除 9，11，12，14 节点的网络（新算法网络）；net_2 删除 7，8，13，17 节点的网络（删除线性相关节点生成的网络，此处的θ1=0.94）；net_3删除7，11，12，13，14，17 节点的网络（标准相关性算法剪枝网络，此处的 θ1=0.94，θ2=0.94）；net_4是直接以前述初始化权值训练生成的13个节点的网络，故而训练前的精度计算没有意义。

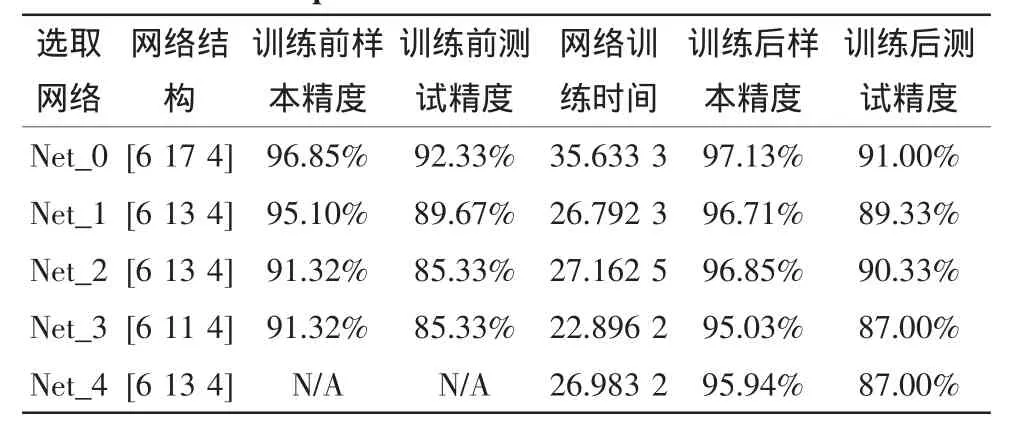
表1 5种神经网络参数对比Tab.1 Comparison of five artificial neural networks

在训练前，对比 net_0 与 net_1、net_2、net_3，新算法下的net_1相较于原网络，在减少了4个节点的情况下训练前的训练精度以及测试精度都稍微下降，但是比之删去线性相关节点的net_2，同样减少4个节点的情况下，网络的样本精度和测试精度高出近4%，足见采用新的剪切算法对于网络精度的影响要小得多。而相对于标准剪枝算法下的net_3，net_1多出两个节点，训练前的样本精度和测试精度都也要高出近4%。

训练之后，对比 net_1、net_2、net_3、net_4，样本精度和测试精度最高的是net_2，即删去相关性节点的网络，但是新算法下的net_1与之相差不大，在考虑训练样本与测试样本的选取因素下，两种方法的训练后的结果几乎相差无几。而net_1与标准算法net_3和直接生成神经网络的net_4相比，网络无论是样本精度还是测试精度都要高出3-4%，存在较大优势。

时间消耗上，对比可见，网络隐层节点数越多，训练的时间开销越大。而在同样多隐层节点数的几个网络中，net_1的时间消耗最少，当然因为机器运行时的实际情况不同，也会对网络的时间开销有影响，此条仅参考。

综上实验对比，新算法在神经网络直接剪枝后，无论是样本精度还是测试精度都高于其它的基于相关性剪枝算法所获得的精度，剪枝效果明显不错。重新对网进行训练后，网络的样本精度和测试精度略低于删去线性相关节点的网络，但是相差不大。而比之标准相关性网络和直接训练13个节点的网络，精度要高得多。训练时间开销上，新算法生成的网络略少。

4 结 论

文中关于相关性算法的改进是研究神经网络知识规则提取方法过程中发现的问题并进行研究和改进。首先通过不断增长隐层节点的方法选取节点数，而后通过相关性算法和改进算法对网络进行了剪枝，以达到简化网络结构的目的。实验表明新算法的网络剪枝方面不仅能够尽量减少节点数，还能保证对网络精度影响较小，对比于其他方法下的网络有一定的优势。目前给出的方法思路和计算相对简单，许多地方有待改进，今后将进一步对之进行研究。

[1]Reed R.Pruning algorithms-a survey[J].IEEE Trans Neural Networks，1993，4（5）:740-747.

[2]周志华，陈世福.神经网络规则抽取[J].计算机研究与发展，2002:39（4）:398-405.

ZHOU Zhi-hua，CHEN Shi-fu.Rule extraction from neural networks[J].Journal of Computer Research and Development，2002，39（4）:398-405.

[3]雷素娟.一种改进的RBF神经网络及其在股市中的应用[D].泉州：华侨大学，2009.

[4]朱万富.基于粗集神经网络的故障诊断专家系统研究[D].青岛：中国石油大学（华东），2007.

[5]宋清昆，郝敏.基于改进相关性剪枝算法的B P神经网络的结构优化[J].控制理论与应用，2006，25（12）:4-6

SONG Qing-kun，HE Min.Structural optimization of BP neural network based on correlation pruning algorithm[J].Control Theory and Applications， 2006， 25（12）:4-6.

[6]赵寿玲.BP神经网络结构优化方法的研究与应用[D].苏州：苏州大学，2010.

[7]杜双育，袁红波，王先培.基于BP神经网络和气象统计的绝缘子污闪预警研究[J].陕西电力，2012（11）：8-11，33.

DU Shuang-yu，YUAN Hong-bo，WANG Xian-pei.Early warning of insulator pollution flashover based on BP Network and meteorological statistics[J].Shaanxi Electric Power，2012（11）：8-11，33.