载波相位平滑伪距算法研究与精度分析

隋叶叶，杨小江，柳 涛

（航天恒星科技有限公司 北京 100086）

伪距定位法是指利用伪距及广播星历的卫星轨道参数和卫星钟差改正进行的定位。由于卫星时钟误差一般为3 m左右，均方差约为2 m，伪距观测噪声为30 cm，广播星历的轨道精度为m级，卫星钟差的改正精度为几十纳秒，因此在高动态条件下，单点定位的坐标分量精度通常在10 m左右。而结合伪距确定周整模糊度的非差精密单点定位的精度可达2 cm[1-5]，但是由于载波相位存在周整模糊度问题，因此实现较为复杂。而载波相位平滑伪距将伪距无周整模糊度与载波相位观测量高精度的特点相结合进行单点定位，能够有效提高伪距精度，且实现方法简单，更加适合在空间飞行器上使用。

文中提出一种基于载波差量进行周跳探测的方法，根据卫星、飞船的轨道特点，选择合理的伪距/平滑伪距解算切换策略与周跳处理方式，并对参数的确定进行仿真分析，解算出航天器的位置信息。该方法实现简单，并能够可靠地检测周跳，保证定位结果的平滑并有效提高定位精度。

1 定位精度影响因素分析

由GPS确定的位置、时间解的精度最终表示为几何因子和伪距误差因子之积。粗略地讲，GPS解的误差用下式来估计[6]：

（GPS解的误差）=（几何因子）×（伪距误差因子）在适当的假设条件下，伪距误差因子就是伪距值的实际精度。而几何因子表示卫星/用户的相对几何布局对GPS解的误差的复合影响，一般地，将它称做与卫星/用户几何布局相关联的几何精度因子。

GPS标准定位服务的伪距误差（m）估算表如表1[6]所示。

由表1可以看出，伪距误差一般在7 m左右，在单点定位误差中占有很大比重。采用载波相位平滑伪距的方法，可以消除伪距噪声，改进伪距误差，从而有效地提高单点定位精度。因此，文章对载波相位平滑伪距算法进行研究，并对高动态环境下算法的适用性进行分析。

表1 伪距误差源Tab.1 Sources of pseudorange error

2 载波相位平滑伪距原理

目前GPS接收机实时导航解采用的大多是伪距定位。但伪距观测值由于其本身的精度比较低，如果直接带入单点定位的观测方程中进行求解的话也会降低定位结果的精度，所以一般不用来直接进行求解。虽然载波相位测量的精度比伪距测量的精度高两个数量级，但载波相位周整模糊度无法直接测得，所以也难以直接利用载波观测值。如果能用载波相位观测值对伪距观测值进行修正的话，就可以提高伪距定位的精度。这就是所谓的相位平滑伪距。

载波相位平滑伪距的方法是利用高精度的载波相位观测值改善伪距观测值的精度。在忽略观测误差的条件下，其数学模型中所表示的伪距与载波相位观测值之间的关系如下：

其中：ρ为伪距，φ为载波相位，N为初始周整模糊度，λ为载波波长。

观测过程中若不存在周跳，则N保持不变，接收机自动对载波相位φ连续计数。设接收机对某颗导航星连续跟踪n个历元，有则可得周整模糊度近似为采用递推算法，n+1时刻的平滑伪距为

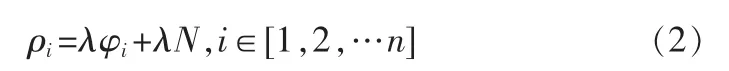
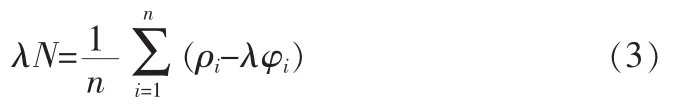
3 载波相位平滑伪距单点定位软件设计

由于GPS导航星座的变化、障碍物的遮挡、接收机的运动、较低信噪比及接收机故障，导航定位过程中，可见星的变化与周跳现象时有发生。在载波相位平滑处理中，如何对这些特殊情况进行处理将直接影响到平滑的效果及定位精度。

载波相位与码伪距观测量之间有如下关系[7]：

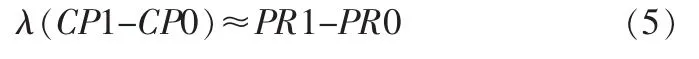
其中λ为载波波长；CP1、CP0分别为k+1、k时刻的载波观测量，单位为周；PR1、PR0分别为k+1、k时刻的伪距观测量。

基于此，可以采用如下的周跳处理方式：令

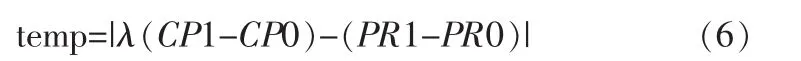
该量体现了相邻两个历元间的载波观测量的连续性，称为载波差量。将该量做为k+1时刻是否发生周跳的判决依据。

在该平滑算法中，设定周跳判断门限，对于载波差量超出此判决门限的历元，认为该时刻发生周跳。若一颗星连续发生周跳的次数很小，则认为之前的平滑数据仍然有效，跨越该时刻继续平滑；否则，历史数据无效，对平滑器进行重置，使用该时刻的伪距测量值ρ1来初始化即

反之，若载波差量在周跳判决门限之内，则按没有周跳进行处理。且载波差量越小，说明载波的连续性越理想，此时刻的平滑伪距较伪距原始观测量越可信。因此设定一个小门限，对于载波差量在小门限之内的卫星，选择平滑后的伪距参与解算；否则，平滑伪距仅保存而不做解算。

另外，伪距平滑窗口也应该合理取值。滑动窗口太大，则当前时刻的伪距观测量在平滑伪距中占很小的权重，因此考虑到相位误差的累计变化，可能导致定位结果的发散；滑动窗口过小，则载波相位对平滑伪距的贡献也相应减小，从而对平滑效果造成影响。

4 算例分析

根据GPS载波相位平滑伪距的原理，就是以小尺度的相位观测值平滑大尺度的码伪距观测值，以达到提高精度的作用。因此，与信号传播有关（对流层折射、电离层折射、相对论效应及多路径效应）的误差项，都以载波相位观测值所达到的精度为平滑伪距精度；平滑过程的改正量又是第i与i-1次相位观测值的差分过程，使得与接收机、测站和卫星有关的相近误差得以削弱或抵消，从而达到平滑伪距较C/A码伪距精度得以改善的目的。

为更加有效地验证算法在实际应用中的特性，测试数据选用周跳、变星次数较多的动态数据。

4.1 实验条件

算例数据采用2012年2月1日的高动态实测数据。数据提供CA码及L1载波相位测量值，采样间隔为1 s，观测历元取3 600 s。导航文件采用IGS提供的该天的广播星历，星历每2小时更新一次。以事后处理所得的精密定轨数据作为基准值。伪距平滑后的计算结果与基准值进行分析比较，得出分析结果。

4.1.1 数据特性

各历元的可视星数目与PDOP值、定位误差（单位为m）曲线图分别如图1、2。

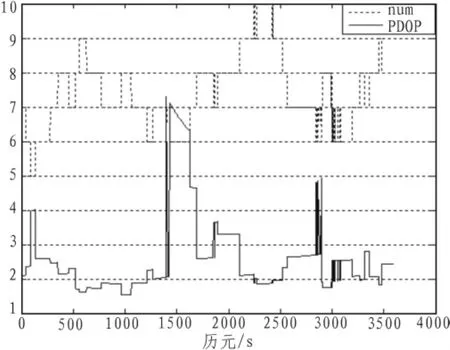
图1 可视卫星数与PDOPFig.1 Satellite numbers and PDOP

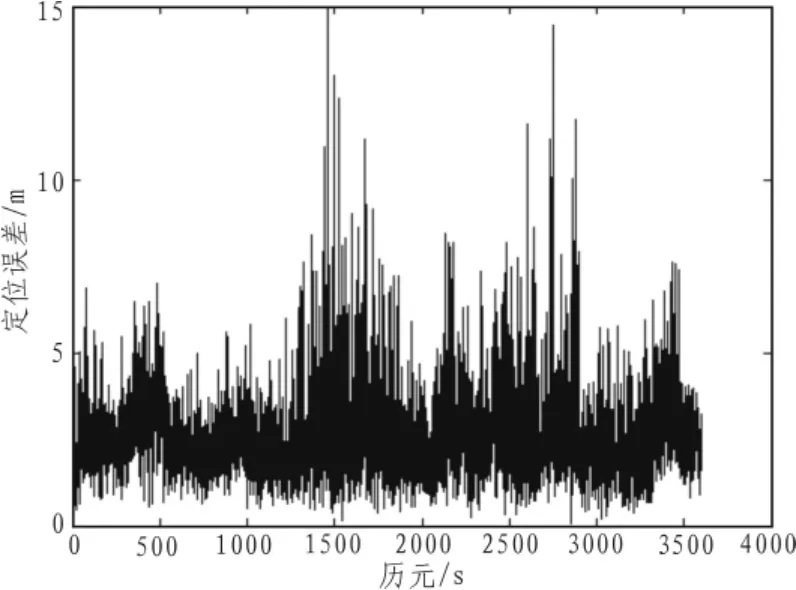
图2 定位误差曲线Fig.2 Positioning error plot

为了更加清晰地对比PDOP与定位结果的变化关系，将前200历元时刻两者的变化曲线放大如图3。

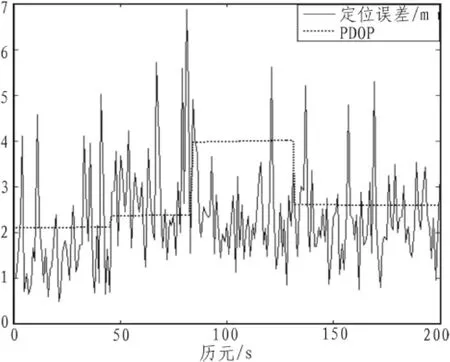
图3 PDOP与定位误差的对比Fig.3 The comparison of PDOP and positioning error

由图3可以看出，定位误差曲线并不随着PDOP曲线的变化而变化。即使在PDOP值不变的情况，定位误差也有可能出现较大抖动。说明在该测量数据作为输入时，卫星的几何分布对定位精度几乎不产生影响[8]，定位精度的变化主要是受新上/下星的伪距精度的影响。因此，如何处理新上/下星，对定位精度将产生直接的影响。

4.1.2 参数取值确定

该平滑技术虽然能够简单有效地实现周跳检测及伪距平滑，但是平滑参数的选择需要适应不同的应用环境。本节针对在该组原始数据条件下，周跳判断门限和伪距平滑窗口的取值进行分析确定。

伪距平滑窗口取适中值400时，不同的周跳门限取值对定位结果的影响如表2所示。

表2 周跳门限取值分析Tab.2 Cycle slip threshold value analysis

周跳门限过大，容易漏判，从而引入误差较大的点做平滑，使得平滑结果整体偏离；周跳门限过小，容易误判，从而载波相位得不到充分的利用，影响平滑效果。由上表2可以看出，在周跳门限大于15时，定位结果不再随它的变化而改变。周跳门限为10时，定位误差均方差接近最小值。

在周跳门限取值确定的基础上，表3显示了平滑窗口对定位精度的影响。

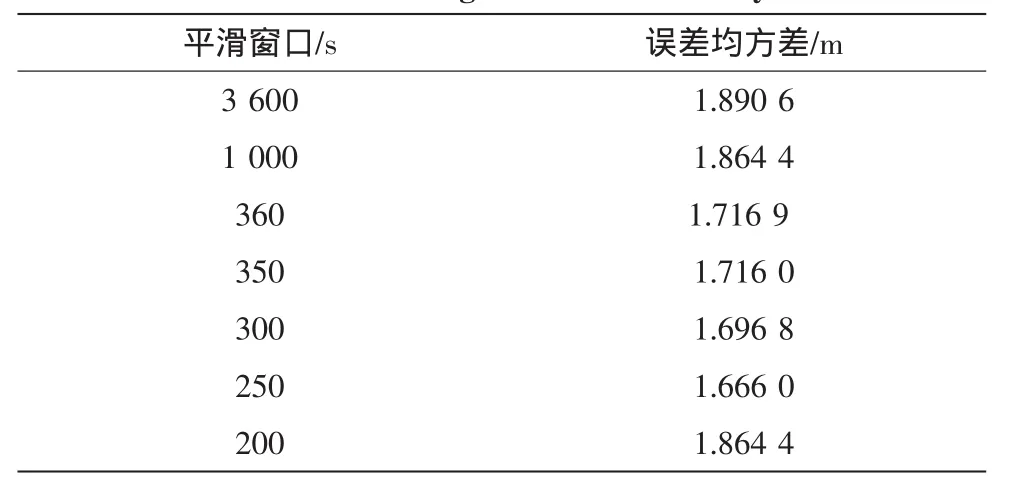
表3 平滑窗口取值分析Tab.3 Smoothing window value analysis

由上表可以看出，在平滑窗口为250时误差均方差达到最小值，所以在该算例分析中，平滑窗口大小取250合适。

4.2 定位精度分析

当伪距未被载波相位平滑时，单点定位的三轴分量偏差如图4。

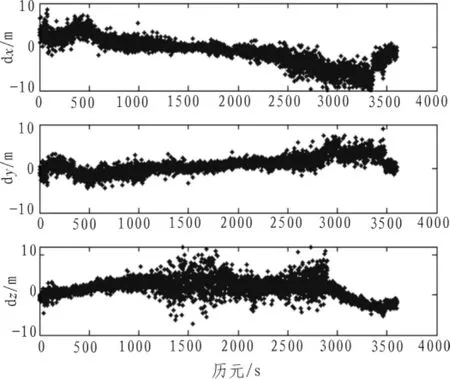
图4 C/A码定位三轴分量偏差Fig.4 Three-axis component deviation of C/A code positioning

图4中，定位误差的随机噪声较大，误差范围在±10 m以内，误差的均方差为2.3 m。伪距采用载波平滑之后，单点定位的三轴分量偏差如图5。

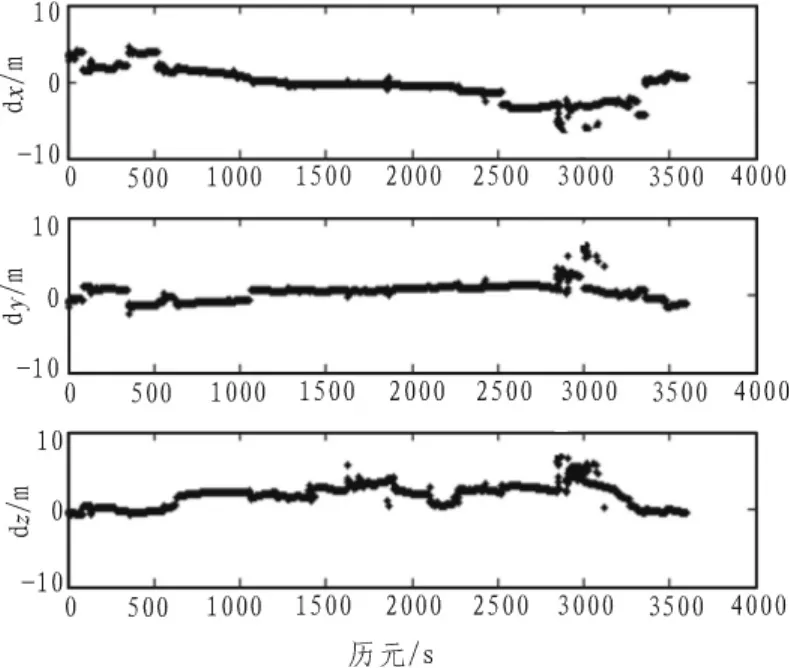
图5 C/A码平滑伪距定位三轴分量偏差Fig.5 Three-axis component deviation of smoothing code pseudorange positioning

对比图4、图5可以看出，图5中定位精度有明显改善，随机噪声明显减小，且定位误差在±5 m以内，误差的均方差为1.7 m。

4.3 平滑伪距相关分析

为了从统计意义上分析平滑的效果，选取没有周跳的一段数据进行分析。以十四号星为例，取一段十分钟的无周跳数据进行仿真分析。

如图 6，图（a）、（b）、（c）分别显示伪距与载波差量、平滑伪距与载波差量、平滑伪距与伪距差量曲线。其中，为了更加便于图形的分析，图a、b显示的均是消去均值之后的效果。

图6 十四号星相关差量曲线Fig.6 Related differential curve of 14th star

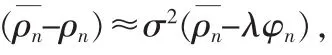
另外，σ2（-λφn）比 σ2（ρn-λφn）小很多，说明平滑后的伪距偏差很小，且平滑后的伪距更趋近于载波相位观测量，这也证明了平滑的有效性。

5 结 论

通过对以上测试数据分析可以看出，在高动态条件下，伪距定位法的定位精度为10 m。而通过载波相位平滑伪距处理之后，定位精度明显提高，定位误差在5 m之内。从统计结果也可以看出，平滑之后的伪距精度更加趋近于载波精度，该平滑方法在高动态环境下具有良好的平滑效果。文章还确定了在该高动态环境下，平滑窗口、周跳门限的合理取值，为高动态环境平滑伪距技术应用时参数的确定提供了参考。

[1]吴江飞，黄城.GPS精密单点定位模型及其应用分析[J].大地测量与地球动力学，2008，28（1）:96-100.

WU Jiang-fei，HUANG Cheng.GPS precise point positioning models and the utility analysis[J].Journal of Geodesy and Geodynamics，2008，28（1）:96-100.

[2]郝明，丁希杰.GPS精密单点定位的数据处理方法综述[J].测绘工程，2008，17（4）:60-62.

HAO Ming，DING Xi-jie.Study of data processing methods for GPS precise point positioning[J].Engineering of Surveying and Mapping，2008，17（4）:60-62.

[3]Gao Y.Development of a real-time single-frequency precise point positioning system and test results[C]//Pro-ceedings of ION GNSS 2006，Fort Worth，TX，2006：26-29.

[4]Hyumho R，et ai.Dual-frequency GPS precise point positioning with WADGPS corrections[C]//Proceedings of ION GNSS 2005，LongBeach，CA，September，2005：13-16.

[5]唐卫明，刘智敏.GPS载波相位乎滑伪距精度分析与应用探讨[J].测绘信息与工程，2005，30（3）:37-39.

TANG Wei-ming，LIU Zhi-min.Precision evaluating and applications of GPS code pseudorange smoothing algorithm based on carrier observables[J].Journal of Geomatics，2005，30（3）:37-39.

[6]Kaplan E D，Hegarty C J.Understanding GPS:principles and applications，second edition[M].Normood，MA:Artech House，2006.

[7]谢钢.GPS原理与接收机设计[M].北京:电子工业出版社，2009.

[8]徐峰，张少博，陈海峰.发动机热试车数据测量误差分析及处理方法[J].火箭推进，2012（4）：72-75.

XU Feng，ZHANG Shao-bo，CHEN Hai-feng.Error analysis and processing of engine hot test data[J].Journal of Rocket Propulsion，2012（4）：72-75.