基于符号化部分互信息熵的多参数生物电信号的耦合分析*

张梅 崔超 马千里 干宗良† 王俊‡

1 引言

近年来,心脑血管等身体内部器官疾病的发病率不断地增加,为了对身体内部器官的健康状况进行准确的预报和诊断,需要行之有效的方法来采集和分析人体生物电信号.目前生物电信号采集和记录技术有了很大进步.相比较于生物电信号采集技术的突飞猛进,生物电信号的分析技术的进展[1-4]却不尽如人意.目前常用的生物电分析方法主要有时域分析[5-11]、频域分析[6-9,12]、功率谱分析[13,14]、神经网络[12,15-19]分析方法等,但大多数是停留在理论方面,没有广泛地应用于实践.

本文提出了一种新的生物电信号分析方法——基于符号化部分互信息的多参数生物电信号的分析方法,这种方法用于分析生物电信号之间的耦合信息.分析两个或两个以上系统的耦合关系十分有益,以分析生物电信号为例,由于目前尚不能完全掌握这些系统,所以我们的分析局限于已记录的生物电信号上.部分互信息可以反映这些信号间的相关性,这对于疾病的检测和诊断具有重要意义.

如果直接对生物电信号原始序列进行部分互信息分析[20],由于噪声等因素的影响,往往不能准确地对信号序列进行分析.而且和其他基于熵的算法一样,基于部分互信息的耦合分析方法也存在不足,要求数据量较大,而且时间序列具有很好的平稳性,这些都给实际应用带来困难.

针对以上问题,本文提出了使用符号化的部分互信息来对生物电信号进行耦合分析.符号化[21,22]是动力学系统研究的一个重要手段,其主要的意义是对噪声的影响不敏感,得到的结论较为严格,而其应用的关键在于如何划分符号区域,使得处理后的信号不会丢失时间序列的动力学特性.

2 基本原理

对于一个离散随机变量X,有概率分布{px},其信息熵定义如下：

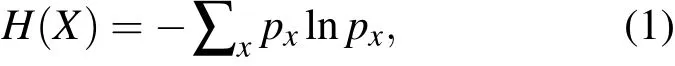
两个随机变量X和Y的互信息定义为

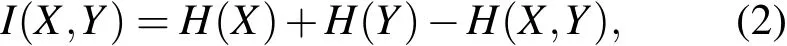
I(X,Y)反映了随机变量X和Y间的相关性,其中联合熵H(X,Y)由XY的联合分布{pxy}计算得到.

部分互信息I(X,Y|Z)是XY相交但不包括Z的部分,其定义式如下：

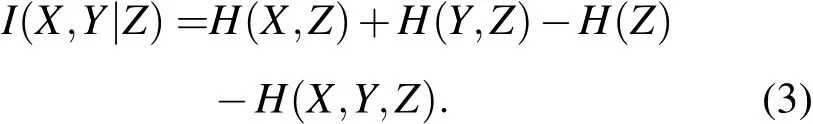
I(X,Y|Z)表示在已知Z的情况下Y提供的关于X的平均信息量,其物理意义如图1所示.

图1 部分互信息I(X,Y|Z)(间断条纹部分)

对于相同的Z部分信息熵是对称的,即I(X,Y|Z)=I(Y,X|Z),同样有0≤I(X,Y|Z),当且仅当XY相互独立时取零,特别是当X或Y是Z的函数时.随机变量间的互信息越大,其耦合程度越大.

为了克服噪声等因素的影响,本文提出了使用符号化的部分互信息来对生物电信号进行耦合分析.原始序列的符号化定义如下[23,24]：

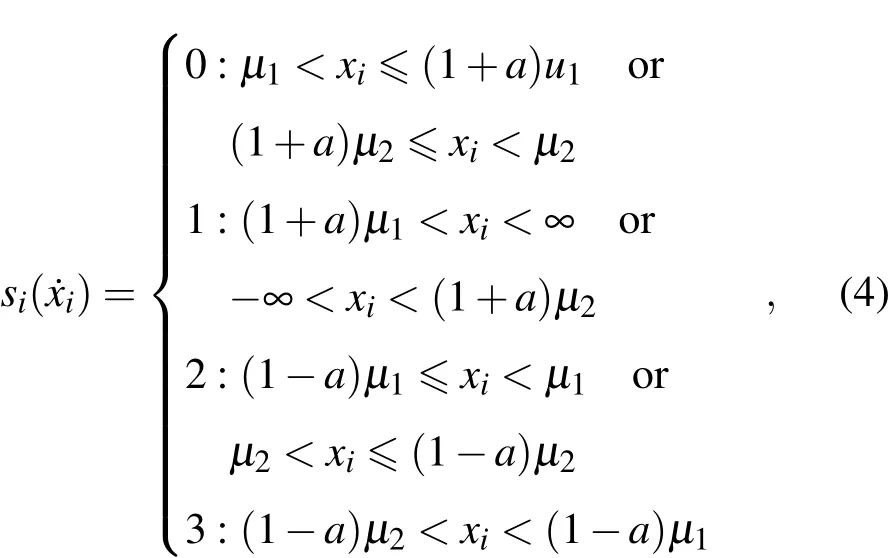
其中µ1是原始序列中大于等于零的取样信号的平均值,µ2是小于零的平均值,取a=0.05.符号化主要的意义是对噪声的影响不敏感,得到的结论较为严格,而其应用的关键在于如何划分符号区域,使得处理后的信号不会丢失时间序列的动力学特性.当a取0.04到0.07时都可得到原信号的大尺度信息,如果a取小于0.04或大于0.07时,会得不到较为合理的统计特性.这是因为在符号化的过程中,如果a的值过大或过小,会导致细节信息的丢失.故取a=0.05,既能去掉原信号噪声影响,又能较好地捕捉信号中的动态信息.

为了取得更好的分析效果,本文将原始序列符号化与部分互信息分析法结合,即先对多参数的生物电原始信号脑电X,心电Y,肌电Z进行符号化及编码处理,得到符号化序列˙X,˙Y,˙Z,再计算其部分互信息来获得多参量生物电信号的耦合信息,符号化的部分互信息定义如下：

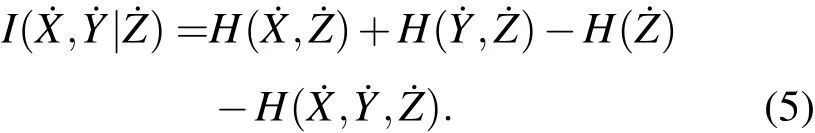
3 基于符号化部分互信息的生物电信号耦合分析

3.1 实验数据

本文使用的睡眠数据来自PhysioBank的MITBIH Polysomnographic Database.该库中的记录是多参数睡眠数据,包括1导EEG(electroencephalogram)信号,1导ECG(electrocardiosignal)信号,1导EOG(eyectro-oculogram)信号,1导EMG(electromyographic signal)信号等多导睡眠信号,记录长度为6 h,数据采样频率250 Hz,每份记录的数据都附带着以30 s为一个分期的注释信息,本文的实验结论判定依此注释为参考.

本文所用数据,分别采用了15组受试者睡眠和清醒期的多参数生物电信号数据中的1导EEG(C3-O1)脑电信号、1导ECG心电信号、1导EMG肌电信号,提取其中的清醒期和NREM睡眠I期的若干组信号,分别记为样本Sleep和Weak.

3.2 实验方法

根据本文提出的算法,我们首先根据(4)式对生物电原始信号各参量EEG,ECG,EMG进行相应的符号化及编码处理,再根据(5)式计算生物电信号样本Sleep和Weak各参量间的部分互信息I(EEG,ECG|EMG),从而分别获得睡眠期和清醒期生物电信号的耦合信息.最后使用spss统计分析软件对计算结果进行了假设检验,验证了该算法的有效性.以生物电信号的耦合信息作为参数,我们可以判断该生物机制是处在活跃的还是消极的状态,这对于一些身体内部器官健康状况的诊断具有重要意义.

3.3 实验结果及分析

3.3.1 研究多参量生物电信号耦合程度与数据长度L的关系

对受训者样本15组Sleep和15组Wake中的每组生物电信号序列分别取数据长度L=500,1000,1500,2000,2500,3000,并对每个时间序列进行符号化及编码处理,分别计算每个个体的部分互信息,并分别对睡眠期部分互信息和清醒期部分互信息进行平均,得到部分互信息与数据长度L的关系如图2所示.

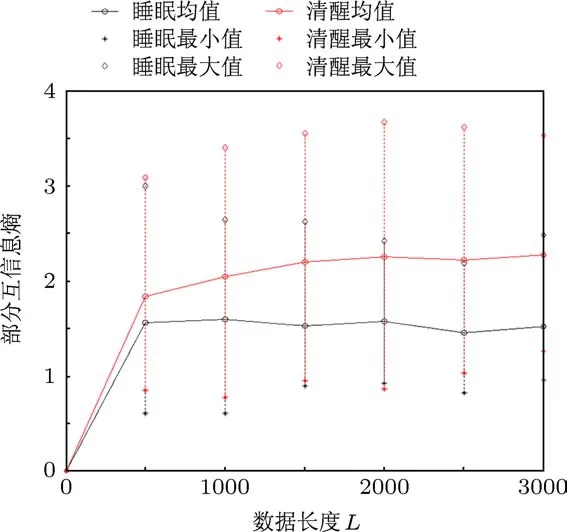
图2 部分互信息熵与数据长度L的关系

分析图2睡眠期与清醒期的部分互信息曲线可知：

1)在数据长度相等的情况下,清醒期的生物电信号耦合程度要高于睡眠期;

2)当数据长度由0增至2000的过程中,睡眠期与清醒期的耦合程度分别呈递增趋势,数据长度大于2000时,耦合程度趋于平稳,基本不变.

从数据的精准性考虑,数据长度越大,其统计概率分布越接近实际分布,相应的准确性越高.但从计算量以及计算速度来讲,数据长度越小,那么算法速度也越快,综合我们的实验结果,取数据长度L=2000时,既能兼顾处理速度,又可以保证实验精度.

3.3.2 研究多参量生物电信号耦合程度与编码长度N的关系

对受训者样本15组Sleep和15组Weak中的每组生物电信号序列分别取编码长度N=1,2,3,4,5,6,并对每个时间序列进行符号化及编码处理,分别计算每个个体的部分互信息,并分别对睡眠期部分互信息和清醒期部分互信息进行平均,得到生物电信号耦合程度与编码长度N的关系如图3所示.

图3 部分互信息熵与编码长度N的关系

分析图3部分互信息与编码长度N的关系可知：

1)在编码长度N从1到6的递增过程中,生物电信号的部分互信息都成增大趋势;

2)清醒期的耦合程度明显高于睡眠期的,且在N=6时清醒期与睡眠期耦合程度差异最显著.

考虑到实验效果的明显性,N应该取大些;考虑到算法的复杂度会影响实验处理速度以及在临床应用上的实时性,N应该取小一些.综合考虑上述因素,N取6.

3.3.3 研究在数据长度L=2000,编码长度N=8条件下青老年能量耗散的差异

对受训者样本15组Sleep和15组Weak中的每组生物电信号序列分别取编码长度N=6及数据长度L=2000,计算每个个体的部分互信息,得到生物电耦合程度与睡眠期清醒期的关系如图4所示.

分析图4睡眠期与清醒期的生物电信号耦合程度对比可知：

1)清醒期生物电信号耦合程度明显高于睡眠期的,生物电信号的部分互信息熵可以作为衡量一个过程是否处于积极有序状态的参数,耦合程度越高,说明该物理过程越有序;

2)上图中0—14号生物电信号个体间的生物电信号耦合程度有很大差异,不同个体处于不同的年龄段和具有不同的体重引起的.

3.3.4 统计分析与假设检验

为进一步验证本文计算结果的准确性及算法的有效性,使用spss统计分析软件对计算结果进行了假设检验,主要方法如下.

对清醒期与睡眠期生物电信号耦合程度的差异显著性进行假设检验,分别将睡眠期和清醒期的部分互信息值记作样本S和W,使用spss对两组部分互信息数据S,W进行独立样本T检验,结果如表1所示.

图4 睡眠期与清醒期的生物电信号耦合程度对比

表1 清醒期与睡眠期生物电信号耦合程度的差异显著性假设检验

本文关注的是准确地对清醒期与睡眠期生物电信号进行判断和辨别,根据表1分析清醒期与睡眠期生物电信号耦合程度的差异显著性,假设清醒期与睡眠期的均值相等：

1)由表1可知,在假设方差相等的情况下,自由度(d f)为28,查找t值表可知理论t值t(d f)0.05=t(28)=2.048,而样本t值为3.291,大于t(28),且Sig(双侧)=0.003＜0.05,假设不成立,所以清醒期与睡眠期生物电信号耦合程度差异显著;

2)由表1可知,在假设方差不相等的情况下,自由度(d f)为23,查找t值表可知理论t值t(d f)0.05=t(23)=2.069,而样本t值为3.291,大于t(23),且Sig(双侧)=0.003＜0.05,假设不成立,所以清醒期与睡眠期生物电信号耦合程度差异显著,证明该算法可以有效地对清醒期与睡眠期生物电信号进行区分.

以上实验结果证明,使用符号化的部分互信息算法可以很好地对多参数生物电信号的耦合程度进行分析,以生物电信号各参量之间的耦合程度作为参数,能够有效地辨别该生理机制是否是活跃的,这对于身体内部器官健康状况的诊断具有重要意义.

4 结束语

1)提出了一种新的部分互信息的计算方法——符号化部分互信息,经验证该算法能够很好地分析离散随机变量间的耦合信息.

2)使用符号化的部分互信息来计算生物电时间序列间的耦合程度,实现了利用统计学来量化研究生命现象.

3)基于该算法分别对睡眠期和清醒期的EEG,ECG,EMG多参量生物电信号进行分析.分析结果表明,清醒期的生物电信号的耦合程度显著高于睡眠期的.并进行了假设验证,证明睡眠期和清醒期的生物电耦合信息具有显著差异,表明耦合程度可以作为衡量一个物理过程是否处于积极状态以及睡眠分期的参数.

[1]Fang X L,Jiang Z L 2007 Acta Phys.Sin.56 7330(in Chinese)[方小玲,姜宗来2007物理学报56 7330]

[2]Meng Q F,Zhou W D,Chen Y H,Peng Y H 2010 Acta Phys.Sin.59 123(in Chinese)[孟庆芳,周卫东,陈月辉,彭玉华2010物理学报59 123]

[3]Ma Q L,Bian C H,Wang J 2010 Acta Phys.Sin.59 4480(in Chinese)[马千里,卞春华,王俊2010物理学报59 4480]

[4]Bian H R,Wang J,Han C X,Deng B,Wei X L,Che Y Q 2011 Acta Phys.Sin.60 118701(in Chinese)[边洪瑞,王江,韩春晓,邓斌,魏熙乐,车艳秋2011物理学报60 118701]

[5]Wang J,Ma Q L 2008 Chin.Phys.B 17 4424

[6]Hsu W Y 2012 Int.J.Neural Syst.22 51

[7]Nevado-Holgado A J,Marten F,Richardson M P,Terry J R 2012 Neuro Image 59 2374

[8]Petrantonakis P C,Hadjileontiadis L J 2012 IEEE Trans.Signal Proces.60 2604

[9]Thatcher R W 2012 Dev.Neuropsychol.37 476

[10]Wang J,Yu Z F 2012 Chin.Phys.B 21 018702

[11]Wang J,Zhao D Q 2012 Chin.Phys.B 21 028703

[12]Musselman M,Djurdjanovic D 2012 Exp.Syst.Appl.39 11413

[13]Shao S Y,Shen K Q,Yu K,Wilder-Smith E P V,Li X P 2012 Clin.Neurophysiol.123 2042

[14]Tarokh L,van Reen E,Acebo C,Le Bourgeois M,Seifer R,Fallone G,Carskadon M A 2012 Alcohol.-Clin.Exp.Res.36 1530

[15]Wang R F,Zhang J H,Zhang Y,Wang X Y 2012 Biomed.Signal Proc.Control 7 490

[16]Orhan U,Hekim M,Ozer M 2012 J.Med.Syst.36 2219

[17]Acharya U R,Sree S V,Alvin A P C,Suri J S 2012 Exp.Syst.Appl.39 9072

[18]Siuly S,Li Y 2012 IEEE Trans.Neur.Syst.Reh.Eng.20 526

[19]Acharya U R,Molinari F,Sree S V,Chattopadhyay S,Ng K H,Suri J S 2012 Biomed.Signal Proc.Control.7 401

[20]Frenzel S,Pompe B 2007 Phys.Rev.Lett.99 204101

[21]Staniek M,Lehnertz K 2008 Phys.Rev.Lett.100 158101

[22]Li J,Ning X B 2006 Phys.Rev.E 73 052902

[23]Wessel N,Ziehmann C,Kurths J,Meyerfeldt U,Schirdewan A,Voss A 2000 Phys.Rev.E 61 733

[24]Shen W,Wang J 2011 Acta Phys.Sin.60 118702(in Chinese)[沈韡,王俊2011物理学报60 118702]