带两个形状参数的四次Bézier曲线的扩展

刘小琼， 杨国英

（河南理工大学数学与信息科学学院，河南 焦作 454000）

带两个形状参数的四次Bézier曲线的扩展

刘小琼， 杨国英

（河南理工大学数学与信息科学学院，河南 焦作 454000）

给出了两组带两个形状参数λ, μ 的六次多项式基函数，它们是四次Bernstein基函数的扩展。分析了这两组基函数的性质，基于这两组基分别定义了带形状参数的两类多项式曲线，两类曲线具有与四次 Bézier曲线类似的性质，且在控制顶点不变的情况下，可通过改变形状参数的值实现对曲线形状的调整。参数λ, μ具有明显的几何意义。当λ=μ=0时，均退化为四次Bézier曲线。实例表明，论文所采用的方法控制灵活，方便有效。

曲线设计；四次Bézier曲线；形状参数

用 Bernstein基函数表示相应用控制顶点定义的Bézier曲线是一种独特的参数多项式曲线。它不仅具有优良的控制性质，而且几何直观，结构简单，是计算机辅助几何设计(CAGD)中表示曲线和曲面的重要工具之一[1]。然而Bézier方法也有一定的缺陷，它不具备局部修改性质，即给定了控制顶点及相应的 Bernstein基函数以后，Bézier曲线也就惟一确定了。若要修改曲线的形状，必须要调整控制顶点。为了弥补这一缺陷，人们开始想办法推广Bézier曲线。

在文献[2]中，讨论了一类可调控的Bézier曲线，针对n+1个控制顶点，用m=l(n- 1 )+1次Bernstein基构造了一类 Bézier曲线。文献[3-5]分别给出了二次、三次、四次Bézier曲线的扩展。文献[6]在文献[2]的基础上给出n次Bernstein基函数的扩展，由此定义了一个带形状参数λ的n+1次Bézier曲线。

这里给出了四次 Bézier基函数的另 2类扩展，通过引入2个形状参数，将四次Bézier基函数的次数提高了2次，得到2组带有形状参数λ,μ的基函数，由2组基函数分别构造了2类曲线，相应称为第1类六次λμ-Bézier曲线和第2类六次λμ-Bézier曲线。它们具有与四次 Bézier曲线类似的性质。在控制顶点不变的情况下，随着参数λ,μ的改变可产生两类逼近控制多边形的不同曲线，且形状参数具有明确的几何意义。运用张量积方法，可生成与曲线性质类似的形状可调的曲面。用这种方法可以设计出丰富的曲线形状，满足实际应用中不同的需求。

1 第1类曲线的定义及性质

定义1 对于t∈ [ 0 ,1]，称关于t的多项式

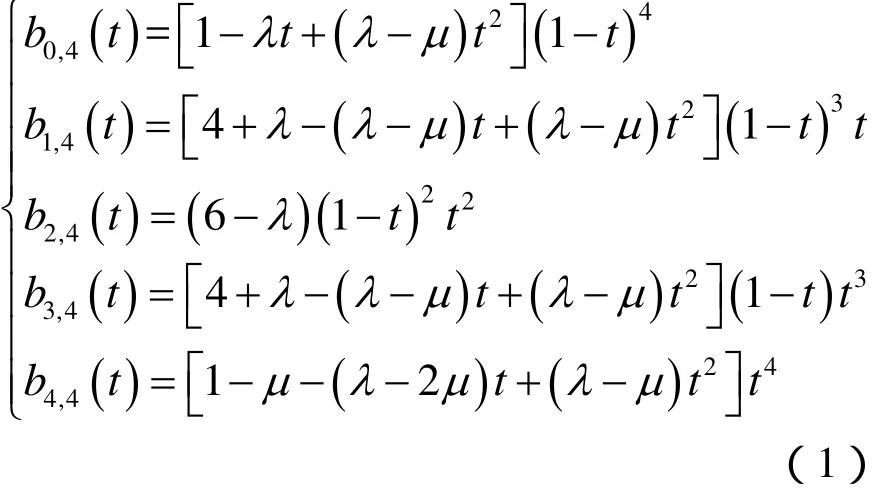
为带形状参数,λ μ的第1类基函数，简称为第1类λμ-B基。其中，当λ=μ时，-4≤λ,μ≤1；当λ≠μ时，-2≤λ≤2，-2≤μ≤1。下面的图1给出了λ=-1，μ=0时的第1类基函数图形。

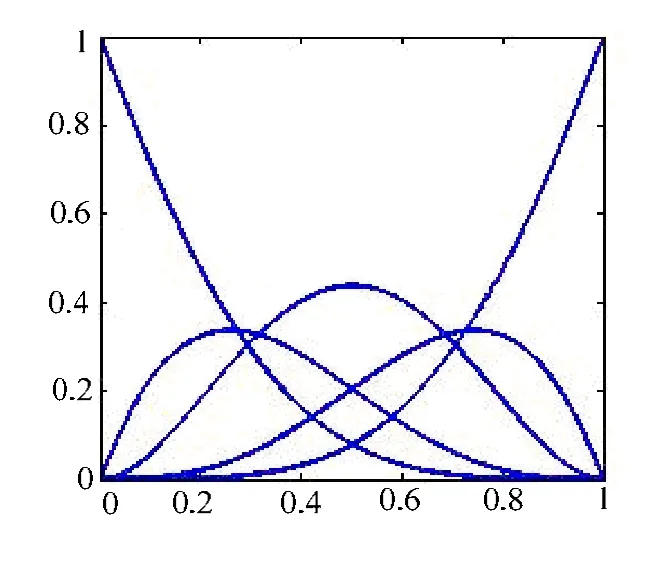
图1 λ =-1， μ=0时的第1类基函数

第1类基函数具有以下性质：

性质5 退化性 当==0λ μ时，式(1)退化为四次Bernstein基，当=0λ μ≠时，式(1)退化为文献[5]中的第2类λ-B基。此性质说明，式(1)是四次Bernstein基的扩展。称式(2)所定义的曲线为带有形状参数,λ μ的第1类六次 Bézier曲线，简称为第 1类六次λμ-Bézier曲线。显然当==0λ μ时，第1类六次λμ-Bézier曲线退化为四次Bézier曲线。

由第 1类基函数的性质可得曲线(2)具有以下性质：

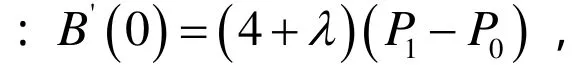
性质 2 凸包性 由基函数的非负性和规范性知曲线是落在其控制顶点生成的凸包之内。

性质 4 几何不变性和仿射不变性 曲线仅依赖于控制顶点而与坐标系的选择无关。曲线作仿射变换，只需将其控制多边形作仿射变换。

性质 5 变差减少性质(V.D.)。

2 第2类曲线的定义及性质

定义3 对于t∈ [ 0 ,1]，称关于t的多项式

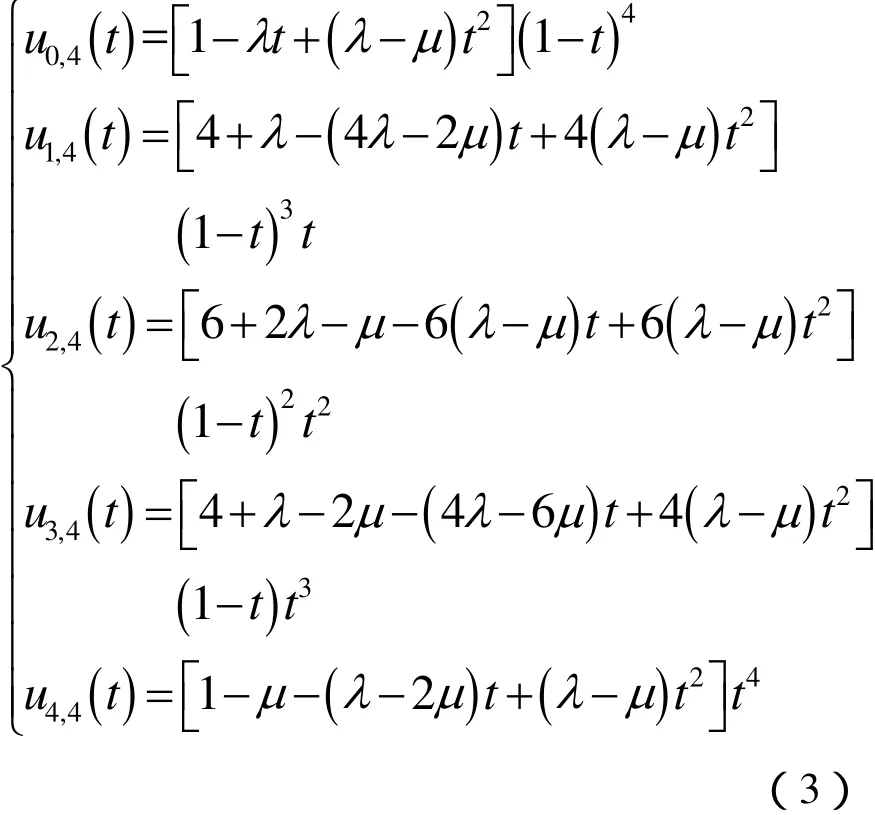
为带形状参数,λ μ的第2类基函数，简称为第2类λμ-B基。其中，当λ=μ时，-4≤λ,μ≤1；当λ≠μ时，-2≤λ≤2，-2≤μ≤1。图2给出了λ=-1，μ=0时的第2类基函数图形。

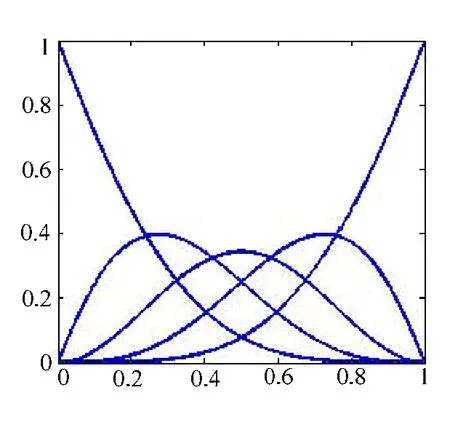
图2 λ =-1, μ =0时的基函数

性质5 退化性 当==0λ μ时，式(3)退化为四次Bernstein基，当=0λ μ≠时，式(3)退化为文献[5]中的第1类λ-B基。此性质说明，式(3)是四次Bernstein基的扩展。

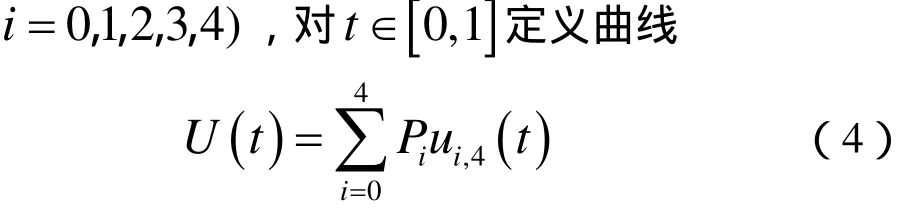
称式(4)所定义的曲线为带有形状参数,λ μ的第2类六次 Bézier曲线，简称为第 2类六次λμ-Bézier曲线。显然当==0λ μ时，第2类六次λμ-Bézier曲线退化为四次Bézier曲线。

由第 2类基函数的性质可得曲线(4)具有以下性质：

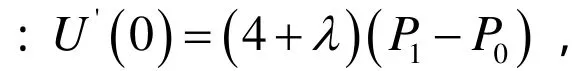
性质2 凸包性。

性质3 对称性。

性质4 几何不变性和仿射不变性。

性质5 变差减少性质(V.D.)。

3 曲线的连接

此处以第1类曲线为例加以说明，第2类曲线的连接类似。

给出2条不同的第1类六次λμ-Bézier曲线

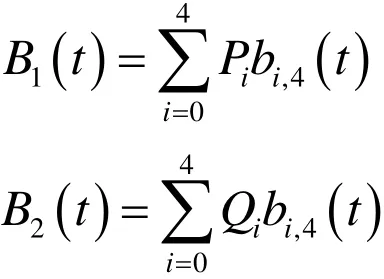
其中P4=Q0，B1（t）中的参数为λ1,μ1，B2（t）中的参数为λ2,μ2，则有：

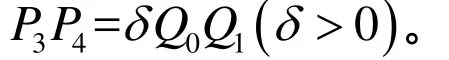
4 形状参数的几何意义

此处仍以第1类六次λμ-Bézier曲线为例加以讨论，第2类可类似讨论。

将第1类基函数改写为

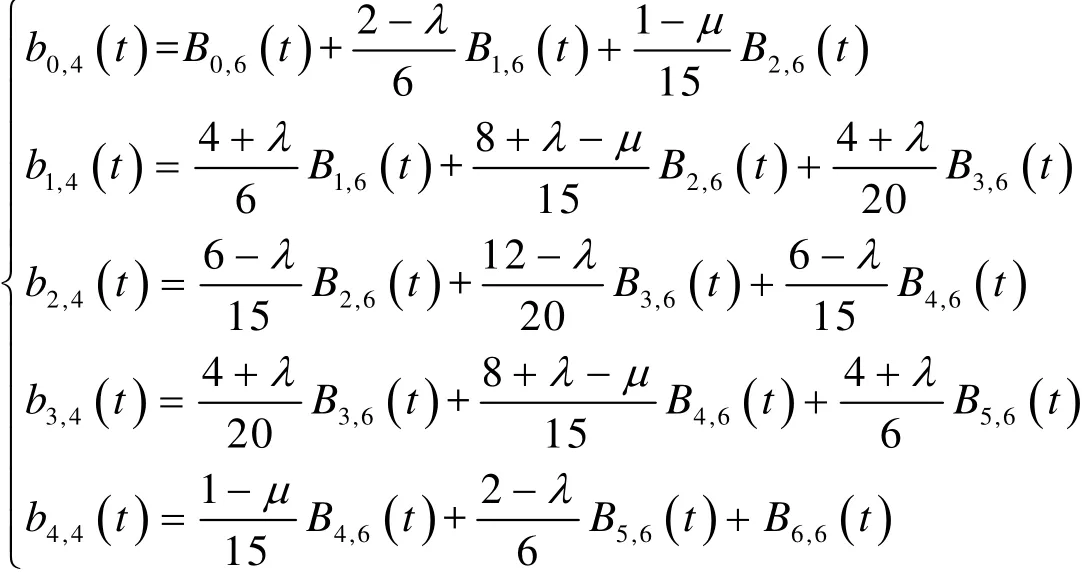
上式改写为矩阵形式为

则可用六次 Bézier曲线表示第 1类六次λμ-Bézier曲线，其中iV为此六次Bézier曲线的控制顶点。由式(5)、(6)可得此六次 Bézier曲线与第1类六次λμ-Bézier曲线的控制顶点之间的关系式为

5 曲线的应用实例

图 3是第 1类当λ=-2,-1,0,1,2时开曲线的花瓣图形；图 4是第 2类当λ=-2, -1, 0, 1, 2时开曲线的花瓣图形；图5是第1类当μ=-2, -1, 0, 1时开曲线的花瓣图形；图6是第2类当μ=-2, -1, 0, 1时开曲线的花瓣图形。从图形可知，对于相同的控制多边形，两类曲线有不同的特性。

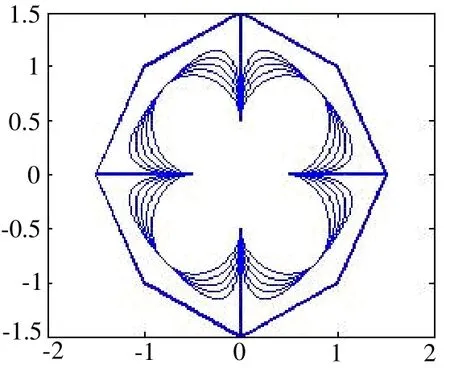
图3 第1类曲线固定μ=1的花瓣图形

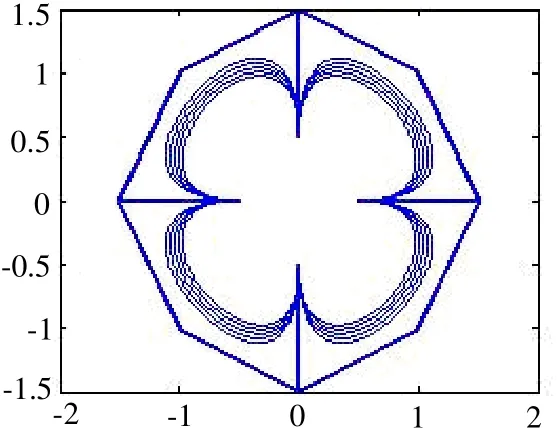
图4 第2类曲线固定μ=1的花瓣图形

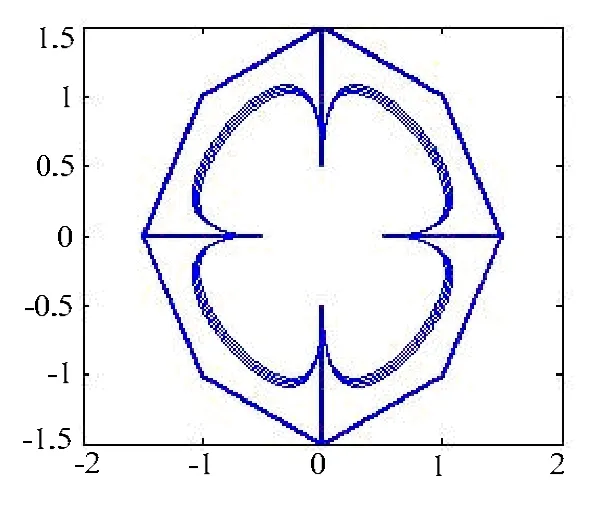
图5 第1类曲线固定λ=1的花瓣图形

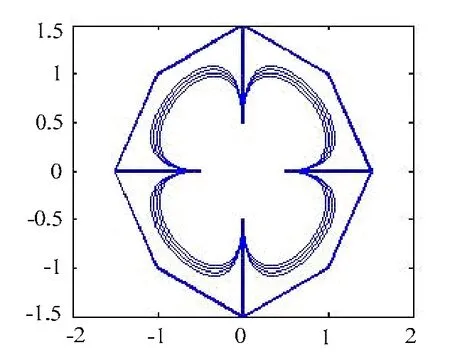
图6 第2类曲线固定λ=1的花瓣图形

6 曲面的定义

运用张量积的方法，可将两类曲线推广到曲面上。现仅以第1类曲线为例。

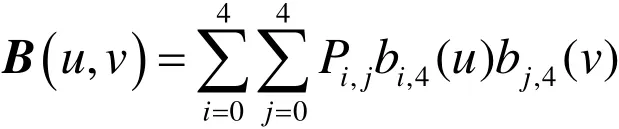
其中u,v∈[0,1]。称为[0,1]×[0,1]上的第1类双六次λμ-Bézier曲面，可证明第 1类双六次λμ-Bézier曲面具有与四次Bézier曲面类似的性质。

7 结 束 语

给出的曲线生成方法，以四次Bézier曲线为特例，保留了Bézier曲线的几何性质。在形状参数的取值范围内，选择不同的参数值，可生成逼近于同一控制多边形的不同的曲线，且超出了一般的四次 Bézier曲线和五次λ-Bézier曲线对控制多边形的逼近。而且这里形状参数具有明确的几何意义，设计者可以根据自己的需要来调整参数值以达到设计需要。运用张量积方法，将曲线推广到曲面，曲面的形状是可调的且具有和曲线类似的性质。

[1]施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京：高等教育出版社, 2001：306-454.

[2]齐从谦, 邬弘毅. 一类可调控 Bézier曲线及其逼近性[J]. 湖南大学学报, 1996, 19(1)：15-19.

[3]韩旭里, 刘圣军. 二次 Bézier曲线的扩展[J]. 中南工业大学学报(自然科学版), 2003, 34(2)：214-217.

[4]吴晓勤, 韩旭里. 三次 Bézier曲线的扩展[J]. 工程图学学报, 2005, (6)：98-102.

[5]吴晓勤, 韩旭里, 罗善明. 四次Bézier曲线的扩展[J].工程图学学报, 2006, 27(5)：98-102.

[6]吴晓勤. 带形状参数的 Bézier曲线[J]. 中国图象图形学报, 2006, 11(2)：269-274.

[7]朱秀梅, 郭清伟, 朱功勤. 含多参数的Bézier曲线的扩展[J]. 合肥工业大学学报(自然科学版), 2008,31(4)：671-674.

Extension of quartic Bézier curve with two shape parameters

Liu Xiaoqiong，Yang Guoying
( College of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo Henan 454000, China )

Two classes of six degree polynomial basis functions with two shape control parameters λ and μ are presented. They are extensions of quartic Bernstein basis functions.Properties of these two bases are analyzed and the corresponding polynomial curves with two parameters λ and μ are defined accordingly. These curves not only inherit the outstanding properties of quartic Bézier curve, but also can be adjusted in shape by changing the value of λ and μ without the changing of control points. The parameters have obvious geometric meaning.When λ=μ=0, the curve degenerates to four degree Bézier curve. Experiments show that the method given in this paper is intuitive, effective and easy to control.

curve design; quartic Bézier curve; shape parameters

TP 391.72

A

2095-302X (2013)01-0041-05

2011-07-04；定稿日期：2011-09-14

河南省教育厅自然科学基金资助项目（2009B110009）；河南理工大学青年基金资助项目（Q2012-14）

刘小琼（1980-），女，河南焦作人，讲师，主要研究方向为计算机辅助几何设计。E-mail：liuxiaoqiong@hpu.edu.cn