反应活化能的Tolman解释*

刘国杰 黑恩成

(华东理工大学化学系 上海 200237)

自从Arrhenius提出活化能概念以来，这个概念的物理意义一直引人关注。20世纪20年代，Tolman用统计力学的观点给出了明确的解释，但直至20世纪70年代才广泛被人们接受。然而，Arrhenius方程是个经验方程，由此引出的Arrhenius活化能并不严格，这就需要对化学反应活化能的解释作进一步的探讨，本文的目的就在于此。

1 Arrhenius活化能的Tolman解释[1]

Tolman解释的一个基本假设是认为，反应系统基本处于平衡状态，以致其能量服从Boltzmann分布。对于单分子基元反应:

如果反应物分子在其能级上的分布为：

能级ε0，ε1，ε2，…，εj，…

简并度g0，g1，g2，…，gj，…

浓度cA0，cA1，cA2，…,cAj，…

速率常数k0，k1，k2，…，kj，…

其中，cAj为处于j能级的反应物浓度，kj为这种反应物的反应速率常数，则由统计力学观点，处于j能级的反应物分子的反应速率当为：

(1)

反应物的总反应速率应等于各能级反应物分子的反应速率之和：

(2)

而实验测得的反应速率为:

(3)

所以，测得的反应速率常数当为:

(4)

按照Boltzmann能量分布定律:

(5)

式中Pj代表反应物分子在j能级上的分布概率，kB为Boltzmann常量。将式(5)代入式(4)，则得:

(6)

这就是说，实验测得的反应速率常数k实为相应微观量kj的统计平均值。

假定反应服从Arrhenius方程，将式(6)代入其活化能的定义式，可得:

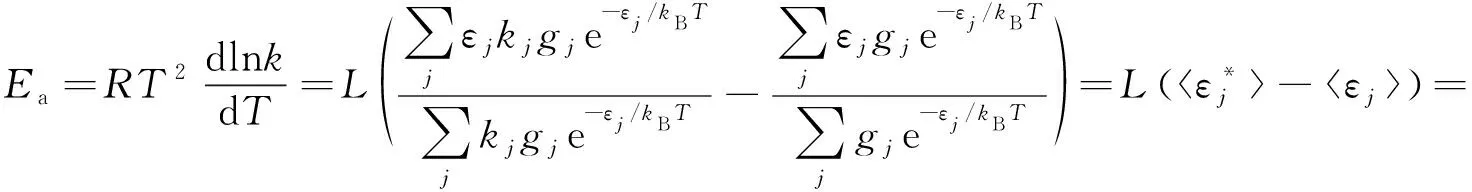
(7)

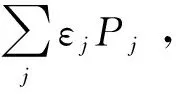
以上方法同样可应用于双分子反应:

从而得到:

(8)

式中cAi为处于i能级的反应物A的浓度，cBj为处于j能级的反应物B的浓度，kij为这两种分子间的反应速率常数。因此，实验测得的速率常数应为:

(9)

将式(9)代入Arrhenius活化能定义式，经过运算，便得:

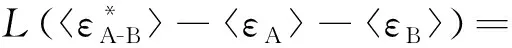
(10)

由上述推导可见，无论是单分子反应还是双分子反应，Arrhenius活化能Ea都等于活化分子或活化分子对的平均摩尔能与所有反应物分子的平均摩尔能之差。这就是Arrhenius活化能的Tolman解释。

综上所述，Tolman解释有两个前提：一是反应系统的能量必须服从Boltzmann分布，二是反应活化能必须遵守Arrhenius方程。

2 Arrhenius假设

对于反应速率常数k与温度T的指数关系，最早是由Hood[2]提出。后来，Van′t Hoff[3]从热力学考虑，得出:

(11)

假设①：并非所有分子都能反应，参与反应的只有那些能量较高的“活化分子”，一般分子必须在吸收了一定的能量后，才变成“活化分子”。这就是说，反应是按如下模式进行的：

假设②：一般分子A变成“活化分子”A*是可逆的，且“活化分子”很容易衰变为一般分子，故“活化分子”的浓度是极低的，A与A*间可视为处于平衡状态。据此，可得：

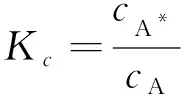
(12)

式中Kc为平衡常数，Kc=k1/k-1。

假设③：“活化分子”转变成产物P的速率很慢，这一步是反应的速控步。

(13)

故反应速率常数为:

k=k2Kc

(14)

等号两边取对数，然后对温度求导，则得:

(15)

式中代入了Van′t Hoff方程。此式即为式(11)，其中dlnk2/dT=C。所以必须补充一个假设(即假设④)。

(16)

值得关注的是，正是假设④成全了Arrhenius活化能的Tolman解释。因为据此不仅最终导得了Arrhenius方程，而且使反应系统的能量只与一般分子转变成“活化分子”的标准摩尔热力学能增量相关，而这一步是平衡过程，其能量服从Boltzmann分布。

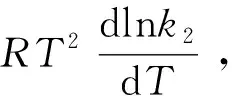
3 反应活化能及其Tolman解释

那么，k2与温度的关系如何呢？前文[6]已根据过渡状态理论导得:

k2=βTn

(17)

式中β和n是两个与温度T无关的常数。其中，β是比例系数；n是T的幂次，其值可正可负，可以是整数也可以是分数。

式(15)也可表示为：

(18)

(19)

令积分常数D=lnA，则式(19)变为:

k=k2Ae-E/RT

(20)

将式(17)代入式(20)，即得:

k=BTne-E/RT

(21)

式中B=Aβ。式(21)就是修正的Arrhenius方程，式中的E才是名副其实的反应活化能，其定义式即为式(18)。

在对实验数据的描述上，式(21)要比原始的Arrhenius方程好得多，特别是在较宽的温度范围。作为一个例子，基元反应D+H2→DH+H，Michael等[7]用闪光光解等技术测定了它在167～1980K温度范围的反应速率常数，发现它能十分满意地用下式来描述：

k=4.0×10-18T2.29exp(-21.8×103J/RT)cm3·molecule-1·s-1

NIST化学动力学数据库拟合表明，这个三参数(B、n和E)方程的拟合均方根偏差为2.24×10-14，几乎等于0，而用原始的两参数(A和Ea)Arrhenius方程拟合的均方根偏差为0.37，显然，前者要比后者好得多。拟合得到的活化能也有明显的差别：E=21.8kJ·mol-1，而Ea=29.1kJ·mol-1。文献[8]已用表列出了这两个方程拟合的结果。

那么，反应活化能E的物理意义是什么呢？这可由式(14)和式(18)看出。由式(14)可知:

这就是说，k与k2之比等同于一般分子与“活化分子”间的平衡常数，故这个比值是可用Boltzmann能量分布来描述的。再由式(18)不难看出，这个比值也遵守Arrhenius型方程，故Tolman解释同样适用于反应活化能E。

参 考 文 献

[1] Tolman R C.JAmChemSoc,1925,47:2652

[2] Hood J J.PhilMag,1878,6:371

[3] 韩德刚,印永嘉.化学教育,1981(增刊1):62

[4] Arrhenius S.ZeitPhysikChemie,1889,4:226

[5] 伊列敏 E И.化学动力学基础.陈天明译.福州:福建科学技术出版社,1985

[6] 刘国杰,黑恩成.大学化学,2013,28(2):77

[7] Michael J V,Fisher J R.JPhysChem,1990,94:3318

[8] 罗渝然,俞书勤,张祖德,等.大学化学,2010,25(3):35