基于熵权模糊物元模型的干旱区水资源承载力研究——以甘肃民勤县为例

田静宜，王新军

（复旦大学 环境科学与工程系，上海200433）

水是自然资源的重要组成部分.水资源质、量适宜，且时空分布均匀，将为区域经济发展、自然环境的良性循环做出巨大贡献；反之，水资源开发利用不当，又可制约国民经济发展，破坏生态环境.我国水资源总量虽然较多，但人均量并不丰富，且地区分布不均，这些特点决定了我国对水资源开发利用的艰巨性.水资源承载力的合理分析和评价对一个地区的综合发展和发展规模来说有着重要的影响.尤其对于干旱地区，水资源承载力已经成为区域可持续发展的重要保障.

1 水资源承载力的概念和研究方法

1.1 水资源承载力概念

1921年，人类生态学家帕克（Park）和伯吉斯（Burgess）确切提出了承载力（Carrying Capacity）这一概念[1]，并首次将其应用于研究人口问题，并指出在某一地区特定的环境条件下（主要是指生存空间、营养物质、自然资源等因子的配合），人口数量存在的最高极限.

20世纪80年代，联合国教科文组织（United Nations Educational Scientific and Cultural Organigations，UNESCO）提出了资源承载力的概念:一个国家或地区的资源承载力是指在可以预见到的期间内，利用本地能源及其自然资源和智力、技术等条件，在保证符合其社会文化准则的物质生活水平条件下，该国或地区能持续供养的人口数量[2].

水资源承载力，是继土地承载力后，在资源承载力方面开展研究最多的领域，研究成果主要集中在水资源承载力概念的定义、水资源承载力评价指标体系的选择以及水资源承载力评价模型和方法的研究等方面.但由于不同时期不同的地区，自然条件、水资源条件、社会经济系统和生态环境各不相同，使得水资源承载力具有复杂性、时效性和不确定性，其概念和内涵至今未形成统一的认知和理论体系.目前，已有众多学者对水资源承载力概念提出了各自的见解，其中惠泱河等学者[3－10]分别从水资源“最大支撑能力”、“最大支撑规模”及“最大开发量”等方面定义了水资源承载力概念，较具代表性.

通过对这些水资源承载力定义的归纳和研究，作者认为，水资源承载力应包括以下4点内涵:时空内涵、可持续发展内涵、社会经济内涵和动态性内涵[11].

因此，水资源承载力可定义为:在某一特定历史发展阶段，在一定经济社会和技术发展水平条件下，以维持生态系统和社会经济系统可持续发展为原则，经过合理配置，该区域水资源系统能够支持的合理社会经济规模.

1.2 水资源承载力的研究方法

目前，水资源承载力综合评价方法有层次分析法、模糊综合评判法、主成分分析法、多目标和多决策法、系统动力学法、基于反向传播算法（Backpropagation algorithm，BP）人工神经网络的评价等:

（1）层次分析法针对多层次结构的系统，用相对量的比较，确定判断矩阵，取特征向量作为权重，最后综合出总权重，并且排序可靠度比较高，但评价对象的因素不能太多；

（2）模糊综合评判法是在对各个因素进行单因素评价的基础上，通过综合评判矩阵对其承载能力做出多因素综合评价，克服传统数学中“惟一解”的弊端，具备可扩展性，但不能解决评价指标间的信息重复问题，隶属函数、模糊相关矩阵等的确定方法有待进一步研究；

（3）主成分分析法是对原始相关矩阵内部结构研究，找出影响某个过程的几个不相关综合指标来线性表示原来变量，通过不同承载力指标数值之间或指标与标准数值之间的对比得出水资源承载力.这种方法具有全面性、可比性，但函数意义不明确，需要大量统计数据；

（4）多属性和多目标决策方法通过化多为少、分层序列、直接求非劣解等方法来排序评价，具有描述准确，处理多决策多目标的动态对象的优点，但是无法涉及有模糊因素的评价；

（5）系统动力学方法以反馈控制理论为基础，以计算机仿真技术为手段，采用定性与定量相结合，系统分析与综合推理相集成的方法，适合于具有高阶次、非线性、多反馈、机理复杂和时空变异等特征的系统问题，但该法多用于中短期发展情况模拟；

（6）基于BP人工神经网络的评价是模拟人脑智能化处理，用BP算法，学习获取知识，并存储在神经元的权值中，能够提炼评价对象本身的客观规律并对相同属性的评价对象的进行评价.这种方法能够处理非线性、非局域性与非凸性的复杂系统，但精密度不高，需要大量的样本.

施雅风、孟凡德、张鑫等学者分别运用常规趋势法，主成分分析法，模糊综合评判法等对乌鲁木齐河流域、关中平原地区的水资源承载力进行了研究[12－19].

本文针对水资源承载力中单项指标间的不相容问题，及水资源承载力的模糊性，选择以物元分析法为基础，提出水资源承载力评价指标体系，利用熵权法确定各指标的权重，建立评价水资源承载力的熵权模糊物元模型，应用该模型对民勤地区的水资源承载力进行综合评价.

2 模糊物元模型方法原理

1983年蔡文教授提出物元分析理论[20].物元分析法是研究解决不相容问题的规律和方法的新兴理论，其主要思想是把事物用“事物、特征、量值”3个要素描述，并把这些要素组成的有序三元组的基本元称为物元，适用于多指标评价问题.

2.1 定义物元

给定事物N，其关于特征C有量值为V，以有序三元组R＝（N，C，V）作为表述事物的基本元，称为物元.如果量值V具有模糊性，则称为模糊物元，记作:

其中:R表示模糊物元；u（x）表示与特征C相应的模糊量值，也就是事物N对于其特征C相应量值x的隶属度.对于本文分析的水资源承载力来说，N就是评价样本，C为评价指标，u（x）为评价样本N对于指标C相应量值x的隶属度.

2.2 定义复合模糊物元

若水资源承载力评价样本N有n个评价指标C1，C2，…，Cn，与这些评价指标相应的模糊量值为u（x1），u（x2），…，u（xn），则称R为n维模糊物元.若以Rmn表示m个评价样本n维复合模糊物元，则u（xij）为第i个样本第j项评价指标对应的模糊量值（i＝1，2，…，m；j＝1，2，…，n），记作:

2.3 从优隶属度原则

各项评价指标Cn相应的模糊量值从属于标准方案对应评价指标相应模糊量值的隶属程度，称为从优隶属度，由此建立的原则称为从优隶属度原则.从优隶属度一般为正值，各评价指标对于方案来说，有越大越优型指标和是越小越优型指标，它们的计算公式分别由式（3），（4）表示.

越大越优型评价指标

越小越优型评价指标:

式（3），（4）中，xij表示第i个样本第j项评价指标对应的量值，maxxij和minxij为各评价指标所有量值中的最大值和最小值.

2.4 构造标准模糊物元与差平方复合模糊物元

构造样本n维标准模糊物元R0n，其中各项为复合模糊物元Rmn各项评价指标中从优隶属度的最大值或最小值，记作:

然后，以Δij（i＝1，2，…，m；j＝1，2，…，n）表示标准模糊物元R0n与复合模糊物元Rmn各项的差的平方，则得到差平方复合模糊物元RΔ，记作:

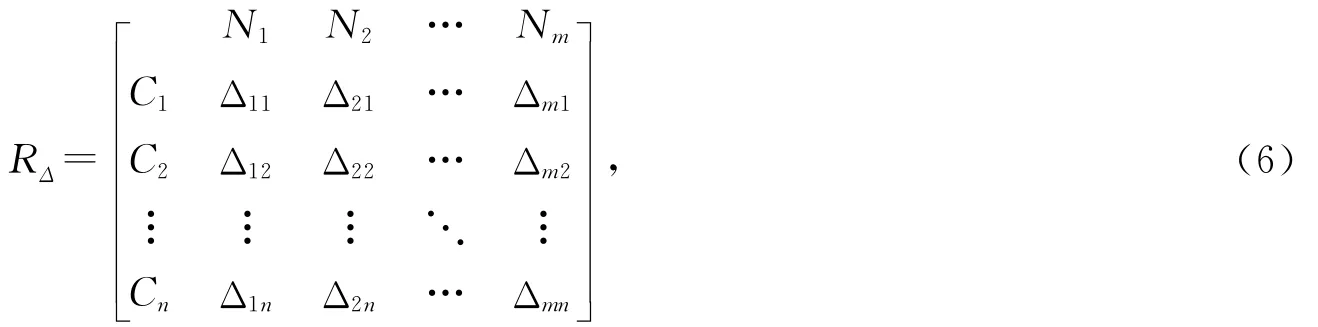
式（6）中，Δij＝[u（x0j）－u（xij）]2（i＝1，2，…，m；j＝1，2，…，n）.

2.5 熵值法确定指标权重[21，22]

在综合评价过程中，不同的评价指标对评价单元的贡献不同，需要根据其对评价单元的贡献大小确定其权重.而在确定评价指标权重时，往往多采用主观确定的方法，如层次分析法（Analytic Hierarchy Process，AHP）等方法，这样通常会导致评价结果因为人为主观因素而形成或多或少的偏差.在信息科学中，信息熵可以反映信息的无序化程度，值越小，系统越有序.在水资源承载力评价中，某项评价指标变异程度越大，说明其提供的信息量越大，其所占权重也应越大.由评价指标构成判断矩阵来确定指标权重，能在一定程度上消除权重计算的人为干扰，使评价结果更为合理.熵值法计算过程如下.

1）构建m个事物n个评价指标的判断矩阵R＝（xiij）mn（i＝1，2，…，m；j＝1，2，…，n）.

2）将判断矩阵归一化处理，得到归一化判断矩阵B，

对于越大越优型指标，有:

对于越小越优型指标，有:

式（7），（8）中，maxxij，minxij为同一评价指标下不同事物中最满意、最不满意者（越大越满意或越小越满意）.

3）定义熵:在m个评价事物n个评价指标的评价过程中，确定第j个评价指标的熵值为

4）计算熵权:

2.6 计算贴近度和综合评价

贴近度是指被评价样品与标准样品两者互相接近的程度，其值越大表示两者越接近，反之则相离较远，从而可以对样品进行优劣划分.由于水资源承载力的评价是综合评价性质，所以采用 （ · ，＋）先乘后加算法对欧式贴近度进行计算:

并构建欧式贴近度复合物元模糊矩阵RρH:

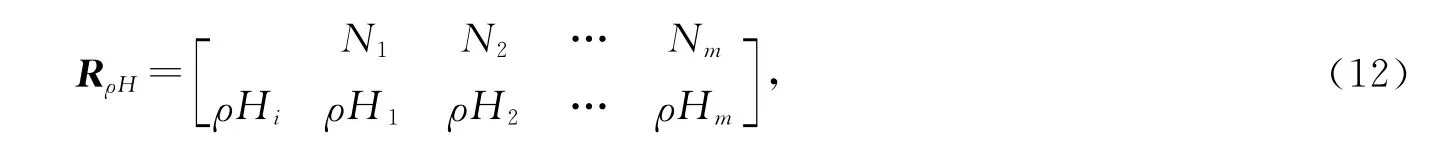
式（11），（12）中，ρHi（i＝1，2，…，m）为第i个评价样本与标准样本之间相互接近程度，以此即可对评价样本水资源承载能力大小进行评价.

3 实例研究

3.1 民勤县概况

民勤县位于河西走廊东北部，石羊河流域下游，属武威地区管辖.地理坐标在东经103°2′至104°2′，北纬38°5′至39°6′之间.境内四周高、中部低，四周被低山、沙漠环绕，地势由西南向东北倾斜，具有明显的盆地地貌特征.县域总面积为160.16×104Hm2.

民勤县东、西、北三面被腾格里沙漠和巴丹吉林沙漠包围，为典型的沙漠干旱性气候.常年干燥，降水少，蒸发大，年平均降水量115mm，蒸发量2644mm；平均相对湿度最大为53%，年平均气温7.8℃，冬冷夏热，昼夜温差悬殊，日照长，风沙多；属典型的干旱沙漠条件下的平面水文地质类型，石羊河是民勤县境内唯一的地面水资源来源，贯穿武威、民勤盆地.

从20世纪70年代开始，民勤开始大规模打井取水，1985～1995年，民勤绿洲大量开垦，破坏天然植被，使地下水急剧下降，再加之上游用水增加，导致民勤地表水量减少，草地迅速退化，绿洲面积缩小，给民勤带来了难以弥补的生态债务.

3.2 评价指标体系选取

水资源承载力评价指标体系的选取是水资源承载力综合评价中的一个关键问题.人口、社会经济发展以及资源环境是个巨大复杂的系统，如何来描述这三者发展规模、质量及相互联系对水资源承载力的影响，仍需进一步讨论研究.

在目前已有的研究成果中，傅湘、葛吉琦等学者[23，24]利用分项指标体系将评价指标分成若干单项指标，而肖满意[25]、来海亮[26]等学者则将水资源承载力评价指标分成几大类，每一类下又分成若干个子指标，然后根据具体情况再对评价指标进行精简.

根据已有研究成果[26]，本文采用驱动力－状态－响应（Driving force－state－Response，DSR）框架作为评价指标体系的逻辑框架.水资源承载力综合评价不仅是一种水资源状态评价，还要考虑影响这种状态的驱动力以及针对驱动力所做出的政策响应.三者关系如图1.

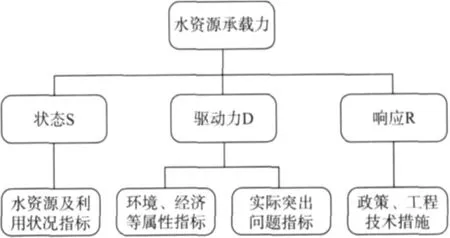
图1 水资源承载力评价指标体系逻辑框架Fig.1 Assessment index system log frame of the carrying capacity of water resources

“状态”部分构建水资源及其开发利用状态描述指标体系.“驱动力”部分包含与水资源及其开发利用相关的环境、经济属性指标体系和反映实际突出问题的指标体系，“响应”部分考虑到已有《石羊河流域重点治理规划》等相关措施，政策性较强，故不再提出具体评价指标.

由于评价区域的特异性，评价指标的选取需根据评价区域特点进行选择.水资源的开发和利用是个极其复杂的系统，涉及水资源的自然属性、水资源开发利用状况、区域环境现状、社会经济系统等众多方面，为此，对照水资源开发利用的影响因素，分别选取水资源自然属性及利用状况指标，环境、经济属性指标；进而，以民勤县的实际问题为导向，针对其水资源本身及开发利用中出现的问题，提出实际缺水问题诊断指标及标准，从而构建描述民勤水资源承载力的评价指标集.

根据民勤生态环境现状特点，选取石羊河流域重点治理规划中的现状年与规划年作为评价年份（本文中2003、2010年的数据均为实际数据，2020年为规划数据），具体指标选取如表1.

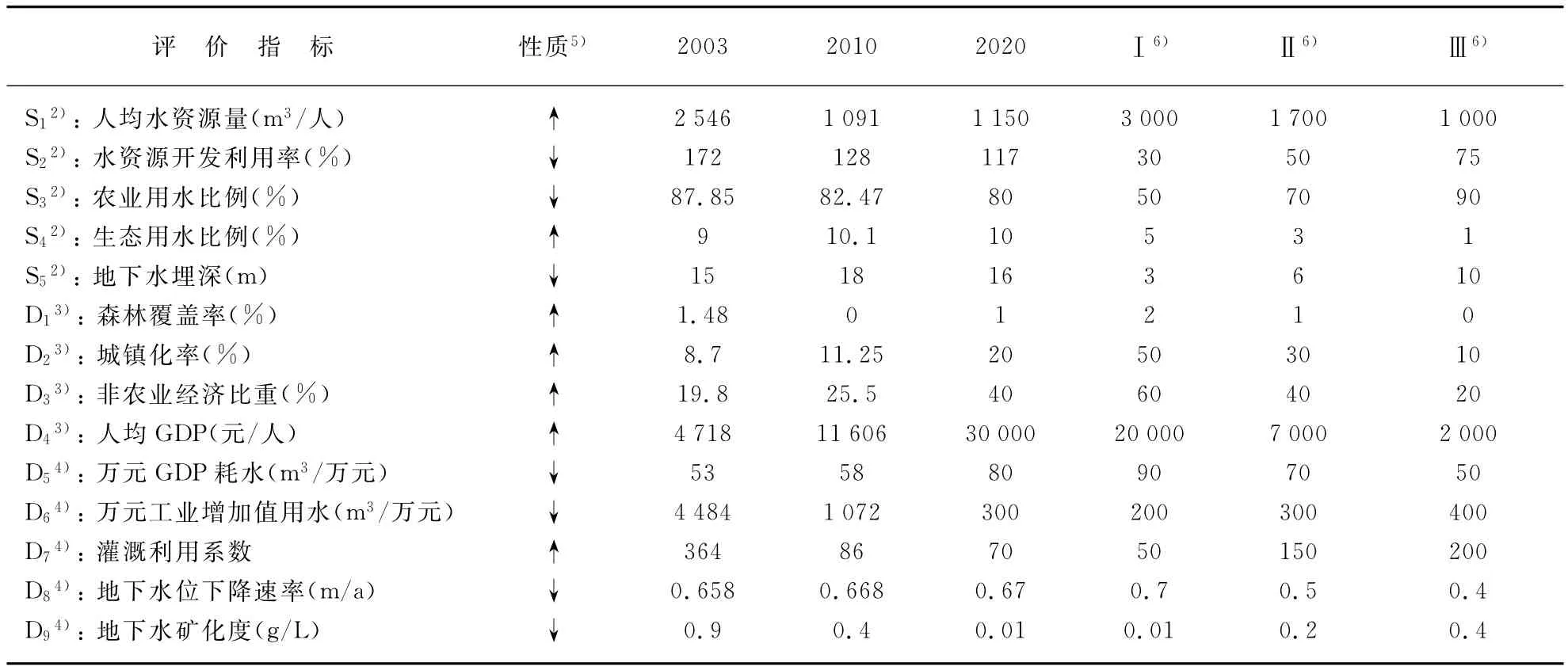
表1 民勤水资源承载力评价指标体系及评级标准值1）Tab.1 Assessment index system of the carrying capacity of water resources in Minqin and classification standard of assessment factors1）

3.3 建立评价模型

根据前文的模糊物元方法原理，建立民勤水资源承载力评价模型:

1）构建复合模糊物元，对民勤3个规划年和评级标准建立6个样本、15个指标的复合模糊物元；

2）根据式（2），（3）从优隶属度原则和指标性质，构建从优隶属度复合模糊物元（Rmn），

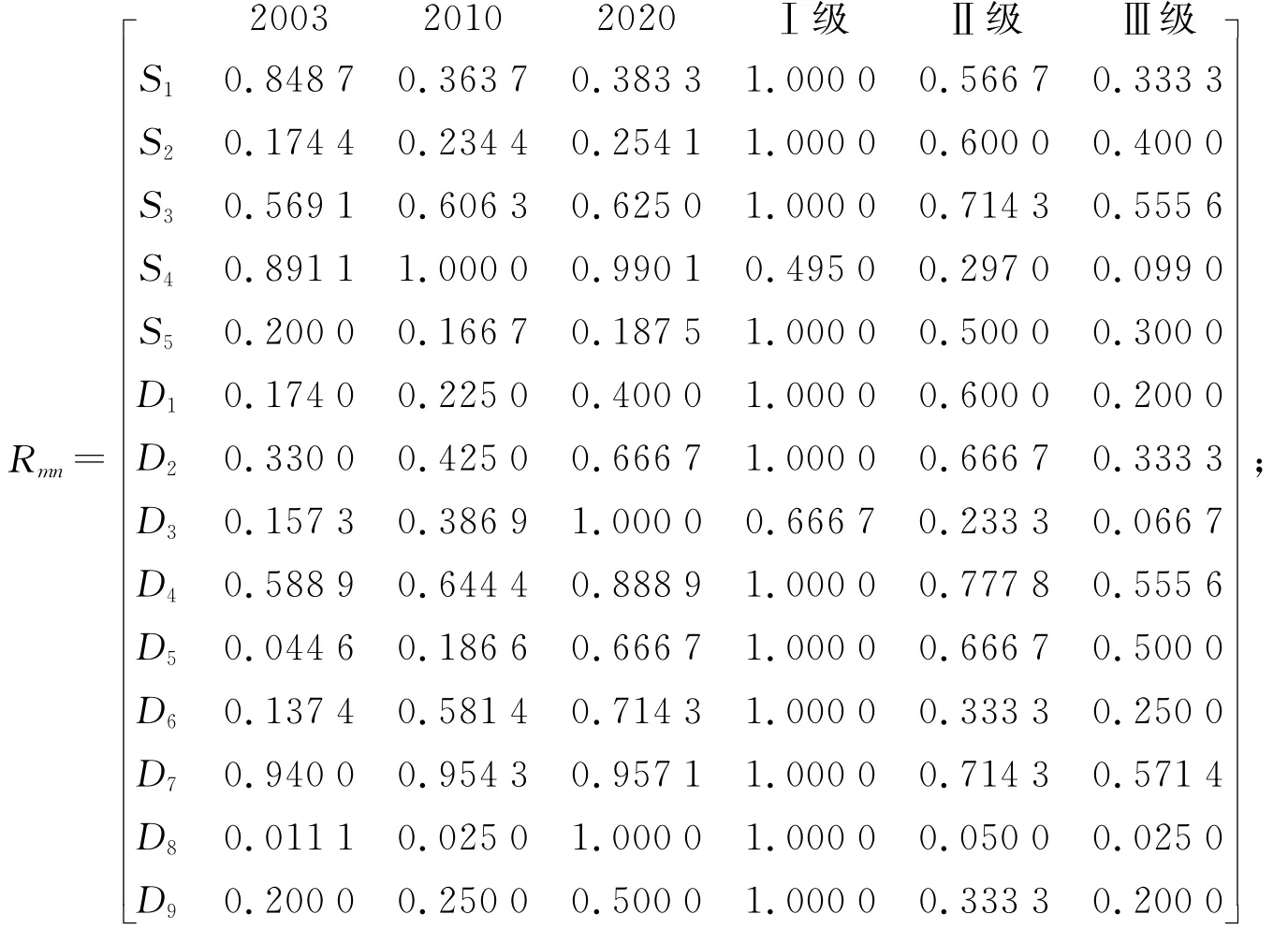
3）根据式（5），（6），构建差平方模糊复合物元（RΔ）:

4）用熵值法计算各指标权重:各指标的实际值按式（7），（8）进行归一化处理得到判断矩阵，再由式（9）计算各指标的熵（Hj）:

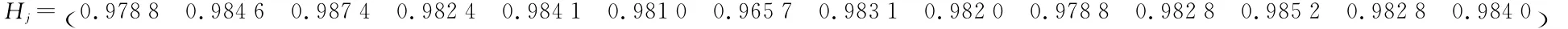
并由式（10）得到各指标权重:

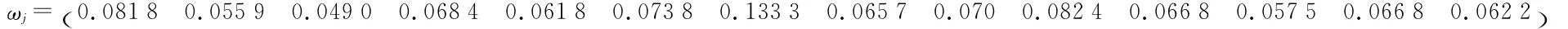
5）由式（11），（12）可得各样本的贴近度:

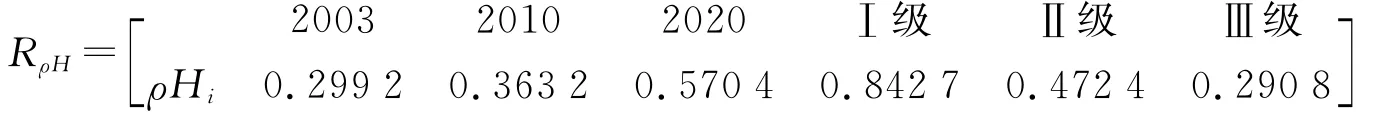
3.4 结果分析

运用本文建立的模型计算得到的民勤2003、2010和2020年的水资源承载力结果如表2.

从结果中可以看出，民勤在2003年水资源承载力达到Ⅲ级，水资源开发利用已经到了相当高的程度，基本无进一步开发的潜力，水资源的短缺已经威胁到生态环境及国民经济的发展，需要采取相应的政策和措施；2010年的民勤水资源承载力仍为Ⅲ级，但是已比2003年情况有所好转，说明石羊河流域重点治理规划对民勤水资源承载力及生态恢复是切实有效的，到2020年，民勤的水资源承载力提升为Ⅱ级，水资源的供给将在一定程度上满足民勤经济发展的需求和生态恢复的需要，绿洲生态状况进一步好转.这与马金珠等[31]利用多目标层次评价得出的“由于节水水平的提高、产业结构的调整、退耕还林还草以及污水处理等措施的实施，使民勤县的生态环境有所改善，2020年水资源状况优于2010年，2010年优于2005年”结论是相一致的.

利用模糊物元模型对水资源承载力进行评价，计算便捷；采用熵值法能够从数据本身所反映的信息无序化程度确定水资源承载力各指标的权重，有效地避免了权重分配中的主观因素，使权重计算更为客观、合理.在运用熵权物元模型过程中，指标选取尤为重要，作者在最初将当年干旱程度作为评价指标，由于2010年相比2003年降水较少，得出2010年的水资源承载力不如2003年，这与实际情况不符，对于蒸发量远远大于降雨量、依靠跨区域调水的干旱区来说，当年降水量是否大于多年平均量对民勤当年的水资源承载力并没有很大影响，所以作为评价指标并不合理.因此，适应研究区域特点的水资源承载力指标体系还值得进一步研究和完善.

表2 民勤水资源承载力评价结果Tab.2 Assessment result of the carrying capacity of water resources in Minqin

[1]Park R E，Burgess E W.An Introduction to the Science of Sociology[M].Chicago:The University of Chicago Press，1921.

[2]UNESCO，FAO.Carrying capacity assessment with a pilot study of Kenya:A resource accounting methodology for sustainable development[M].Paris and Rome:FAO，1985.

[3]惠泱河，蒋晓辉，黄 强，等.二元模式下水资源承载力系统动态仿真模型研究[J].地理研究，2001，5（2）:191－198.

[4]施雅风，曲耀光.乌鲁木齐河流域水资源承载力及其合理利用[M].北京:科学出版社，1992.

[5]王 浩，陈敏建，何希吾，等.西北地区水资源合理配置与承载能力研究[J].中国水利，2004（22）:43－45.

[6]冯尚友，刘国伞.水资源持续利用的框架[J].水科学进展，1997，8（4）:301－307.

[7]阮本青，沈 晋.区域水资源遁度承载能力计算模型研究[J].水土保持学报，1998，4（3）:57－61.

[8]孙鸿烈.中国资源科学百科全书[M].北京:中国大百科全书出版社，2000.

[9]许有鹏.干旱区水资源承载能力综合评价研究:以新疆和田河流域为例[J].自然资源学报，1993，8（3）:229－237

[10]夏 军，朱一中.水资源安全的度量:水资源承载力的研究与挑战[J].自然资源学报，2002，17（3）:262－269.

[11]李令跃，甘 泓.试论水资源合理配置和承载能力概念与可持续发展之间的关系[J].水科学进展，2000，11（3）:307－313.

[12]新疆水资源软科学课题研究组.新疆水资源及其承载力的开发战略对策[J].水利水电技术，1989（6）:2－9.

[13]徐中民.情景基础的水资源承载力多目标分析理论及应用[J].冰川冻土，1999，21（2）:99－106.

[14]郭 武.柴达木盆地水资源开发利用现状分析[J].干旱区地理，1997，20（3）:82－89.

[15]李丽娟，郭怀成，陈 冰，等.柴达木盆地水资源承载力研究[J].环境科学，2000，21（2）:20－23.

[16]陈 冰，李丽娟，郭怀成，等.柴达木盆地水资源承载方案系统分析[J].环境科学，2000，21（3）:16－21.

[17]孟凡德，刘贤赵.烟台市水资源承载变化的驱动力研究[J].烟台师范学院学报，2003，19（1）:46－50.

[18]张 鑫，王纪科，蔡焕杰.区域地下水资源承载力综合评价研究[J].水土保持通报，2001，2l（3）:24－27.

[19]陈衍泰，陈国宏，李美娟.综合评价方法分类及研究进展[J].管理科学学报，2004，7（2）:69－79.

[20]蔡 文.物元模型及应用[M].北京:科学技术文献出版社，1994.

[21]邱菀华.管理决策与应用熵学[M].北京:机械工业出版社，2001.

[22]闫文周，顾连胜.熵权决策法在工程评价中的应用[J].西安建筑科学大学学报，2004，36（1）:98－100.

[23]傅 湘，纪昌明.区域水资源承载能力综合评价——主成分分析法的应用[J].长江流域资源与环境，1999，8（2）:168－172.

[24]葛吉琦.水资源可持续利用评价[J].科技经济，1998，11（增刊）:26－29.

[25]肖满意，董翊立.山西省水资源承载能力评估[J].山西水利科技，1998（4）:5－11.

[26]来海亮，汪党献，吴涤非.水资源及其开发利用综合评价指标体系[J].水科学进展，2006，17（1）:95－101.

[27]戴晟懋，邱国玉，赵 明.甘肃民勤绿洲荒漠化防治研究[J].干旱区研究，2008，25（3）:319－324.

[28]孙 涛，王继和，刘虎俊，等.民勤绿洲生态环境现状及恢复对策[J].中国农学通报，2010，26（7）:245－251.

[29]沈天成.民勤荒漠地区水资源与水环境动态变化[J].甘肃科技，2009，25（21）:40－42，162.

[30]唐 曲，姜文来，陶 陶.民勤盆地水资源承载力指标体系及评估[J].自然资源学报，2004，19（5）:672－678.

[31]马金珠，李相虎，贾新颜.干旱区水资源承载力多目标层次评价——以民勤县为例[J].干旱区研究，2005，26（2）:11－16.