线性规划灵敏度分析的一个应用

杨大勇

（陇东学院 数学与统计学院，甘肃 庆阳 745000）

线性规划模型如下

现在对线性规划问题(LP)化成标准型(LP')可运用单纯形法得到最优表,设T(B)为对应的最终单纯形表,简记为：

对线性规划模型(LP)在增加约束条件的情况[1]中做了详细的说明.而对线性规划模型(LP)在减少约束条件时进行灵敏度分析,教材中提的较少.因为迭代过程已将要去掉的约束条件经过行初等变换作用于其它约束条件以及目标函数中,对整个迭代过程都产生了影响.

在前面的最终表T(B)中,最优基B的逆矩阵为B-1,线性规划模型(LP)的原m×n阶系数矩阵为A,在最终表T(B)中为即.要将第i个方程去掉,就须使第i个约束条件失灵.处理方法可在第i个约束条件左边添加两个非负虚拟变量的差xn+m+1-xn+m+2.[4]

因此,现将去掉第i个约束条件的灵敏度分析的基本思路及步骤归纳如下：

1）确定B-1的第i列向量B-1Pi;

2）在最优表中系数矩阵的最后添加B-1Pi和-B-1Pi;

3）计算相应的检验数-CBB-1Pi和CBB-1Pi,并添加到T(B)相应检验数行中;

4）判断最优性：若CBB-1Pi=0,删掉xn+m+1或xn+m+2对应的系数行（第i行）得到所求最优解;若CBB-1Pi≠0,则转入第5步;

5）删掉xn+m+1和xn+m+2对应的系数列,则得到新的单纯形表，采用单纯形法继续迭代.

例1 如下线性规划模型：maxz=-5x1+5x2+13x3

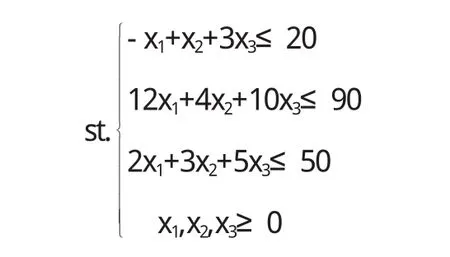
用单纯形法求解并回答：若在原问题中减少第三个约束条件,这对于最优解有何影响？

解 先将原问题化为标准型，则可列出初始单纯形表,运用单纯形法进行迭代求解,可得最终单纯形表.于是知道原问题的最优解为.现在要将第三个设备约束条件去掉,需要经过以下步骤来实现：

由于要将第三个设备约束条件去掉,从最终单纯形表中可以得出,从而有.则修改原问题的最终单纯形表,得表

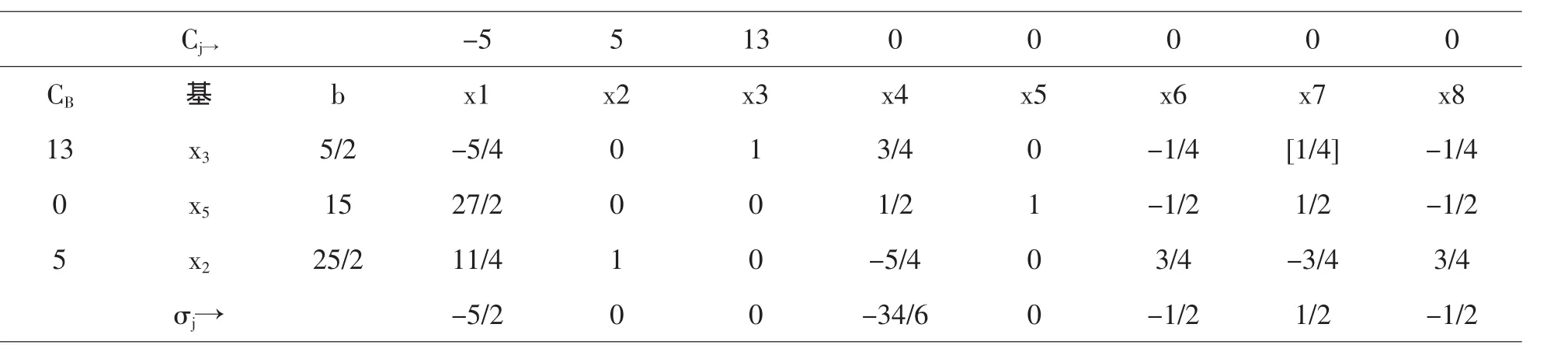
Cj→-5 5 13 0 0 0 0 0 CB基b x1 x2 x3 x4 x5 x6 x7 x813 x3 5/2-5/4 0 1 3/4 0-1/4 [1/4]-1/40 x5 15 27/2 0 0 1/2 1-1/2 1/2-1/25 x2 25/2 11/4 1 0-5/4 0 3/4-3/4 3/4 σj→-5/2 0 0-34/6 0-1/2 1/2-1/2

判别最优性,不符合条件,则x7进基,x3出基,主元素为，采用单纯形法继续迭代,得

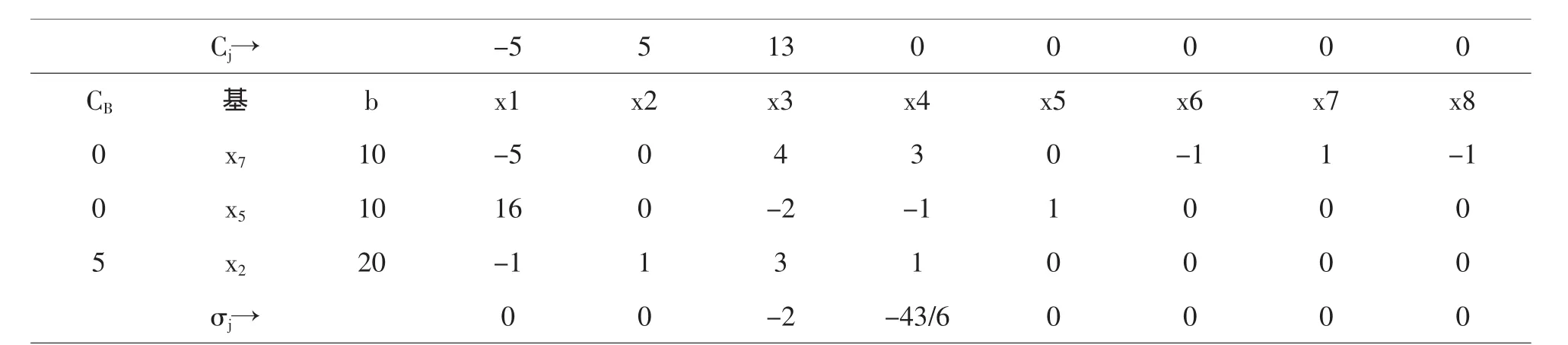
Cj→-5 5 13 0 0 0 0 0 CB基b x1 x2 x3 x4 x5 x6 x7 x80 x7 10-5 0 4 3 0-1 1-10 x5 10 16 0-2-1 1 0 0 05 x2 20-1 1 3 1 0 0 0 0 σj→ 0 0-2-43/6 0 0 0 0

删去表中基变量x7对应的系数行及x7和x8对应的系数列,显然,松弛变量x6对应的系数列也可被同时删去了,再判别最优性,已经符合条件,迭代停止.最优解为:X*=(0,20,0,0,10)T,z*=100.

本文主要针对减少约束条件的情形来对如何求最优解进行了讨论,最后给出了实例,将方法讨论中的理论付诸于实践,更有效地说明了理论的可行性和实用性.

〔1〕胡运权.运筹学[M].北京：清华大学出版社,2003.5.

〔2〕杨桂元.影子价格及其灵敏度分析[J].运筹与管理,2002,11（6）:12-13.

〔3〕李苏北.运筹学基础[M].成都：四川大学出版社,2003.1.

〔4〕解心江.线性规划模型减少约束时的灵敏度分析[J].农业系统科学与综合研究.2002,18（3）：178-179.

〔5〕徐渝,贾涛.运筹学（上册）[M].北京：清华大学出版社,2005.2.

〔6〕刘满凤,傅波,聂高辉.运筹学模型与方法教程例题分析与题解[M].北京：清华大学出版社,2001.2.

〔7〕傅家良.运筹学方法与模型[M].上海：复旦大学出版社,2006.1.