基于改进云粒子群算法的电力系统无功优化研究＊

张佩炯，苏宏升，李晓青，张吉斌

（兰州交通大学自动化与电气工程学院，甘肃兰州730070）

1 引言

无功优化是一个多约束、大规模、非线性组合优化问题。是当电力系统的结构参数以及负荷情况给定时，通过对某些控制变量的优化，来寻找在满足所有约束条件的前提下，使系统的某个或多个性能指标达到最优时的无功调节手段[1]。常用的方法主要分为经典算法和人工智能算法。

经典算法主要有线性规划法、非线性规划法、混合整数规划法等。用常规算法来求解无功优化的主要难题是离散变量的归整、多峰多极值。普遍会出现误差大、维数灾等问题，从而难以得到理想结果[2-3]。人工智能算法主要包括模拟退火算法(SA)、遗传算法(GA)、免疫算法(IA)、蚁群算法(ACA)和粒子群算法PSO)等[4-5]。这些基于群体智能的优化算法具有较强的全局搜索能力，能较好地处理离散、多目标优化问题，并在电力系统无功优化等诸多领域中得到广泛应用。但单一的算法自身不足很多，存在计算速度慢，容易陷入局部最优解等缺点。因此，采用全局搜索和局部搜索机制相结合的混合优化算法，能取长补短，提高全局搜索的能力和精度。

粒子群优化算法(PSO)是Kennedy和Eberhart于1995年提出的一种进化算法，它源于对鸟类捕食行为的模拟[6]。由于其结构简单、参数调整方便以及适合计算机编程处理等诸多优点。在连续优化问题和离散优化问题中都表现出良好的效果。但它的缺点是易陷入局部极值，搜索精度不高，进化后期收敛速度慢。

云模型是李德毅提出的一种用来定性描述和定性概念与定量数值表示之间的不确定性转换模型，已经在智能控制、模糊评测等诸多领域得到了广泛应用[7]。因此进化计算领域也开始关注云模型。传统的自适应粒子群算法通常采用惯性权重线性递减策略，而这种策略往往不能反映出实际优化搜索的过程，因此把种群分成了三个子群，分别采用不同的惯性权重生成策略，其中，普通种群的惯性权重是由云模型的X条件云发生器[7-8]来调节的。但由于基于云数字特征（期望值、熵值、超熵值）编码的云粒子群算法在配电网无功优化中易陷入局部最优，也存在早熟收敛问题，由此对该方法进行改进，改进后的方法很好地解决了云粒子群算法难于收敛的问题。在IEEE 30节点标准测试系统和电网中进行了仿真计算。

2 电力系统无功优化的数学模型

2.1 目标函数

无功优化是在保证系统无功平衡的条件下，以发电机端电压、有载调压变压器变比、补偿电容器容量等控制变量为控制手段，以降低系统网络损耗、改善电能质量为目标[9-12]。本文以从经济角度出发即有功网损最小为目标，目标函数为：

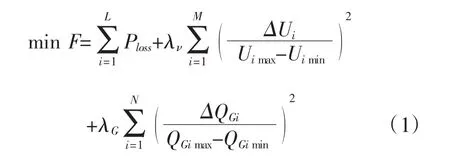
其中，N、M、L分别代表发电机的节点总数、负荷节点个数、网络所有支路数；Ploss代表系统有功损耗；Ui、Uimax、Uimin代表节点电压、电压上下限；QGi、QGimax、QGimin代表发电机节点无功出力、无功出力上限、无功出力下限；λν、λG代表越界罚系数。

ΔUi、ΔQGi的取值如式（2）所示：

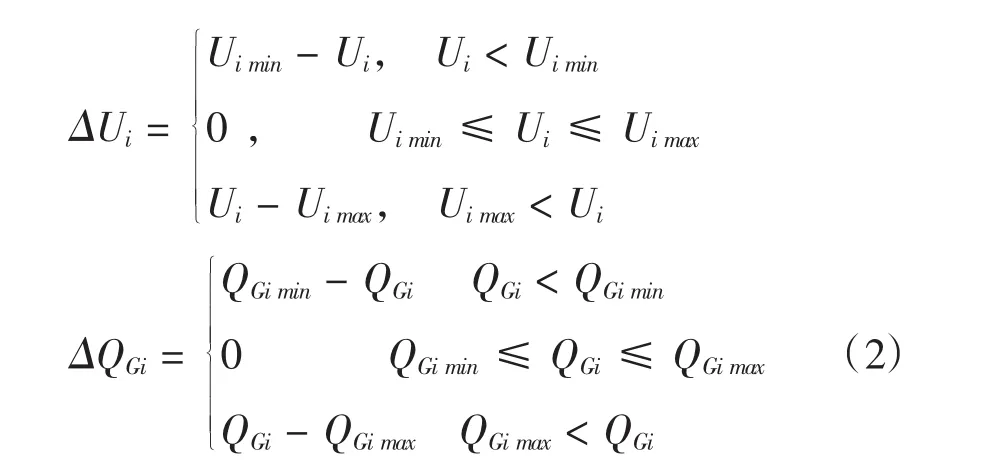
2.2 变量约束

状态变量[13-15]的约束如下：

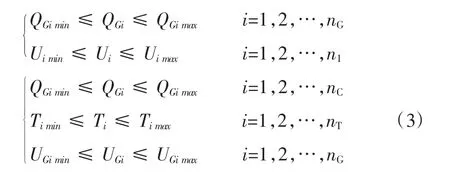
其中，QGi为发电机无功功率，Ui为负荷节点电压，QCi为电容器补偿容量、Ti为可调变压器变比，UGi为发电机端电压。

2.3 功率约束方程

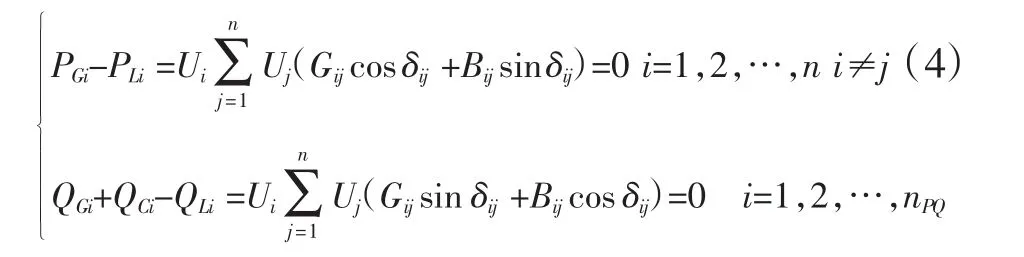
其中，PGi、QGi分别为发电机节点有功、无功出力；PLi、QLi分别为负荷节点有功、无功功率；Gij、Bij、δij分别为表节点i、j之间的电导、电纳和电压相角差；n为节点总数；nPQ为系统PQ节点个数。

3 云粒子群算法的改进

3.1 基本CPSO算法

设粒子群的大小为N，第t次迭代中，粒子Xi的适应度值为fi，粒子的平均适应度值为

将适应度值优于favg的适应度值求平均得到f'avg，适应度值次于favg的适应度值求平均得到f''avg。传统的粒子群算法，其惯性权重的计算是根据一定的迭代公式，且随着算法迭代次数的增加和适应度值的减小而线性的减小。将群体分成三个子群，ω的取法按式（8），但采用不同的进化策略。其策略为：

（1）若fi优于f'avg，则粒子的适应值较小，离最优解比较近，因此采用较小的惯性权重，进化策略采用“社会模型”，加快全局收敛的速度；

（2）若fi次于f''avg，粒子的适应值较大，离最优解比较远，采用较大的惯性权重，进化策略采用“认知模型”，使这些表现差的粒子加快收敛速度；

（3）若fi优于f''avg次于f'avg，此时粒子的适应度值适中，惯性权重采用云自适应惯性权重，进化策略采用“完全模型”[16-17]。

式（6）、（7）、（8）分别是速度更新公式、位置更新公式和惯性权重的生成规则。

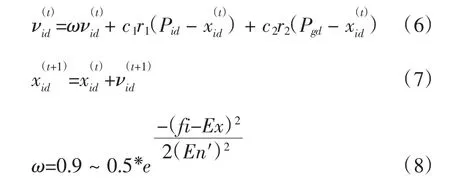
3.2 改进的云粒子群算法（ICPSO）

针对基于云数字特征（期望值Ex、熵值En、超熵值He）编码的CPSO算法存在的问题，做了如下改进：

（1）借助群体替代和解空间变换，将全局搜索与局部搜索相结合。

基本CPSO算法大部分运行时间被消耗在种群更新上，此外在进化后期，经常会出现进化较慢的局限，对此引入了群体替代和解空间变换。

群体替代的粒子群优化算法主要是通过好多个粒子群，对其解空间采用不同的搜索方式进行搜索，在这若干个粒子群中，主要搜索群体为其中一个粒子群，辅助搜索群体占多数，在搜索过程中，为了让主要搜索群粒子的多样性能得到维持，因此将一部分辅助搜索群粒子和主要搜索群粒子进行替代，从而能让主要搜索群避免因多样性的缺乏，而陷入早熟，保证主要搜索群能搜索到全局的最优点。

在CPSO中，由于粒子的遍历空间每维均是[-1,1]，为计算云粒子目前位置的优劣性，需要进行解空间的变换，将每个粒子占据的2个位置由单位空间I＝[-1,1]n映射到优化问题的解空间。记粒子Pj上第i个云算子为则相应的解空间变量为：

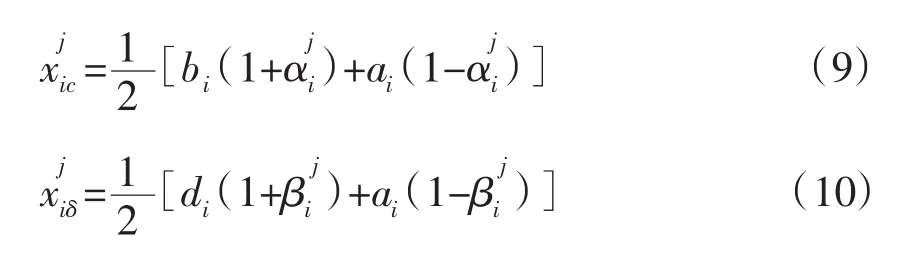
然后针对解空间变换寻优，如果所得最优值优于当代最优解，则替换当代最优解。

（2）依据正态云算子实现粒子的变异操作，来改进算法的搜索方式。

定义1变异 事先给定阈值N和K，当全局极值连续N代没有发生进化或者进化程幅度小于K时，认为粒子陷入局部极值，对全部粒子根据全局极值，通过正态云发生器进行交叉变异操作[18]。

定义2 一维正态云算子ArForwardC（Ex,En,He）是一个把定性概念的整体特征变换为定量表示的映射π:C→Π，满足以下条件[19]：

其中，Norm（μ,δ）是期望值是μ，方差值是δ的正态随机变量，N为云滴个数。利用正态云算子，把C（Ex,En,He）转换为数值表示的云滴集合，从而使概念空间与数值空间的转换得到了实现。针对基本CPSO算法进化过程中，经常出现的非当代最优解，越进化越偏离最优解的现象，改进措施如下。

种群初始化时，记录各个粒子当前的位置和速度的初始值，进而计算每个粒子的适应度，判断是否达到变异阈值N，达到则按照定义1对每个粒子进行变异操作；否则按照式（6）、（7）对粒子进行更新操作。每代结束后，将所得到的三个最优解取优，作为算法的当代全局最优解。若最优解满足适应度要求，或者迭代次数达到初设代数，则结束进化。

改进后的算法中，期望值Ex，熵值En，超熵值He，度量参数K以及变异阈值N对算法的性能有重要的影响，与此同时，惯性权重ω，加速因子C1、C2对算法的性能也有很大的影响。显然，改进措施不仅提高了种群的多样性，同时也提高了算法的搜索能力，真正体现了正态云算子对粒子进行变异操作。

4 基于改进云粒子群算法的无功优化

在CPSO算法中，由X条件云发生器产生的云滴drop(x0,μi)作为粒子，利用改进的CPSO算法进行无功优化，其中编码方式采用连续与离散变量混合实数编码，其无功优化流程图如图1所示。

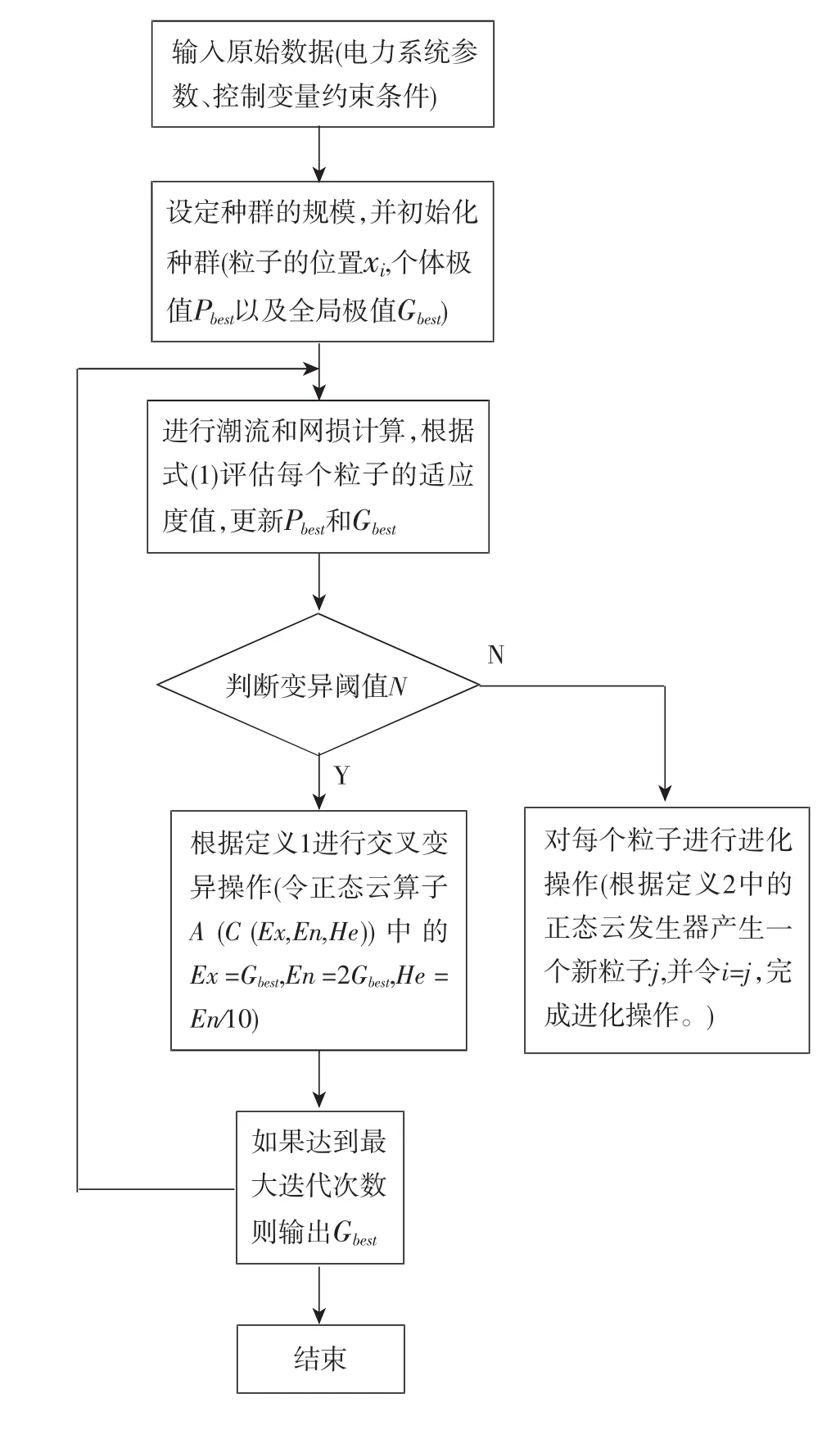
图1 ICPSO无功优化的算法流程图

在搜索空间中，粒子的位置可表示为：

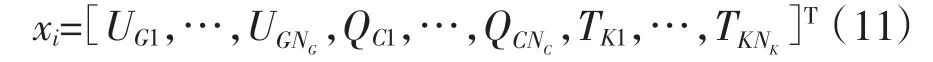
在式（11）中，位置与无功优化的控制变量相对应，UG代表发电机机端电压、QC代表可投切并联电容器补偿量、TK代表有载调压变压器变比，对于每一个粒子，维数与控制变量的个数相对应。

5 算例仿真分析

把改进后的算法在Matlab7.0上进行编程，并对IEEE30节点标准系统和电网进行了算例仿真。

IEEE30节点系统有41条支路、22个负荷节点和6个发电机节点。图2所示为IEEE 30节点标准系统。其中，节点 1、2、5、8、11、13 为发电机节点，且1为平衡节点，其余为PV节点；节点10和24为无功补偿点；电容器10的调节步长是0.1；节点24的调节步长是0.02，最大档都为5档。支路6-9，6-10，4-12，27-28为变压器支路，变压器变比范围为±8×1.25%，各发电机无功出力及电压上下限如表1所示，功率基准为SB=100MVA。

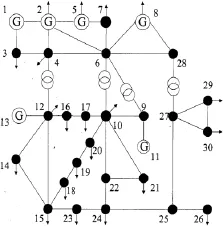
图2 IEEE30节点标准系统

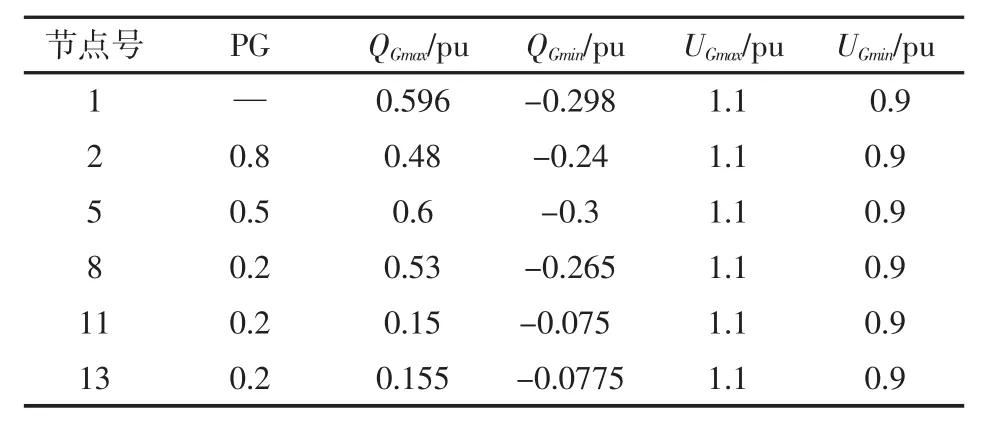
表1 PV节点的有功发电与PV节点和平衡节点的无功发电上下限值

在相同的初始条件下，分别将PSO算法、CPSO算法、ICPSO算法优化50次，种群的大小均设为100，最大迭代次数均为500，变异阈值N设为2，惯性权值ω由式(8)自行调节。取各种算法的最优平均值比较，其结果如表2所示。

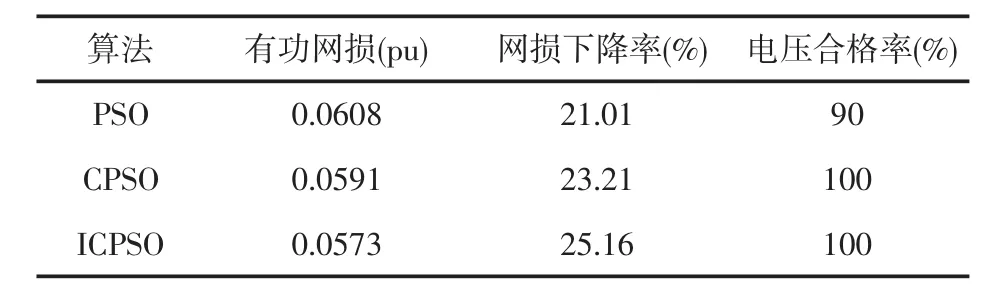
表2 IEEE 30节点标准系统不同算法优化结果比较

初始运行状态下，设置发电机的机端电压和变压器的变比均为1.0，系统总的有功网损为0.0771。本文改进的CPSO算法在无功优化后得到的系统网损为0.0573。网损下降率为25.16%。

从表2可以看出，改进后的算法所得的目标值明显优于PSO和CPSO，能够更好地获得全局最优解，且各节点电压幅值都在合格范围内，发电机的无功出力均无越限。优化后的控制变量如表3所示。

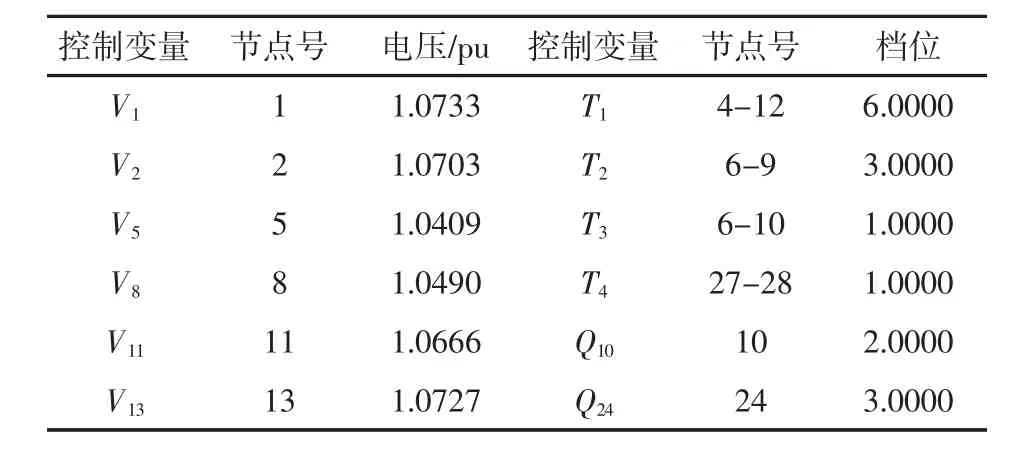
表3 优化后的控制变量

图3所示为PSO、CPSO和ICPSO三种算法的收敛特性曲线。由图2可以看出，CPSO算法的优化曲线在12次以前下降的很快，12次以后下降的很缓慢，但最终的收敛效果不理想。而ICPSO算法在3次以前下降得很快，显示了该改进算法寻优机制的有效性和优越性，3次到12次之间有一个缓冲期，在13次以后缓慢下降，在迭代23次时已经接近最优值。

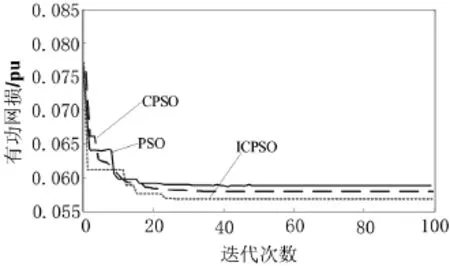
图3 PSO、CPSO和ICPSO算法的收敛特性曲线

玉门电网有12个发电机节点，54个负荷节点，71条支路，14个无功补偿点，19条可调变压器支路。将种群规模设为50，最大迭代次数设为100，对PSO算法和本文提出的改进CPSO算法各运行50次，平均优化结果如表4所示。

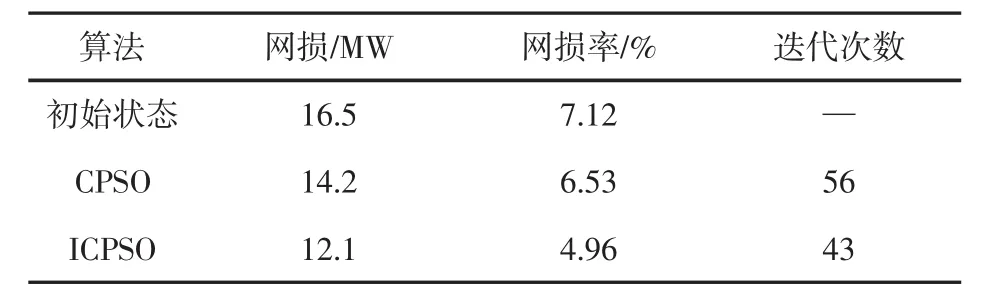
表4 玉门电网不同算法优化结果比较

从表4可以看出，本文改进后的CPSO算法网损要比基本的CPSO算法网损要降低近一个百分点，降低初始状态网损为4.4MW，找到最优解的迭代次数要比基本CPSO算法的次数要少，可见改进后的算法具有较好的收敛性和精确性。

6 结论

本文将改进的CPSO算法分别运用到IEEE30节点测试系统和玉门电网中进行无功优化。充分利用了云滴的随机性和稳定挺向性的特点，通过解空间的变换实现了全局与局部搜索方式的有机结合，并用正态云算子实现了粒子的交叉变异操作。仿真结果表明，改进后的算法在寻优速度和精度上都有了提高，并且有很好的计算效率和收敛稳定性。

［1] 张文，刘玉田.自适应粒子群算法及其在电力系统无功优化中的应用［J] .电网技术，2006，30（8）：19－23.

［2] 刘佳，李丹，高立群，等.多目标无功优化的向量评价自适应粒子群算法［J] .中国电机工程学报，2008，28（31）：22－28.

［3] 鲁忠燕，邓集祥，汪永红.基于免疫粒子群算法的电力系统无功优化［J] .电网技术，2008，32（24）：55－59.

［4] 杨晓萍，张强，薛斌，等.考虑静态电压稳定性的多目标无功优化［J] .电力系统及其自动化学报，2011，23（1）：138－144.

［5] 李惠玲，盛万兴，张学仁，等.改进小生境遗传算法在电力系统无功优化中的应用［J] .电网技术，2008，32（9）：29－34.

［6] Shi Y ，Eberhart R.A Modified Particle Swarm Optimizer［A] .in：Proceedings of 1998 IEEE International Conference on Evolutionary Computation，IEEE World Congress on Computational Intelligence［C] .Anchorage（USA）：1998.69－73.

［7] 李德毅，杜鹢.不确定性人工智能［M] .北京：国防工业出版社，2005

［8] 刘常昱，李德毅，杜鹢，等.正态云模型的统计分析［J] .信息与控制，2005，34（2），236－248.

［9] 邱威，张建华，刘念.自适应多目标差分进化算法在计及电压稳定性的无功优化中的应用［J] .电网技术，2011，35（8），81－87.

［10] 赵树本，张伏生，钟继友，等.自适应差分进化算法在电力系统无功优化中的应用［J] .电网技术，2010，34（6），169－174.

［11] 王韶，周鑫.应用层次聚类法和蚁群算法的配电网无功优化［J] .电网技术，2011，35（8），161－167.

［12] 刘述奎，陈维荣，李奇，等.基于随机聚焦粒子群算法的电力系统无功优化［J] .电网技术，2008，32（S2）：8－11.

［13] 邱晓燕，张子健，李兴源.基于改进遗传内点算法的电网多目标无功优化［J] .电网技术，2009，33（13）：27－31.

［14] 刘世成，张建华，刘宗岐.并行自适应粒子群算法在电力系统无功优化中的应用［J] .电网技术，2012，36（1），108－112.

［15] 刘红文，张葛祥.局部搜索量子遗传算法及其无功优化应用［J] .电力系统及其自动化学报，2009，21（2）：6－10.

［16] Dai C H，Chen W R，Zhu Y F，et al.Reactive power dispatch considering voltage stability with seeker optimization algorithm ［J] .Electric Power Systems Research，2009，79（10）：1462－1471.

［17] Liang J J，Qin A K，Suganthan P N，et al.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions［J] .IEEE Transaction on Evolutionary Computation，2006，10（3）：67－82.

［18] 张光卫，何锐，刘禹，等.基于云模型的进化算法［J] .计算机学报，2008，31（7）：1082－1091.

［19] 李德毅，孟海军，史雪梅.隶属云和隶属云发生器［J] .计算机研究与发展，1995，32（6）：15－20.