双转子永磁同步电机的磁路建模和磁场分析

赵锋辉

（中国重型机械研究院有限公司，陕西西安710032）

1 引言

水下航行器航行过程中需要稳定姿态，大多采用对转螺旋桨推进系统以克服陀螺效应［1]。双转子永磁同步电机［2]（双转子PMSM）有两个机械输出端口［3]，可直接驱动对转螺旋桨推进系统，比功率大、可靠性高；转矩脉动小、散热效果好、无陀螺效应，在水面舰船和水下自主航行器（UUV）等电力推进领域具有广阔的应用前景[4,5]。

文献［2]将双转子PMSM分解为内电机和外电机（定子内侧绕组和内转子构成内电机，定子外侧绕组和外转子构成外电机），讨论了其工作原理和电磁模型；文献［6]研究了双转子电机的电感参数、永磁电势及齿槽转矩；文献［7]对双转子永磁发电机进行了仿真和控制策略研究。但双转子PMSM的内外电机串联磁路和并联磁路交替出现，用传统永磁电机设计方法很难兼顾。已经研制出的样机中内外电机的转矩和转速相差较大，必须通过行星齿轮加以同步，而且须重新设计与内外转子功率匹配对转螺旋桨推进器。

本文采用特殊的永磁体结构和双转子尺寸配合方法，使双转子输出相同的转速和转矩，可直接驱动普通对转螺旋桨；采用等效磁网络模型回避了串联磁路和并联磁路问题，探讨了具有普遍意义的双转子PMSM分析方法。

2 结构和工作原理

2.1 结构

双转子PMSM由一个定子和内外两个永磁转子组成，通过单端同心双轴输出机械功率。外转子的内表面和内转子的外表面都安装永磁体［8]，如图1所示。定子内外两侧统一开槽，电枢由一套绕组按照螺线管方式绕制而成，电枢内外两层绕组的相序相反［6]，如图2所示，通入一组对称三相交流电，即可在两层气隙中分别产生等速而异向旋转的磁场。绕组端部大大缩短，效率可大幅提高。定子内外气隙都得到利用，功率密度可大幅提升。

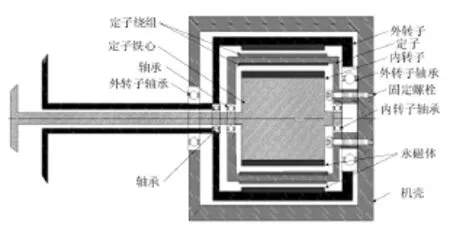
图1 双转子PMSM的结构

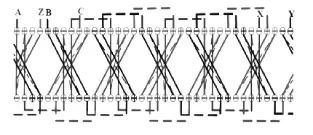
图2 双转子PMSM的绕组端部

2.2 转矩设计

内外电机的电枢串联，电流相等。根据电机工作原理，可得内电机和外电机的电磁关系：

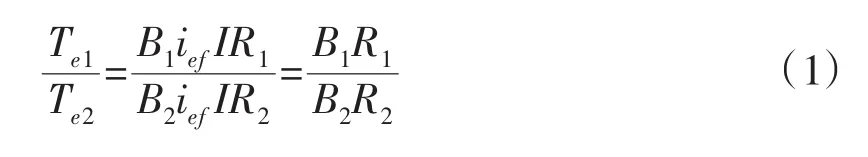
式中：R1,R2;B1,B2;Te1,Te2分别为内外转子的半径、气隙磁密和电磁转矩，lef为电枢有效长度，I为电枢电流。由式（1）可知，设计两转子的转动惯量与阻尼系数相等，内转子采用钕铁硼永磁体增大气隙磁密，外电机采用铁氧体永磁体节省成本，当内外气隙磁密和转子半径成反比时，两转子产生等大而反向的电磁转矩，驱动两个转子等速异向旋转。

3 等效磁网络模型

3.1 磁路变化特点

根据电机双气隙的结构特点，以定子内外气隙为界，将其磁场由内而外划分为内转子磁场、定子耦合磁场和外转子磁场［9]3个部分。内外转子等速异向旋转，其永磁体的相对位置周期变化，内转子磁场和外转子磁场不因两转子异向旋转而改变，但定子铁心磁路随转子相对转动而周期变化，每个周期内3种磁路（串联磁路、并联磁路和常规磁路）交替出现。

当内外转子永磁体同向对齐时，二者产生的径向磁通在定子铁心中接续，全部径向穿过定子轭部，内外磁通在定子铁心中形成串联磁路，如图3（a）所示；当内外转子永磁体反向对齐时，二者产生的径向磁通在定子铁心处转弯，全部切向流经定子轭部，内外磁通在定子铁心中形成如图3（b）所示的并联磁路；除了以上两种特殊情况，其它时刻两转子永磁体只有部分重合，二者产生的径向磁通流经定子铁心时，路径发生曲折，斜向穿过定子轭部，如图3（c）所示。

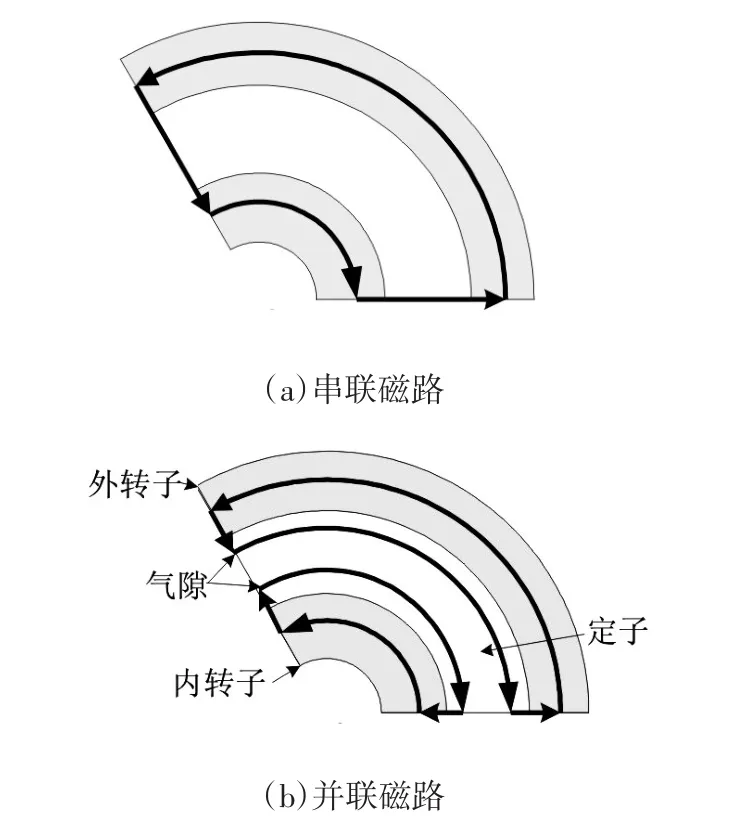
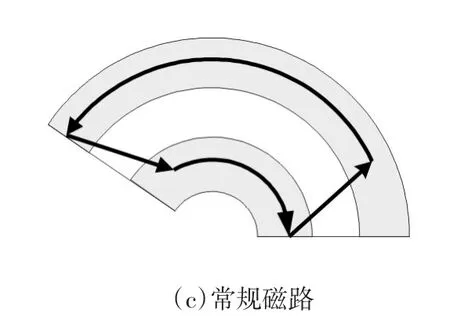
图3 双转子电机磁路图

3.2 等效磁网络模型

根据上述得到的三种磁路，省略漏磁路后，分别建立对应电机磁网络模型如图4所示。

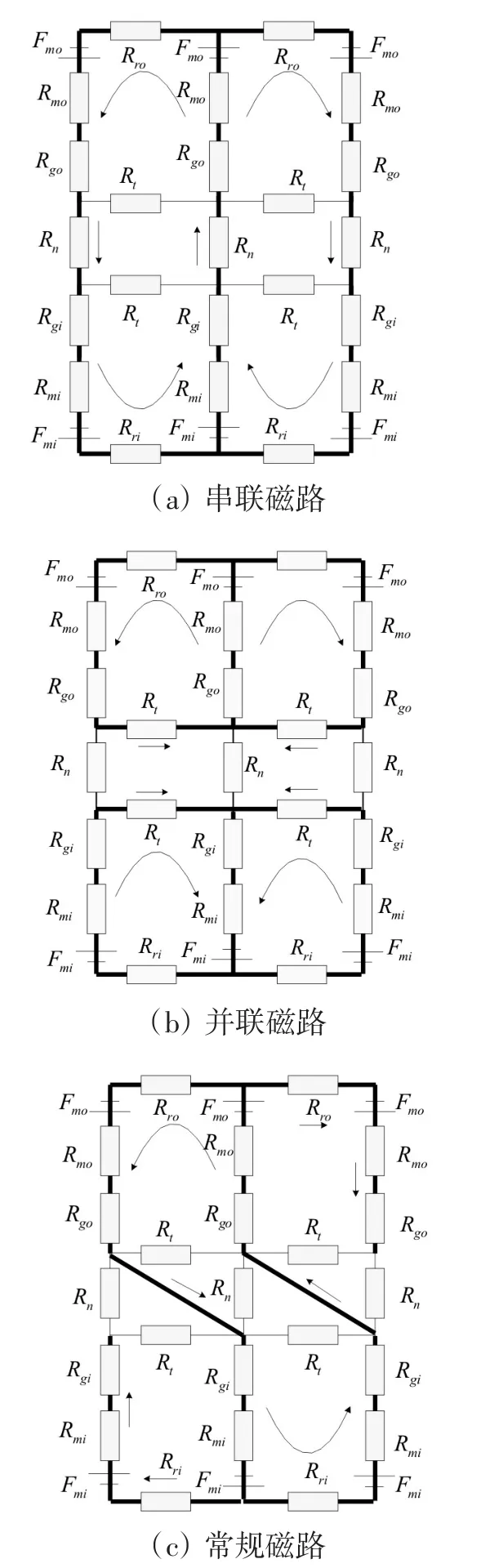
图4 电机磁网络模型

图（4）中，下标i和o分别代表内转子和外转子磁路，Rgi和Rgo分别为内外气隙磁阻，Fmi和Fmo，Rmi和Rmo分别为内外转子永磁体的磁势和内磁阻，Rri和Rro分别为内外转子的轭部磁阻。根据上述分析，将定子铁心磁阻分为切向磁阻Rt和径向磁阻Rn。Rt表征定子同侧相邻磁极在铁心中形成切向磁路的磁阻。Rn表征定子两侧相邻磁极在铁心中形成径向磁路的磁阻。

显然，磁路串联时，内外转子磁通全部径向通过定子轭部，径向磁通最大，切向磁通为零；随着两转子异向旋转，同向永磁体重合部分减小，径向磁通减小，切向磁通增大，形成常规磁路；当异向永磁体重合时，两转子形成并联磁路，内外磁通全部切向通过定子轭部，切向磁通最大，径向磁通为零。图4中加粗的磁路，分别为内外转子磁场产生的3种磁路。显然，常规磁路是径向磁路和切向磁路的过渡形式，因而定子铁心常规磁阻可看做径向磁阻和切向磁阻的合成磁阻。

3.3 磁网络模型的处理

电机的两个转子异向旋转，在定子轭部，内外电机的并联磁路和串联磁路周期更替，定子铁心磁场变化频繁，但由于铁心磁导率较高，其磁阻相对于气隙磁阻较小，故其磁路变化对整个电机磁路和气隙磁场影响较小。

由上述可知，串联磁路不需定子铁心，常规磁路只需较少的定子铁心，而并联磁路时内外电机磁通全部切向通过定子铁心。因定子轭部磁路变化对整个电机磁路影响较小，所以在电机设计时应以并联磁路为依据。图5所示为并联磁路时内电机的线性展开结构，显然，这种方法对外电机同样适合。

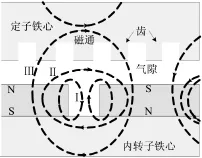
图5 内电机的线性拓扑

假设磁场未饱和，忽略电枢反应，建立包含漏磁阻的内电机等效磁路模型，如图6所示。每极永磁体的内秉磁通为φr，对外提供的磁通为φm，内磁阻为Rmi；每极永磁体与转子铁心之间的漏磁阻为Rmr；每极气隙磁通为φg，磁阻为Rgi；定子铁心切向磁阻为Rt，则图5的回路Ⅲ中，半块永磁体的内秉磁通为φr/2，对外提供的磁通为φm/2，内磁阻为2Rmi，气隙磁通为φg/2，磁阻为2Rgi，内气隙一侧定子铁心切向磁阻为2Rt，内转子铁心磁阻为Rri；回路Ⅰ中，半块永磁体和转子铁心之间的漏磁阻为2Rmr，回路Ⅱ中，两相邻永磁体之间的漏磁阻为Rmm。

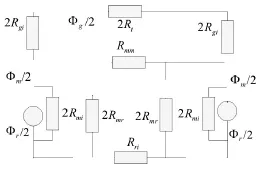
图6 内电机等效磁路模型

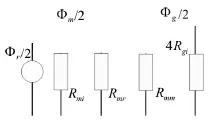
图7 内电机的简化等效磁路模型

相比气隙磁阻Rgi，定子铁心切向磁阻Rt和内转子铁心磁阻Rri可忽略。显然，两个磁通源串联，Rmi,Rmr,Rmm均并联在磁通源的两端，Rmi,Rmr,Rmm的并联磁阻Rm为：

4 电磁场计算

4.1 气隙磁密的计算

将图7通过磁通分解，可得每极永磁体向外磁路提供的磁通和气隙磁通分别为：

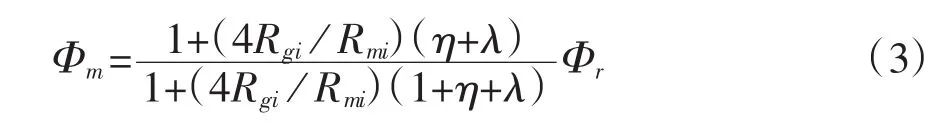
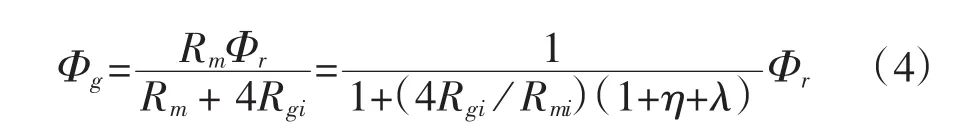
每极永磁体向外磁路提供的磁密和气隙磁密分别为：

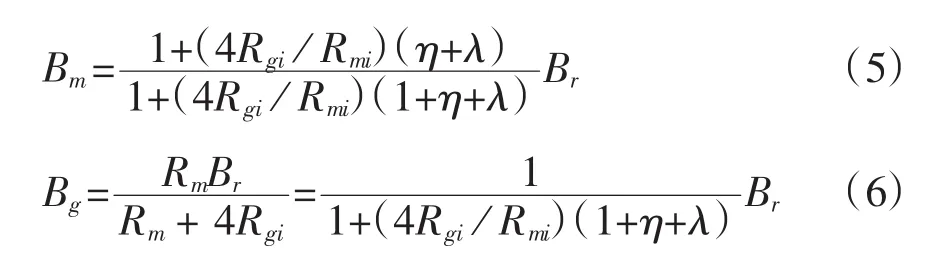
4.2 铁心磁阻的计算

定子铁心径向磁阻和切向磁阻都与转子相对位置有关，以内外电机永磁体同向（内外电机磁路串联）时为初始位置，两转子相对旋转θ角时，定子铁心磁通如图8所示。

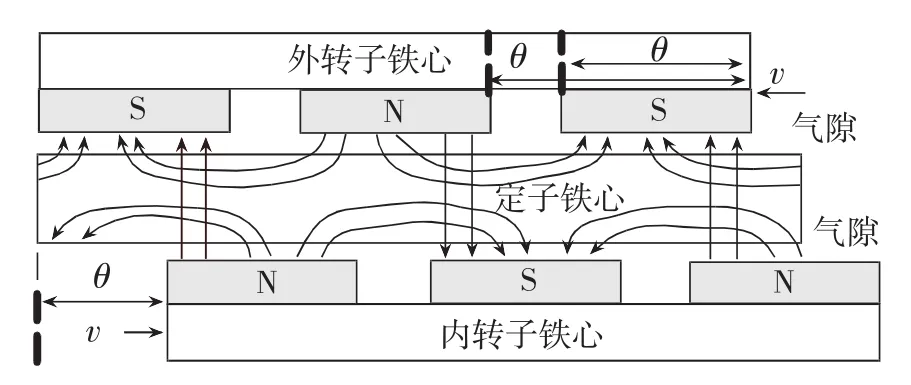
图8 内外转子相对旋转θ角时铁心磁路

根据磁路欧姆定律可得，定子铁心径向磁阻和切向磁阻的最值为：

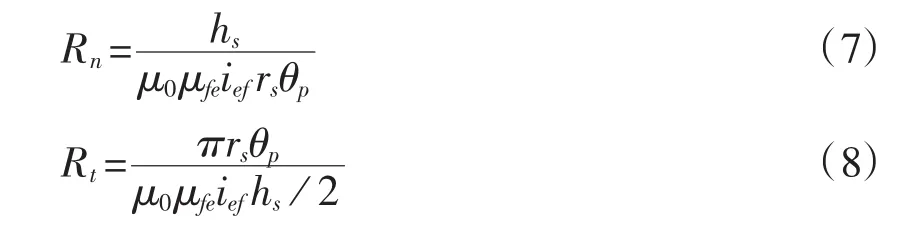
式中：θτ为极距，θp为永磁体宽度，均以弧度表示，hs为定子铁心厚度，rs为定子轭部的平均半径。

铁心磁路的变化周期为每个转子旋转两个极距所需的时间，对于一台6极电机，该周期为转子相对旋转机械角4π/3。铁心磁通为正弦变化，故定子铁心的常规磁阻（总磁阻）可由径向磁阻和切向磁阻合成：

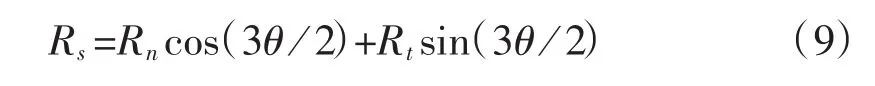
5 有限元分析

等效磁路模型能反映双转子PMSM的内部磁路特点，为了验证其正确性，对该电机进行磁场分析。两个转子的异向旋转使电机定子铁心内部磁场时空变化极其复杂，采用场路结合时步有限元方法能够较准确地考虑各种影响因素［10]，找出铁心磁通随转子位置变化的规律，与磁路计算模型分析结果进行对比，检验该计算模型的合理性。

由于该电机为对称结构，为提高计算速度，采用二维有限元磁场分析。由于该电机径向长度远比气隙大、铁心均为叠片结构的特点，假设定子表面为零矢量等磁位面，忽略集肤效应、齿槽转矩、磁滞效应和涡流效应［11]。

以一台6极双转子PMSM为例，建立磁场计算模型，该电机主要数据为：内转子内径为75mm，内转子外径为121mm；定子内径为125mm，定子外径为236mm；外转子内径为240mm，外转子外径为280mm；定子内外圆壁分别均匀开有36个槽，嵌放螺线管绕组；内外永磁体极弧系数均为0.75，内转子采用钕铁硼永磁体（Br＝1.33T，μr＝1.04342）；外转子采用铁氧体永磁体（Br＝0.42T，μr＝1.07022）。定子和转子铁心均采用DW310-35。

5.1 铁心轭部磁密分布

模型初始位置仍然是内外电机永磁体同向，通过磁场有限元计算，求取转子在不同相对位置时径向磁密和切向磁密分布，如图9所示。

初始状态为内外永磁体同向对齐，内外磁路串联，故径向磁密最大，切向磁密为0；由于内转子的相邻永磁体空隙为15°且和外转子处也对齐，双转子异向旋转0～7.5°内，只有很少的磁通形成切向磁路，故切向磁密增加很少，径向磁密减小得很慢。

从图9中还可以看出，铁心切向磁密最大值为径向磁密的2倍左右。因为电机齿槽宽度基本相等，铁心径向磁路的宽度为齿部磁路宽度的2倍，磁密最大值只有齿部的一半，故铁心径向磁路一般不饱和。铁心切向磁密和齿部最大值都设计为接近饱和值，定子和转子铁心采用同一种材料，即铁心径向磁密最大值和齿中相等，因而铁心切向磁密的最大值为径向磁密2倍左右。这样可以保证磁路并联时铁心切向磁路不饱和，同时减小铁耗和增大功率密度。

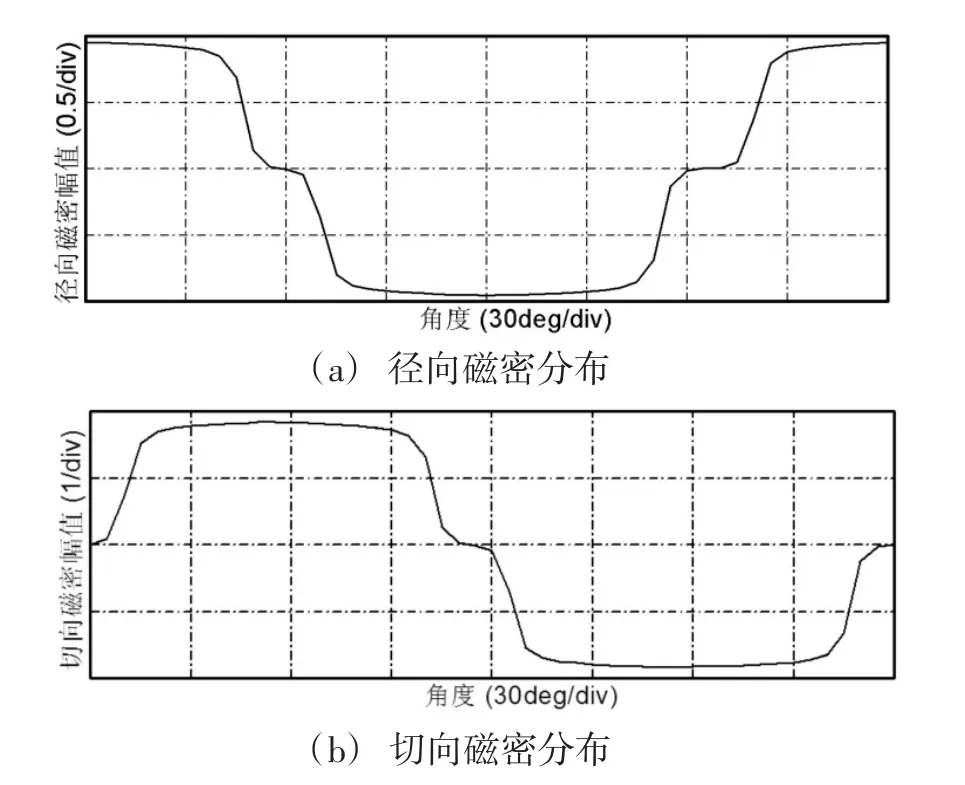
图9 磁密分布

5.2 气隙磁密分布

在空载状态下，以电机串联磁路为初始位置，双转子异向旋转240°范围内，对气隙中心处进行磁场分析，得到内外气隙磁密波形，如图10所示。在电机双转子相对位置角为0°和120°附近，内转子的相邻永磁体空隙和外转子处对齐，故气隙磁密接近0，经过异向旋转7.5°，内外电机永磁体空隙错开，气隙磁密迅速增大。内转子采用高牌号稀土永磁体，气隙磁密较高，外转子采用铁氧体永磁体，气隙磁密较低，在内外转子上采用不同材料的永磁体，通过优化内外转子半径比，使两个转子产生等大反向的转速和电磁转矩。

由图10可知，电机的齿槽效应很明显，因为电机“外转子－定子－内转子”的双气隙结构，改变定子内外槽口相对位置、改变定子内外槽口宽度、改变内外永磁体宽度、内外转子不等极等方法，使内外电机部分齿槽转矩相互抵消，再结合传统方法，减小总的齿槽转矩。

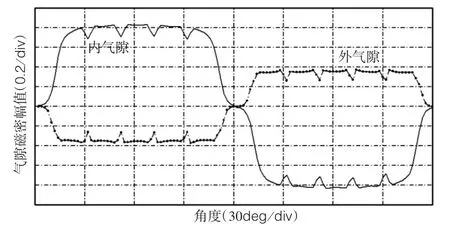
图10 双转子PMSM的气隙磁密分布

6 结束语

针对双转子PMSM双场耦合的特点，引入定子铁心径向磁阻和切向磁阻，推导出了磁阻计算方法。建立了电机的等效磁网络模型，将双耦合磁场引起的并联磁路和串联磁路交替问题简化为单一的并联磁路问题，探讨了双转子PMSM的设计方法；在内外转子上采用不同永磁体，通过设置内外转子半径比，使二者产生等大反向的电磁转矩，驱动双转子等速异向旋转。最后采用有限元方法对该电机的异向旋转磁场进行了论述，为深入分析和设计该类电机提供了依据。

［1] Pavani Gottipati.Comparitive Study of Double Rotor Permanent Magnet Brushless Motors with Cylindrical and Disctype Slot－less Stator［D] .Thesis document，Louisiana State University，Baton Rouge，August 2007.

［2] 张凤阁，刘光伟，陈进华.异向旋转双机械口永磁电机磁路建模与场分析［J] .电机与控制学报，2009，13（6）：804－809.

［3] I kariga Atsushi， Shimoji Hiroyasu， Enokizono Masato.Magnetic Characteristic Analysis of Dual－rotor Machines［C] .Proc eedings of the 12th International Symposium on InterdisciplinaryElectromagnetic，MechanicandBiomedical Problems.ISEMBadGastein，2007，173－177.

［4] 何 苗.双转式永磁无刷电动机的控制［J] .微特电机，2009，（11）：26－29.

［5] 张式勤，邱建琪，储俊杰.双转式永磁无刷直流电动机的建模与仿真［J] .中国电机工程学报，2004，24（12）：176－181.

［6] 徐衍亮，王法庆，冯开杰.双转子永磁电机电感参数、永磁电势及齿槽转矩［J] .电工技术学报，2007，22（9）：40－44.

［7] T S No，J E Kim，J H Moon.Modeling，Control，and Simulation of Dual Rotor Wind Rurbine Generator System［J] .Renewable Energy，2009，34（10）：2124－2132.

［8] Fe ngge Zhang， Guangwei Liu，Yongshan Shen，etc.CharacteristicStudyonaNovelPMSMwithOpposite－rotation DualRotors［C] .IEEE International Conference on Electrical MachinesandSystems，Seoul，Oct2007，805－809.

［9] Ronghai Qu，Thomas A Lipo.Dual－rotor，Radial－flux，Toriodally－wound，Permanent－magnet Machines［J] .IEEE Transaction on IndustryApplications，2003，39（6）：1665－1673.

［10] 李练兵，陈 鹏，史广奎.混合动力汽车用双转子电机的建模与仿真［J] .电机与控制学报，2008，12（4）：403－408.

［11] 赵 峰，温旭辉，刘 钧.永磁－永磁型双机械端口电机系统建模［J] .中国电机工程学报，2007，27（21）：59－65.