新一代高速动车组380CL头型与原型车气动特性比较

邓海，夏东伟，尹华，李树民，

(1.中国北车集团 长春轨道客车股份有限公司，吉林 长春 130062;2.中国空气动力研究与发展中心，四川 绵阳621000)*

0 引言

中国北车长客公司在时速300 km/h原型车的基础上，进一步研究时速380 km/h的新一代高速列车，该速度已超过大型飞机的最大起飞速度，且采用多体连接的长大编组结构(最多有16辆车，长度达400 m)，是目前世界上设计的商业运营速度最高、长度最长的高速列车.列车高速运行时，气动效应随速度指数急剧增加，如何有效降低纵向气动阻力、控制气动噪声、提高横向抗侧风能力、抑制气动升力、降低交会压力波和微气压波效应，以确保列车高速运行的安全性、乘坐舒适性、节能环保性和经济性，这对设计具有多方面综合优异空气动力学性能的头型提出了严峻的挑战.

数值模拟、风洞试验、动模型试验、实车测试，是目前研究高速列车空气动力学问题的四个基本手段，其中数值模拟方法，可以模拟最接近实车测试的情况，又可以避免实车测试存在的各种复杂干扰因素，同时数值模拟可以方便的实现流场可视化，可以直观的分析高速列车的流动特性，是高速列车流线化和流线型头型设计、评估、优化的合适手段.

本文采用计算软件PWS3D(Parallel Wind Solver 3D)开展计算，该软件数值求解的控制方程为RANS方程(Reynolds Averaged Navier-Stokes方程)，湍流采用低雷诺数两方程湍流模型，离散方法为有限体积法，求解方法采用压力修正算法［1-2］.

1 数值方法

高速列车尺度大，运行速度高，雷诺数范围在106以上，故对应的流态均为湍流.列车纵向尺度远大于横向尺度，近壁区的处理对边界层发展，压力分布，尾涡强度的准确模拟都非常重要，近壁区网格需要优化配置并充分加密，因此本文采用“雷诺平均N-S方程+低雷诺数两方程湍流模型”的方法进行模拟.

雷诺平均的Navier-Stokes方程的通式可写为［1-3］:

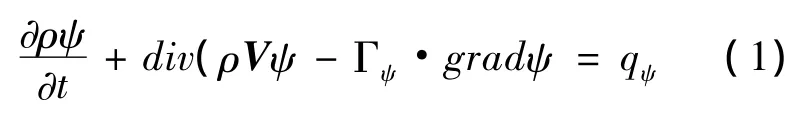
对于连续方程:

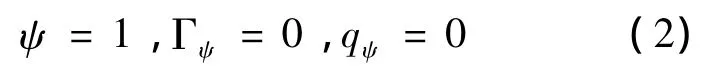
对于x方向的动量方程:

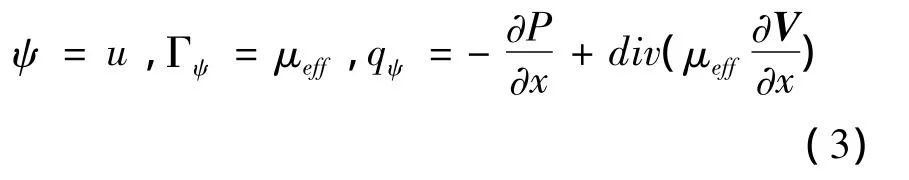
式中，ρ为密度;u为x方向速度;μeff为有效粘性系数;P为压力;V为速度矢量;y、z方向具有类似的表示.

采用两方程模型计算湍流运动.除了求解NS方程的连续方程和动量方程之外，还需求解附加的两个反映湍流运动尺度的方程，即低雷诺数湍动能方程及湍动能耗散率方程，具体可参见文献［4］.

压力系数:

式中，V∞为远场来流速度.

2 计算外形和计算网格

新一代380CL(记为CRH380CL)与原型车(记为CRH3C)外形的区别主要在车头外形和车头转向架裙板，图1给出两车头型的差异(图中深色曲线为 CRH3C，浅色曲线为 CRH380CL)，CRH3C车头鼻锥段长度为7.5 m，CRH380CL车头鼻锥段长度为8.6 m.380CL相对CRH3C主要改进措施为:加大长细比，采用具有旋转抛物体特征的楔形结构，优化头型断面梯度，减小头型过渡区域曲率，截面积变化率更趋线性，合理匹配鼻锥曲面，消除表面凸起，这些措施都可以有效地改进CRH380CL的气动性能.

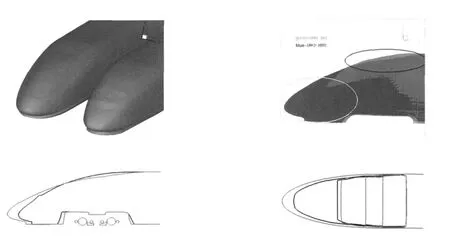
图1 CRH380CL与CRH3C头型比较

除头车外，两车车身部分完全一致，从CRH380CL计算和试验的外形比较可以得到，计算与试验外形完全一致，为突出头型数据，空调、受电弓采用整流罩代替，原型车采用相同处理.

3车编组全区域计算网格由3 000块结构网格组成，总的网格数近5×107.网格在空气动力学数模的基础上生成，动车组3车编组计算区域见图2，无侧滑和有侧滑均采用全区域计算:对模型比例1∶1情况，长度方向远场到车的距离取为66 m，为车横向特征尺度的20倍以上，高度和宽度方向远场到车距离分别为80 m和100 m左右，为车横向特征尺度的25倍和30倍.这样的远场距离可以保证纵向和横向脱落涡的充分发展，用于存在非定常涡脱落的大长细比高速动车组计算是适合的.

图2 动车组3车编组计算区域示意图

图3给出两车车头区域的网格拓扑情况，车头是影响计算结果的重要部位，因此在该区域分布了较密的网格以保形，同时根据流动特点规划分区拓扑结构，以保证模拟精度.图4给出车身连接处，转向架、风档和空调整流罩计算网格，在风挡内车厢连接褶皱区都生成了计算网格，对转向架、风挡等复杂外形结构，采用结构网格非结构化技术，生成了质量较好的多块对接结构网格，以保证复杂外形区域的数值计算精度.在网格分布方面，对曲率变化较大的部分和关键区域都进行了网格加密，以满足此类问题计算对网格的要求，近壁面第一层网格最小网格高度为1 mm.

图3 两车车头网格分布图

图4 车身连接处，转向架、风档和空调整流罩计算网格

3 计算结果及分析

3.1 阻力特性比较

为进行阻力比较，计算了3车编组“光车”的阻力特性，即去掉了空调、受电弓、转向架等部件，采用头型+等直段方案，1∶8模型.由于等直段不贡献任何压差阻力，计算结果中的压差阻力全部来自头型，也就是在理想状况下，CRH380CL的头型构成的头尾车压差阻力会比CRH3C头型减阻23%，3车编组“光车”全车减阻12.8%，这两个结果是理想状态下头型的最大减阻情况.

计算与试验的气动力比较见表1，计算与试验结果吻合较好.表2给出计算阻力系数比较，CRH380CL 3车编组比CRH3C 3车编组减阻4.5%，头、尾车阻力之和 CRH380CL头型比CRH3C头型减阻7.3%，新一代头型减阻效果明显.“光车”和1∶8模型计算与试验结果表明:CRH380CL头型阻力明显小于CRH3C头型，其阻力特性优于原型车.

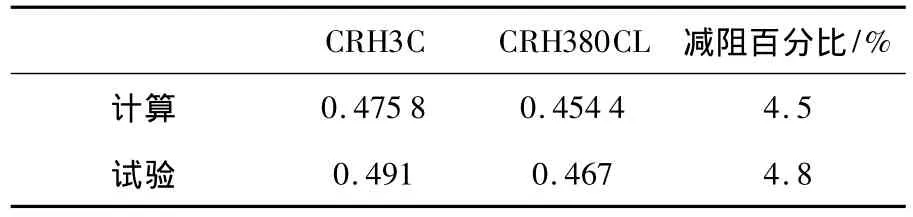
表1 计算与风洞试验阻力系数比较(1∶8模型)

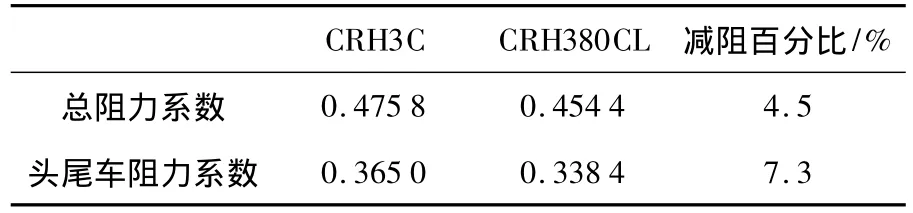
表2 计算总阻力与头尾车阻力系数结果比较(1∶8模型)

图5给出计算的两个车型表面压力云图尾流流线，由于加大了长细比，改进了鼻锥曲线，CRH380CL尾车流动有更好的附着性，是该头型减阻的主要原因.

图5 计算的两个车型表面压力云图尾流流线

3.2 升力特性比较

表3是在固定地面、来流60 m/s，无侧风条件下，两头型对应的头车、尾车升力系数比较，两头型头车均为负升力，即向下的压力，尾车均为正升力，方向向上，对流线型头型，尾车的正升力会导致尾车的摆动，影响尾车稳定性和舒适性，因此，在改进头型设计时，希望尾车升力不要增加，CRH380CL尾车的升力明显小于CRH3C，因此，CRH380CL头型的升力特性也优于原型车CRH3C.

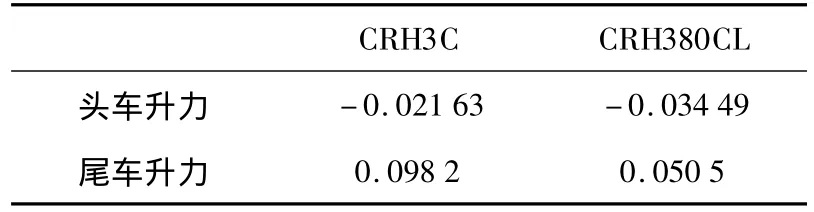
表3 两车型3车编组升力比较(1∶8模型)

3.3 侧力和滚转力矩比较

列车在侧风，特别是大侧风条件下的侧力和滚转力矩特性与列车的安全性直接相关，是头型气动性能比较的一个重要方面，为考察两个头型的抗侧风性能，依据铁运函规定，确定3个侧风工况，记为:

A2:Vtr=300 km/h，侧风 Vw=15 m/s;

A3:Vtr=200 km/h，侧风 Vw=25 m/s;

A4:Vtr=160 km/h，侧风 Vw=30 m/s.

风洞中由于来流速度有限，无法实现以上工况，基于保证两个方向速度相对关系不变的原则，基于风洞能力对风洞的侧风工况进行了调整，对应的1∶8模型风洞试验侧风试验及相应计算工况为:

A2:风速 60 m/s，侧滑角 β =10.2°

A3:风速 60 m/s，侧滑角 β =24.2°

A4:风速 54 m/s，侧滑角 β =34°

表4为在固定地面、风速60 m/s时，不同侧滑角条件下，两头型头车及全车侧力比较以及两头型头车及全车滚转力矩比较，CRH380CL头型的头车及全车侧力和滚转力矩均小于CRH3C头型，CRH380CL头型比CRH3C头型有更好的抗侧风能力.

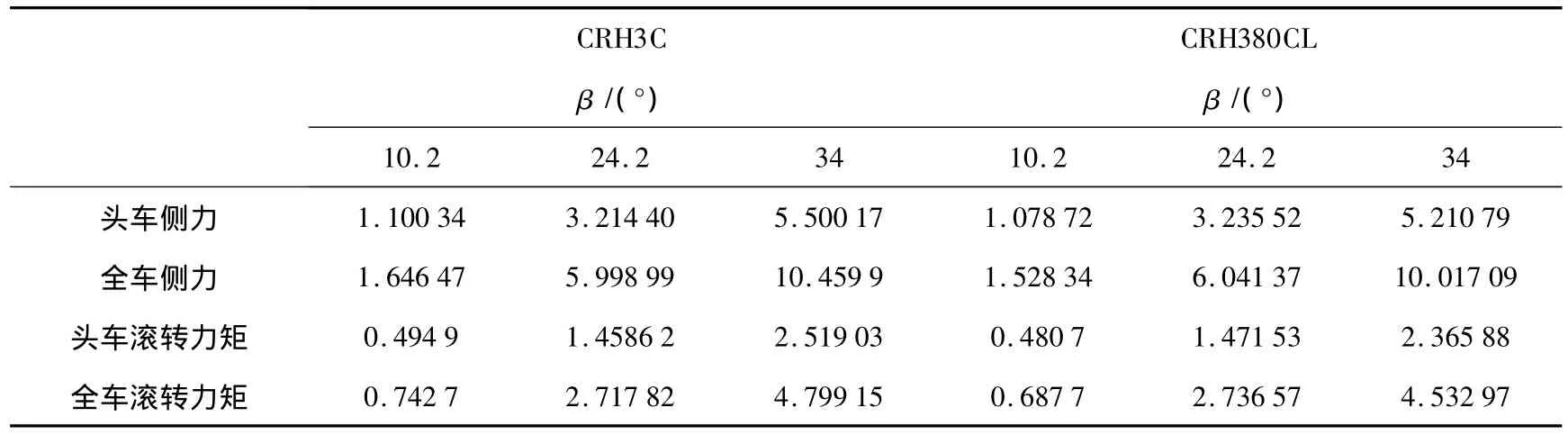
表4 固定地面、风速60 m/s时，不同侧滑角两车型3车编组侧力及滚转力矩比较

3.4 车底优化减阻

CRH380CL-Optimize为在CRH380CL的基础上进行了车底优化，优化方案见图6，采用此优化方案后，3车编组全车减阻达到5.56%，其中头尾车减阻贡献为4.53%，中间车减阻贡献为1.03%，可见车底转向架区域优化的减阻效果是显著的，考虑长大编组情况，每节车有2个转向架，因此，此优化方案对8车和16车编组的情况同样会有显著的减阻效果.图7给出车头转向架区域优化前后外形的比较，以及流动情况，结果表明，通过优化，气流可以更平顺的通过车底，能量损耗少，从而实现减阻，减阻量目前超过头型优化的减阻效果.

图7 车底转向架区域初始外形、优化外形比较

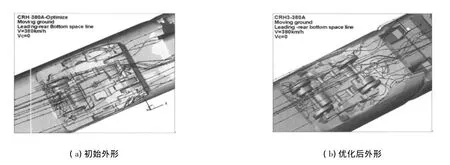
图8 车头转向架区域初始外形、优化外形计算结果比较

4 结论

通过计算研究，CRH380CL和原型车动车组的气动特性，得到如下结论:

(1)380CL相对原型车主要改进措施为:加大长细比，采用具有旋转抛物体特征的楔形结构，优化头型断面梯度，减小头型过渡区域曲率，截面积变化率更趋线性，合理匹配鼻锥曲面，消除表面凸起，这些措施都可以有效地改进CRH380CL的气动性能;

(2)通过对CRH3C头型与CRH380CL头型气动性能的系统比较，包括阻力特性、升力特性、侧力特性、滚转力矩特性和压力波特性，新一代CRH380CL头型全面优于原型车CRH3C;

(3)车底整流效果明显，对3车编组，车底理想化整流减阻极限为全车减阻趋于44%:车底整流类似风挡整流，对长大编组情况应该也有较好的全车减阻效果.

［1］李树民，朱国林，王开春.基于分区的隐式求解二维不可压N-S方程的并行实现［J］.空气动力学学报，2002，20:39-44.

［2］李树民，朱国林，王开春.斜网格修正的低速计算方法及应用［J］.空气动力学学报，2008，26:212-216.

［3］陶文铨.数值传热学［M］.西安:西安交通大学出版社，1986.