基于模糊理论的开关磁阻电机直接转矩控制

王子煜，邓福军

(大连交通大学 电气信息学院，辽宁 大连 116028)*

0 引言

开关磁阻电机(SRM)的双凸极结构和开关式的供电电源模式，是其固有的转矩脉动的根源，严重限制了SRM在工业领域的应用范围［1-3］.因此，转矩脉动抑制方面的研究是当前的热点［4］.众所周知，DTC的独特性在于转矩的直接控制，动态响应很快，且已在感应电机控制应用中获得成功.研究表明，将DTC引入到SRD中，回避了复杂的数学模型的同时，在抑制SRM转矩脉动方面，效果也比较理想，从而获得了较好的转矩、转速控制效果［5］，大大拓宽了SRM的应用市场.传统的DTC技术采用两个滞环比较器来分别控制定子磁链和电磁转矩，其关键在于怎样合理的选择电压空间矢量来实现对磁链以及转矩的控制［6］.而通过滞环来控制磁链和转矩，很难达到理想的性能指标.模糊控制(Fuzzy Control)技术不要求建立精准的系统模型，它通过工程实践，逆向总结出经验规律法则，以此来控制系统，其特性非常适用于SRM的DTC系统.本文将模糊控制技术引入到开关磁阻电机直接转矩控制系统(SRM_DTC)中，以此改进其转矩环节，从而构建出基于模糊逻辑的SRM_DTC系统(SRM_Fuzzy_DTC)，并且在MATLAB/SIMULINK软件环境中对之进行仿真，其波形可以看出，改进后的系统在控制转矩的效果方面明显得到了改善.

1 SRM_Fuzzy_DTC的结构原理

SRM的瞬时转矩可用下式来表达:

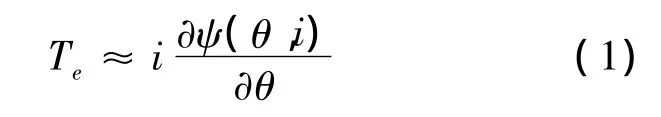
由于SRM单极性的供电结构，由式(1)可看出，电机转矩的正负由的符号决定.

那么，保持定子电流的幅值不变，当定子磁链对电机转子角度的变化率为正时，将之定义为超前转子位置，此时磁链处于加速状态，电机转矩增加;反之，当变化率为负时，定义为滞后电机转子位置，磁链减速，电机转矩减少.并且，在一个微小周期内，控制定子磁链加、减速，此时定子电流会受到一阶延迟的作用，可视其恒定不变.那么，只要改变磁链的加、减速状态，就能达到控制转矩的目的.于是，在SRM_DTC系统中，可通过控制磁链矢量幅值的大小和旋转速度来调节电机的转矩.

当SRM高速运行时，定子电阻的压降影响很小，SRM单相的电压平衡方程可简化为:ΔΨ≈u·Δt，可以看出，定子磁链矢量变化的方向与所加电压矢量方向一致.这样，通过磁链来控制转矩就转化为选择合适的电压空间矢量来控制转矩.

借鉴永磁同步电机DTC系统中模糊控制技术的应用［7］，在SRM_DTC系统中也将两者结合.针对SRM_DTC系统的自身结构，将转矩、磁链偏差用量化因子处理，并映射到相应的模糊集合中，然后判断磁链角所属扇区，由此推导出相应规则，然后经过模糊算法，得到期望的电压矢量，将之解模糊，输出给逆变器.

SRM_Fuzzy_DTC的系统结构如图1所示:

图1 SRM_Fuzzy_DTC系统原理框图

从该系统的原理框图可以看出:

根据实际测得的SRM各相绕组的电压、电流、转子位置角，通过建立的磁链观测模型和转矩观测模型分别估算出其瞬时磁链Ψ和瞬时转矩Te，通过4/2变换，由α-β坐标系中磁链的两个分量得到定子磁链的空间位置角θ.将磁链偏差EΨ、转矩偏差ET和磁链角θ作为模糊控制器的三个输入量，将输出量解模糊后，控制逆变器的开关状态，最终控调节SRM的转矩.其中速度调节器仍采用PID调节器，其输出作为电机转矩的参考给定［8］.

2 模糊控制器的设计

本文中的模糊控制器输入量为模糊化后的磁链偏差EΨ、转矩偏差ET，定子磁链角θ，其表达式如下:

由于定子磁链脉动较小，且不是主要控制目标，故其偏差定义的模糊子集个数相对较少，为:{N，Z，P}，分别代表模糊集合的语言含义为:{负，零，正};而电机转矩是主要控制量，关系到系统性能，且其脉动较大，不易限制，故需要在其论域上细分偏差等级，相应的模糊子集为:{NB，NS，Z，PS，PB}，分别代表模糊集合的语言含义为:{负大，负小，零，正小，正大}.

将定子磁链角均分为12段，并根据SRM与感应电机相数的不同，对其隶属函数曲线做出调整.

输出向量中的每个元素，分别对应SRM每相的电压状态，合成后即为期望的电压矢量.

输入变量的各隶属函数如图2所示:

图2 模糊控制器输入量的隶属函数图

建立模糊规则时，根据输入偏差的等级不同，要选择相应的电压空间矢量，且由于开关表中的电压矢量数目有限，对于磁链、转矩偏差而言，很难同时满足二者的控制要求.那么，在SRM_DTC系统起动初始，磁链偏差很大，为了提高最大转矩的建立速度，需优先满足磁链的控制要求;当磁链的幅值达到给定值后，由于其脉动较小，且较易控制，此时的原则就转为优先满足转矩的控制要求.

在SRM_Fuzzy_DTC系统下，基于模糊理论的DTC规则如附表所示:

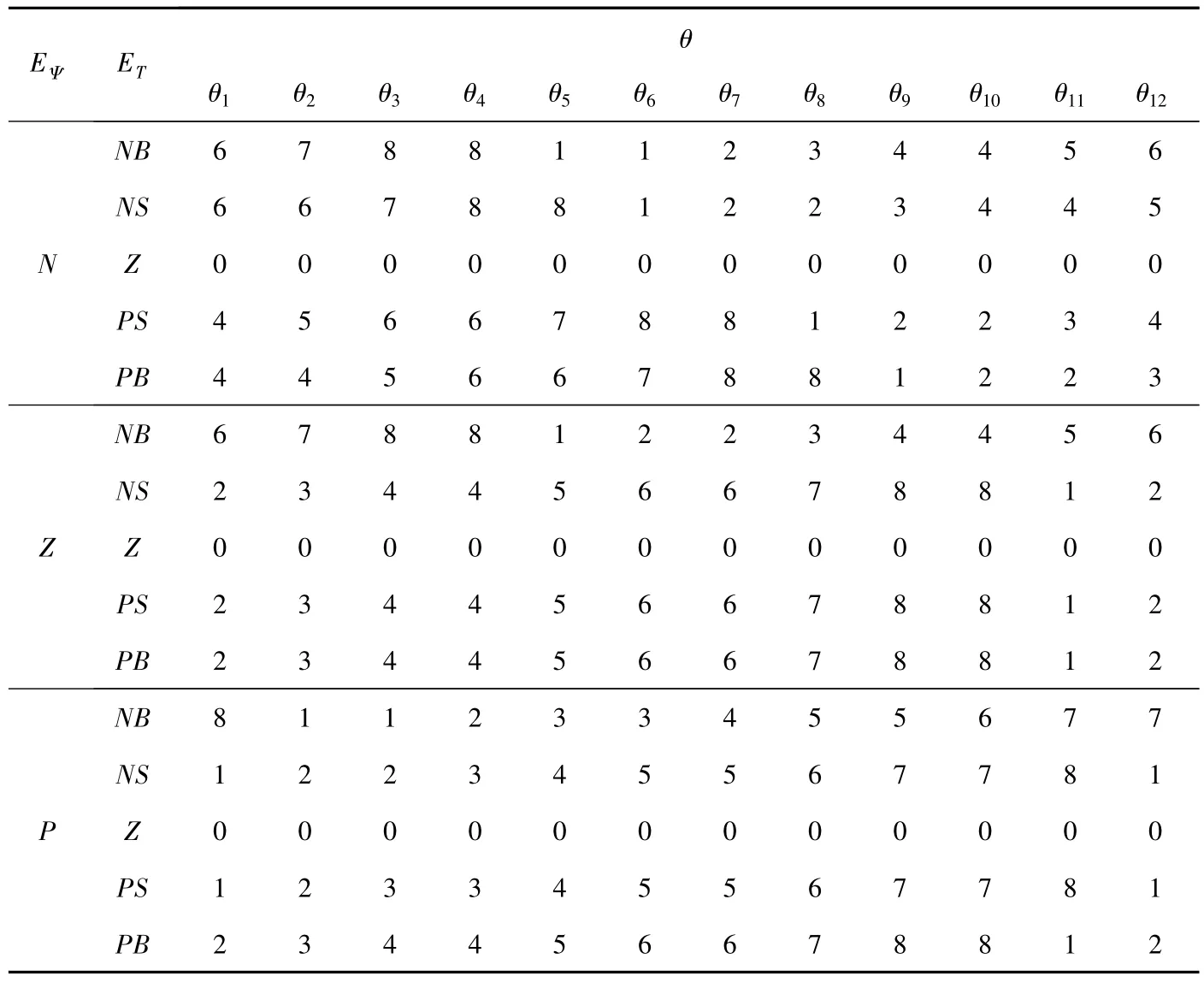
附表 模糊控制规则表

将模糊规则用if-then的形式来表述，则第i条语言为:

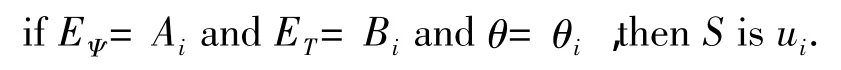
其中，Ai、Bi、θi以及 ui分别为磁链偏差、转矩偏差、定子磁链角以及电压空间矢量的模糊化后的子集变量.

模糊推理采取常用的Mamdani法，第i条控制规则的隶属度ai为:

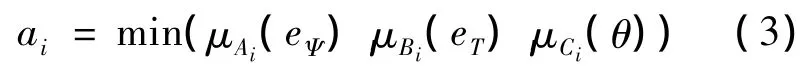
式中，μAi(εΨ)，μBi(eT)，μCi(θ)分别为输入量EΨ，ET，θ的隶属函数.

再取“交”集，得到输出量的隶属函数μVi(S)为:

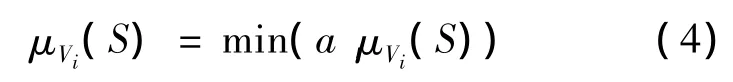
式中，μVi(S)为输出量S的隶属函数.

所有被激活的模糊规则均有各自的μVi(S)，对之取“并”集，则合并后的隶属函数为μV(S):

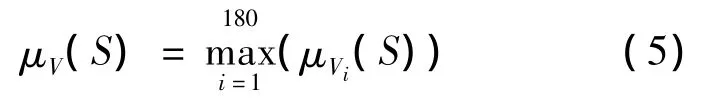
式中，S为基本工作电压矢量.

采用最大值法对μV(S)处理后，即可得到期望的电压空间矢量输出信号.

3 仿真结果及分析

为验证所设计的SRM_Fuzzy_DTC系统的合理性和有效性，采用MATLAB/SIMULINK软件，利用其自带的Fuzzy模块，构建模糊控制器［9］，其输出需经过一定处理后才能控制逆变器，本文中采用S函数的形式构建信号转化模块［10］.对改进后的系统进行仿真，并与SRM_DTC系统作对比分析.

仿真系统的部分参数设定如下:

本系统采用四相8/6极SRM，磁链给定值Ψ*=0.3 Wb，转速给定值 n*=1 400 r/min，SRM空载起动，仿真时间为1 s.

采用传统DTC算法的SRM_DTC系统仿真结果如图3所示.

由图3可以看出，在按照一定规则加在定子绕组上的电压矢量的作用下，定子磁链的幅值保持在滞环容差范围内，近似为圆形轨迹，电机转矩在0.055 s时达到给定值，系统达到稳态，此时转矩在-5～+4 N·m的范围内波动，系统动、静态性能较好.

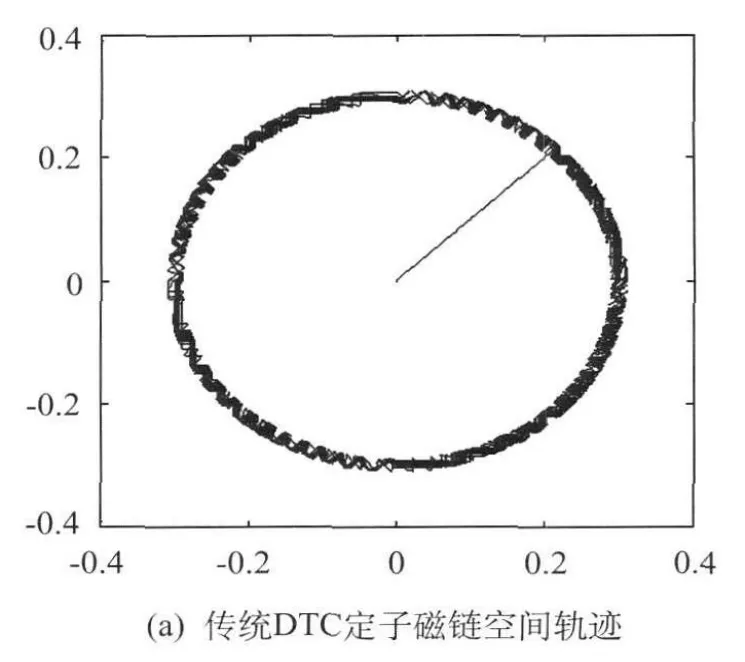
图3 SRM_DTC系统仿真波形

基于模糊逻辑的改进后的SRM_Fuzzy_DTC系统仿真结果如图4所示:

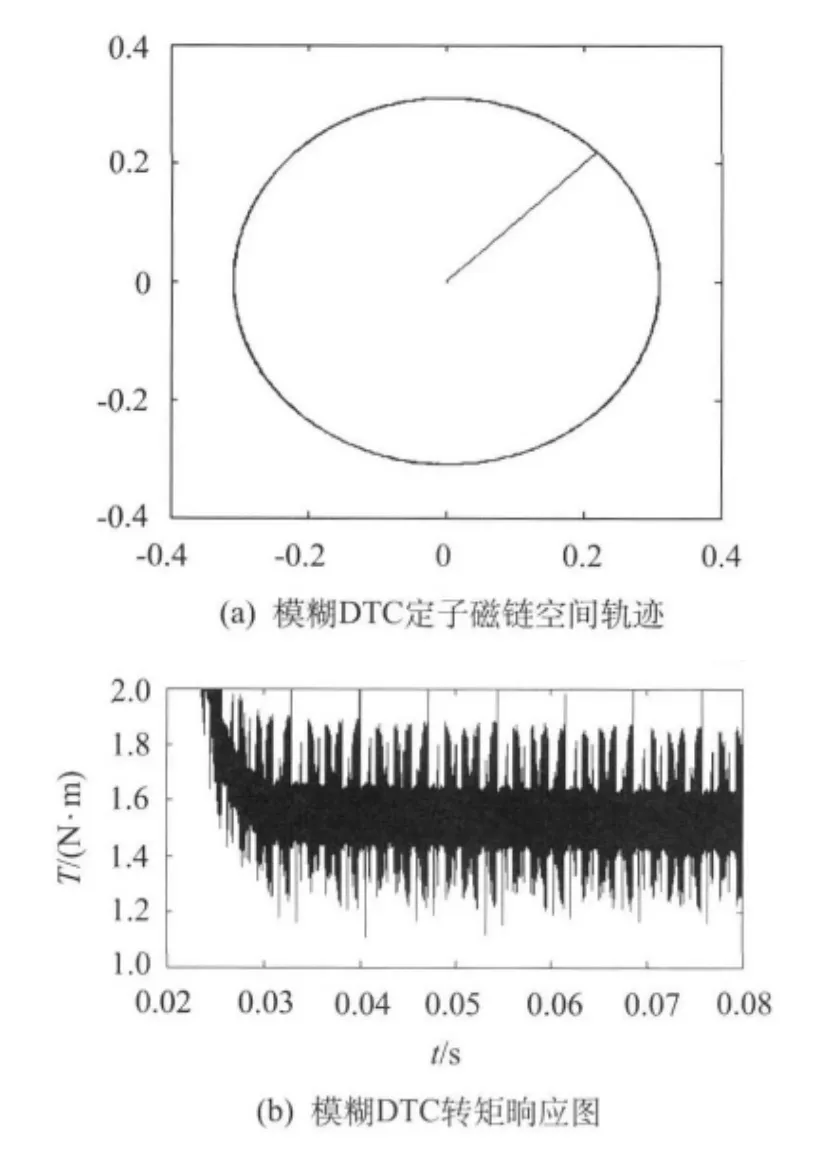
图4 SRM_Fuzzy_DTC系统仿真波形

由图4可以看出，改进后的SRM_Fuzzy_DTC系统，其定子磁链轨迹同样很好的近似达到圆形，且与SRM_DTC系统相比，其滞环宽度较小，表明磁链幅值的脉动较小，对于磁链幅值的控制效果明显更佳，并且在SRM起动时，磁链的幅值呈线性增长，很快达到给定值，加快了电机最大转矩的建立速度，从而优化了系统的动态性能.

而电机的转矩在0.03 s达到稳态，此时转矩在+1～+2 N·m的范围内波动.同SRM_DTC系统相比，SRM_Fuzzy_DTC系统的转矩脉动相对较小，系统的动、静态性能也有了明显提升.

4 结论

本文结合了Fuzzy Control技术和DTC技术，提出了新型的直接转矩模糊控制算法，根据SRM_DTC系统中的磁链偏差、转矩偏差和定子磁链位置角，通过模糊规则，优化选择恰当的电压空间矢量，提高了对电机磁链、转矩的控制效果.与采用传统DTC算法的SRM_DTC系统相比，采用新算法的SRM_Fuzzy_DTC系统转矩脉动较小，而动态响应较快，仿真结果验证了本文提出的新型模糊DTC算法的合理性和有效性.

［1］吴建华.开关磁阻电机设计与应用［M］.北京:机械工业出版社，2000:152-167.

［2］王宏华.开关型磁阻电动机调速控制技术［M］.北京:机械工业出版社，1995:12-20.

［3］KRISHNAN R.Switched Reluctance Motor Drives:Modeling，Simulation，Analysis，Design，and Applications［M］.CRC Press，2001:361-375.

［4］王庆龙，汪增福，张兴，等.SRM转矩脉动抑制的控制策略分析［J］.电气传动，2012，42(2):3-6.

［5］NISAI H FUENGWAEODSAKUL，MARCUS MENNE，ROBERT B INDERKA，et al.High-dynamic Four-quadrant Switched Reluctance Drive Based on DITC［J］.IEEE Trans.Industry Application，2005，41(5):1232-1242.

［6］周扬忠，胡育文.交流电动机直接转矩控制［M］.北京:机械工业出版社，2009:73-98.

［7］孙丹，贺益康，智大为，等.基于模糊逻辑的永磁同步电动机直接转矩控制［J］.电工技术学报，2003，18(1):33-38.

［8］张令霞，张兴华.直接转矩控制系统的Matlab建模与仿真［J］.电气传动，2011，41(1):9-13.

［9］石辛民，郝整清.模糊控制及其MATLAB仿真［M］.北京:清华大学出版社，2008:134-179.

［10］黄志武，刘心昊，年晓红，等.基于Simulink/S函数的直接转矩控制系统仿真研究［J］.自动化技术与应用，2006，25(4):52-56.