基于熵的数据污染率估算*

周访滨 朱建军 陈永奇

1)中南大学地球科学与信息物理学院，长沙 410083

2)长沙理工大学交通运输工程学院，长沙 410004

3)香港理工大学土地测量与地理资讯学系，香港 999077

基于熵的数据污染率估算*

周访滨1，2)朱建军1)陈永奇1，3)

1)中南大学地球科学与信息物理学院，长沙 410083

2)长沙理工大学交通运输工程学院，长沙 410004

3)香港理工大学土地测量与地理资讯学系，香港 999077

提出以熵为计算基础的数据污染率估算方法，避开了传统粗差判别的限差取值问题。数据主体分布模式已知时，利用样本数据估算总体熵和已知主体分布信息估算主体熵获取数据污染前后的熵变化量，通过熵变化率估算数据污染率;数据主体分布模式未知时，通过熵系数计算逼近获取数据主体分布信息，再以熵变化率估算数据污染率。结合熵计算中的截断误差，分析了对污染率的估算影响，数值实验显示，熵计算的截断误差对污染率的估算影响微小，当截断误差达到0.01时，对污染率的估算影响为1%。算例表明基于熵的污染率估算方法有效、可靠。

污染分布;污染率;熵;粗差;限差

1 引言

污染分布研究促进了近代测量误差解析和数据处理理论的发展。Tukey［1］提出的污染分布模式在理论上形象表达了观测数据误差的实际存在状态，其概率密度函数的表达式fC=(1－ε)f+εh，0≤ε≤1中，若不考虑主体分布f和污染分布h的具体表达形式，则污染率ε的大小是衡量数据质量优劣程度的关键指标，但在实际应用中，污染率ε和污染分布h受很多不可知因素制约难于得以显性表达，致使污染分布的研究与应用限于理论分析。近十年来，在数理统计领域有学者致力于应用非参数估计方法研究污染分布中相关参数并进行统计模拟［2－6］，在测量数据处理领域对于污染分布的研究则更多的是抗差估计理论和粗差探测技术［7－11］，对污染率的关注相对较少。污染率是表征观测数据质量好坏的重要指标，确知污染率对粗差探测是一个很好的检核。经典测量数据粗差探测是假设观测误差服从正态分布，以两倍或三倍中误差作为阀值进行粗差统计和剔除，长期统计结果表明，粗差约占观测总数的1%～10%［12］。粗差探测常以标准化残差为参量统计检验观测值是否存在粗差，结果与给定的置信域或显著性水平相关，很大程度上取决于数据处理者的经验和态度。但实际数据误差分布是多样的，有的远离正态分布，若单一依赖标准正态分布的t分位表确定的阀值为限，其局限性明显。笔者认为观测数据被污染必然引起熵的改变，以熵的变化度量数据的污染程度无需过多依赖先验知识，尤其是熵系数可在不作任何假设的条件下严格确定，藉此本研究尝试建立以熵为计算基础的数据污染率估算原理与方法，避开传统粗差判别时限差取值的多元性，利用数据污染前后的熵变率描述观测数据存在的粗差率，分别探讨数据在主体分布模式已知和未知两种情况下的污染率估算方法。以熵为基础估算污染率，熵计算的截断误差不可避免，结合熵计算中的截断误差分析了对污染率的估算影响。

2 基于熵的数据污染率估算方法

2.1 熵的计算方法

熵是信息论中用于度量信源不确定性的唯一量，也是随机性取值不确定性的一种度量。其随机性取值概率越小，相应的熵越大;熵最大，则有最不确定性［13］。一般而言，熵定义为信息量的概率加权统计平均值［14］，熵的计算分为离散型和连续型，即:

当随机变量X取值离散时，其熵H(x)定义为:

当随机变量X取值连续时，

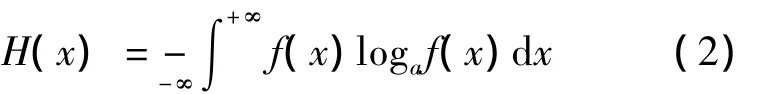
式中，p(xi)为事件的概率，f(x)为概率密度函数。

具有某种概率分布的数据序列，其熵与方差之间存在一定的必然关系。下面推导测量数据处理中常见几种统计分布［15］熵与方差之间的关系。推导中，各分布密度函数均取标准密度函数，且对数取以e为底。

正态分布:

对于P-范分布，由于分布函数相对复杂，根据文献［16］，

P-范分布熵的求解十分复杂，由文献［17］得P-范分布的熵表达式为

2.2 已知数据主体分布模式的污染率估算

依据熵分析一组观测数据可以得到，若该组数据未被污染，其熵值保持恒定;若被污染，其熵值发生改变;如污染加剧，其熵也相应变化加剧，且存在熵变化与观测数据的污染程度存在必然的比例关系。设有一组观测数据li+j(i=1，2，…，n;j=1，2，…，m;n≫m)，定义了li(i=1，2，…，n)为数据的主体部分，而lj(j=1，2，…，m)为数据的污染部分，当m，n无法准确知道时，则不能通过统计粗差的个数计算污染率，但已知li(i=1，2，…，n)的观测误差服从某一确定的分布，一般情况下可以根据经验确定，根据熵的计算原理可以顺利求解其熵H(li)，同样可以求出H(li+j)，则取熵的变化估算污染率ε:

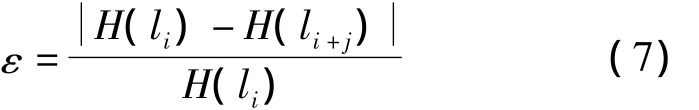
2.3 未知数据主体分布模式的污染率估算

数据主体分布模式已知，实质是利用了先验知识，这需要一定的专业水准和相当丰富的工程经验或科学研究基础，在实际中往往数据主体分布模式是未知的，或者对数据主体分布模式的先验判知不准确，这种情况下基于熵估算污染率的关键是寻求相对准确的数据主体分布模式。在测量数据处理中常见的分布有正态分布、拉普拉斯分布和P-范分布，在这个大前提下，一般的测量观测数据误差分布必然服从或近似服从常见的这三种分布，因此判别数据误差分布模式成为首要问题。本文建议以熵系数做出初步判别，因为一种特定的分布它的熵系数具有唯一性，目前计算得到常见分布的熵系数呈明显规律性，以均匀分布最小，KU=1.732，拉普拉斯分布次之，KL=1.922，正态分布最大，KN=2.066;P-范分布相对特殊，其系数随P值发生变化，其表达式为:

参考已知数据主体分布模式情况下基于熵的污染率估算，若已有一组观测数据li+j(i=1，2，…，n;j=1，2，…，m;n≫m)，其中该数据的主体部分定为li(i=1，2，…，n)，数据的污染部分为li(j=1，2，…，m)，当m，n无法准确知道时，则依赖统计粗差个数计算污染率的方法失效，也未知li(i=1，2，…，n)的观测误差服从某一确定的分布，此时首先应根据熵的计算原理求解熵系数K(li+j)，依据K(li+j)与已知分布熵系数的近似程度估计数据主体部分的分布模式，然后再依照式(7)估算污染率ε。

3 熵计算的截断误差对污染率估算的影响分析

基于熵估算污染率离不开观测数据的熵计算，通常获取的观测数据都是一定量的样本，在计算中必然存在截断误差，样本量的大小会影响污染率的估算，尤其是在未知数据主体分布模式的情况下，通过样本数据熵系数计算判别总体分布将会有影响，文献［18］导出了理论上熵计算最小的截断误差限▽H的表达式如下:

式中，▽H为理论最小熵的计算截断误差限，α是给定微小量，0≤α≤1，D为方差。

同时给出了熵计算的截断误差与给定微小量α(0≤α≤1)之间的对应关系，结果表明α越小截断误差越小。为提高样本熵的计算精度，在实际应用中建议采用全局最优窗宽的理论和算法［18］求解样本熵的估计值。

进一步研究熵计算截断误差对污染率估算的影响程度，采用标准正态分布进行数值演算，假设污染使得原有主体分布的方差膨胀了2倍，得到截断误差与污染率估算的关系如表1。演算结果表明，熵计算的截断误差对污染率的估算影响微小，当截断误差达到0.01时，对污染率的估算为1%。

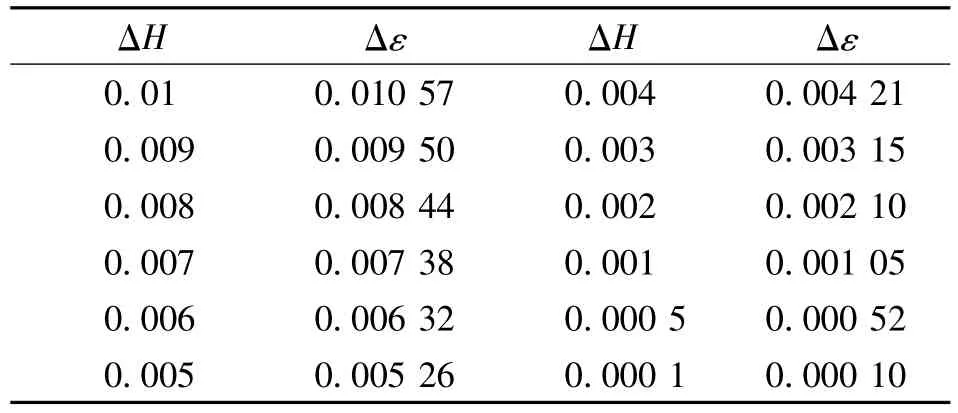
表1 熵计算的截断误差与污染率估算的关系Tab.1 Relation between entropy truncation error and contamination rate estimation

4 算例及分析

算例1，数据取自文献［19］第16页的经纬仪测角实验数据，这些数据服从正态分布，不含粗差，为演算污染率，在已有数据中，设计3种人为加入粗差的方案，方案Ⅰ:人为加入粗差5个，其中超过两倍中误差的2个，超过三倍中误差的3个;方案Ⅱ:人为加入粗差个数等同于方案Ⅰ，误差量较方案Ⅰ减少，其中超过两倍中误差的3个，超过三倍中误差的2个;方案Ⅲ:人为加入粗差6个，其中超过两倍中误差的3个，超过三倍中误差的3个;采用传统方法以两倍中误差及三倍中误差为限统计粗差个数计算污染率，并和基于熵计算结果对比，对比结果见表2。

表2 已知数据主体分布模式污染率ε的估算结果对比(单位:%)Tab.2 Contamination rate ε estimation result of known data main distribution model(unit:%)

表2说明，传统方法以两倍或三倍中误差作为限统计粗差个数计算污染率完全依赖于数据处理者对数据的采信率水平高低，二者之间存在比较大的差异，同时污染率的估算仅与粗差个数密切相关，与粗差个体大小无关，而基于熵的污染率估算避开了粗差统计限差取值问题，计算结果完全不依赖于数据处理者对数据的采信率水平高低，污染率的估算结果不仅与粗差的个数密切相关，而且也反映了粗差个体大小对数据整体的影响。

算例2，数据取自文献［15］中一组大样本GPS RTK观测数据，这些数据通常认为服从正态分布，但蓝悦明［15］分析认为这些数据的分布不能唯一确定，本研究当作未知主体分布模式的例子加以对待，估算其污染率的大小，将平面分量X、Y和高程分量Z分别考虑，采用熵系数方法近似确定数据主体分布模式，估算该组数据的污染率，与传统方法中采用以两倍中误差及三倍中误差为限统计粗差个数计算污染率，分析对比结果如表3。

表3 未知数据主体分布模式污染率ε的估算结果对比Tab.3 Contamination rate ε estimation result of unknown data main distribution model

计算结果说明基于熵的污染率估算可揭示数据观测质量的优劣，以H变化计算的ε十分接近以2σ为限差统计粗差个数计算的ε，表明以熵的变化估算数据污染率可行，亦可靠，它与目前GPS RTK数据观测质量的普遍认知结论是一致的。

算例2的运算结果也说明，当数据的主体分布未知时，采用熵系数计算逼近获取主体分布信息，再以熵变化率估算数据污染率的方法可行。传统方法采用两倍中误差和三倍中误差为限统计粗差个数计算污染率差异明显，当样本数据量增大时，以何种限差剔除粗差更适用取决于数据处理者的经验和态度，若取两倍中误差剔除粗差增加“弃真”的概率，若取三倍中误差剔除粗差增大“纳伪”的风险，如果取用熵估算的污染率为粗差剔除标准，可有效避开粗差阀值的选取问题。

5 结论

1)从熵的角度诠释观测数据的误差成分，以熵变度量数据污染率，避开了传统粗差判别的限差取值问题;

2)基于熵的数据污染率估算必然会受到熵计算中的截断误差影响，分析和数值演算结果表明，当主体分布为标准正态分布时，误差熵计算的截断误差对污染率的估算影响微小，截断误差达到0.01时，对污染率估算的影响为1%;

3)以熵估算污染率不仅与粗差的个数有关，而且与粗差本身的大小有关，说明熵估算对数据误差的敏感性更高，但能否以此进行粗差探测有待进一步研究。

1 Tukey J W.A survey of sampling from contaminated distribution，in:contribution to probability and statistics［M］.Stanford:Stanford University Press，1960.

2 刘红玲，刘建.污染分布的近邻估计［J］.数学杂志，2010，30(1):178 － 182.(Liu Hongling and Liu Jian.Nearest neighbor estimation of contaminated distribution［J］.J of Math(PRC).，2010，30(1):178－182)

3 王丽燕，张奕，冯恩民.污染分布密度函数的一种估计方法［J］.大连理工大学学报，2003，43(5):551 －554.(Wang Liyan，Zhang Yi and Feng Enmin.An estimation method of contamination distribution density function［J］.Journal of Dalian University of Technology，2003，43(5):551－554)

4 杨筱菡.污染分布的非参数估计［J］.同济大学学报，2001，29(6):700 －702.(Yang Xiaohan.Nonparameter estimation of contaminated data［J］.Journal of Tongji University，2001，29(6):700－702)

5 宁静.污染分布的非参数估计及评估数据的统计与修正［D］.中国科学技术大学，2002.(Ning Jing.Nonparameter estimation of contaminated distribution and statistics and correction of assessment data［D］.University of Science and Technology of China，2002)

6 王巍.污染分布非参数推断的研究［D］.复旦大学，1999.(Wang Wei.Study on nonparameter estimation of contaminated distribution［D］.Fudan University，1999)

7 归庆明，等.粗差探测的Bayes方法［J］.测绘学报，2006，35(4):303 －307.(Gui Qingming，et al.Bayesian approach for detection of gross errors［J］.Acta Geodaetica et Cartographica Sinica，2006，35(4):303－307)

8 Gui Qingming，et al.Bayesian Approach for detection of gross errors based on posterior probability［J］.Journal of Geodesy，2007，81:651 －659.

9 李保利，宫轶松，归庆明.基于方差膨胀模型的粗差探Bayes方法［J］.测绘科学技术学报，2007，24(6):399 －401，405.(Li Baoli，Gong Yisong and Gui Qingming.Bayesian approach for detection of gross errors based on variance inflation model［J］.Journal of Geomatics Science and?Technology，2007，24(6):399 －401，405)

10 朱建军.污染误差模型下测量数据处理理论［D］.中南大学，1998.(Zhu Jianjun.The theory of errors and surveying adjustment under contaminated error model［D］.Central South University，1998)

11 李德仁，袁修孝.误差处理与可靠性理论［M］.武汉:武汉大学出版社，2002.(Li Deren and Yuan Xiuxiao.Error processing and reliability theory［M］.Wuhan:Wuhan University Press，2002)

12 周江文，等.抗差最小二乘法［M］.武汉:华中理工大学出版社，1997.(Zhou Jiangwen，et al.Robust least square method［M］.Wuhan:Huazhong University of Science and Technology Press，1997)

13 林洪桦.现代测量误差分析及数据处理［J］.计量技术，1997，(2):39 －44.(Lin Honghua.Modern surveying error analysis and data processing［J］.Measurement Technique，1997，2:39－44)

14 陈丽英.略论信息论在误差理论中的应用［J］.长春邮电学院学报，1999，(2):37 －40.(Chen Liying.Applications of information theory in error measurement［J］.Journal of ChangchunPost and Telecommunication Institute，1999，2:37－40)

15 蓝悦明，王楠.GPS观测值误差分布的研究［J］.测绘通报，2011，(2):6 － 7，13.(Lan Yueming and Wang Nan.The study of probability density function for GPS RTK observations［J］.Bulletin of Surveying and Mapping，2011，2:6 －7，13)

16 孙海燕，潘 雄.一元P-范分布的参数估计［J］.武汉大学学报(信息科学版)，2003，28(5):551－554.(Sun Haiyan and Pan Xiong.Parameter estimation of the mondic pnorm distribution［J］.Geomatics and Information Science of Wuhan University，2003，28(5):551－554)

17 李大军，等.未知分布误差的熵不确定度［J］.测绘通报，2002，(12):5 －7.(Li Dajun，et al.Entropy uncertainty of unknown distribution error［J］.Bulletin of Surveying and Mapping，2002，12:5－7)

18 游扬声，马 力，刘 星.误差熵的估计问题研究［J］.武汉大学学报(信息科学版)，2008，33(7):748 －751.(You Yangsheng，Ma Li and Liu Xing.On estimation of error entropy［J］.Geomatics and Information Science of Wuhan University，2008，33(7):748－751)

19 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉:武汉大学出版社，2003.(Surveying Adjustment Subject Group of Wuhan University.Error theory and surveying adjustment［M］.Wuhan:Wuhan University Press，2003)

致谢 衷心感谢蓝悦明教授提供源数据!

CONTAMINATION RATE ESTIMATION BASED ON ENTROPY

Zhou Fangbin1，2)，Zhu Jianjun1)and Chen Yongqi1，3)
1)School of Geosciences and Info-Physics，Central South University，Changsha410083
2)School of Traffic and Transportation Engineering，Changsha University of Science and Technology，Changsha410004
3)Department of Land Surveying and Geo-informatics，Hong Kong Polytechnic University，Hong Kong999077

An estimation method of contamination rate based on entropy was proposed.It is useful for gross error statistic to avoid limited error selection.Two models of data main distribution were suggested to investigate contamination rate and the estimation methods of contamination rate based on entropy were given out.A numerical simulation was performed to analyze the influence of entropy truncation error on data contamination rate estimation.It is less influence for entropy truncation error to contamination rate estimation based on entropy.When truncation error is 0.01，the variation of contamination rate estimate is only 1%.The examples show that the estimation method of contamination rate based on entropy is reliable and superior to the traditional estimation.

contamination distribution;contamination rate;entropy;gross error;limited error

P207

A

1671-5942(2013)04-0092-05

2013-03-07

国家自然科学基金(41171397);湖南省重点学科建设项目

周访滨，男，1975年生，博士研究生，主要研究方向为大地测量数据处理.E－mail:Arthur1975@126.com