基于RSA算法的文件加密系统设计

姜 楠，金英善，崔晓锋，刘 波，李 禾

(1.大连民族学院计算机科学与工程学院，辽宁大连116605;2.辽宁科技大学 理学院，辽宁鞍山114044)

随着网络和通信技术的飞速进步，网上银行、网上合同、电子签名、网上支付等电子商务应用越来越广泛，基于互联网的电子商务已经成为国际现代商业的最新形式。然而，互联网是一个面向全球用户开放的巨大网络，这使得电子商务交易的风险性和不确定性加大，从而对网络传输过程中数据的安全和保密提出了更高的要求。电子商务要发展壮大，进行电子商务交易的数据和传输的信息的机密性和完整性必须受到保护，交易者的身份必须得到认证，对未被授权的进入应该进行控制［1］，密码学的主要任务就是从理论上和实践上解决这些问题。通过采用密码技术对信息进行编码可以隐蔽和保护需要保密的信息，将数据变成不可读的格式，防止未授权者在这些信息的存储或传输过程中进行篡改、删除、替换等，从而实现消息的机密性、完整性和不可抵赖性，并且使消息的接收者应该能够对消息的来源进行鉴别。

密码学中包括对称密码体制和公钥密码体制两种密码体制，而公钥密码体制在电子商务安全中应用更为广泛。公钥密码体制于1976年由W.Diffie和 M.Hellman 提出［2］，这种密码体制采用了一对密钥，一个是公开的，称之为公钥，另一个是秘密的，称之为私钥。用户要保障私钥的安全，公共密钥则可以发布出去。公钥与私钥是有紧密关系的，但从一个密钥难以推出另一个密钥，用公钥加密的信息只能用私钥解密，反之亦然。公钥密码系统可用于以下三个方面:通信保密、数字签名和密钥交换。具有代表性的公钥体制是RSA体制［3］，其安全性就是基于分解大整数的安全性，是迄今为止理论上最为成熟完善的公钥密码体制，该体制已得到广泛的应用。

RSA加密算法是信息安全课程的一个重要内容，为了使学生能够更好的理解和掌握这个密码体制，设计了一个综合性实验项目“RSA加密算法实验”。该试验既融合了数论和密码学知识，也包括了算法分析和程序设计的知识，通过该实验的设计与编程实现可以培养学生分析问题、解决问题的综合能力，开拓学生的创新意识，提高学生的实践能力和开放意识，使学生获得终身受益的理论功底和科学素养。

1 实验原理

1.1 素数测试算法原理

目前大多数公钥密码体制都基于数学上的难题，RSA密码系统的安全性基于大数分解的困难性。求一对大素数的乘积很容易，但要对这个乘积进行因式分解则非常困难，因此，可以把一对大素数的乘积公开作为公钥，通过扩展欧几里得算法求出私钥，这样利用已知的公开密钥和密文恢复出明文非常困难。

素数是大于1且除自身和1之外没有其他因子的自然数。素数是构成整数的因子，每一个整数都是由一个或几个素数的不同次幂相乘得来的。目前还没有有效的方法可以产生任意大素数，素数的生成通常是随机选择一个奇数n，通过素性检测算法进行素性测试，若n没有通过测试，抛弃n，如果通过了足够次数的测试，则认为n是素数。在自然数n附近，每ln(n)个整数中有一个素数。下面介绍两种素性测试算法。

(1)Solovay-Strassen素性测试算法基本原理

Solovay-Strassen素性测试是一个判定奇整数是否为素数的多项式时间的概率算法，该算法是根据Euler准则进行判定的，并且使用了雅可比函数来测试p是否为素数［4］。

Euler准则:p是奇素数，x∈Qp当且仅当x(p-1)/2≡1modp

(2)Miller-Rabin素性测试算法原理

Miller-Rabin素性测试算法也是一个多项式时间概率算法，是素性检测的常用方法。对待测的大整数n，首先计算k，k是2整除n-1的次数，然后计算m，使得n-1=2km，选择一个随机整数a，1≤a≤ n-1，计算 b=ammodn，然后对n 进行素性检测。对a选取不同的随机数，重复t次这样的测试。如果n都能通过测试，则我们可以断定n不是素数的概率不大于1/4t，如果t取值很大，基本上可以肯定n就是素数［5］。

Miller-Rabin素性测试算法与Solovay-Strassen素性测试算法相比，Miller-Rabin算法的有效性和标准性都要好一些，因而使用的比较广泛。

1.2 RSA算法原理

在RSA算法中，运算都是在集合Z*n={x=x(modn)|x∈Z，n=p·q，gcd(x，n)=1}中进行的，共有φ(n)=φ(p·q)=(p-1)(q-1)个元素，Z*n在普通乘法和模运算下构成一个群［6］。RSA算法既可以用于加密，又可以用作数字签名，并可构造其它的签名方案，是目前最能被人们接受的算法，国际上一些标准化组织都已接受RSA体制作为标准。在电子邮件中广泛采用的PGP(PrettyGoodPrivacy)加密技术就是用RSA算法作为传送会话密钥和数字签名的标准算法来确保电子邮件安全的。RSA算法的安全性是基于数论和计算复杂性理论中的下述论断，求两个大素数的乘积在计算上是容易的，但要分解两个大素数的积求出它的素因子在计算上是困难的。大整数因子分解问题是数学上的著名难题，至今没有有效的方法予以解决，因此可以确保RSA算法的安全性。RSA算法是非常著名的公钥密码算法，是一种分组密码，明文和密文是0到n-1之间的整数，通常n的大小为1024位二进制数。该算法首先要生成密钥，即通过素性测试算法生成两个大素数p，q，计算 n=p×q和欧拉函数 φ(n)，φ(n)是小于n且与n互素的正整数的个数，φ(n)=(p-1)(q-1)。选择 e使得 e大于1与 φ(n)互素，即gcd(e，φ(n))=1 ，解方程 ed≡1modφ(n)，0≤d≤n，其中e和d互为模φ(n)的乘法逆元，已知e可以用扩展欧几里得算法求出d。这样可以把e和n作为公开密钥，d作为私人密钥，然后进行加密。加密时先将消息分成大小合适的数据分组，然后对分组分别进行加密，每个明文分组m的二进制值均小于n。

对RSA算法的攻击主要包括以下几个方法:穷举攻击，数学攻击，公共模数攻击，计时攻击。最基本的攻击是穷举攻击，也就是尝试所有可能的私钥，数学攻击的实质是试图对两个素数乘积的分解，计时攻击也可以用于对RSA算法的攻击，计时攻击是攻击者通过监视系统解密消息所花费的时间来确定私钥。公共模数攻击就是如果同一个消息用两个不同的指数(模数相同)加密，这两个密钥又互素，那么无需任何指数就可以恢复出明文［7］。

2 算法设计

2.1 大素数产生算法

素性检验算法通常都是概率性的，但如果算法被多次重复执行，每次执行时输入不同的参数，算法的检验结果都认为被检验的数是素数，那么就可以比较有把握地认为被检验的数是素数。

2.1.1 Solovay-Strassen算法

Solovay-Strassen素性测试算法使用了雅可比函数来测试p是否为素数。

具体过程如下:

(1)Zn中随机且均匀的产生一个小于p的数a;

(2)计算 gcd(a，p);

(3)如果gcd(a，p)≠1，那么p没有通过素性测试，它是合数;

(4)计算j=a(p-1)/2modp;

(5)计算雅可比符号 J(a，p)，若 j≠J(a，p)，那么p肯定不是素数;若j=J(a，p)，则p不是素数的概率最多为50%［5］。

2.1.2 Miller-Rabin算法

具体过程如下:

(1)选择一个小于p的随机数a;

(2)设j=0且z=ammodp;

(3)如果z=1或z=p-1，则p通过素性检测，可能是素数;

(4)如果j＞0且z=1，那么p不是素数;

(5)设j=j+1，如果j＜b(b是2整除 p-1的次数)且 z≠p-1，设 z=z2modp，然后转(4)，如果z=p-1，则p通过素性检测，可能是素数;

(6)如果 j=b且 z≠p-1，那么 p不是素数［5］。

2.2 RSA加密算法

(1)选两个保密的大素数p和q;

(2)计算n=p×q，φ(n)=(p-1)(q-1)，其中φ(n)是n的欧拉函数值;

(3)选一整数e，满足1＜e＜φ(n)，且 gcd(φ(n)，e)=1;

(4)计算 d，满足 d·e≡1modφ(n)，即 d是 e在模φ(n)下的乘法逆元，因e与φ(n)互素，由模运算可知，它的乘法逆元一定存在;

(5)以{e，n}为公开密钥，d为秘密密钥;

(6)计算 c=memodn，求出明文m对应的密文c;

(7)计算m=cdmodn，求出密文c对应的明文m［5］。

2.3 系统实现框图

在本系统中首先随机选择一个奇数，使用素性检测算法判断选择的数是否为素数，如果是保存，如果不是继续判断。通过大素数算法生成两个大的素数p和q，然后计算这两个素数的乘积n，再计算n的欧拉函数值φ(n)。之后选取一个整数e作为RSA算法的公钥，它必须满足大于1且与φ(n)互素。计算RSA算法中的私钥d，而d是e在模φ(n)下的乘法逆元，可以通过扩展欧几里得算法求出。用RSA算法的公钥e加密信息m得到密文c，用私钥解密密文c得到明文m，然后结束。系统实现流程如图1。

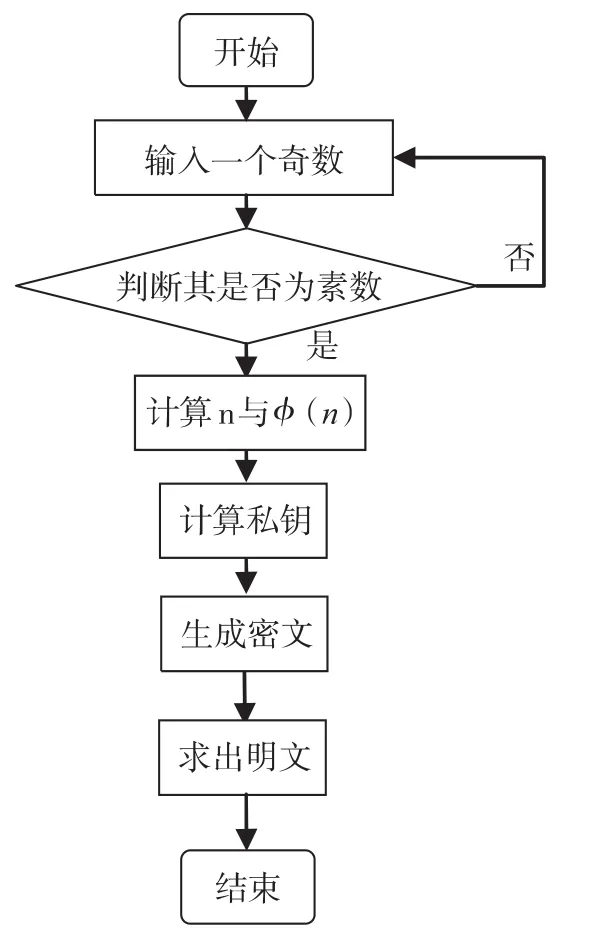
图1 系统流程图

3 结语

RSA公钥加密算法是网络安全技术的重要部分，在身份认证、数字签名和密钥分配等信息安全领域中有广泛的应用。本文主要研究大素数的生成，使用生成的大素数求出RSA算法中的密钥，并且利用该算法进行加密和解密的原理与算法，进而编程实现信息的加密和解密系统。该系统设计的目的不仅使学生掌握公钥密码体制中RSA算法的基本理论，而且能够利用计算机语言编程实现信息加解密程序。通过该算法设计与实现的实验，可以使学生进一步理解书本上学过的密码学理论知识，把抽象知识转化为具体的程序设计，既可以提高学生的学习兴趣，又可以培养学生的算法分析和程序设计能力以及综合分析问题解决问题的能力。

［1］代春艳，谢晓尧，辛明军，等.电子商务信息安全技术［M］.武汉:武汉大学出版社，2007.

［2］DIFFIE W，HELLMAN M E.New directrions in cryptography［J］.IEEE Transaction on Information Theory，1976，22(6):644-654

［3］RIVEST R L，SHAMIR A，ADLEMAN L M.A method for obtaining digital signatures and public-key cryptosystems［J］.Communications of the ACM，1978，21(2):120-126.

［4］孙淑玲.应用密码学［M］.北京:清华大学出版社，2004.

［5］SCHNEIER B.应用密码学［M］.2版.吴世忠，译.北京:机械工业出版社，2000.

［6］司光东，杨加喜，谭示崇，等.RSA算法中的代数结构［J］.电子学报，2011(1):242-246.

［7］SIMMONS G J.A weak privacy protocol using the RSA cryptosystem［J］.Cryptologia，1983，7(2):180-182.