Matlab在求候选关键字的替换算法中的应用

吴荣海，范晓梅

（大理学院数学与计算机学院，云南大理 671003）

候选关键字（candidate keys）在关系模式（relational schema）分解及规范化过程中有重要作用〔1-3〕。但求解给定关系模式候选关键字是NP完全问题〔4〕，很多关系数据库理论工作者提出过求解算法〔4-9〕，但部分文献并未对算法的正确性、完备性给予证明。文献〔4〕给出了一个替换法求解关系模式全部候选关键字算法，并对算法的正确性和完备性进行了证明。文献〔4〕中算法涉及的运算多是集合运算，与VC++、Java等程序设计语言相比，Matlab中的基本数据单元是数组，并提供了多个基于集合运算的函数，从而使繁琐复杂的集合操作变得易于实现〔10〕。文献〔5〕利用Matlab实现了文献〔4〕中算法的M函数，但文献〔5〕给出M函数为了便于计算机实现，对用字符串表示的关系模式上的属性集、函数依赖集事先转换为数值表示，而且实现过程不完全符合文献〔4〕所给算法，后者造成当关系模式函数依赖集不变，属性集个数2倍递增时，所给M函数计算时间呈现指数级增长。本文在文献〔5〕工作的基础上，给出几个改进的M函数，实验表明，本文所给M函数运行时间显著减少，求解正确，结果直观,易于理解。

1 基本概念

关系模式中候选关键字的定义〔11〕如下：给定关系模式R（U，F），U为属性集，F为函数依赖集。

定义1 给定关系模式R（U，F），若∃X⊆U，满足：

则称X为关系模式R（U,F）的候选关键字。

定义3 属性集的闭包〔12〕：给定关系模式R（U,F），设X⊆U，则属性集X关于函数依赖集F的闭包X+定义为

X+={A |A⊆U且X→A可由Armstrong公理导出} 。

定义4 X→Y能由Armstrong公理导出的充分必要条件是Y⊆X+。

2 Matlab中关系模式R（U,F）的描述

一般而言，关系模式属性集、函数依赖集用字符串表示。文献〔5〕为了便于计算机处理，通过建立属性集U{A1,A2,…,An}与1维数组〔1,2,…,n〕的映射关系，即属性Ai对应数组元素i，给出了属性集U、函数依赖集F与Matlab中数值数组、元胞数组（cell array）的一一对应关系。本文采用字符数组与元胞数组结合的办法来建立属性集U、函数依赖集F与Matlab中元胞数组的一一对应关系，这样可以省去转换，也使计算过程更为直观并便于理解。下面以文献〔5〕中所给例子进行说明。

例1 给出关系模式R（U,F），其中属性集U={A,B,C,D}，F={A→BD,CD→B}，X={C,D}。在MATLAB中使用字符数组、元胞数组描述该关系模式如下：

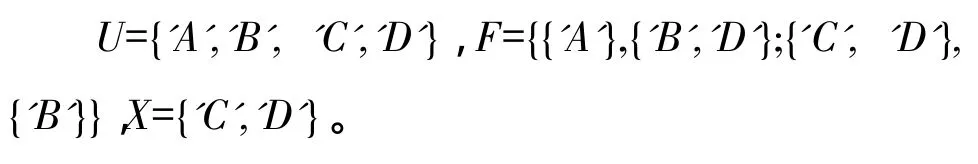
3 算法实现

替换算法〔4〕涉及并、差、包含于、属于等集合运算，在Matlab中可以利用union（）、setdiff（）、ismember（）等函数来实现〔5〕，下面给出算法实现过程中涉及的M函数。

3.1 函数依赖集预处理函数normalizeFDsSet（） 替换算法〔4〕规定关系模式R（U,F）中的F为右部是单属性的非平凡函数依赖集，因此需要对一般的函数依赖集依据函数依赖Armstrong公理进行分解〔5〕。下面给出实现函数依赖集预处理的M函数normalizeFDsSet（）：

function fs2=normalizeFDsSet（FDset）

〔r0,c0〕=size（FDset）;

fs2={};

for i=1:r0

Left=FDset{i,1};

Right=FDset{i,2};

〔r1,c1〕=size（Right）;

for j=1:c1

if～ismember（Right（j）,Left）

fs2=〔fs2;{Left,〔Right（j）〕}〕;

end;

end;

end;

3.2 属性集闭包求解函数attributesSetClosure（） 给定关系模式R（U,F），计算属性集X关于函数依赖集F的闭包X+算法〔12〕简述为：遍历F，如果 ∃Y→Z∈F且Y⊆X，那么X∪Z⇒X，循环迭代结束就可得到X关于F的闭包，记为。实现该算法的M函数attributesSetClosure（）如下。

function cl=attributesSetClosure（X,FDset）

〔r,c〕=size（FDset）;

flag=ones（1,r）;

cl=X;cl0={};

while～isequal（cl,cl0）

cl0=cl;

for i=1:r

if flag（i）&all（ismember（FDset{i,1},cl））

cl=union（cl,FDset{i,2}）;

flag（i）=0;

end;

end;

end;

3.3 去除属性子集冗余属性函数removeRedundantAttributes（） 文献〔4〕给出了一个从给定候选关键字替换出一个新候选关键字的定理并加以了证明，定理如下。

定理1 给定关系模式R（U,F）上的一个候选关键字W，若 ∃B→c∈F,c∉B,c∉W ，令 w1=（W-{c}+B），且执行如下操作：

对于每一个 A→x∈F，只要x∈w1和(w1-{x})→A∈F+，就执行操作(w1-{x})⇒w1，则最终 w1必为关系模式R（U,F）上的一个候选关键字。

由定义4可知，要验证(w1-{x})→A∈F+是否成立，可以验证是否成立，根据定义4和定理1实现去除属性子集中存在的冗余属性的M函数removeRedundantAttributes（）如下：

function ck=removeRedundantAttributes（w,FDset）

〔r,c〕=size（FDset）;

ck=w;

for i=1:r

A=FDset{i,1};

x=FDset{i,2};

if ismember（x,ck）

c=attributesSetClosure（setdiff（ck,x）,FDset）;

if all（ismember（A,c））

ck=setdiff（ck,x）;

end;

end;

end;

3.4 求所有候选关键字函数allkeys（） 文献〔4〕给出推论1并进行了证明，推论如下。

推论1 给定关系模式R（U,F）上的任一个候选关键字W，则可从W出发，导出关系模式上的所有候选关键字。

推论1给出了从一个候选关键字通过替换法导出所有候选关键字的方法，根据定理1和推论1，实现该方法的M函数allkeys（）如下。

function sk=allkeys（w,FDset）

〔r0,c0〕=size（FDset）;

sk={};keys={};w1={};

sk{end+1}=w;keys{end+1}=w;

while ～isempty（keys）

w1=keys{end};

keys（end）=〔〕;

for j=1:r0

if all（ismember（FDset{j,2},w1））

w2=union（setdiff（w1,FDset{j,2}）,FDset{j,1}）;

w2=removeRedundantAttributes（w2,FDset）;

flag=1;

〔r1,c1〕=size（sk）;

for i=1:c1

if isequal（w2,sk{r1,i}）

flag=0;

break;

end;

end;

if flag

keys{end+1}=w2;

sk{end+1}=w2;

end;

end;

end;

end;

4 实例计算

为了便于对比，计算所用例子来自文献〔5〕。

例2 给定关系模式R（U,F），其中属性U={A,B,C,D,G,H}，函数依赖集F={AB→C,C→AB,B→D,D→B,A→G,G→H,H→A}，计算R的全部候选关键字。

上述关系模式R（U,F）以图1所示格式存放为文本文件。

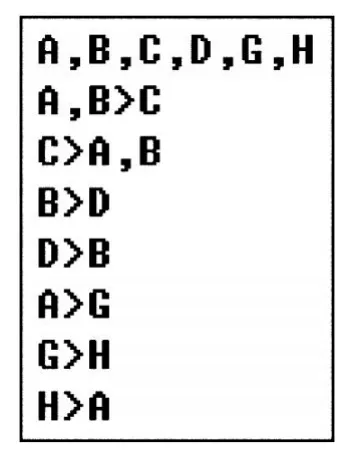
图1 例2所给关系模式R对应的文本文件

图1所示文本文件利用M函数txt2cell（）对其进行读取，并初始化属性集U和函数依赖集F，函数代码如下：

function〔uset,fdset〕=txt2cell（fname）

fid=fopen（fname,'rt'）;

uset={};fdset={};

nline=0;literal='＞';

while feof（fid）==0

tline=fgetl（fid）;nline=nline+1;

if nline==1

〔token,rem〕=strtok（tline,','）;

uset{end+1}=token;

while length（rem）＞0

〔token,rem〕=strtok（rem,','）;

uset{end+1}=token;

end;

else

matches=findstr（tline,'＞'）;

if matches＞0

tmpLeft={};

Left=tline（1:matches-1）;

〔token,rem〕=strtok（Left,','）;

tmpLeft{end+1}=token;

while length（rem）＞0

〔token,rem〕=strtok（rem,','）;

tmpLeft{end+1}=token;

end;

fdset{nline-1,1}=tmpLeft;

tmpRight={};

Right=tline（matches+1:end）;

〔token,rem〕=strtok（Right,','）;

tmpRight{end+1}=token;

while length（rem）＞0

〔token,rem〕=strtok（rem,','）;

tmpRight{end+1}=token;

end;

fdset{nline-1,2}=tmpRight;

end;

end;

end;

下面给出替换算法求解关系模式R（U,F）所有候选关键字的M主函数GetAllCandidateKeys（），函数代码如下：

〔uset,fds〕=txt2cell（‘fds.txt’）;

fds2=normalizeFDsSet（fds）;

ck=removeRedundantAttributes（uset,fds2）;

cks=allkeys（ck,fds2）;

运行上述M函数得到元胞数组cks，如图2所示，从图2中可非常直观地得出关系模式R（U,F）的7 个候选关键字：{D,H}、{B,H}、{D,G}、{B,G}、{A,D}、{C}、{A,B}。该例取自文献〔5〕，但文献〔5〕结果中的{G,B}与{B,G}显然是同一个候选关键字，即文献〔5〕实际得出的候选关键字个数为6个，少了1个{B,H}。

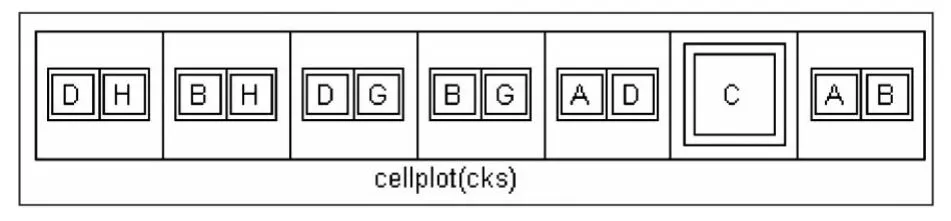
图2 元胞数组cks的结构

本文在PC机上（CPU:Intel Mobile Core 2 Duo T5600,1.83 GHz；内存:DDR2,2 GB,333 MHz），利用MATLAB测试了文献〔5〕所给M函数（记为m1）与本文所给M函数（记为m2）在关系模式R（U,F）函数依赖集不变，属性个数分别为 16、32、64、128、256、512、1024、2048、4096时计算所有候选关键字所需时间。函数m1和m2在每个给定属性个数情况下，各自运行3次，取3次测试结果的平均值，结果如图3。

图3 函数m1和m2求解全部候选关键字所需时间对比

5 结论

从图3可以看出，与文献〔5〕相比，本文所给M函数在函数依赖集不变，属性个数呈2倍递增过程中，计算所需时间增长趋势明显减缓，在属性个数较大（即问题规模较大）的情况下，具有较大优势。

造成差别的主要原因为：文献〔5〕所给M函数OneKey（）在从给定超关键字规约出一个关键字过程（即去除超关键字中存在的冗余属性），实际上是穷举了给定超关键字的所有可能组合，并且每一个组合都需要计算其闭包。这在属性个数增加后所带来的计算工作量是非常大的，因此算法的时间复杂度对属性个数（问题规模）较为敏感。本文所给的M函数removeRedundantAttributes（）是建立在定理1之上，在去除超关键字中存在的冗余属性过程中，只考虑属性依赖集中函数依赖右部包含于给定超关键字的情况，因此算法的时间复杂度对函数依赖集大小较为敏感，而属性个数（问题规模）对算法时间复杂度影响不大，这也与仿真结果相符。

以上M函数均在Microsoft Windows XP Professional Service Pack 3（Build 2600），Matlab 6.5.0.180913a Release 13环境下调试通过。

〔1〕董玉杰,刘海波.基于规范化理论的关系模式优化策略研究〔J〕.北京电子科技学院学报,2010,18（2）:34-40.

〔2〕肖治军,彭小宁.基于特定关系模式下函数依赖集的闭包的研究〔J〕.怀化学院学报,2012,31（5）:27-30.

〔3〕黄灿辉,陈瑛.关系模式规范化算法理论的分析应用〔J〕.现代计算机,2012（31）:12-14.

〔4〕周定康.求候选关键字的替换算法及其正确性和完备性证明〔J〕.计算机学报,1994,17（10）:743-749.

〔5〕胡立辉.MATLAB在求解关系模式上全部候选关键字中的应用〔J〕.计算机应用与软件,2004,21（5）:35-38.

〔6〕冯玉才.候选关键字的求解理论和算法研究〔J〕.计算机应用与软件,1989,6（5）:43-49.

〔7〕Hossein Saiedian,Thomas Spencer.An Efficient Algorithm to Compute the Candidate Keys of a Relational Database Schema〔J〕.The Computer Journal,1996,39（2）:124-132.

〔8〕刘国华,郝忠孝,陈子军.一种求解全部候选关键字的快速替换算法〔J〕.计算机学报,1998,21（10）:890-895.

〔9〕程昌品.一种搜索关系模式的所有候选关键字的算法〔J〕.计算机应用与软件,2005,22（1）:107-108.

〔10〕Stephen J Chapman.Matlab Programming for Engineers〔M〕.Fourth edition.Canada:Thomson Learning,2007.

〔11〕Ullman J D.Principle of Database System〔M〕.Rockville MD:Computer Science Press,1982.

〔12〕刘亚军,高莉莎.数据库基础与应用〔M〕.北京:清华大学出版社,2009:109-143.