基于相位平滑改善信号频谱特性技术研究

赵彦惠

(中国电子科技集团公司第五十四研究所，河北石家庄050081)

0 引言

连续相位调制(CPM)是一类恒包络相位连续的调制方式［1］。由于CPM调制方式的射频信号是包络恒定的，故它对放大器的非线性不敏感，同时射频信号的恒包络性可以大大降低接收端的复杂度［2］。其传输相位在时间上是连续的，带外功率小，临信道干扰小，具有较高的带宽和功率利用率。因此被广泛应用于移动通信和卫星通信领域，在全球通GSM系统中采用的高斯滤波最小频移键控GMSK调制方式即为二进制连续相位调制［3，4］。在传统CPM调制基础上，介绍了一种引入多项式函数实现相位平滑的新方法。

1 连续相位调制

在连续相位调制信号中，信息符号是通过改变载波的相位来发送的，对于所有的符号序列，传输的相位是连续的。CPM传输信号可表示为［5，6］:

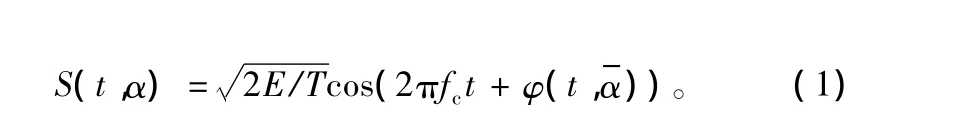
式中，T为符号间隔;E为符号能量;fc为载波频率。α ={α1，α2，α3…}为经过映射的 M 进制数据序列。一般情况下 M∈{2，4，6，8，16…}，αi∈{±1，±3，…，±(M－1)}。对于第n个码元，相位函数为:

式中，h为调制指数;ψ(t)为相应的频率函数g(t)的积分函数，即

2 多项式函数实现相位平滑

2.1 多项式函数模型的建立及求解

下面介绍一种引入了相关性的多项式信号形式，并用这种信号来实现相位轨迹的平滑过程。它可以用多项式f1(t)和f2(t)来表示。在时间区间［0，T/2］内，任何函数都可表示为如下多项式形式:

式中，Bn，n=0，1，2…是多项式的系数，在确定它们的值时，应考虑函数f1(t)存在的边界条件，通过边界条件限制来得到具有优良功率谱特性的信号。相关性的限制条件可表达为如下形式:

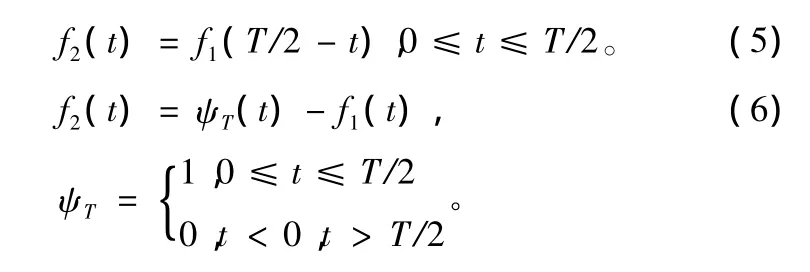
根据信号的相关理论可知，如果时间有限长信号在2个时间端点处满足(γ－1)阶以下的导数都连续，并且γ阶导数处处为有限值的条件下，那么它们的带外功率谱的衰减速度不小于c/fγ+1，c为常数，因此可以说γ决定了所得信号带外功率谱的衰减速度。取边界限制条件f1(0)=0，f1(T/2)=1，为保证函数f1(t)在边界t=0及t=T/2上满足(γ－1)阶导数连续，可得到以下方程组:

则在给定γ值的情况下，可通过建立以下方程组来求解多项式f1(t)中的各项前的系数:

从以上方程组可以得出给定的γ值与最小的多项式幂级数值n满足如下关系，即n=2γ－1。解方程组可得到不同n值条件下f1(t)的表达式:

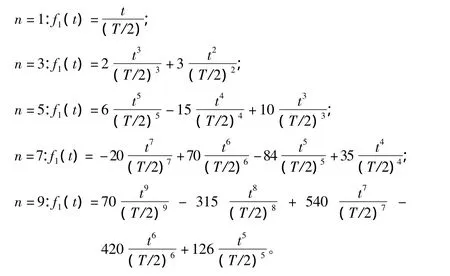
2.2 相位平滑函数的求解

取一个码元周期T的时间内相位变化值为π/2，调制系数为 0.5，即，可以求得在n为不同值条件下的频率调制函数。

取n=5为例，所得曲线如图1所示。

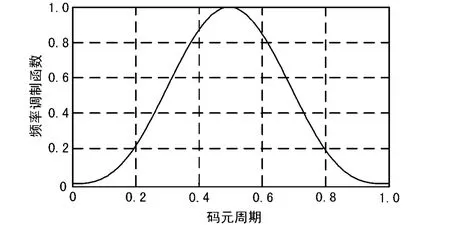
图1 n=5时的频率调制函数gf(t)

根据频率与相位的关系可以得到相位调制函数的表达式ψ(t):

其波形图如图2所示。

图2 n=5时的相位调制函数ψ(t)

在图3中给出了二进制随机序列为0110111100时的相位变化图。

从图2和图3可以看出，相位变化轨迹较平滑，不但保持连续，而且满足码元周期拐点处的高阶导数连续。

图3 二进制随机序列为0110111100时的相位变化

作为比较分析，可以分别得出n=3，7，9时的频率调制函数及相位调制函数的表达式:

2.3 调制方案及频谱分析

可以采用2种正交调制方案实现信号的调制过程。一种为相位波形存储法，即根据所传输的二进制随机信息形成相位信号，再分别乘以正弦及余弦，从而形成基带信号，然后分别乘以正余弦载波信号、相加，最终形成调制信号;另一种方法与MSK信号正交调制的方法类似，即先形成正交调制系统同相信道及正交信道中的基带码元函数，根据所传输的二进制随机信息输出相应的基带码元函数，形成基带信号，然后分别乘以正余弦载波信号、相加，最终形成调制信号。基带码元函数(n=5为例)可表达为如下形式:

其波形如图4所示。

图4 n=5时的基带码元函数曲线

应用MATLB软件计算了所得信号的功率谱密度，并与传统MSK信号的归一化功率谱进行了比较，如图5所示。

图5 归一化功率谱密度曲线

图5中曲线1表示MSK信号［4］的功率谱，曲线2表示n=5时的多项式函数作为相位调制函数时所得信号的归一化功率谱，曲线3表示n=11时的多项式函数作为相位调制函数时所得信号的归一化功率谱。其中，G为所得信号的归一化功率谱。Gs为G(f)在f=0时的值，即Gs=G(0)。

从图5中可看出，在 G/Gs为 －60 dB、n=5、多项式函数U(t)作为正交调制信道的码元函数时，频带宽度为3.7fT，而MSK的频带宽度为7.8fT，减小了2.1倍，比MSK的功率谱衰减速度明显加快，带外信号能量辐射小，即对邻信道信号的干扰小。n=11时的多项式函数作为相位调制函数时所得信号的归一化功率谱相对于n=5时的归一化功率谱的优势体现在－100 dB以下衰减速度明显加快。随n增大，相位调制函数曲线变化更为缓慢，其相位变化轨迹更为平滑了。

3 结束语

提出了一种引入多项式函数实现连续相位调制信号相位平滑的新方法，给出了多项式函数的求解过程。从所给出的相位变化轨迹及归一化功率谱密度曲线来看，所得信号的相位更平滑，在码元周期拐点不但保持连续，而且拐点处的高阶导数仍然保持连续，因此，信号的频谱特性得到了极大的改善，结果证明了该方法的可行性。

［1］何 纬，杜栓义，余 捷.连续相位调制及其捕获技术研究［J］.电子科技，2008，21(3):38 －42.

［2］AULIN T，SUNDERG C E W.Continuous Phase Modulation-part II;Partial Response Signaling［J］.IEEE Trans.Inform.Theory，1981，29(3):210 －225.

［3］马 雯.连续相位调制信号的功率谱及带宽特性研究［J］.现代电子技术，2010(5):38 －41.

［4］孙锦华，李建东，金力军.连续相位调制的非相干减少状态差分序列检测算法［J］.电子与信息学报，2005，27(8):1 338－1 341.

［5］ANDERSON J B，AULIN T.DigitalPhaseModulation［M］.Plenum press，N.Y.，1992.

［6］AULIN T，SUNDERG C E W.Continuous Phase Modulation-part I;Full Response Signaling［J］.IEEE Trans.Inform.Theory，1981，29(3):196－209.