岩石SHPB实验加载过程中应力平衡问题分析＊

平 琦，马芹永，袁 璞

（1.安徽理工大学矿山地下工程教育部工程研究中心，安徽 淮南 232001；2.安徽理工大学煤矿安全高效开采省部共建教育部重点实验室，安徽 淮南 232001）

H.Kolsky［1］建立的分离式 Hopkinson压杆（SHPB）实验装置，在工程领域应用广泛［2－5］，已成为研究高应变率下材料力学性能最基本的一种实验装置。

SHPB实验技术建立在压杆一维应力波假定和试件应力均匀性假定基础之上［6］，由于采用了这2个基本假定，曾引起人们对该实验方法的质疑。20世纪60年代初，E.D.H.Davies等［7］采用能量法对SHPB实验中试件应力均匀问题进行了较为系统的研究，认为试件在满足一定几何特征和加载条件时，应力均匀性假定可以成立，尤其是在金属材料实验中应用效果比较好。

近年来，SHPB实验技术已广泛应用于岩石、混凝土、陶瓷等断裂破坏应变很小的脆性材料［8－11］。SHPB实验中，岩石类脆性材料试件可能在加载尚未结束之前就过早地发生了断裂破坏，导致试件两端应力差异明显，达不到应力平衡，造成实验数据不可靠。试件在断裂破坏之前能否达到应力平衡，已成为评估岩石类脆性材料SHPB实验可靠性的重要标志，再次引起人们的广泛关注［12－17］。因此，有必要对岩石SHPB实验加载过程中试件应力平衡问题做深入探讨，以指导岩石类脆性材料SHPB实验方案的设计。

研究表明［14］，岩石类脆性材料在高应变率下的破坏模式基本上表现为弹／脆性。为简化问题，本文中利用一维应力波理论，采用弹性波讨论SHPB实验加载过程中应力波传播（暂不考虑卸载问题），应适用于弹／脆性破坏的材料或材料的弹性阶段，但对一般材料而言，应力平衡问题主要集中表现在入射加载的前期［13－14］。因此，采用弹性应力波研究分析试件应力平衡等问题，仍具有普遍意义。

1 SHPB实验中应力波传播分析

根据一维应力波理论［6］，应力波在不同波阻抗的介质中传播时，将会在介质交界面上发生透射和反射。SHPB实验中，弹性应力波在压杆和试件中的传播过程如图1所示。

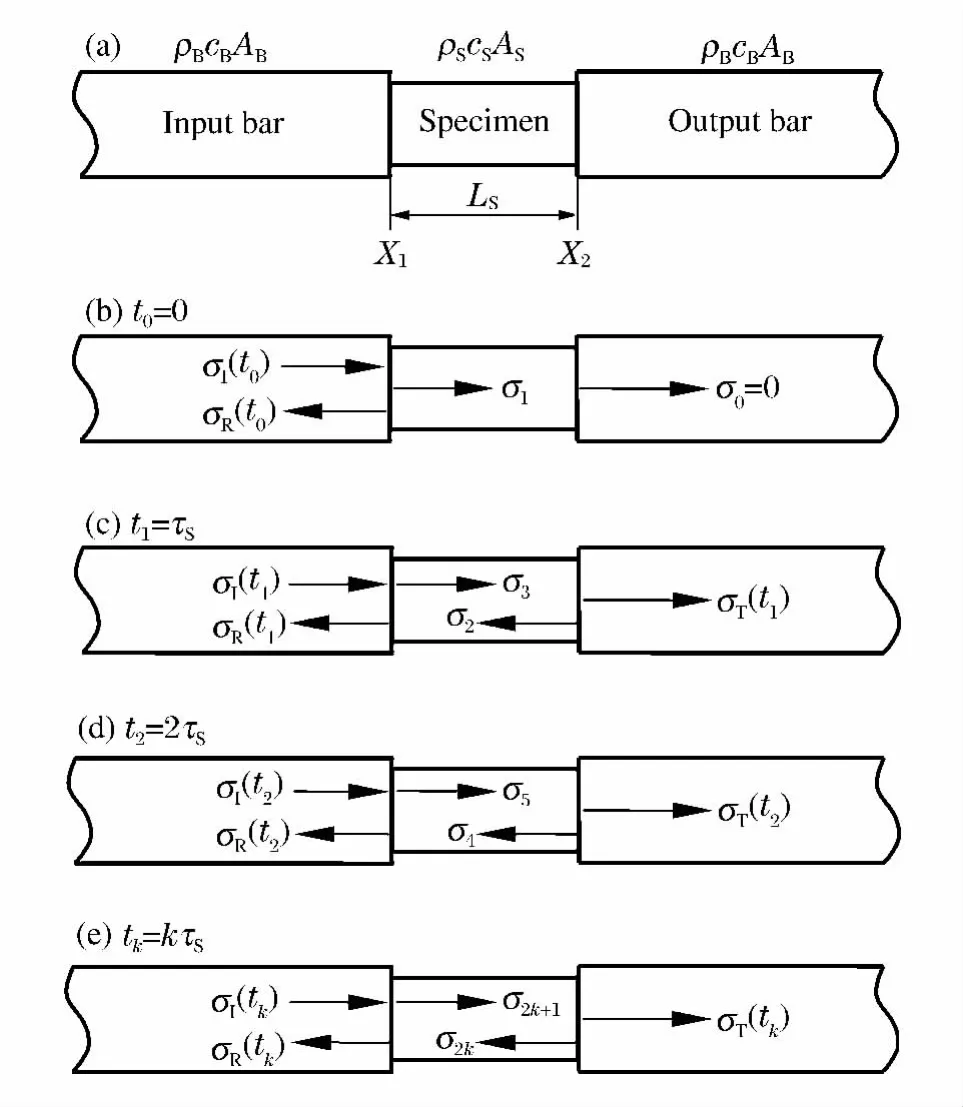
图1 SHPB实验中弹性应力波传播过程Fig.1 Elastic stress wave propagation in SHPB experiment

图1中，σI（t）、σR（t）、σT（t）分别为压杆中的入射应力、反射应力、透射应力。若令α＝AS／AB为试件／压杆的截面积比，β＝（ρScSAS）／（ρBcBAB）为试件／压杆瞬态广义波阻抗比，τS＝LS／cS为应力波从试件一端传至另一端所需时间，则TB，S＝2β／（1＋β）、FB，S＝（β－1）／（1＋β）为试件／压杆的透射和反射因数，TS，B＝2／（1＋β）、FS，B＝（1－β）／（1＋β）为试件／压杆的透射和反射因数。其中，ρS、cS、AS和ρB、cB、AB分别为试件和压杆材料的密度、弹性纵波速和截面积，LS为试件长度。

本文中仅针对α≤1和β≤1的情况进行讨论。设入射加载应力脉冲σI（t）是加载持续时间t的连续函数且有极值。根据应力波理论，并利用线性叠加原理［6，14］，讨论弹性波在SHPB实验中的传播。

当入射杆中入射加载应力波σI（t）到达界面X1时，将会在界面X1处首次发生透射／反射，如图1（b）所示。若应力波全部通过入射杆／试件界面（忽略界面处压杆与试件之间的摩擦，下同），并令此时刻为试件中应力波传播的起始位置（即t0＝0）；此时入射加载应力记为σI（t0），则透射应力波在试件中传播引起的应力扰动为

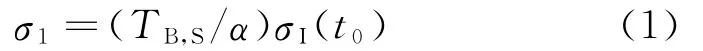
此时透射应力波尚未到达界面X2，故在界面X2处的应力为0，可记为

当经过时间t1＝τS时，如图1（c）所示，试件中传播的透射应力波到达界面X2，在界面X2处发生透射／反射；与此同时，连续变化的入射加载应力波σI（t1）也到达界面X1，将在界面X1处发生透射／反射。此时试件两端的应力状态为

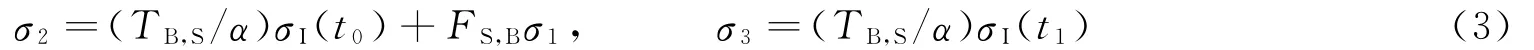
同理，经过时间t2＝2τS时，如图1（d）所示，试件两端的应力状态为

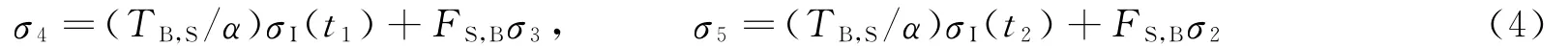
依次类推，当经过时间tk＝kτS时，如图1（e）所示，试件两端的应力状态为

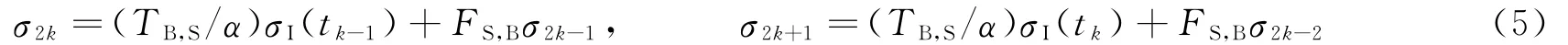
此时，试件两端的应力差和其平均值分别为

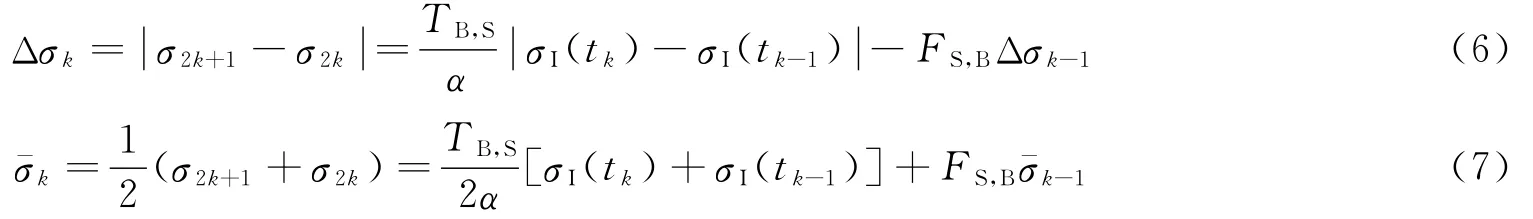
根据牛顿第三定律，可知在压杆／试件界面两侧的力和质点速度应相等，因此可以计算在入射加载任意时刻tk＝kτS入射杆中的反射应力和透射杆中的透射应力，即

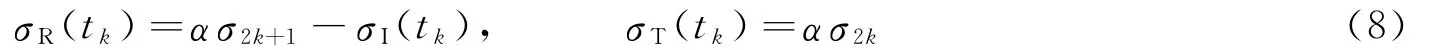
由上述推导计算公式，可进行计算机编程，计算SHPB实验中试件两端的应力、应力差和平均应力，以及压杆中的反射应力和透射应力等相关结果。

2 试件应力平衡影响因素分析

SHPB实验中试件应力平衡程度，通常采用试件两端的相对应力差来进行描述，用试件两端的应力平均值作为试件中的平均应力。即试件的两端应力之差与其平均值之比，则令

式（9）也正是目前普遍比较认同的试件应力均匀性αk的度量方法［6，12，14－15，17］，αk则反映了tk＝kτS时刻试件中的应力平衡程度。显然，αk越接近于0，则说明试件中的应力均匀性越好。

一般近似地认为［12］，当αk≤5%时试件中应力分布达到了应力平衡，即满足应力均匀性假定的要求。因此，可定义满足这一条件时所需的最短时间为试件应力平衡时间tu，则引入量纲一应力平衡时间t′u＝tu／τS。其实，t′u也表示了试件达到应力平衡时应力波在试件中传播的最少次数。

2.1 试件／压杆截面积比α的影响

从式（1）～（5）可以明显看出，试件两端的应力与试件／压杆截面积比的倒数1／α呈线性关系。从式（6）～（9）可以看出，试件应力均匀性αk并不受试件／压杆截面积比α的影响。

因此，试件应力平衡时间t′u可视为与试件／压杆截面积比α无关，因此在后文讨论中将不再考虑α对t′u的影响，令α＝1。实际上，α已隐含于试件／压杆广义波阻抗比β之中，后文将进一步讨论β对t′u的影响。

2.2 入射加载应力幅值σA的影响

从式（9）可以看出，试件应力均匀性αk主要取决于试件两端的应力之差和其平均值，是一个相对比值，因而与入射杆中的入射加载应力幅值σA大小并无直接的关系。

因此，试件的应力平衡时间t′u也可视为与σA无关。故在后文的分析计算中，持续变化的入射加载应力σI（t）可采用量纲一σ′I（t′）＝σI（t′）／σA，其中t′＝t／τS为入射加载持续t的量纲一时间。

2.3 入射加载前沿升时t′r的影响

SHPB实验中，典型的入射波形一般可分为矩形波、梯形波和坡形波［14］。若对这3种波形仅视为入射加载前沿升时的不同，则可统一表示为具有不同前沿升时的梯形波［17］。即升时等于零时，视为矩形波；升时大于感兴趣时段时，视为坡形波；升时介于上述两者之间时，则视为一般意义的梯形波。为便于分析，令t′r＝tr／τS为入射加载前沿的量纲一升时，其中tr为入射加载前沿升时。

根据上述推导计算公式，通过计算机编程计算，得到不同试件／压杆波阻抗比β的试件（β＝1／2、1／4、1／8、1／16），在不同入射加载升时t′r情况下的应力平衡时间t′u变化（t′u－t′r）曲线，如图2所示。

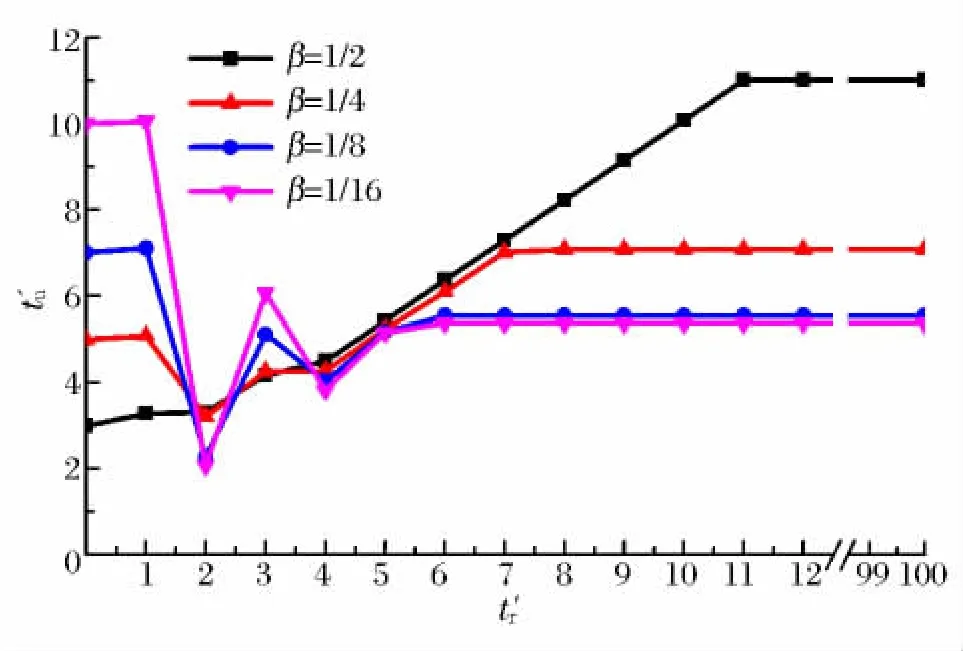
图2 不同波阻抗比试件的应力平衡时间随入射前沿升时变化曲线Fig.2 Relation between time for stress equilibrium and incident rising time at different impedance ratios

从图2可以看出，不同的入射加载升时t′r对不同试件／压杆波阻抗比β试件的应力平衡时间t′u影响规律总体上较为相似。

温室气体的产生和排放是生态系统复杂的生物化学过程。CO2的排放包括植物根系呼吸、土壤微生物呼吸、土壤动物呼吸以及含碳物质的氧化作用，其中土壤微生物的异养呼吸和植物的根系呼吸是土壤呼吸的重要组成 [34]。CH4排放是产甲烷菌及甲烷氧化菌共同作用和传输的综合过程。N2O是通过硝化作用和反硝化作用完成的，该过程离不开微生物的参与[4]。因此，温室气体的产生和排放与土壤微生物是密不可分的[35]。

（1）t′r≤1时，曲线总体上近似为水平线。t′u受t′r影响微弱，仅随t′r增加微量增加，最大增幅也只有8.5%（当β＝1／2时）。因此，t′r≤1时，视为与矩形波（t′r＝0）的情况相同。

（2）1≤t′r≤6时，曲线总体上呈“W”型，变化规律相对比较复杂。曲线簇在t′r＝2、3、4处形成3个明显的拐点，其中t′r＝2为最低点，t′u＝2.1～3.4；t′r＝4也为低点，但并非最低点，t′u＝3.9～4.5；而t′r＝3为高点，t′u＝4.2～6.1。曲线簇在3个拐点的形成过程中，分别在t′r＝1.7、2.3、3.5附近出现了3次交叉，t′u＝3.1～3.8、3.6、4.6；交叉前后，曲线的排列次序依次出现反转。

（3）t′r≥6时，曲线总体上较平，部分曲线已形成水平线。这表明t′u已不再受t′r变化的影响，即在此时后t′u为恒定值。

2.4 试件／压杆波阻抗比β的影响

从图2可以看出，不同试件／压杆波阻抗比β的试件，在相同入射前沿升时t′r情况下，试件应力平衡时间t′u变化规律差异较大。

（1）t′r≤1时，t′u受β影响显著，且β越大，t′u越小。β＝1／2时，t′u＝3.0～3.3，而β＝1／16时，t′u＝10.0～10.1。

（2）1≤t′r≤4时，β越小，t′u变化幅度越大。曲线族在变化过程中出现的2个低点t′r＝2、4和3个交叉点t′r＝1.7、2.3、3.5附近，t′u基本不受β的影响。而在高点t′r＝3为，t′u受β的影响较大。

综上分析表明，试件应力平衡时间t′u受试件／压杆广义波阻抗比β和入射加载升时t′r的影响显著，并不受试件／压杆截面积比α和入射加载应力幅值σA的影响。

其中，有3点应值得注意：（1）若β较大（β≥1／2），应考虑选择t′r≤1（可视为矩形波），则能够获得较短的应力平衡时间；（2）若β较小（β≤1／8），应考虑选择t′r≥6或更大（可视为坡形波）；则能够获得相应的应力平衡时间；（3）不论β为何值，均可考虑选择t′u－t′r曲线在变化过程中出现的2个低点t′r＝2、4和3个交叉点t′r＝1.7、2.3、3.5附近（均可视为常规的梯形波），也能够获得较短的应力平衡时间。且t′r＝2时，应力平衡时间最短，应力均匀性最好。但尽可能避开选择t′r＝3，其应力平衡时间振荡较大。

3 试件应力平衡的有效性分析

入射加载应力幅值σA的大小虽然对应力平衡时间t′u没有影响，但对试件的应变和应变率影响较大。岩石类脆性材料断裂破坏应变εf一般为5‰左右，SHPB实验中试件在断裂破坏之前能否达到应力平衡将直接关系到实验结果是否有效［11，16］。也就是说，必须保证试件达到应力平衡时的应变ε小于断裂破坏应变εf，否则将造成SHPB实验数据不可靠［18－19］，这也正是进行岩石SHPB实验时所要面临和必须解决的问题。

对一次具体SHPB实验来说，压杆和试件的相关参数都是一定的，试件应力平衡时间t′u则完全依赖于入射加载波形。换句话来说，就是在试件／压杆波阻抗比β确定的情况下，试件应力平衡时间t′u的长短完全取决于入射加载升时t′r的变化情况。

根据SHPB实验技术的基本原理，在满足一维应力波假定的条件下，可由试件两端质点速度差与试件长度之比来确定试件应变。经整理，得到常用的三波法公式［6，20］

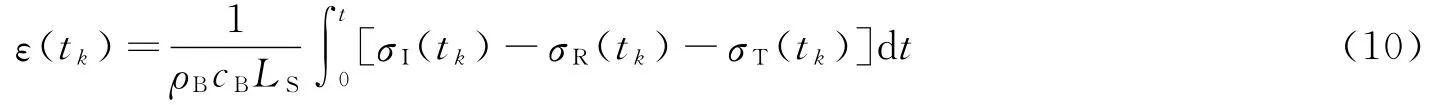
可计算试件在tk＝kτS时刻的应变。

岩石SHPB实验中，压杆若采用直径DB＝50mm 的钢杆（ρB＝7.580g／cm3，EB＝198.646GPa，cB＝5.12km／s），岩石试件（ρS＝2.650g／cm3，ES＝29.5GPa，cS＝3.336km／s）的直径DS＝49mm，厚度LS＝25mm；则α＝0.96，β＝0.218 8，τS＝7.5μs。

以工程应用中常见岩石的抗压强度作为参考，试选取入射加载应力幅值σA＝50、100、150、200 MPa，计算得到不同入射加载升时t′r情况下岩石试件达到应力平衡时间t′u时的应变ε。不同加载应力幅值情况下的（ε－t′r）曲线，如图3所示。

从图3可以看出，入射加载应力幅值σA和入射加载升时t′r均对岩石试件达到应力平衡时间t′u时的应变ε变化影响较大。

（1）入射加载升时t′r相同时，试件达到应力平衡时间t′u时的应变ε随σA的增加而增加。不同σA的ε为倍数关系，即ε∝σA。如t′r＝0时，入射加载应力幅值σA＝50、100、150、200MPa，试件达到应力平衡时间t′u时对应的应变ε＝1.57‰、3.15‰、4.72‰、6.29‰。

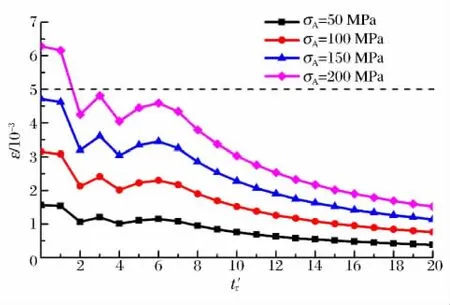
图3 岩石试件达到应力平衡时的应变随入射升时变化情况Fig.3 Relation between strain to stress equilibrium and incident rising time

（2）不同入射加载升时t′r时，不同的入射加载应力幅值σA情况下，试件达到应力平衡时间t′u时的应变ε变化规律极为相似。ε总体上随t′r的增加而减小，且随σA增加，ε－t′r曲线变化幅度明显增大。当t′r≤2时，ε 随t′r增加呈下降趋势。其中，t′r≤1时，曲线下降速度缓慢，近似为水平线；而1≤t′r≤2时，曲线下降速度明显加快。当2≤t′r≤6时，曲线变化呈“N”型。曲线在t′r＝2、3、4、6处形成4个明显的拐点，其中t′r＝2、4为低点，而t′r＝3、6为高点。当t′r≥6时，曲线近似为双曲线形下降，且在t′r≥7后，ε与t′r的倒数（1／t′r）呈现特别显著的线性关系，即ε ＝15.183／t′r（R2＝1）。

（3）入射加载应力幅值σA控制在一定范围内（如σA≤150MPa时），试件在应力平衡时间t′u时的应变ε可不考虑入射加载升时t′r的影响，即t′r无论为何值时，t′u时的ε均在5‰以内。若入射加载应力幅值σA较大，如σA＝200MPa，当t′r＜2时，t′u时的ε已超过5‰，也就是说试件在未达到应力平衡以前就发生断裂破坏，此时的实验数据也将因未能达到应力均匀性基本假定而丧失有效性；而当t′r≥2时，t′u时的ε也在5‰以内。

上述分析表明，要降低试件达到应力平衡时间t′u时的应变ε，采取适当降低入射加载应力幅值σA或提高入射加载升时t′r的控制方法可以实现。岩石材料SHPB实验方案设计中，要保证试件断裂破坏发生在试件达到应力平衡之后，就必须要保证试件在应力平衡时间t′u时的应变ε小于破坏应变εf，SHPB实验所测的岩石类脆性材料的动态应力强度应是可靠的。

4 结 论

（1）试件应力平衡时间t′u受试件／压杆波阻抗比β和入射加载升时t′r影响显著，而不受试件／压杆截面积比α和入射加载应力幅值σA的影响。不同β的试件，t′u随t′r的变化规律较为相似。即，t′r≤1时，曲线为近似的水平线；t′r≥6时，曲线总体上为水平线，这说明在t′r≤1或t′r≥6时t′u对t′r不敏感；而在1＜t′r＜6时，曲线呈“W”型，则表明t′u受t′r的变化影响相对比较复杂。

（2）对β较大（β≥1／2）的试件，可采用t′r≤1（视为矩形波）的入射波加载，则能获得较短的应力平衡时间；而对β较小（β≤1／8）的试件，可采用t′r≥6（视为坡形波）的入射波加载，则能获得相应的应力平衡时间；不论β为何值时，均可采用t′r＝2、4或t′r＝1.7、2.3、3.5（均视为一般意义的梯形波）的入射波加载，则能获得较短的应力平衡时间。其中，采用t′r＝2时试件的应力均匀性最好，应力平衡时间最短。但尽量避开选择t′r＝3。

（3）入射加载升时t′r相同，试件达到应力平衡时间t′u时的应变ε随入射加载应力幅值σA的增加而增加，不同σA加载时的ε成倍数关系，即ε∝σA。ε的变化曲线总体上是随t′r的增加而减小，且随σA增加曲线变化幅度增大。t′r≤2时，曲线呈下降趋势；2＜t′r＜6时，曲线变化呈“N”型，在t′r＝2、3、4、6处形成4个明显的拐点，其中t′r＝2、4为低点，而t′r＝3、6为高点。t′r≥6时，曲线近似为双曲线形下降，且在t′r≥7后，ε与t′r的倒数呈现特别显著的线性关系。

（4）入射加载应力幅值σA过大时，岩石类试件可能未达到应力平衡以前就发生断裂破坏，导致实验数据失效。若要降低试件的应变值，可考虑采取适当降低入射加载应力幅值σA或提高入射加载升时t′r的控制方法来预以实现。SHPB实验中，要保证所测岩石类脆性材料的实验结果可靠，则必须要保证试件在应力平衡时间t′u时的应变ε小于破坏应变εf。

［1］Kolsky H.An investigation of the mechanical properties of materials at very high rates of loading［J］.Proceedings of the Physical Society：B，1949，62（11）：676－700.

［2］胡时胜.Hopkinson压杆实验技术的应用进展［J］.实验力学，2005，20（4）：589－594.Hu Shi－sheng.The application development of experimental technique of Hopkinson pressure bar［J］.Journal of Experimental Mechanics，2005，20（4）：589－594.

［3］Ma Qin－yong.Experimental analysis of dynamic mechanical properties for artificially frozen clay by the split Hopkinson pressure bar［J］.Journal of Applied Mechanics and Technical Physics，2010，51（3）：448－452.

［4］Field J E，Walley S M，Proud W G，et al.Review of experimental techniques for high rate deformation and shock studies［J］.International Journal of Impact Engineering，2004，30（7）：725－775.

［5］代仁平，郭学彬，宫全美，等.隧道围岩爆破损伤防护的霍普金森压杆试验［J］.岩土力学，2011，32（1）：77－83.Dai Ren－ping，Guo Xue－bin，Gong Quan－mei，et al.SHPB test on blasting damage protection of tunnel surrounding rock［J］.Rock and Soil Mechanics，2011，32（1）：77－83.

［6］王礼立.应力波基础［M］.2版.北京：国防工业出版社，2010：5－64.

［7］Davies E D H，Hunter S C.The dynamic compression testing of solids by the method of the split Hopkinson pressure bar［J］.Journal of the Mechanics and Physics of Solids，1963，11（3）：155－179.

［8］平琦，马芹永，张经双，等.高应变率下砂岩动态拉伸性能SHPB试验与分析［J］.岩石力学与工程学报，2012，31（增刊1）：3363－3369.Ping Qi，Ma Qin－yong，Zhang Jing－shuang，et al.SHPB test and analysis of dynamic tensile performance of sandstone under high strain rate［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31（suppl 1）：3363－3369.

［9］王斌，李夕兵.单轴荷载下饱水岩石静态和动态抗压强度的细观力学分析［J］.爆炸与冲击，2012，32（4）：423－431.Wang Bin，Li Xi－bing.Mesomechanics analysis of static compressive strength and dynamic compressive strength of water－saturated rock under uniaxial load［J］.Explosion and Shock Waves，2012，32（4）：423－431.

［10］苏碧军，王启智.Hopkinson压杆对准脆性材料的动态力学实验研究［J］.岩土力学，2003，24（增刊）：580－584.Su Bi－jun，Wang Qi－zhi.Experimental study of dynamic mechanical properties for quasi－brittle materials using the split Hopkinson pressure bar［J］.Rock and Soil Mechanics，2003，24（suppl）：580－584.

［11］朱珏，胡时胜，王礼立.率相关混凝土类材料SHPB试验的若干问题［J］.工程力学，2007，24（1）：78－87.Zhu Jue，Hu Shi－sheng，Wang Li－li.Problems of SHPB technique used for rate－dependent concrete－sort materials［J］.Engineering Mechanics，2007，24（1）：78－87.

［12］周风华，王礼立，胡时胜.高聚物SHPB试验中试件早期应力不均匀性的影响［J］.实验力学，1992，7（1）：23－29.Zhou Feng－hua，Wang Li－li，Hu Shi－sheng.On the effect of stress nonuniformness in polymer specimen of SHPB tests［J］.Journal of Experimental Mechanics，1992，7（1）：23－29.

［13］徐明利，张若棋，张光莹.SHPB实验中试件内早期应力平衡分析［J］.爆炸与冲击，2003，23（3）：235－240.Xu Ming－li，Zhang Ruo－qi，Zhang Guang－ying.Analysis of early stage specimen stress equilibrium in SHPB experiment［J］.Explosion and Shock Waves，2003，23（3）：235－240.

［14］宋力，胡时胜.SHPB测试中的均匀性问题及恒应变率［J］.爆炸与冲击，2005，25（3）：207－216.Song Li，Hu Shi－sheng.Stress uniformity and constant strain rate in SHPB test［J］.Explosion and Shock Waves，2005，25（3）：207－216.

［15］Yang L M，Shim V P W.An analysis of stress uniformity in split Hopkinson bar test specimens［J］.International Journal of Impact Engineering，2005，31（2）：129－150.

［16］朱珏，胡时胜，王礼立.SHPB试验中粘弹性材料的应力均匀性分析［J］.爆炸与冲击，2006，26（4）：315－322.Zhu Jue，Hu Shi－sheng，Wang Li－li.Analysis on stress uniformity of viscoelastic materials in split Hopkinson bar tests［J］.Explosion and Shock Waves，2006，26（4）：315－322.

［17］毛勇建，李玉龙.SHPB试验中试件的轴向应力均匀性［J］.爆炸与冲击，2008，28（9）：448－454.Mao Yong－jian，Li Yu－long.Axial stress uniformity in specimens of SHPB tests［J］.Explosion and Shock Waves，2008，28（9）：448－454.

［18］Frew D J，Forrestal M J，Chen W.Pulse shaping techniques for testing brittle materials with a split Hopkinson pressure bar［J］.Experimental Mechanics，2002，42（1）：93－106.

［19］陶俊林，田常津，陈裕泽，等.SHPB系统试件恒应变率加载实验方法研究［J］.爆炸与冲击，2004，24（5）：413－418.Tao Jun－lin，Tian Chang－jin，Chen Yu－ze，et al.Investigation of experimental method to obtain constant strain rate of specimen in SHPB［J］.Explosion and Shock Waves，2004，24（5）：413－418.

［20］周子龙，李夕兵，岩小明.岩石SHPB测试中试样恒应变率变形的加载条件［J］.岩石力学与工程学报，2009，28（12）：2445－2452.Zhou Zi－long，Li Xi－bing，Yan Xiao－ming.Loading condition for specimen deformation at constant strain rate in SHPB test of rocks［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（12）：2445－2452.