约束条件下多运动体位置跟踪鲁棒控制算法研究

孟 长，胡 磊，魏婷婷

(电子科技大学航空航天学院，成都611731)

1 引言

近年来，作为多智能体协同控制的基础，多智能体一致性跟踪问题的分布式控制一直是控制领域的研究热点［1-2］。文献［3］考虑了智能体之间的通信具有的时延特性和互相干扰的情况。对于干扰，文献［4］中提出了一种通过反馈对干扰进行补偿的方法，文献［5］和［6］详细论述了利用干扰估计器抑制干扰，而文献［7］将干扰估计器应用到一致性的问题中，却没有考虑执行器饱和的情况，也没有给出干扰估计器参数的选择对控制输入的影响。

对实际工程系统来说，所有的执行机构都存在物理约束。在设计控制系统时，必须考虑有界的控制输入对闭环系统性能的影响。如果不考虑这种约束来设计控制律，就很容易出现事故。另外，燃料的使用会使智能体的质量产生小幅度的改变从而改变对象特性，比如［8］中的火箭对接的重负载问题，加上外界不确定力或力矩的干扰，导致智能体的控制愈发困难。而控制器的设计中多使用位置传感器和速度传感器，这样不仅加大了智能体的投入成本，同时引入了更多的干扰，因此提出一种无速度反馈并能抑制这些不确定因素的控制算法就变的很有意义。

本研究通过提出一种控制方案重点解决以下问题:1)在无速度反馈但存在干扰的情况下，结合干扰估计器提出一种有界的位置跟踪算法;2)当执行器饱和值给定时，如何具体设置各项参数以满足这种限制。

2 问题阐述

2.1 背景知识

2.2 数学模型和目标阐述

假设某个组队由n个智能体组成，每个智能体的数学模型都是如下的双积分模型:

其中，i∈In，ui∈R为第i个智能体的控制输入，ri∈R，vi∈R分别代表第i个智能体的位置和速度。所谓一致性位置跟踪分布控制就是对于任意一个智能体，如何设计其控制输入ui∈R，以使得所有的智能体的位置信息最终达到一致，即是说当t→∞时，ri(t)→rj(t)→rd(t)，其中rd(t)为参考位置信号。

本文将考虑两个影响因素:质量变化和外界干扰。质量变化可以理解为，智能体燃料的变化所引起的智能体总质量的小幅抖动;外界干扰理解为智能体所受到的外界不确定干扰，数学模型作如下表述:

其中，i∈In，μi∈R表示第i个智能体的控制输入，mi为质量常量，Δmi和Δfi分别表示质量低频的小扰动和外界的未知干扰信号。为了分析的简单性，令mi=1，整理式(2)，得到:

3 控制算法的设计

3.1 稳定器设计

当di=0时，即针对模型(1)，类比于［9］中提到的控制律，作如下改变:

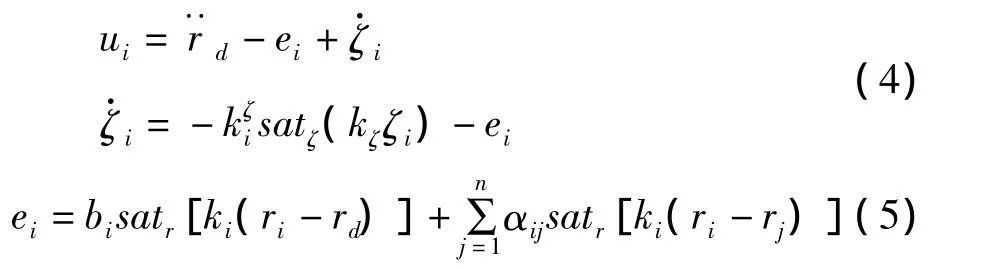
其中，，kζ，ki都是正实数，当第i个智能体能够获得参考信号的信息时，bi＞0;否则，bi=0。

定理1:对于模型(1)，应用算法(4)，假设，1)无向图G是连通的;2)至少有一个智能体可以获得参考信号的信息;3)参考信号的一阶导数和二阶导数和，存在且有界。如果参数k和ibi满足下述关系:

本工程现已运行1年多的时间，运行过程中，尚未发现地表隆起、桩的变形，周边地基土变形等现象，目前使用正常，表明本方案的合理性。

显然，V大于零且无界。分别对其求时间的导数，得到下列关系式:

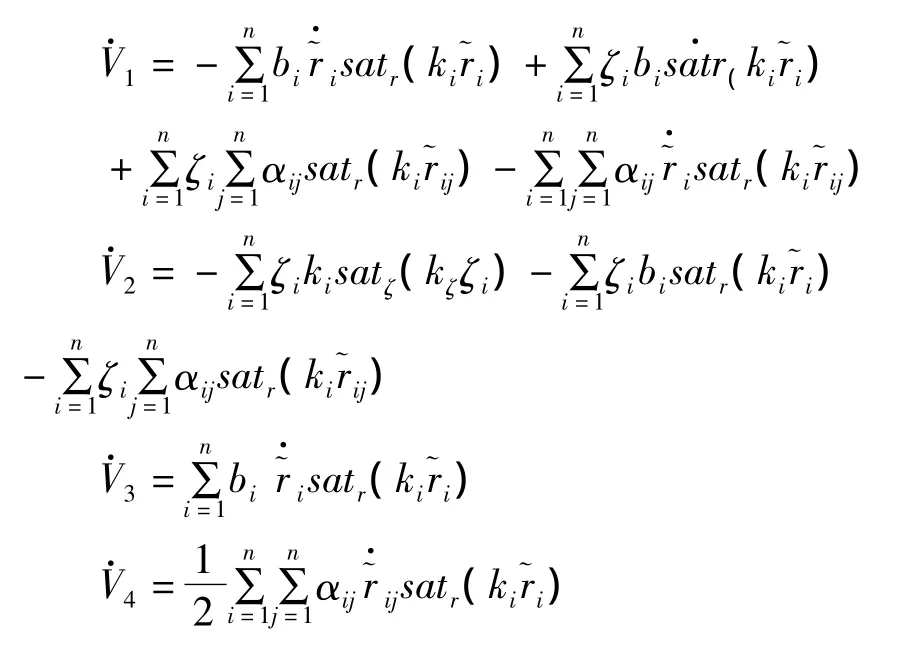
由文献［10］中的引理3.1进一步得到

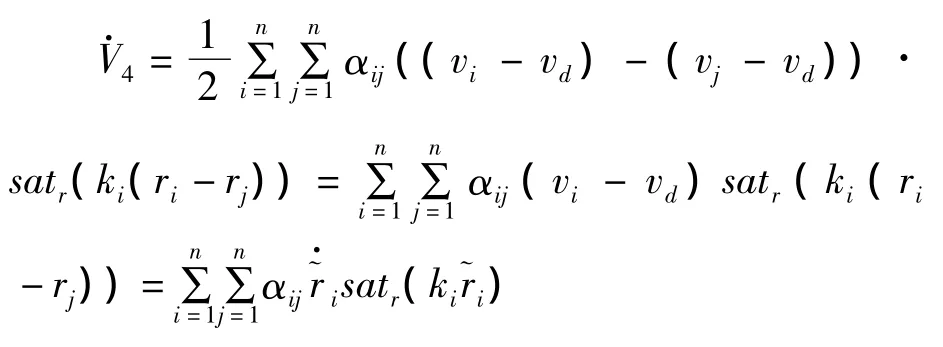
当di不为零时，针对模型(3)，在控制算法(4)的基础上，利用干扰估计器估算出干扰信号的估计值，从而在控制算法里进行补偿，利用这种思想设计如下控制算法:

其中，ui为算法(4)所示的理想模型的控制算法为di的估计值，根据干扰估计器的原理，的拉普拉斯表达式满足下列关系式=Q×di=Q(-μi)。根据式(4)和(7)，进一步得到

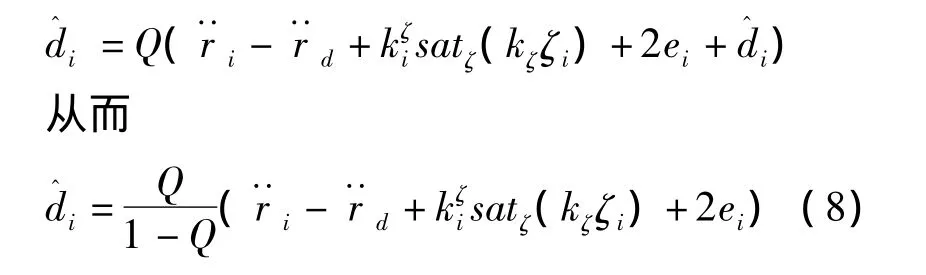
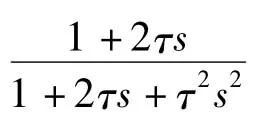
注意，虽然算法(8)中ui的选择没有速度反馈，但是此时中却引入了速度信息。为了解决这个问题，选取此 时，=很容易看出这种方法既解决了无速度反馈的问题，又满足了可实现性。

3.2 干扰误差和有界性分析

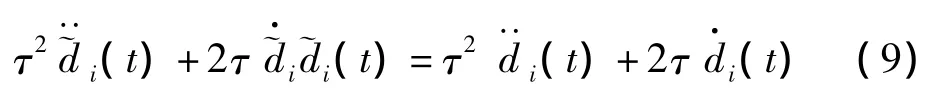
定理2:假设di具有一阶和二阶导数，且有界，即存在正实数，使得||≤和||≤， 则

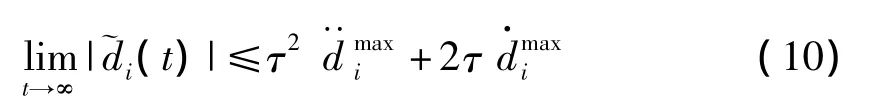
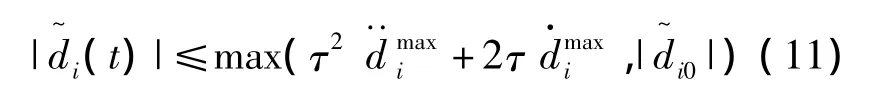
证明:解式(9)得:

因此，

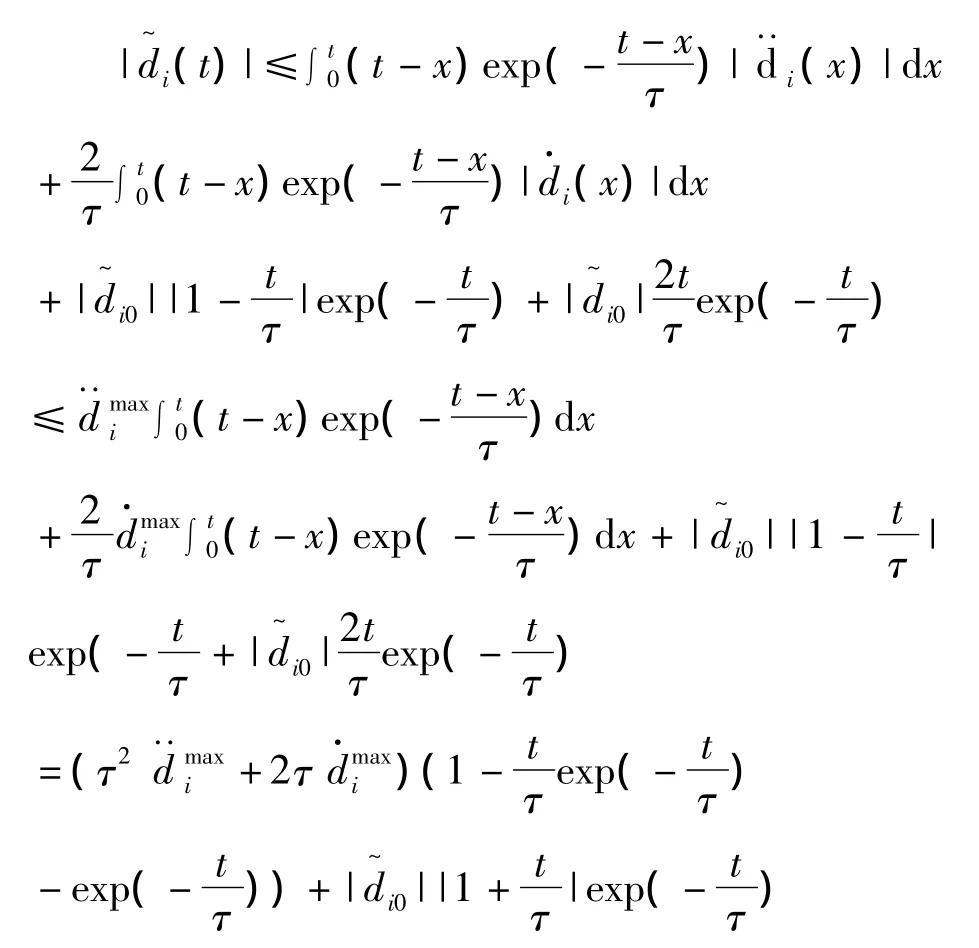
显然，当t趋于无穷时有:

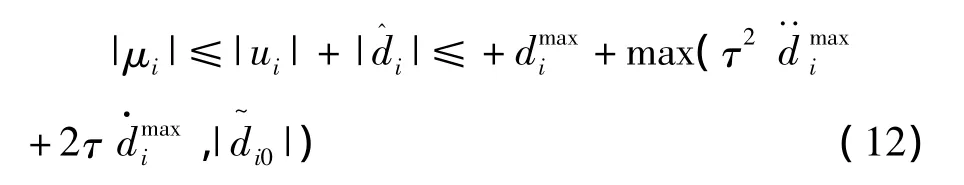
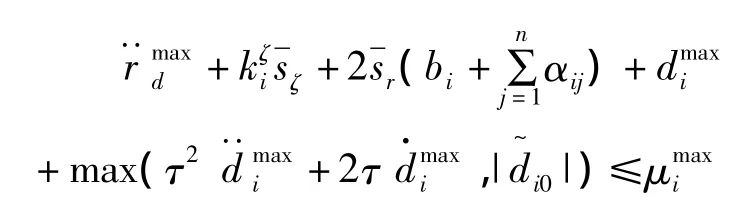
即可满足限制条件|μi|≤。

4 仿真结果

对于含有4个智能体的团队，针对模型(3)和控制算法(7)，假设它们之间的通信图如图1所示，并且权重为0.5。位置跟踪信号为rd(t)=cos(t)，对于i=1，2，3，4，ki=kζ=1，=0.5，总的干扰信号di=0.1sin(t)，时间常数 τ =0.1，从仿真结果可以看出，控制算法(7)能够很好的实现位置跟踪，如图2，并且从位置跟踪误差和干扰估计误差看(图3和图4)，算法对干扰的抑制能力得到体现，同时，控制输入是有界的，如图5。

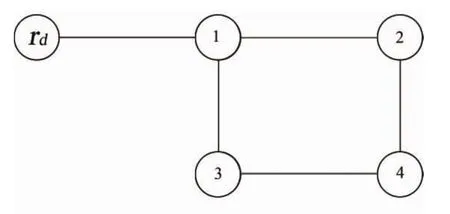
图1 通信拓扑图Fig.11 Communication topology

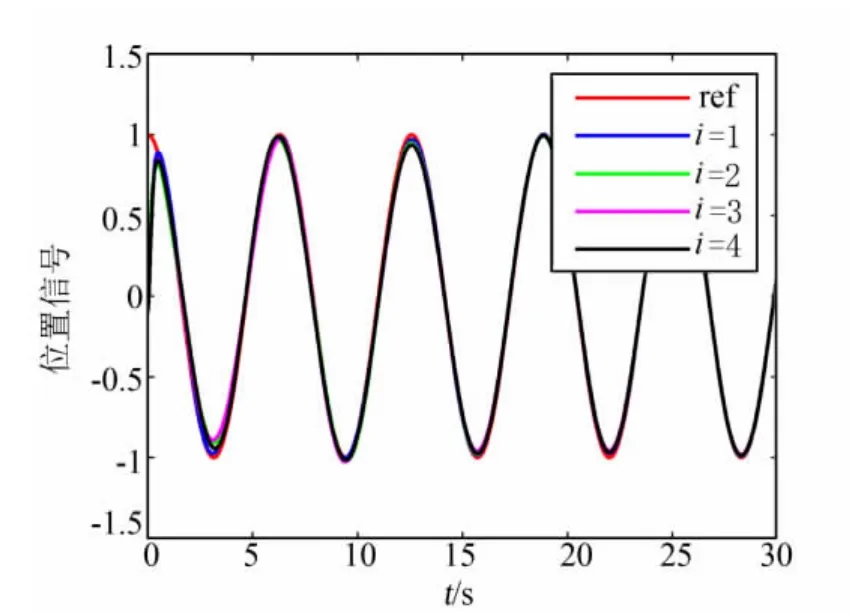
图2 位置跟踪效果Fig.2 Position tracking response

图3 位置跟踪误差Fig.3 Position tracking error response

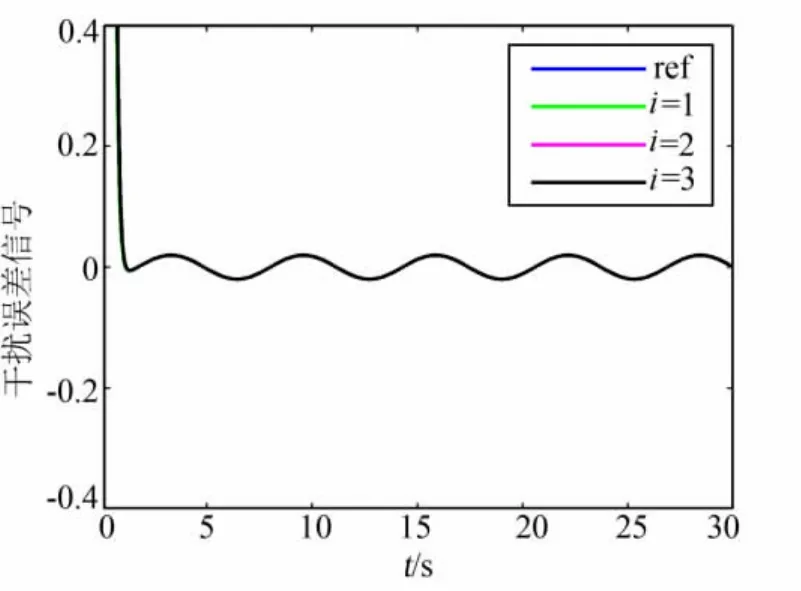
图4 干扰估计误差Fig.4 Disturbance estimate error

5 结论

图5 控制器输出Fig.5 Output of the controller

本文利用干扰估计器设计了一种位置跟踪的分布式多智能体控制算法，经过对干扰估计误差的分析，证明了算法能够出色地抑制干扰信号，同时达到无速度反馈下位置跟踪的目的。对于执行器饱和的约束，给出了控制算法有界的证明，并且具体通过控制器参数的配置来达到控制算法满足饱和约束的条件。

［1］ Jadbabaie A，Lin J，Morse AS.Coordination of groups of mobile autonomous agents using nearest neighbor rules［J］ Automatic Control，IEEE Transactions，2003，48(6):988-1001.

［2］ Hong Y，Hu J，Gao L.Tracking control for multi-agent consensus with an active leader and variable topology［J］ Automatica，2006，42(7):1177-1182.

［3］ Lin P，Jia Y，Li L.Distributed robust H∞ consensus control in directed networks of agents with time-delay［J］ Systems ＆Control Letters，2008，57(8):643-653.

［4］ 王丹晔.载人运载火箭干扰在线补偿制导方法研究［J］载人航天，2012，18(3):31-35.

［5］ Talole SE，Phadke SB.Robust input-output linearisation using uncertainty and disturbance estimation［J］ International Journal of Control，2009，82(10):1794-1803.

［6］ Kuperman A，Zhong QC.Robust control of uncertain nonlinear systems with state delays based on an uncertainty and disturbance estimator［J］ International Journal of Robust and Nonlinear Control，2011，21(1):79-92.

［7］ Deshpande VS，Phadke SB.Control of uncertain nonlinear systems using an uncertainty and disturbance estimator［J］Journal of Dynamic Systems， Measurement， and Control，2012，134(2):024501.

［8］ 刘竹生，张曙辉，容易.火箭在轨大尺寸、重负载交会对接技术研究［J］.载人航天，2012，18(2):1-6.

［9］ Zhu B，Sun W，Meng C.Position tracking of multi double-integrator dynamics by bounded distributed control without velocity measurements［C］.American ControlConference(ACC)，2013 Washington.DC，USA:IEEE，2013:4033-4038.

［10］ Ren W.On consensus algorithms for double-integrator dynamics［J］.IEEE Transactions on Automatic Control，2008，58(6):1503-1509.

［11］ Chen T，Liu X，Lu W.Pinning complex networks by a single controller［J］.Circuits and Systems I:Regular Papers，IEEE Transactions on，2007，54(6):1317-1326.