数学方法在改善逆合成孔径激光成像雷达信噪比中的应用
王晨阳,杨进华,刘智超
(长春理工大学 光电工程学院,长春 130022)
逆合成孔径激光雷达(ISAIL,Inverse Synthetic Aperture Imaging Lidar)是逆合成孔径雷达和激光雷达结合的产物。微波波段的逆合成孔径雷达,成像分辨率被信号带宽所限制,在远距离或微小目标成像时不能提供足够高的距离分辨率。为改善这个问题,将逆合成孔径技术应用于激光波段成为了一种有效的措施。激光信号有带宽大、波长短的特点,可以使ISAIL实现运动目标的超高分辨率成像。
信噪比(signal to noise ratio,SNR)是衡量雷达系统成像能力的重要指标之一。降低回波噪声功率是改善ISAIL信噪比的一种方法,它可以通过信号处理的方法实现。本文将介绍两种基于代数变换的信号降噪方法,分别为:固有值分解法(Eigen-Value Decomposition,EVD)和奇异值分解法(Singular-Value Decomposition,SVD),它们通过正交分解和投影的方法,将综合的原始信号分别投影到纯信号空间和噪声空间,在去除噪声相关子空间的同时,保持纯信号空间,进而提高ISAIL的信噪比。
1 逆合成孔径激光雷达的成像原理和信噪比
1.1 逆合成孔径激光雷达的成像原理
逆合成孔径激光雷达的成像模型如图1所示。雷达相对于运动目标固定,通过发射大带宽信号来获得很好的距离分辨率,利用目标相对于雷达转动产生的多普勒频率变化来获得好的方位向分辨率。距离-多普勒成像原理与雷达和目标运动的几何关系有关[1]。复杂运动的目标,其相对于雷达的运动形式可分解为两种简单的运动:直线运动和自身的旋转运动。将目标进行直线运动补偿后,可将运动目标简化成单纯的旋转运动。再通过相位补偿校正,可得到目标的重构成像。

图1 逆合成孔径雷达成像模型
1.2 逆合成孔径激光雷达的噪声形式
从目标返回的回波信号不可避免的要和噪声信号竞争。雷达的工作过程中噪声源有两种:一种是接收器接收到的外部噪声,另一种是雷达自身的内部噪声。内部噪声主要是系统中的热噪声,但它产生的原因不只有系统内部的热量,也有可能有外部的环境因素,如太阳光或地面、建筑物等的反射光。外部噪声会随雷达的接收方向变化而变化[2]。
由背景光子和随机信号光子引发的散粒噪声分别表示为[3]:

其中,e为电子电荷,Pb为背景光功率,γ为电流响应度,B为接收机带宽。Ps为信号功率,G为探测器增益。
探测器噪声主要包括产生—复合噪声和暗电流噪声。由载流子随机产生和复合造成的产生—复合噪声,其电流均方值可以表示为:

暗电流噪声是探测器本身的暗电流引起的闪烁噪声,探测器暗电流均方值可以表示为:

式中,ID为探测器的暗电流,Bj为接收机的带宽。放大器噪声是由放大器各电子元件带来的噪声可表示为:

式中,ηD为探测器的量子效率,H为普朗克常数,υ为激光信号的频率。热噪声是由探测器的负载电阻中的电子热运动引起的,其电流的均方值可以表示为:

式中,k为波尔兹曼常数,T为绝对温度,Rk为探测器负载电阻,Bj为接收机的工作带宽。
1.3 逆合成孔径激光雷达的信噪比
雷达信噪比SNR定义为信号峰值功率与噪声功率均方根的比值,即SNR=S/N。对于逆合成孔径激光雷达,信噪比的表达式还可以写成[4]
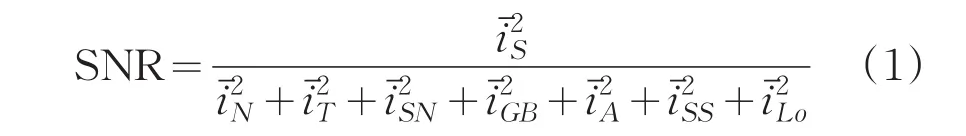
想要改善雷达的SNR,一是提高S,即提高信号的峰值功率;一是降低N,即降低噪声的功率。前者需要通过改善系统配置来实现,比如增大激光器的发射功率,但这样又面临着新的问题:发射器的功率越大,其体积和重量也要随之增加,不利于机载或星载的使用。后者可通过物理方法实现,如在系统中加入窄带滤光片等,也可使用信号处理的方法,如匹配滤波,干扰抑制等。本文提出了两种基于数学原理的降噪方法,分别为:固有值分解法和奇异值分解法。
2 两种基于数学方法的降噪过程
2.1 基于固有值分解的降噪技术[5]
基于固有值分解的降噪方法中,接收信号经由Toeplitz矩阵变换,被分解成两个子空间,分别为:噪声相关子空间和纯信号子空间。降噪的过程就是在去除噪声相关子空间的同时,保持纯信号子空间来完成的。
固有值分解,或称为Karhunen-Loève变换,使用信号相关法来降噪。N个样本带噪信号y(t)的相关矩阵为Toeplitz矩阵,由T表示:

将矩阵T进行本征向量分解

其中,λi是矩阵T的本征值,行向量P为T的本征向量。将矩阵的本征向量和本征值进行整理:使最大的本征值在矩阵的第一列,并保证本征向量和本征值一一对应。Karhunen-Loève变换的目标是用投影的方法除去噪声。通过矩阵的特征分解,在主空间内,信号y(t)可被分解成两个正交的子空间:纯信号子空间Sx和噪声子空间Sb。去噪的方法是将y(t)投影到纯信号子空间,进而得到无噪声的原始信号,如图2所示。

图2 信噪分解投影示意图
选取一个最能准确表达纯信号空间的本征向量,得到对应的本征值。求出一个新的矩阵A,该矩阵可在保持纯信号本征向量不变的情况下将噪声的本征向量化为0。这时,正交投影算子R可表示为:R=AAT。噪声信号向量y(t)通过算子R的投影产生的新向量记为Y,即:S=RTY。这里S就是最终降噪后的信号。
2.2 基于奇异值分解的降噪技术
将Hankel形矩阵看做噪声信号矩阵,构成如下的带噪信号结构:

其中,N是样本个数,L是矩阵行数,M是矩阵列数。此时,L和M的关系是:L+M=N+1,可知L>M。然后,使用奇异值分解(SVD)选择最合适的有效值:
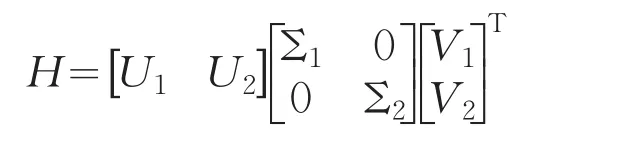
U和V分别是左、右奇异向量,Σ1表示纯信号子空间的奇异值,Σ2表示噪声子空间的奇异值。有效值在噪声信号矩阵中的对角线部分上,并且全部被提取为线性向量。根据应用的不同标准,只有一部分的有效值可以在Hankel矩阵近似法中使用。
选出合适的有效值后,构建一个新的矩阵,使对角线上的有效值矩阵变为零矩阵,从而重构一个奇异值向量,该向量包含最初获得的矩阵U和V。这样,便可以得到一个重建的信号矩阵。近似法重建的Hankel型矩阵的反对角线上的平均值给出了所有去噪信号元素。样本则由重建信号中与其相对应的矢量给出。
3 计算机仿真与降噪效果分析
采用MATLAB软件对上面介绍的两种降噪方法进行仿真。原始目标为80×80像素的二值图像,如图3所示。模拟逆合成孔径激光雷达的接收模式,对图3中的物体加转台运动[6],得到的理想回波图像(纯理想接收,无噪声),如图4所示。可以看到,理想接收情况下,目标回波是分辨率较高的点阵且目标边缘外没有任何噪声。图5为考虑系统噪声和背景随机噪声的接收回波。从图中可以明显的看出,回波的点阵的规律性被破坏,目标以外的背景空间也产生了模糊。根据前文叙述的信噪比表达式(1),求出此时回波的信噪比为SNRorigin=0.5709。

图3 原始目标图像

图4 ISAIL理想回波图像

图5 ISAIL含噪回波图像
首先采用固有值分解的方法对图5进行降噪。以原目标图形为标准建立纯信号空间的本征向量,并求出对应的本征值。将噪声投影到与纯信号空间成正交关系的信号子空间中,然后提取在纯信号空间的投影分量,得到图6的降噪结果。可以看到降噪后的分辨率比图5提高了很多,而且点阵也得到了较好的恢复。此时降噪后图像的信噪比SNREVD=0.7370。
然后,再采用与上面相似的步骤,对图5进行奇异值分解的降噪,得到结果为图7。与固有值分解法相比,奇异值法的对比度与理想回波图像更为近似,且目标周边的噪声也比图6小了很多。降噪后图像的信噪比SNRSVD=0.8445。
但值得指出的是,奇异值的分解涉及到了三个矩阵的相乘,计算量较大,对计算机系统的要求也较高。

图6 固有值分解降噪结果

图7 奇异值分解降噪结果
由上面结果可以看出,固有值分解法和奇异值分解法都有一定的降噪效果,但是它们存在一定的差异。基于固有值的分解在降噪的同时也提高了原有信号的对比度,且周边仍有较多的残余噪声。奇异值降噪法复原周边背景的效果更好,并且没有给目标信号本身带来更大的对比度,总体的降噪效果要优于固有值法的降噪。
4 结论
本文在理论分析逆合成孔径激光雷达噪声模型和信噪比的基础上,介绍了两种基于数学方法的降噪原理,对它们分别进行了MATLAB的仿真,并对比了仿真的结果,找出了两种降噪方法各自的特点:固有值分解法在降噪的同时提高了目标与背景的对比度,比较适用于目标和背景之间对比度较低的情况;奇异值分解法的降噪效果优于固有值法,且基本保持了目标信号原有的能量,但处理过程中计算量较大,比较适于目标和景物对比度明显,但对目标细节恢复要求更高的场合。
[1]费智婷.机动目标的逆合成孔径雷达成像研究[D].四川:电子科技大学,2006.
[2]Caner Ozdemir.Inverse Synthetic Aperture Radar Imaging With MATLAB Algorithms[M].Turkey:WILEY,2012:50-51.
[3]何劲,张群,杨小优,等.逆合成孔径成像激光雷达系统建模及成像仿真[J].系统仿真学报,2012,24(3):634.
[4]戴永江.激光雷达原理[M].北京:国防工业出版社,2001:14-15.
[5]CRESSEND Fabien,FAUCHARD Simon,FLOCH Julien.Algebraic methods contribution for ISAR processing[M].France:ENSEIRB-MATMECA,2009:2-4.
[6]张利军.典型目标逆合成孔径雷达成像仿真[J].甘肃科技,2009,25(8):19-20.

