一类非线性椭圆方程的Nehari流形

黄 娟，陈 丹

(1.四川师范大学数学与软件科学学院，四川成都 610066;2.成都大学信息科学与技术学院，四川成都 610106)

一类非线性椭圆方程的Nehari流形

黄 娟1，陈 丹2

(1.四川师范大学数学与软件科学学院，四川成都 610066;2.成都大学信息科学与技术学院，四川成都 610106)

研究了一类非线性椭圆方程的Nehari流形，并运用加权Sobolev空间的嵌入定理和齐次特征值问题的性质，分析了Nehari流形与fibrering映射的关系，进而讨论了Nehari流形的性质，运用这些性质还可得到该非线性椭圆方程正解的情况.

Nehari流形;变分方法;加权Sobolev空间

0 引言

本研究考虑一类非线性椭圆方程，

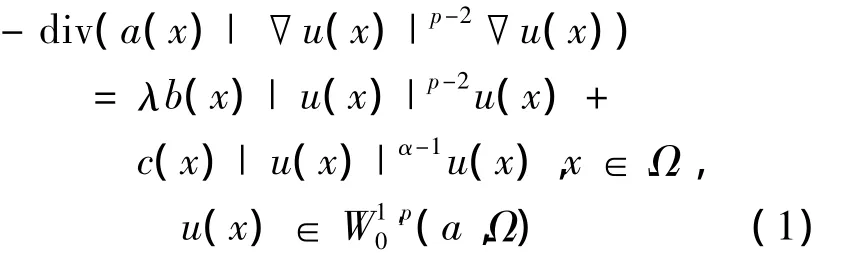
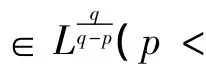
(a，Ω)是以a(x)为权函数的加权Sobolev空间，其范数是.权函数a(x)满足，

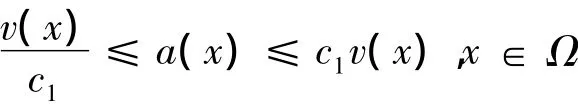
其中，c1≥1，v也是一个权函数且满足，

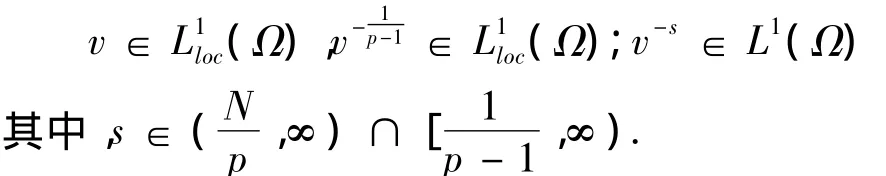
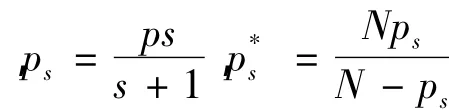
对于方程(1)，当 a(x)≡ 1，p=2时，Amann等［1］运用全局分歧理论研究了方程在二阶Laplacian算子为自共轭算子时的正解的存在性和重度问题;当a(x)≡1 时，Binding［2，3］等运用变分方法研究了方程的正解和多解的存在性问题.在此基础上，本研究将运用文献［4］中的方法，得到方程(1)的Nehari流形的性质，进而讨论了方程(1)正解和多解的存在性问题.

令λ1(b)是方程，

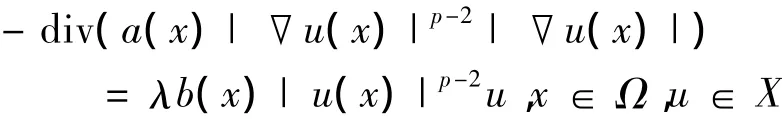
的第一特征值，且其对应的特征函数为≪1［6］.进而，本研究的主要结论为:

定理1

①当0＜λ＜λ1(b)时，方程(1)存在一个正解;

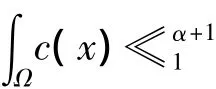
1 Nehari流形的性质

考虑方程(1)的Euler函数，

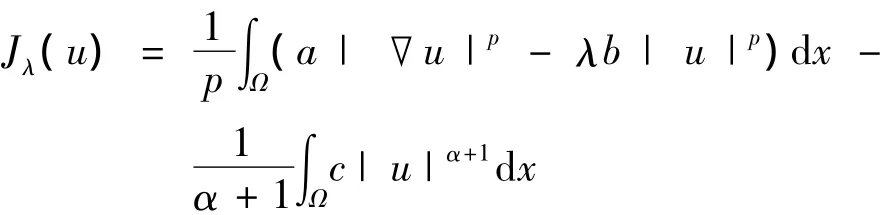
为了得到存在性结论，引入Nehari流形，

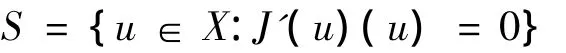
因此，u∈S当且仅当∫Ω(a|▽u|p-λb|u|p)dx-∫Ωc|u|α-1dx=0.显然，Jλ的临界点在S上，并且S上的局部极值即是Jλ的临界点.此外，为了方便起

见，用∫·dx表示∫Ω·dx.

在S上考虑Jλ，则有，

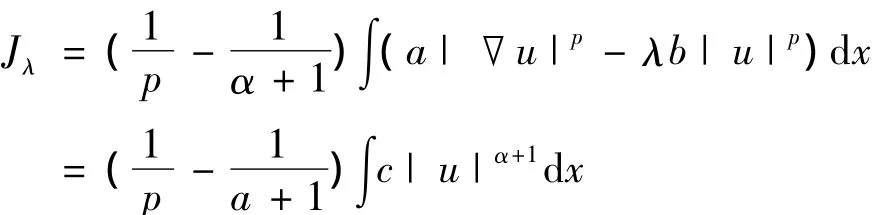
对于Nehari流形，它与映射≪u:t→Jλ(tu)(t＞0)有密切的关系，如果u∈X，则，

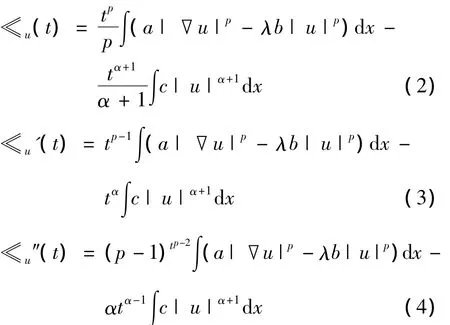
显然，u∈S当且仅当≪u'(1)=0.更为一般的，如果≪u'(t)=0当且仅当tu∈S.也就是说，S中的元素是fibrering映射的不动点.又由式(3)和(4)可知，如果≪u'(t)=0，则≪u″=［(p-1)-α］∫c|u|α-1dx.那么，很自然地可以把S分成以下3部分，

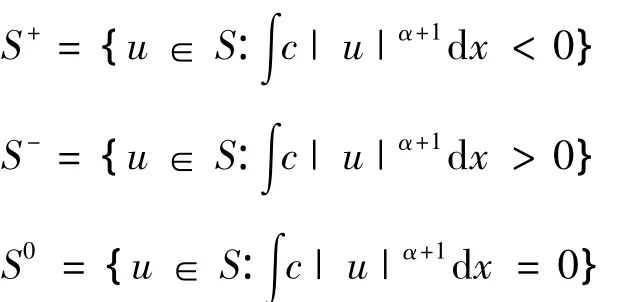
分别对应于fibrering映射的局部极小值、局部极大值和拐点.从而，若u∈S，则，≪u'(1)=0;如果≪u″(1)＞0，≪u″(1)＜0，≪u″(1)=0，分别有u∈S+，S-，S0.令，u∈X，

① 若∫(a|▽u|p-λb|u|p)dx与∫c|u|α+1dx同号，≪u有惟一拐点，且在拐点处，

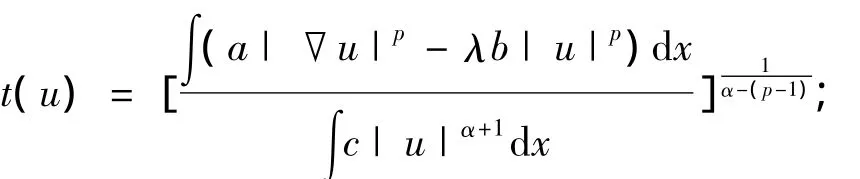
② 若∫(a|▽u|p)dx与∫c|u|α+1)dx异号，≪u没有拐点，也因此S中无u的任意倍式.

定义，

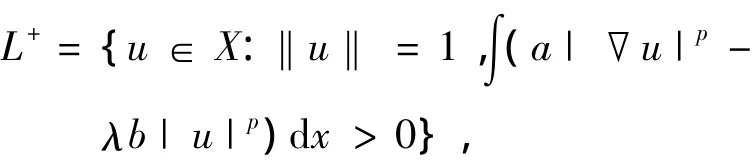
同样地，分别用“＜”和“=”代替“＞”，可以定义，L-1和L0.

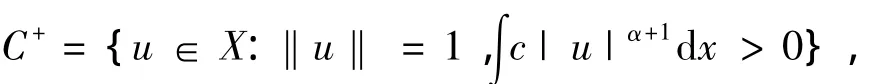
类似的，也可以定义C-和C0.

从上面的分析可知:

① 如果u∈L+∩C+，则t→≪u(t)在t=t(u)时达到其局部极大值，且t(u)u∈S-;

② 如果u∈L-∩C-，则t→≪u(t)在t=t(u)时达到其局部极小值，且t(u)u∈S+;

③ 如果u∈L+∩C-(或L-∩C+)，则t→≪u(t)是严格单调增加的(或减少的)，且在S中无u的倍式.

引理1［6］当1≤r＜p*时，XLr(Ω)是紧嵌

s入.进而，XLp(Ω)是紧嵌入.

定理2 若0＜λ＜λ1(a)，则S=S-∪{0}，且S-={t(u)u:u∈C+}.

证明 由于问题，-div(a(x)|▽u(x)|p-2▽u(x))-λb(x)|u(x)|p-1=μu(x)p-1，x∈Ω，u(x)=0，x∈ ∂Ω的特征值μ(λ)＞0［5］.因此，∫(a|▽u|p-λb|u|p)dx＞μ(λ)∫|up|dx，对于u∈X{0}.用反证法容易得到，存在δ＞0使得，

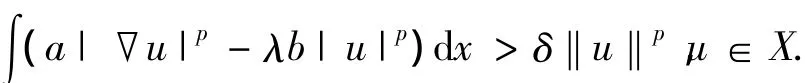
因此，L-=L0=≪，进而S+=≪，S0={0}.所以，S=S-∪{0}并且S-={t(u)u:u∈C+}.

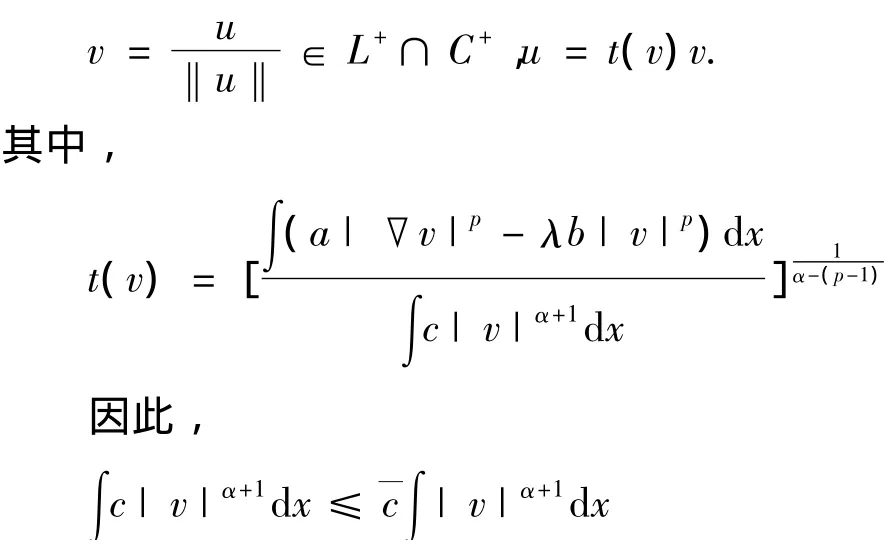
证明 设u∈S-，则，

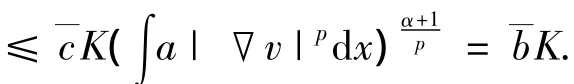
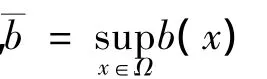
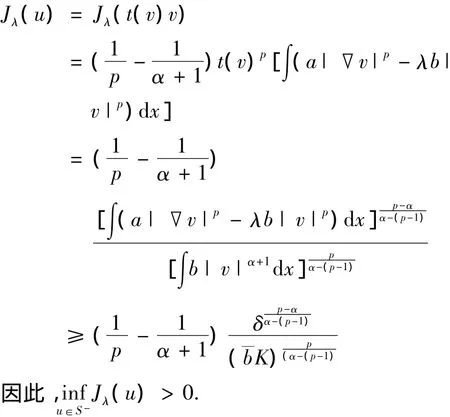
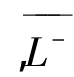
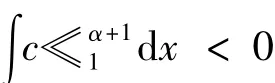
证明 设其不成立，则存在序列{λn}和{un}满足‖un‖=1，λn→(b)以及，

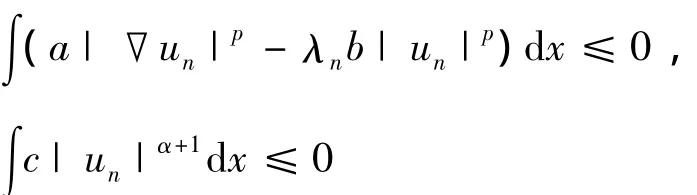
因为{un}有界，因而可设un⇀u0于X，un→u0于Lp(Ω)和Lα+1(Ω).

下面将证明un→u0于X假设不成立，则有，

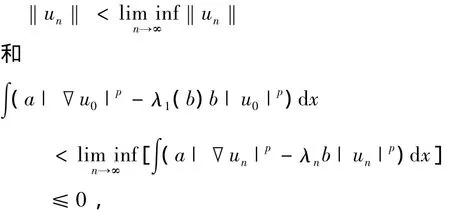
矛盾.因此，un→u0，‖u0‖=1.由此得，

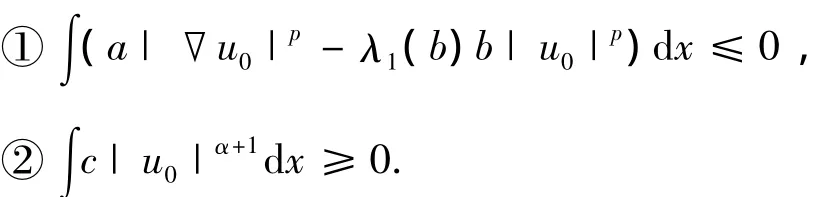
但是，由①可知存在某个k使得u0=k≪1，而由②可得k=0.这与‖u0‖=1矛盾.因此，结论获证.

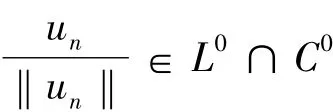
②假设结论不成立，则存在{un}∈S-使得un→0于X.因此，

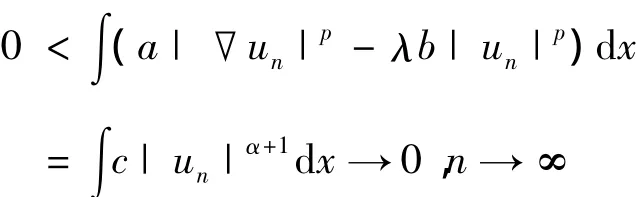
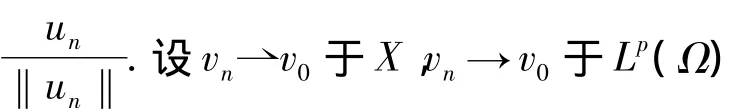
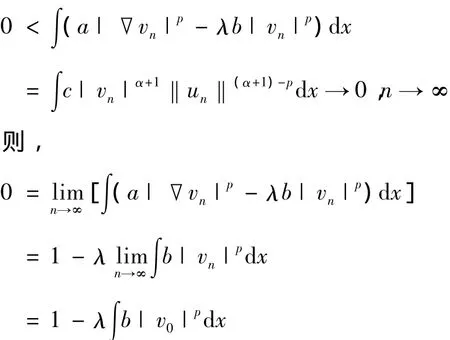
所以，v0≠0.而且，

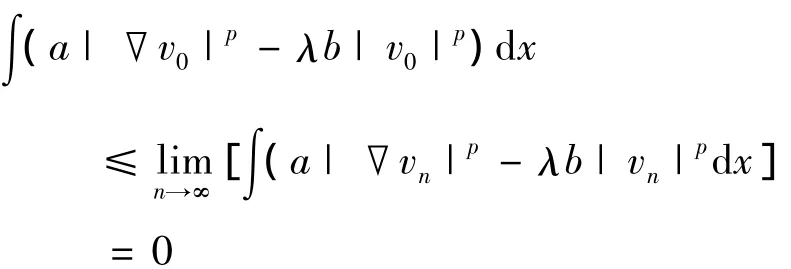
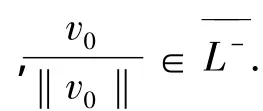
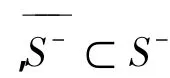
③由①和②有，

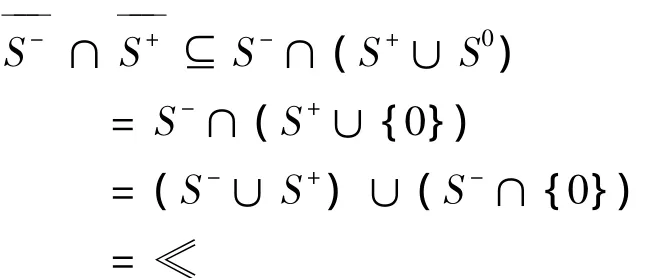
则，S-和S+是分离的.

④设S+无界，则存在{un}∈S+使得，

—

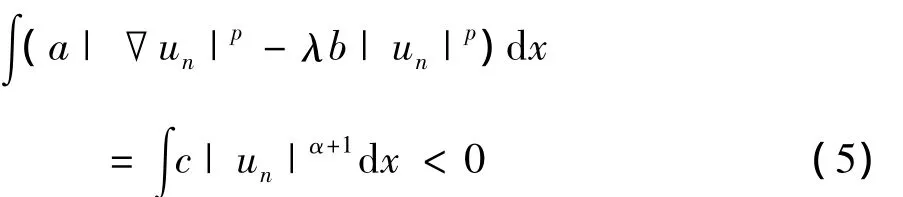
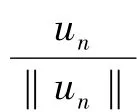
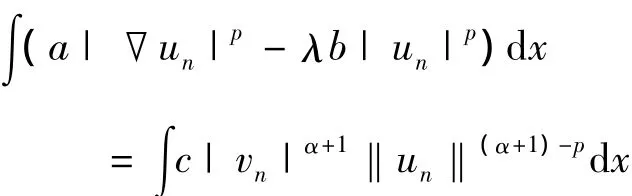
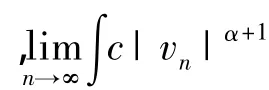
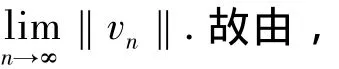
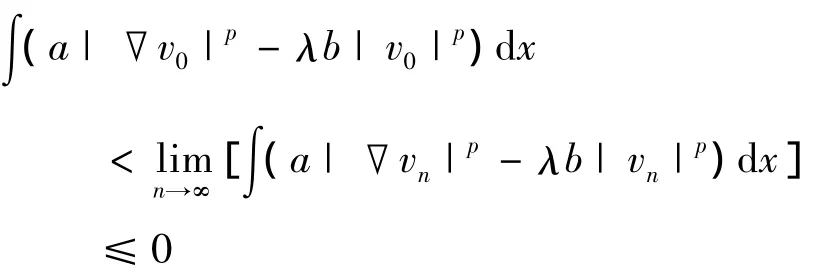
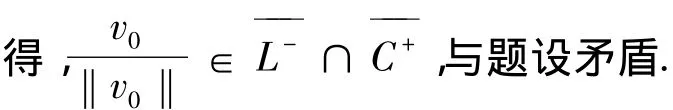
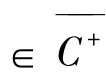
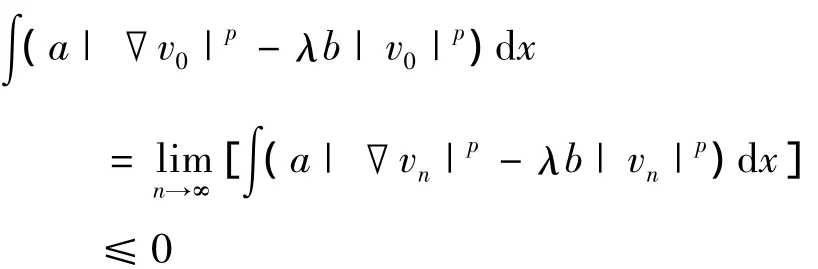
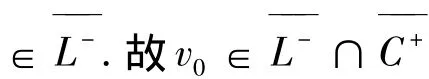
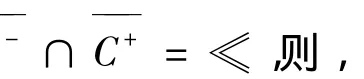
①Jλ(u)在S-上的每一个极小化序列有界;

证明 ①设{un}∈S-是一列极小化序列.则，

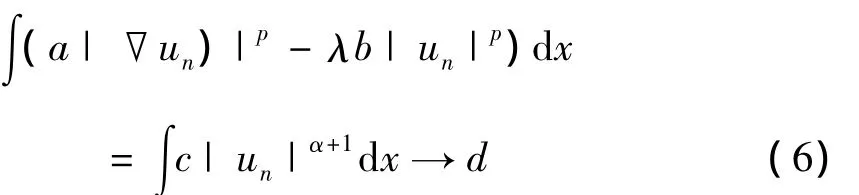
其中，d≥0.

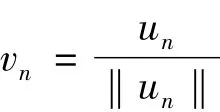
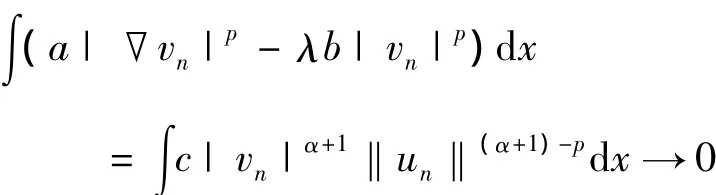
由‖un‖→+∞，得，

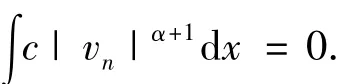
下面证明vn→v0于X.假设其不成立，则，

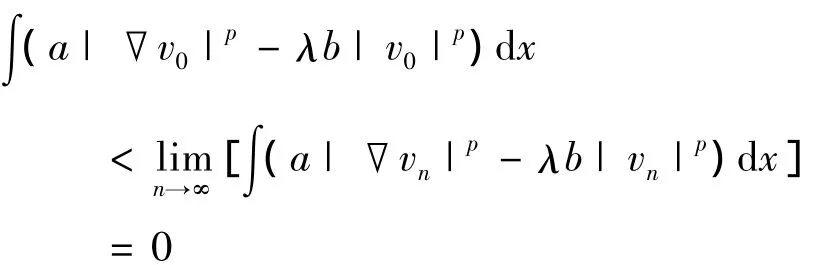
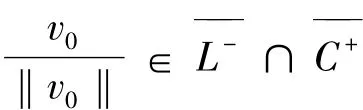
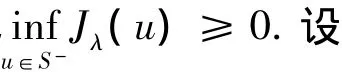
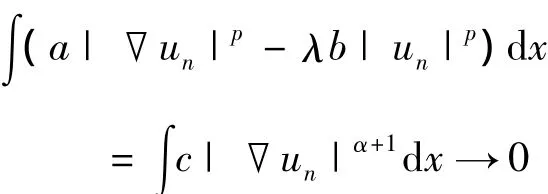
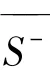
2 解的存在性

定理7 若u0∈S-是S-上的极小值，则u0既是Jλ(u)的临界点，也是式(1)的非平凡解.

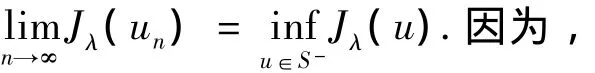
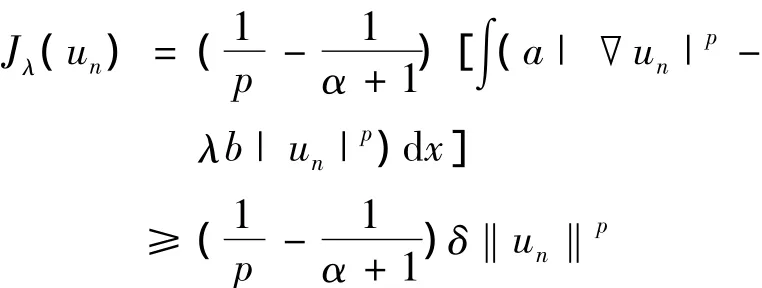
且{un}在X有界，则存在{un}的子序列(为了方便起见仍记为{un})，由定理2有，un⇀u0于X，un→u0于Lα+1(Ω)和Lp(Ω).

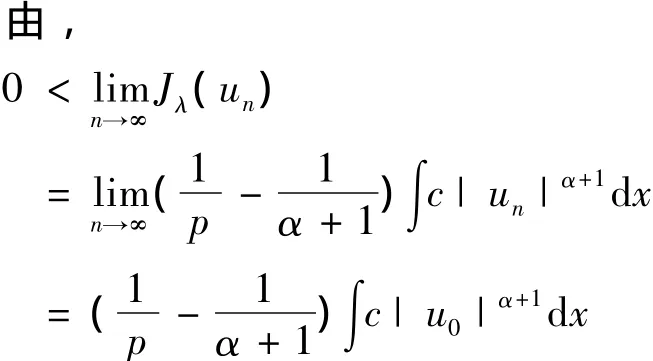
有u0≠0.因为λ＜λ1(b)，∫(a|▽u0|p-λb|u0|p)dx＞0，即，u0∈L+.故u0∈L+∩C+.

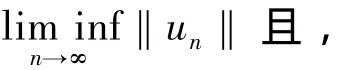
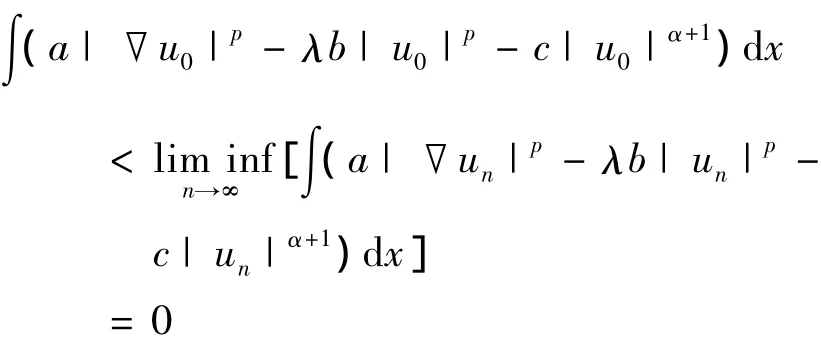
另一方面，

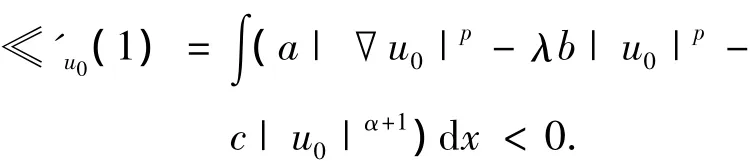
这与Nehari流形的性质分析矛盾.由此可知，存在β＜1，使得≪u0(β)=0，即，βu0∈S-.则βun⇀βu0于X.又由un∈S-映射≪un在t=1处达到其极大值，因此，

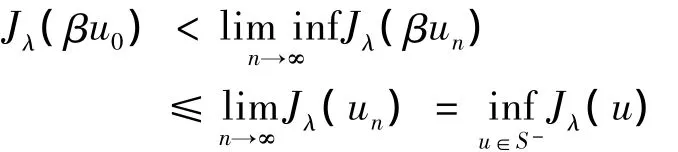
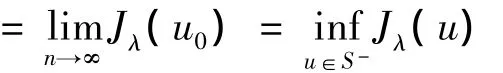
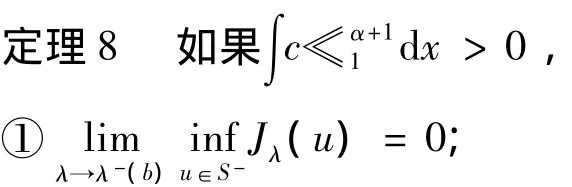
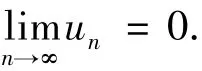
证明 ①不失一般性，设‖≪1‖=1.因为∫c≪α+1dx＞0，≪1∈C+.又由于λ＜λ1(b)，≪1∈L+，则≪1∈L+∩C+.因此，t(≪1)≪1∈S-.其中，

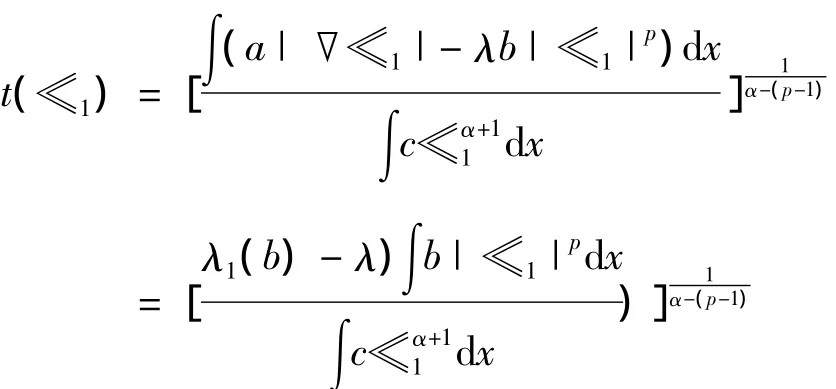
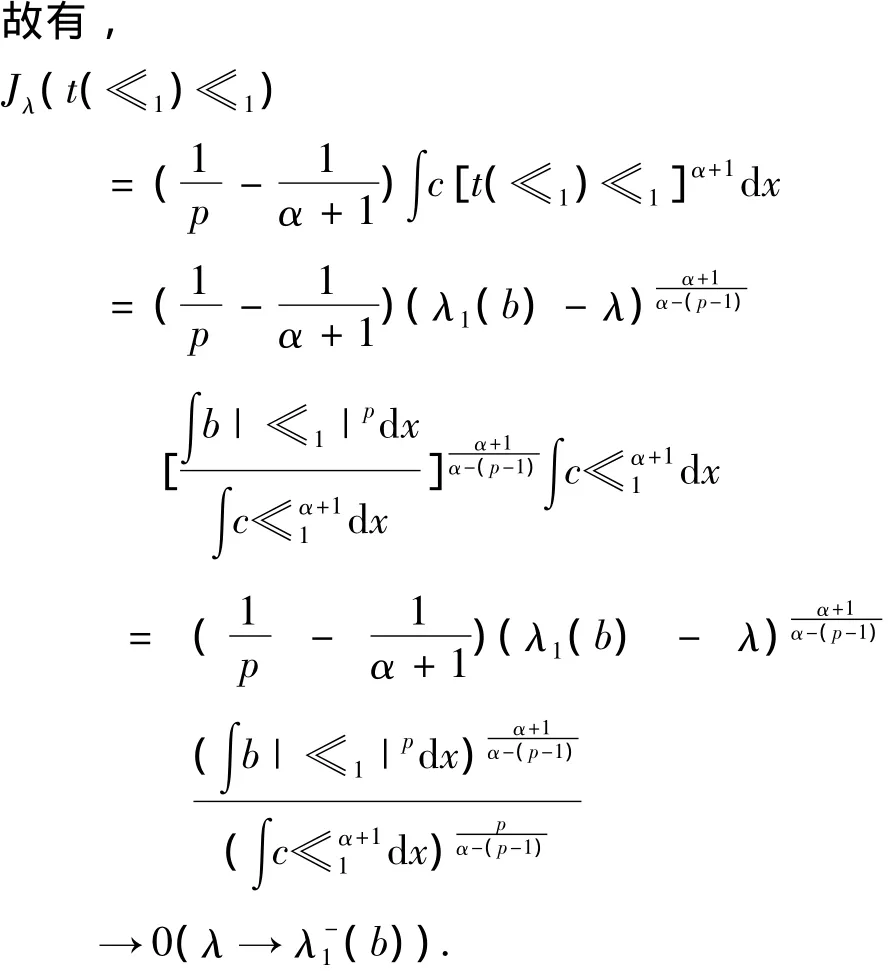
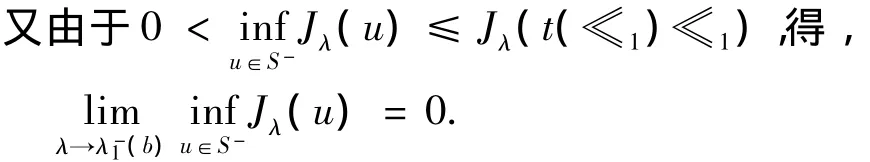
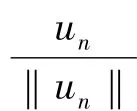
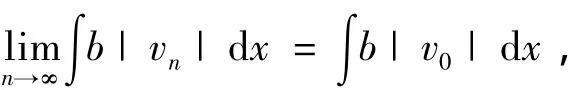
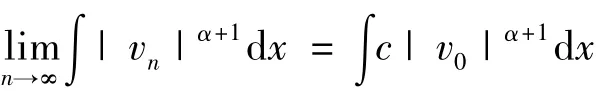
又由于当n→∞时，

矛盾.所以，vn→v0.

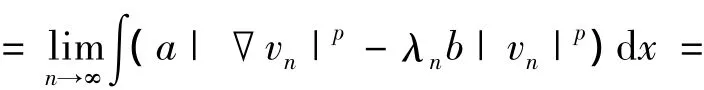
不失一般性假设u0→u0于X.运用上面对于{vn}的讨论基本相同的方法讨论{un}可以得到un→u0及u0=0.从而结论获证.

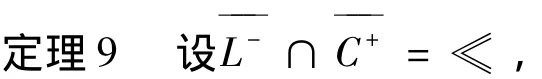
①则在S-上存在Jλ(u)的一个极小值;

②若L-≠≪，则在S+上存在Jλ(u)的一个极小值.

证明 ①令{un}是一个极小化序列.则，

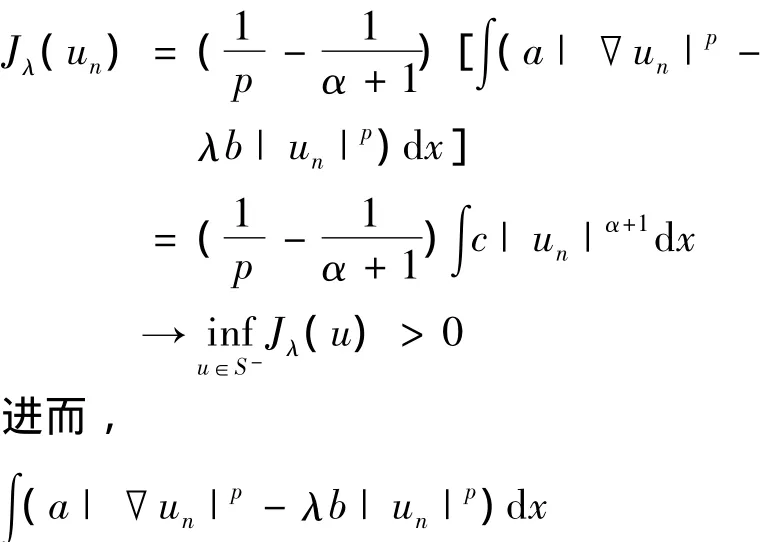
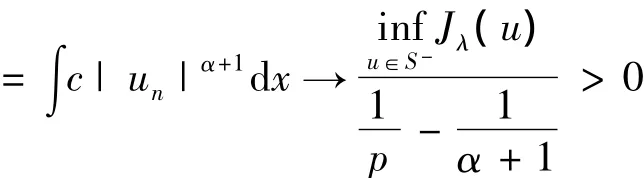
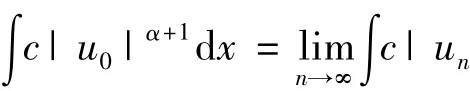
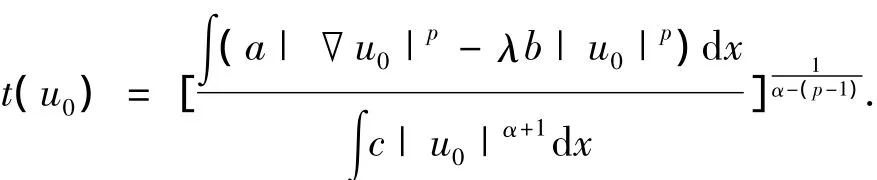
下面证明，un→u0.假设不成立，则，

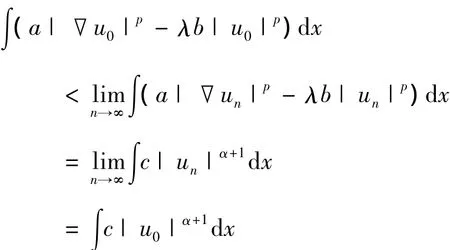
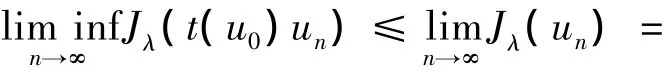
由此易得，

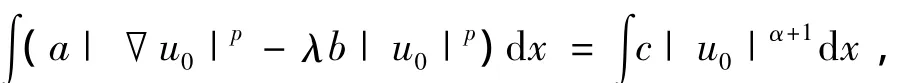
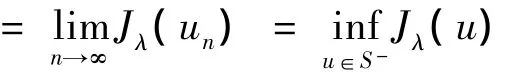
Jλ(u)在S-上的极小值.

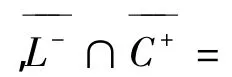
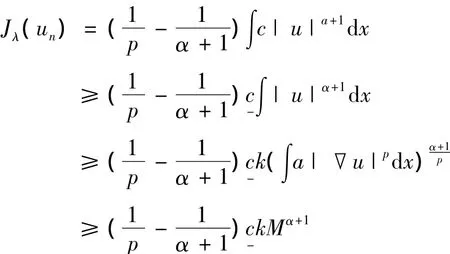
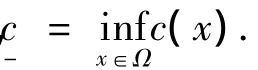
设{un}是S+上的极小化序列，则当n→∞ 时，

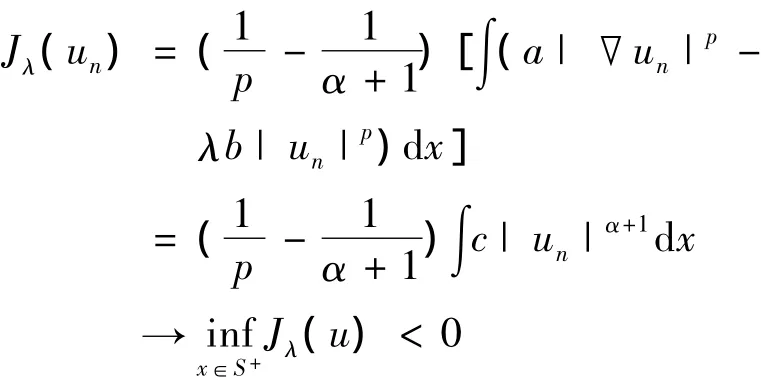
由于S+有界，可设u0⇀u0于X，un→u0于Lp(Ω)和Lα+1(Ω).则，

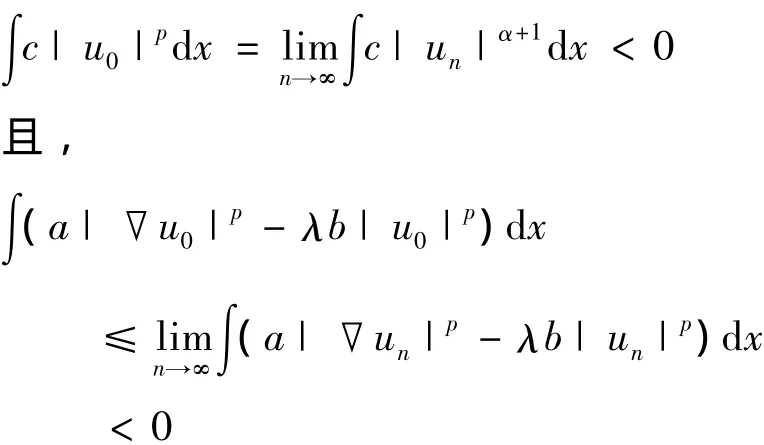
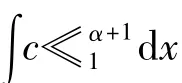
证明 当λ＞λ1(b)时，≪1∈L-时，则L-≠≪.因此，由定理9知，存在δ＞0使得当λ1(b)＜λ＜λ1(b)+δ时Jλ分别在S-和S+上存在极小值.因为Jλ(u)=Jλ(|u|)，所以可设这些极小值为正.由定理5知S-和S+是分离的，且S0={0}.则这些极小值是S上的局部极小值且不在S0中，因而其是方程(1)的正解.

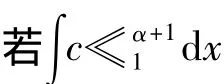
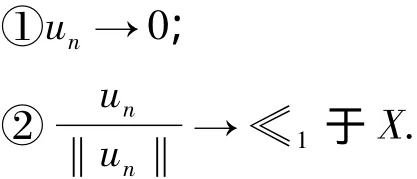
证明 ①由于S+有界，因此可设un⇀u0于X，un→u0于Lp(Ω)和Lα+1(Ω).同样，∫(a|▽un|pλ1b|un|p)dx=∫c|un|α+1dx＜0，∀n.

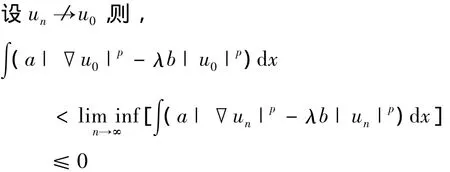
矛盾.因此，un→u0.由此可得，

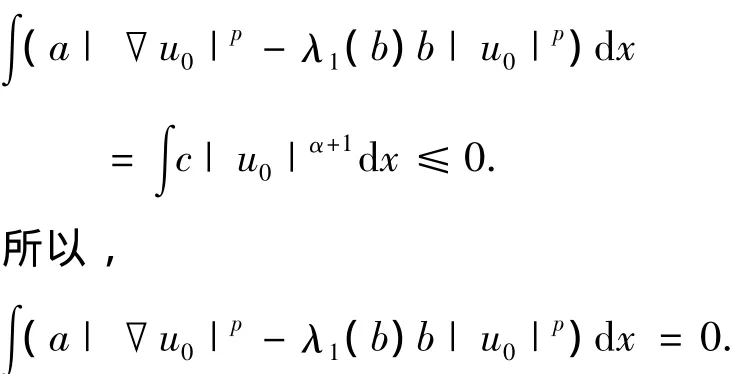
故对于某个k有u0=k≪1，但是，由于＜0，所以k=0，即un→0.

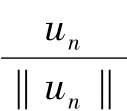
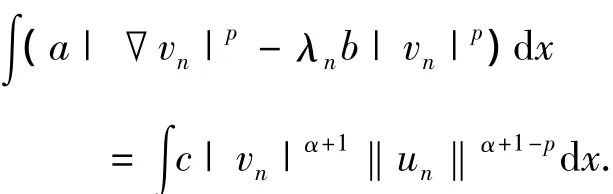
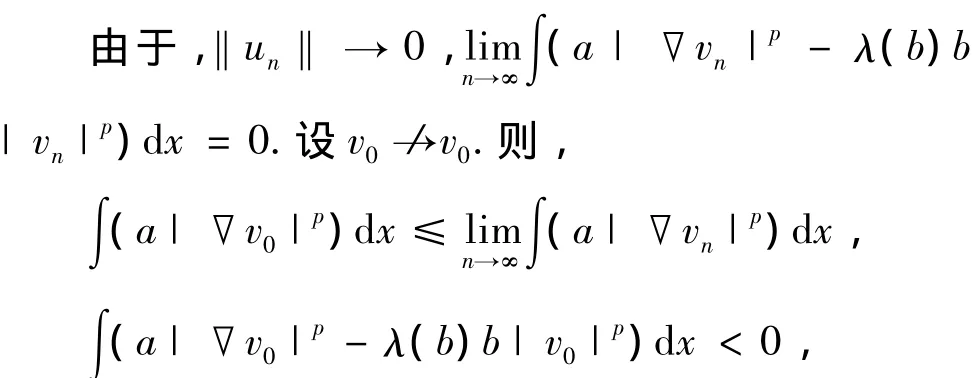
矛盾.因此，vn→v0.由此可得，‖v0‖=1，∫(a|▽v0|p-λ1(b)b|v0|p)dx=0.所以，v0=≪1，结论获证.

3 无解的情况

引理2 设L-∩C+≠≪，则存在δ＞0使得当λ1(b)≤λ＜λ1(b)+δ时有L-⊂C+.

由这个引理可以知道，如果该引理的条件成立，则L-∩C-≠≪且S+=≪.另一方面，S-≠≪.讨论S-，有以下结论，

定理11 若L-∩C+≠≪，则inf

u∈S-Jλ(u)=0.

证明 令u∈L-∩C+，可以取到h∈X使得它有足够小的上确界范数但有足够大的X范数，使得，

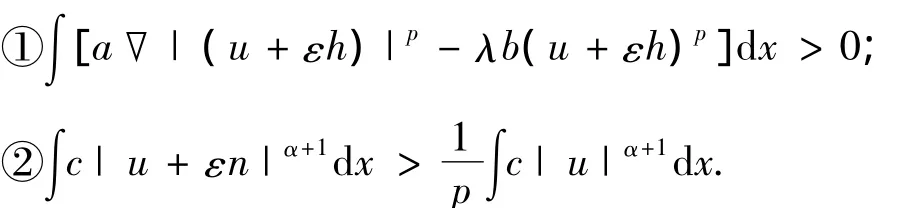
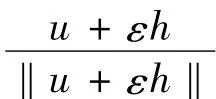
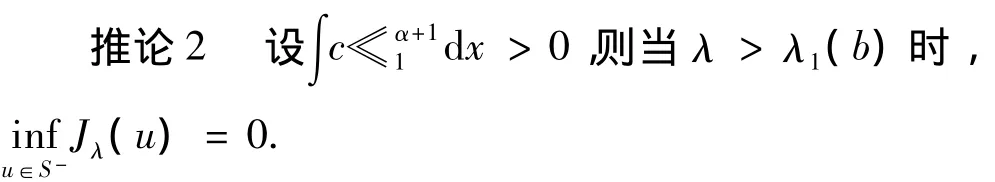
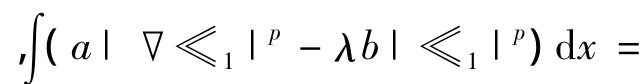
因此，Jλ在S+上无下界.

推论4 存在λ*＞0，当λ＞λ*时Jλ在S+上有下界.

证明 取u∈X使得‖u‖=1，∫c|u|α+1dx=0和∫b|u|pdx＜0.则当λ足够大时u∈L-∩C0，从而结论获证.

:

［1］Amann H，López-Gómez J.A priori bounds and multiple solutions for superlinear indefiniteelliptic problems［J］.Journal of Differential Equations，1998，146(2):336-374.

［2］Binding P A，Drabek P，Huang Y X.On Neumann boundary value problems for some quasi-linear elliptic equations［J］.Electionic Journal of Differential Equations，1997，197(5):1-11.

［3］Binding P A，Drabek P，Huang Y X.Existence of multiple solutions of critical quasilinearelliptic Neumann problems［J］.Nonlinear Analysis，2000，42(4):613-629.

［4］Brown K J，Zhang Y P.The nehari manifold for a semilinear elliptic equation with a sign-changing weight function［J］.Journal of Differential Equations，2003，193(2):481-499.

［5］Hess P，Kato T.On some linear and nonlinear eigenvalueproblems with an indefinite weightfunction［J］.Communications in Partial Differential Equations，1980，5(10):999-1030.

［6］Drábek P，Kufner A，Nicolosi F.Quasilinear elliptic equations with degenerations and sin-gularities［M］.New York:Walter de Gruyter Berlin，1997.

［7］Ma L.Bifurcation in nirenberg’s problem［J］.Comptes Rendus de I ＇Académie des Sciences-Series I-Matyhematics，1998，326(5):583-588.

［9］Bao J G.Positive solution for semilinear elliptic equation on general domain［J］.Nonlinear Analysis，2003，53(7):1179-1191.

［10］Shen Y T，Yan S S.Eigenvalue problem for quasilinear elliptic systems with limiting non-linearity［J］.Acta Mathematica Sinica，1992，8(2):135-147.

Nehari Manifold of Nonlinear Elliptic Equation

HUANG Juan1，CHEN Dan2

(1.College of Mathematics and Software Science，Sichuan Normal University，Chengdu 610066，China;2.School of Information Science and Technology，Chengdu University，Chengdu 610106，China)

In this paper，we study the Nehari manifold of a nonlinear elliptic equation.By investigating the compact imbedding theorem and the properties of homogeneous eigenvalue problem in weighted Sobolev space and exploiting the relationship between the Nehari manifold and fibrering maps，we discuss the properties of the Nehari manifold.Using these properties，we also derive out the existence and non-existence results for positive solutions of the equations.

Nehari manifold;variational methods;weighted Sobolev space

O175.25

A

1004-5422(2013)04-0343-09

2013-06-25.

四川省教育厅青年科研基金(10ZB003)资助项目.

黄 娟(1981—)，女，博士，讲师，从事偏微分方程研究.