孔隙热弹性梁的非线性气弹性特性*

朱媛媛 李莹 程昌钧

(1．上海师范大学计算机科学与技术系，上海 2 00234)(2．上海大学力学系，上海 2 00444)

孔隙热弹性梁的非线性气弹性特性*

朱媛媛1†李莹2程昌钧2

(1．上海师范大学计算机科学与技术系，上海 2 00234)(2．上海大学力学系，上海 2 00444)

根据作者由Hamilton变分原理导出的一个孔隙热弹性梁的非线性数学模型和气弹性原理中的一阶修正线性活塞理论，本文首先给出了位于高速或者超高速流动中两端固定的平面孔隙热弹性梁的控制微分方程和定解条件，其中基本未知量是梁的轴向和横向位移以及孔隙百分比和温度变化引起的“力矩”．为了考察孔隙热弹性梁在横向载荷和气弹性载荷联合作用下的非线性力学特性，采用微分求积方法对问题进行空间离散，得到一组关于时间的非线性常微分方程，然后在给定初始条件下采用变步长Runge－Kutta方法对方程组进行数值求解，由此研究了孔隙热弹性梁的气弹性特性，考察了参数的影响，得到了一些有益的结论．

孔隙热弹性梁， 有限变形， 线性活塞理论， 微分求积方法， 气弹性特性

引言

孔隙热弹性材料兼具结构和功能双重用途，多见于天然多孔材料、人造多孔材料和生物工程材料等．这种材料具有相对密度低、比强度高、比表面积高、重量轻、隔音、隔热、渗透性好等优点，在航空、航天、化工、建材、冶金、原子能、石化、机械、医药和环保等领域具有广泛的应用前景．同时，新型孔隙材料正逐渐地被用作绝缘、缓冲、吸收冲击能量的材料，从而发挥了其由多孔结构决定的独特的综合性能．因此，对孔隙热弹性材料理论的研究引起了很多学者的兴趣．主要研究内容包括两个方面，其一是孔隙热弹性材料性质的合理描述与本构关系的表达，其二是孔隙热弹性材料和结构的相关问题的求解．经过Goodman，Cowin和Iesan等众多学者的发展，已经形成了一个较为统一的孔隙热弹性理论［1－4］．

作为最基础的结构元件，梁在建筑结构、桥梁结构、水工结构、地下结构、飞机结构、船舶结构、海洋工程结构、空间工程以及微机电系统等许多领域具有广泛应用．文献［5］在有限变形的条件下，把Hamilton变分原理推广到孔隙热弹性梁中，由此给出了孔隙热弹性梁的一个以中性轴的3个位移、孔隙百分比和温度引起的“力矩”所表示的非线性数学模型，并考虑了轴力、中性层惯性和转动惯性的影响．本文以此模型为基础，研究了两端固定的孔隙热弹性平面梁在气动力作用下的非线性力学行为，其中气动力采用修正的一阶线性活塞理论来模拟．由于问题的非线性性，难以得到其解析解或者半解析解，因此采用微分求积方法(Differential Quadrature Method，简称DQM)对数学模型进行空间离散，再采用Runge－Kutta方法对离散化的动力系统进行数值求解，在此基础上研究了孔隙热弹性梁的气弹性特性，得到了一些有益的结论．

1 问题的数学描述

由Iesan［4］提出的孔隙热弹性材料的动力学理论，有如下孔隙的运动微分方程、熵均衡方程和各向同性孔隙热弹性梁的本构方程

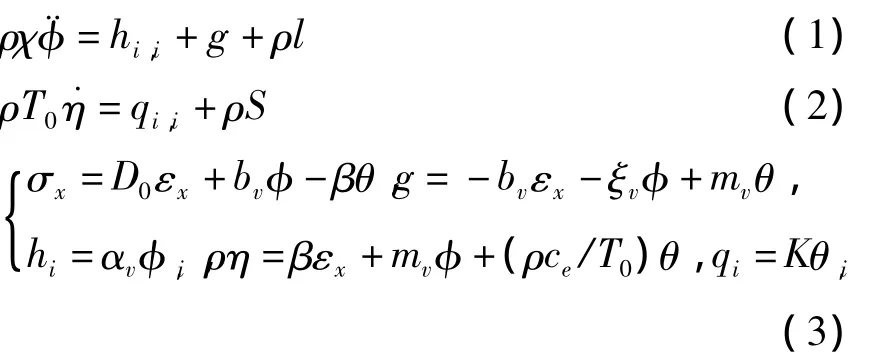
这里，ρ为参考构形的密度，φ为基体材料体积百分比的变化，χ和hi是平衡惯量和平衡应力向量，g和ρl是内外平衡体积力，η和S分别是单位质量的熵和热源，qi是热流矢量，σx为梁的应力分量，θ=T－T0表示温度的变化，其中T是物体的绝对温度，T0是参考构形的绝对温度．D0=E(1－v)/［(1+v)(1－2v)］，β=αtE/(1－2v)，E，v分别是弹性模量和泊松比，αt是线性热膨胀系数，K是热传导系数，ce是比热，同时 αv，bv，ξv，mv是与孔隙有关的材料参数，它们的物理意义可在文献［4］中找到．

现在考察图1所示长度为l，宽度为b，厚度为h的孔隙热弹性平面梁．取坐标原点o与梁一端的截面的惯性主轴的交点重合，ox－轴为梁的中性轴，oy－轴和oz－轴为截面的惯性主轴，并组成右手坐标系．设中性层的位移分别为u，v，w，基于 Kirchhoff－Love假设，当挠度w与宽度b和厚度h同阶，并且梁的长度远大于宽度和厚度时，有非线性几何关系

其中，εx为应变分量，εx0为中性轴的应变分量．

图1 梁的模型Fig．1 The model of the beam

其中，ρh¨u和ρIy¨w，xx分别是中性层的惯性项和转动惯性项，p是横向的分布保守力，N0是端部轴力．另外，根据文献［5］，qφ和qθ是两个分别与Mφ和Mθ有关的量，被给定为

边界条件:对于x=0，l两端固定的不受轴力N0作用的孔隙热弹性梁，有如下边界条件:

初始条件:假设初始时刻t=0时，有初始条件

其中，u0，w0，，，都是x的已知函数，特别当初始时刻梁处于静止时，这些函数为零．

2 孔隙热弹性梁非线性气弹性分析的控制微分方程

处于高速和超高速气流中的弹性结构往往会发生颤振，即所谓的气动弹性问题，这种现象是由于空气动力及其引起的弹性结构反作用力之间的相互影响而产生的．飞行器以及处于自由风速流动中的高层结构容易会发生这种问题．气动弹性力学大致可分成两大分支:一是飞行器气动弹性力学，主要研究飞机、直升机、导弹、火箭直至航天飞机和卫星等飞行器的气动弹性问题，这方面的知识已成为设计和制造先进的飞行器所必备的基础;另一是建筑结构气动弹性力学，主要研究大型高层建筑、桥梁、高空电缆、龙门吊车以及细长的船舶桅杆、电视尖塔、烟囱等各种具有弹性性质的建筑物的气动弹性问题，是近年来蓬勃发展的一个学科分支．由于这些建筑结构几乎与国民经济的所有部门有关，因此保证它们的安全和工作可靠具有极其重要的意义［6－7］．

气动力计算是气动弹性分析的重要组成部分，活塞理论由于形式简单，且具有较好的精度，被广泛应用于计算分析中，本文中采用修正的一阶线性活塞理论来模拟气动压载荷［7］

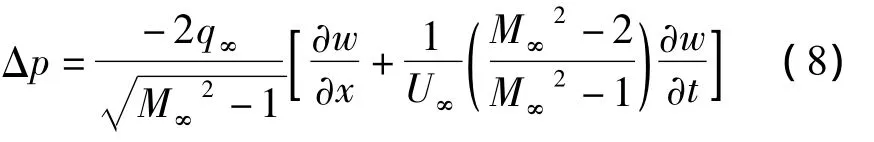
引入如下的无量纲变量和参数:

将(9)代入方程(5)～(8)中，则有如下无量纲的控制微分方程和定解条件:

其中，θ+，θ－是上下表面的温度．Δp为气动力的无量纲化，即

边界条件无量纲化为

假设初始时刻静止，则有无量纲初始条件为

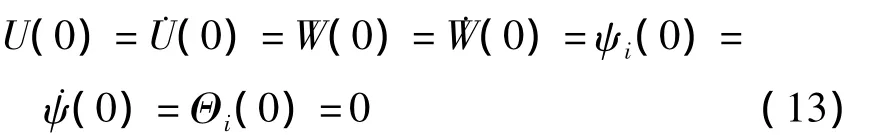
3 求解方法与数值解的验证

现在，采用微分求积方法(Differential Quadrature Method简称DQM)对控制方程(10)～(11)和定解条件(12)～(13)进行空间离散．DQM是由Bellman等人［8－9］于 1971 ～1972 年提出的一种数值求解方法，现已广泛应用于各个领域［10－12］．其基本概念是将函数对某方向的自变量的偏导数近似表达为沿该自变量方向各离散点(节点)处相应函数值的加权和，其加权系数取决于试函数和节点分布，而与具体问题无关．因此，利用这些系数，任何偏微分方程都能转化为相应的常微分方程或者代数方程，然后再求解．根据 DQM的概念和公式［10－11］，可得无量纲控制微分方程(10)的 DQ 离散化形式为:其中，Δpi为无量纲气动力(11)的DQ离散化，被给定为

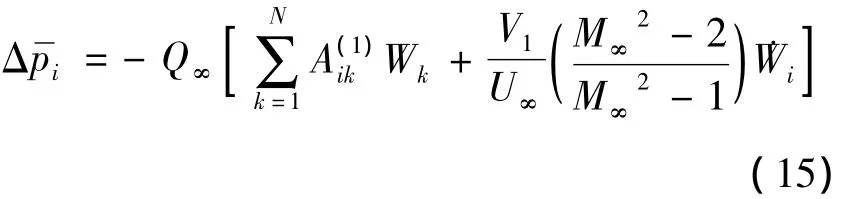
在(14)～(15)式中，i=1，2，…，N，N为所布置的结点数表示对x的j阶偏导数的权系数，并且上面具有圆点的量表示对时间τ的导数．本文采用多项式作为试函数来构造权系数，并利用Chebyshev－Lobatto多项式的零点的坐标来布置节点［10－11］．

边界条件(12)的DQ离散化形式为

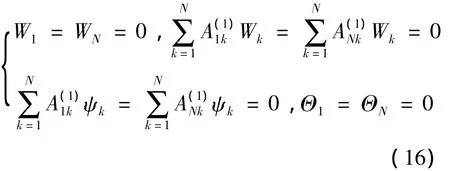
同时，初始条件(13)的DQ离散化

这样，对于孔隙热弹性平面梁的气动力学问题，就是在给定边界条件(16)和初始条件(17)条件下，求解非线性常微分方程组(14～(15)．

图2 DQ数值解与解析解的对比(a)=10－5;(b)=10－4Fig．2 Comparison between the numerical solutions and the analytical solutions(a)=10－5;(b)=10－4

为了说明本文方法的正确性，考虑受均布力作用两端简支弹性梁的弯曲问题．在小变形的情况下可得挠度的解析解．图2(a)示出了均布力p=10－5，布点数为N=7时，所得DQ数值解和解析解的比较，两者非常吻合．图2(b)示出了均布力p=10－4，布点数为N=7，9时，DQ 数 值解和解析解的比较．可以看到，当均布力增大时，线弹性小变形理论不再适用，由于非线性的影响，DQ数值解略小于解析解．由图2(b)还看到，DQ数值解的收敛性很好．

4 孔隙热弹性梁的DQ数值结果与气弹性特性分析

现在考察横向动载荷作用和气动力同时作用下孔隙热弹性梁的动力学特性，按照Chebyshev零点在梁的中性轴上布置N=15节点．并取材料参数为［13－14］:β1=0．1，h=0．1，a3=0．32，a4=12．0，a5=0．75，a6=0．6，a7=0，a8=0．5，a9=0．0804，a10=1．0 ×10－8，a11=4．0 ×106．

4．1 梁的动力学特性

首先考察两种不同类型的简单动载荷，即(1)Heaviside载荷:(a)(τ)= － 1．0 ×10－4，τ≥0;(b)(τ)= －1．0 ×10－3，τ≥0．(2)正弦载荷:(a)(τ)= －1．0 ×10－3× s in(2πτ)，τ≥0;(b)(τ)= －1．2 ×10－2×sin(2πτ)，τ≥0．图3～图4和图5～图6分别示出了在Heaviside载荷和正弦载荷作用下梁中点处变量的时程曲线和相图．可见，动载荷的类型对梁的力学行为的影响是明显的．

计算中，我们也研究了四种材料梁(即孔隙热弹性梁(TEVB)、无孔隙热弹性梁(TEB)、孔隙弹性梁(EVB)和无孔隙弹性梁(EB))的动力学特性和(7)中参数的影响，限于篇幅不再一一列出．总的结论是:孔隙的存在使梁的挠度增加．特别是位移－孔隙耦合参数主要引起挠度和孔隙力矩的变化，对温度力矩的影响不太明显;位移－热耦合参数主要引起挠度和温度力矩的变化，对孔隙力矩也有一定的影响;孔隙－热耦合参数主要引起孔隙力矩和温度力矩的变化，对挠度影响较小．梁的挠度随参数a1，a3，a5的增加而增加，但随参数a2，a4，a8的增加而减小;其他参数对梁的挠度影响均比较小．在动力学情形下，由于外力的功部分转化为热能被耗散，温度对挠度和孔隙力矩的影响不像静力学情形那样明显．

图3 梁中点处变量的时程曲线和相图()= －1．0 ×10 －4，τ≥0)(a)挠度的时程曲线;(b)挠度的相图;(c)孔隙百分比力矩时程曲线;(d)温度力矩时程曲线Fig．3 The time－history curves and the phase portrait at the midpoint()= －1．0 ×10 －4，τ≥0)(a)The time－history curves of the deflection;(b)The phase portrait of the deflection;(c)The time－history curves of the void moment;(d)The time－history curves of the temperature moment

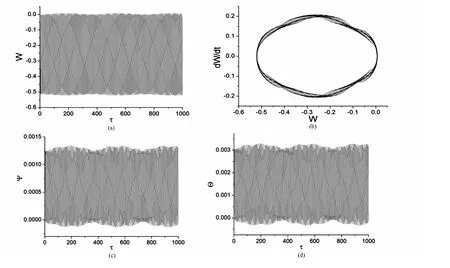
图4 梁中点处变量的时程曲线和相图)= －1．0 ×10 －3，τ≥0)(a)挠度的时程曲线;(b)挠度的相图;(c)孔隙百分比力矩时程曲线;(d)温度力矩时程曲线Fig．4 The time－history curves and the phase portrait at the midpoint= －1．0 ×10 －3，τ≥0)(a)The time－history curves of the deflection;(b)The phase portrait of the deflection;(c)The time－history curves of the void moment;(d)The time－history curves of the temperature moment

图5 梁中点处变量的时程曲线和相图= －1．0 ×10－3×sin(2πτ)，τ≥0)(a)时程曲线;(b)相图Fig．5 The time－history curves and the phase portrait at the midpoint(p(τ)= －1．0 ×10－3×sin(2πτ)，τ≥0)(a)The time－history curves;(b)The phase portrait

图6 梁中点处变量的时程曲线和相图= －1．2 ×10－2×sin(2πτ)，τ≥0)(a)时程曲线;(b)相图Fig．6 The time－history curves and the phase portrait at the midpoint()= －1．2 ×10－2×sin(2πτ)，τ≥0)(a)The time－history curves;(b)The phase portrait

4．2 梁的气弹性特性

图7 挠度的动力学特性(Q∞=2．365×10－3)(a)时程曲线;(b)功率谱;(c)相图;(d)Poincare截面Fig．7 Aerodynamic characteristics of the deflection(Q∞ =2．365×10－3)(a)Time－history curve;(b)Power spectrum;(c)Phase portrait;(d)Poincar＇e map

图8 挠度的动力学特性(Q∞=4．063×10－3)(a)时程曲线;(b)功率谱;(c)相图;(d)Poincare截面Fig．8 Aerodynamic characteristics of the deflection(Q∞ =4．063×10－3)(a)Time－history curve;(b)Power spectrum;(c)Phase portrait;(d)Poincar＇e map

图9 挠度的动力学特性(Q∞=4．096×10－3)(a)时程曲线;(b)功率谱;(c)相图;(d)Poincare截面Fig．9 Aerodynamic characteristics of the deflection(Q∞ =4．096×10－3)(a)Time－history curve;(b)Power spectrum;(c)Phase portrait;(d)Poincar＇e map

给定= －10－4× sin(2πτ)，轴力N0=10－4，图7～图10给出了不同气动压Q∞条件下挠度的时程曲线、功率谱、相图和Poincare映射．可见，当自由流的动压力逐渐增强时，Poincare映射点集由落在一个点上演变成许多个无规则的点，而且数值越来越大，结合相应的相图知，系统由周期运动转化为混沌运动．当气动压超过4．096×10－3时，点集并不被吸引到一个有界区域，而是发散到无穷．

图11给出了Q∞=4．007 ×10－3，梁中点的初始挠度分别为w0= －0．01，0．01时的时程曲线，可见，该状态由于存在多个渐进稳定的平衡点，即使在相同的系统参数下，当初值不同时，轨线趋于不同的稳定的平衡点，这是由于几何非线性所致．

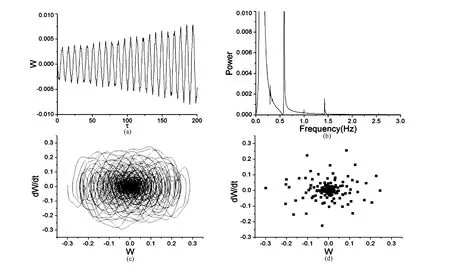
图10 挠度的动力学特性(Q∞=4．121×10－3)(a)时程曲线;(b)功率谱;(c)相图;(d)Poincare截面Fig．10 Aerodynamic characteristics of the deflection(Q∞ =4．121×10－3)(a)Time－history curve;(b)Power spectrum;(c)Phase portrait;(d)Poincar＇e map

图11 不同初始挠度下挠度的时程曲线(a)w0=－0．01;(b)w0=0．01Fig．11 The time－history curves of the deflection for different initial values(a)w0= －0．01;(b)w0=0．01

5 结论

在本文中，首先根据文献［5］中通过Hamilton变分原理建立的有限变形孔隙热弹性梁的数学模型，并采用一阶修正线性活塞理论给出的气动力来模拟结构在超高速流动中受到的气弹性载荷，由此给出了孔隙热弹性平面固定梁在动载荷和气动力作用下的非线性数学模型．在此基础上，采用DQM对变量进行空间离散，然后采用Runge－Kutta方法对离散化动力学问题进行数值求解．为了说明本文理论和方法的正确性，研究了两端简支弹性梁的小变形平面弯曲静态弯曲问题，并与解析解进行了比较．可以看到，由DQM得到的数值解和解析解是非常吻合的，且DQ数值解的收敛性也非常好．详细考察了气动载荷作用下孔隙热弹性固定梁的气弹性行为．发现在气动力的作用下，结构具有周期的稳定运动和有界混沌、无界发散两种不稳定的运动状态．与无气动力作用的孔隙热弹性梁相比，在气动力作用下孔隙热弹性梁更容易发生无界不稳定的现象．同时，增加自由流动压Q∞会降低孔隙热弹性梁的稳定性．

1 Goodman M A，Cowin S C．A continuum theory for granular materials．Archive for Rational Mechanics and Analysis，1972，44(4):249 ～266

2 Nunziato J W，Cowin S C．Nonlinear theory of elastic materials with voids．Archive for Rational Mechanics and Analy－sis，1979，72(2):175 ～201

3 Cowin S C，Nunziato J W．Linear elastic materials with voids．Journal of Elasticity，1983，13(2):125 ～147

4 Iesan D．A theory of thermoelastic materials with voids．Acta Mechanica，1986，60(1－2):67～89

5 Li Y，Cheng C J．A nonlinear model of thermoelastic beams with voids and its applications．Journal of Mechanics of Materials and Structures，2010，5(5):805 ～820

6 伏欣．气动弹性力学原理．沈克扬译．上海:上海科学技术文献出版社，1982(Forsching H W．Grundlagen der aeroelastik． S pringer－Verlag， B erlin， H eidelberg， N ew York，1974)

7 Mei C，AbdeI－Motagaly K，Chen R．Review of nonlinear panel flutter at supersonic and hypersonic speeds．Applied Mechanics Reviews，1999，52(10):321 ～ 3 32

8 Bellmam R E，Casti J．Differential quadrature and long term integration．Journal of Mathematical Analysis and Applications，1971，34(2):235 ～238

9 Bellmam R E，Kashef B G，Casti J．Differential quadrature:a technique for the rapid solution of nonlinear partial differential equations．Journal of Computational Physics，1972，10(1):40～52

10 Bert C W，Jang S K，Striz A J．Two new approximate methods for analyzing free vibtation of structural components．American Institute of Aeronautics and Astronautics Journal，1988，26(5):612 ～618

11 Bert C W，Malik M．Differential quadrature method in computational mechanics:a review．Applied Mechanics Reviews，1996，49(1):1 ～27

12 李鹏，杨翊仁，鲁丽．微分求积法分析二维亚音速壁板的失稳问题．动力学与控制学报，2012，10(1):11～14(Li P，Yang Y R，Lu L．Instability analysis of two dimensional thin panels in subsonic flow with differential quadrature method．Journal of Dynamics and Control，2012，10(1):11～14(in Chinese))

13 Puri P，Cowin S C．Plane waves in linear elastic materials with voids．Journal of Elasticity，1985，15(2):167～183

14 Kumar R，Rani L．Interaction due to mechanical and thermal sources in thermoelastic half－space with voids．Journal of Vibration and Control，2005，11(4):499～517

* The project supported by Innovation Program of Shanghai Municipal Education Commission(12YZ074)

† Corresponding author E－mail:yuanyuan_zhu@hotmail．com

NONLINEAR AEROELASTIC CHARACTERISTIC OF A THERMOELASTIC BEAM WITH VOIDS*

Zhu Yuanyuan1†Li Ying2Cheng Changjun2
(1．Department of Computer Science and Technology，Shanghai Normal University，Shanghai200234，China)(2．Department of Mechanics，Shanghai University，Shanghai200072，China)

In this study，based on the complete nonlinear mathematical model obtained from the generalized Hamilton principle of isotropic thermoelastic beams with voids and the aerodynamic pressure loading presented by the first order modified piston theory，the governing differential equations and the deterministic conditions of solutions for a thermoelastic beam with fixed ends and located in a high－speed or an ultra－high speed flow are presented，which are expressed by the axial and lateral displacements and the two“moments”defined by changes of the volume fraction of voids and the temperature field．In order to consider the nonlinear aeroelastic characteristic of the thermoelastic beam with voids subjected to the transverse loading and aerodynamic pressure loading，the differential quadrature method is applied to discretize the governing differential equations on the spatial domains，and a system of ordinary differential equations with respect to time is yielded and solved through the fourth－order Runge－Kutta method．From this，the aeroelastic characteristic of the beam is studied and the effect of parameters is considered as well．

thermoelastic beam with voids， finite deformation， the first order modified piston， differential quadrature method，aeroelastic characteristic

10 July 2012，

5 August 2012．

10．6052/1672－6553－2013－047

2012－07－10 收到第 1 稿，2012－08－05 收到修改稿．

*上海市教委创新基金资助项目(12YZ074)

E－mail:yuanyuan_zhu@hotmail．com