使用改进混沌神经网络的母线负荷预测

郭精人，罗滇生，程义明，廖 峰，蔡剑彪

（1.湖南大学 电气与信息工程学院，长沙 410082；2．景德镇供电公司，江西 景德镇 333000；3．佛山供电局，广东 佛山 528000）

使用改进混沌神经网络的母线负荷预测

郭精人1，罗滇生1，程义明2，廖 峰3，蔡剑彪1

（1.湖南大学 电气与信息工程学院，长沙 410082；2．景德镇供电公司，江西 景德镇 333000；3．佛山供电局，广东 佛山 528000）

针对母线负荷非线性、冲击性波动、有较多“毛刺”、含有较多坏数据等特点，提出了一种基于小波变换和混沌神经网络的母线负荷预测方法。该方法通过消除坏数据和噪声对负荷混沌特性分析的影响，能有效提高母线负荷预测的精度。首先对历史数据进行改进的小波阈值去噪，然后对其进行混沌特性分析，重构相空间形成训练样本，最后采用改进的混沌学习算法对网络进行训练。通过对某省某地220 kV母线负荷算例分析，显示该方法能显著提高母线负荷预测的精度。

母线负荷预测；小波去噪；相空间重构；混沌神经网络

母线负荷定义为由变电站的主变压器供给的相对较小的供电区域的终端负荷的总和[1]。短期母线负荷预测作为分析和预测电网各节点电力需求的技术支持，是其中重要的组成部分。母线负荷预测是制定电力系统运行方式的重要依据，精确的母线负荷预测是合理安排生产调度计划，保证电力系统安全、经济运行的前提和保障，提高母线负荷预测精度是实现调度精细化管理的前提[2]。

目前短期母线负荷预测主要有2类[1]方法：一类是基于系统负荷分配的预测方法[3—4]。该类方法的思路是由系统负荷预测取得某一时刻系统负荷值，然后将其分配到每一条母线上；另一类是基于节点负荷自身变化规律的预测方法[5—8]。与系统负荷分析过程类似，采用系统负荷预测的某些方法进行母线负荷预测是目前提高母线负荷预测精度常用的方法。

在实际的电网运行中，母线分布范围广泛，供电结构变化多样，母线负荷曲线比系统负荷更为复杂，大量母线负荷序列具有非线性、非平稳锯齿波动；有些母线中含有的小水电负荷，使得母线负荷曲线中有大量的毛刺；高铁沿线牵引变的随机性冲击负荷；SCADA系统采集数据时产生的随机干扰数据导致历史数据中含有很多坏数据，这些对提高母线负荷预测的精度带来了新的挑战。传统预测算法在提高系统负荷预测精度上取得了比较满意的效果，但在规律性不强的母线负荷预测中，预测精度常常会受到较大的影响。针对母线负荷的这些特点，本文提出了一种基于小波变换和混沌神经网络母线负荷预测方法。该方法首先通过改进的小波变换阈值法对原始母线负荷序列进行去噪预处理，从而能从看似无序的负荷序列的分析中发现其混沌特性。然后将最新的混沌理论和人工智能方法中的神经网络相结合用于母线负荷预测，预测效果明显优于传统的单一预测方法。本文方法已成功应用于南方某省电网母线负荷预测系统中，实践证明该方法能显著提高母线负荷预测的精度。

1 小波变换原理

1.1 小波变换

小波变换[1,9]是指用合适的母小波通过时间轴上的位移、放缩和幅度的变化，产生一系列的派生小波，用这一系列小波对所要分析的信号进行时间轴上的平移比较，获得用以表征信号与小波相似程度的小波系数。经小波平移和伸缩变换处理后的信号，可在时频域对其局部细节进行多分辨分析。

小波变换的变换因子一般由连续小波函数给出

式中：Ψ(t)∈L2(R)；a为伸缩尺度；b为平移尺度。

若Ψ(t)满足可允许性条件

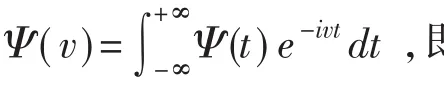
其逆变换为

具体小波函数的选取要根据被分析的函数f，并且有相关的算法。其中，一系列子小波Wf(a,b)中关键是存在2个可调参数a和b，其中，a可以视为频率参数，时间轴上伸缩控制子小波的振荡频率；b视为时移参数，表示在时间轴上的平移。

1.2 小波去噪

小波变换阈值去噪方法[10—11]包括阈值函数的选取和对阈值的具体估计。常用的阈值函数有硬阈值函数和软阈值函数。

硬阈值处理的过程是

软阈值处理的过程是

式中：x为待处理小波系数；T是阈值（T＞0）；y为处理后的小波系数；sign为符号函数。

传统的阈值法在信号的奇异点处会产生伪吉布斯现象，对高斯白噪声能有较好的去噪效果，但是对有色噪声达不到去噪效果，本文结合软、硬阈值函数对其进一步改进，其阈值函数如下

式中：u∈[0 1] ，为常数。将式（7）与传统的阈值法相比，在式（5）、式（6）中，当│x│＜T时，将小波估计系数置为0，很可能把有用的信息当作噪声滤除掉了，而式（7）的改进阈值法对软硬阈值函数进行调整，对于大阈值选用固定形式阈值，对于小阈值采用SURE自适应阈值，防止了有用信息被作为噪声滤除掉，能有效地提高去噪的效果。

2 混沌神经网络模型

2.1 基相空间重构[12—14]

假设观测得到系统某一分量的混沌负荷时间序列为{ }

x(k),k=1,2,…,N，那么在状态空间中重构的一点的状态矢量可以表示为

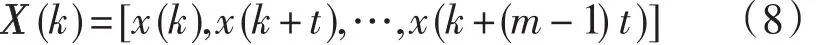
式中：m和t分别为系统的嵌入维数和延迟时间。

在相空间重构中延迟时间和嵌入维数的选择至关重要，这2个参数的合理选择和优化直接关系到所逼近的吸引子的真实性和可靠性。

2.1.1 延迟时间的选择

最佳延迟时间的选取方法主要有：自相关法，复自相关法，互信息法，奇异值分数法等。相对于其它方法，自相关函数法是较常用的求时间延迟t的方法，其特点是简便易行，计算量较小。

自相关函数法是常用的求时间延迟t的方法，它主要是提取序列的线性相关性。对于长度为n的时间序列，时间跨度为弦的自相关函数为延迟时间t，取为自相关函数第一次经过零点时对应的时间，这样能保证各嵌入坐标间相关性最小。当自相关函数下降到初始值的1-时，所对应的时间为重构相空间的延迟时间。它适用于大部分数据量较少的序列。

2.1.2 嵌入维数的选择

最佳嵌入维数的选取方法主要有：关联指数饱和法，奇异值分解法（SVD），假近邻法，改进的假近邻法等。G⁃P算法通过拟合嵌入维数与关联维数的关系使得选取更为直观、准确，是计算重构相空间嵌入维数的一个常用的方法，具体步骤如下：

利用负荷序列x1,x2,…,xn-1,xn,先给定一个较

式中：dij为Yi与Yj的欧式距离；M为相点数；θ(x)是Heaviside函数，若x＜0，θ(x)=0，若x＞0，θ(x)=1；C(r)是相空间中吸引子上2点之间的距离小于r的概率。对于r的某个适当范围，吸引子的维数D与累积分布函数C(r)应满足对数线性关系，即

由拟合求出对应于m0的关联维数估计值D(m0)。增加嵌入维数m1＞m0，重复计算式（9）和式（10），直到相应的维数估计值D(m)不再随m的增长而增长，而逐渐收敛以一个定值D，即为吸引子的关联维数。再选择合适的嵌入维m，使得m≥2D+1 。

2.2 最大Lyapunov指数的确定

负荷时间序列是否具有混沌特性取决于最大Lyapunov指数是否大于0。Wolf等人提出了用基于相轨线演化的方法来估计最大Lyapunov指数。

重构相空间。取初始相点Y(t0)，设Y′(t0)为其最邻近的相点，计算距离L(t0)给定一演化延迟时间t，得到Y(t0)的演化状态向量Y(t0+t)，Y′(t0)的演化状态向量Y′(t0+t)，计算距离 L′(t0)在t1=t处找Y′(t1)追踪并计算L(t1)、L′(t1)。重复此过程m次,计算出最大Lyapunov指数λ为小的值m1，以及某一距离阈值r；对应一个重构的相空间，则嵌入时间序列的关联积分定义为以下函数

2.3 混沌神经网络算法的改进

采用混沌理论对负荷时间序列进行相空间重构，可以确定混沌神经网络的模型结构。常见的混沌BP神经网络[15]一般都采用梯度下降法进行训练，但是其收敛速度慢，容易陷入局部最小。本文采用变尺度的混沌学习算法，能很好地克服梯度下降法的缺点。

混沌学习算法[16]计算步骤如下：

（1）初始化：由Logistic方程产xk+1=axk(1-xk)，xk∈[0 1]生n个混沌变量x（0），并把混沌变量线形映射到优化变量的取值区间，得到x*=x*(0)，作为初始权值和阈值，k=0。

（2）取x（k）的混沌变量，经过用Logistic映射到优化变量x（k+1），进而采用标准的BP算法可得到当前的优化变量x*（k+1）。

（3）如果目标函数E(x*(k+1))＜E(x*(k))，则最优变量x*=x*（k+1），否则，进行下一步迭代。

（4）如果经过N步迭代搜索后，最优函数值和最优变量没有发生改变，则转步骤（5），否则继续迭代搜索。

（5）缩小各变量的优化范围为使新的取值范围不至于越界，需要做越界处理。

（6）如果满足停止条件，则停止搜索，否则继续转入步骤（2），进行下一步计算。

2.4 混沌神经网络模型的预测流程

本文以改进的混沌神经网络为预测模型。由于预测的是下网负荷，选取母线历史负荷数据时要规避有检修、转供负荷的日期。具体的预测流程如图1所示。

图1 母线负荷预测流程

3 算例分析

本文以南方某省某变电站220 kV母线负荷（标记为母线1）作为预测对象。该母线负荷类型包括110 kV高铁负荷、工业负荷以及一部分居民生活负荷。高铁冲击负荷使得其日负荷特性规律性不明显，负荷曲线变化剧烈，给负荷预测增加了一定的难度。

3.1 小波去噪

选取db4正交小波对母线1历史负荷序列进行5层小波分解，得到低频分量和各高频分量。对低频分量不予以处理，对各高频分量采用本文的改进阈值法进行消噪。再对各个分量进行小波重构，把得到的数据作为样本。消噪前后的母线周负荷曲线如图2所示。

3.2 混沌特性分析

对该母线负荷序列由自相关函数法依次取t值为1—100，计算I-t关系如图3所示,取自相关函数第一次达到初始值1-时的时间延迟t=12。

用G⁃P算法求m值，取t=12 s，m值依次取

图2 220 kV母线1周负荷去噪前后负荷曲线

图3 自相关函数值R(t)与时间延迟t的关系

1—15，进行关联维分析，得到如图4所示结果。将图4中的每条曲线直线段的斜率，即关联维数提取出来，得到如图5所示m-dm关系图。当m=9时，维数估计值dm在一定误差范围内保持不变，所以嵌入维数m=9。再由公式（10）算出最大Lyapunov指数λ=0.008 74＞0,说明该母线负荷序列具有混沌性。最大预测时间为1/λ≈114.42＞96，满足预测时间要求。

3.3 模型建立与结果对比

图4 不同嵌入维数下lnr与lnC(r)的关系图

图5 关联维数D(m)与嵌入维数m的关系

选取母线1于2011年4月1日至2011年4月16日的负荷序列，经过去噪预处理后，重构负荷维相空间，选择1 520个相点作为神经网络的训练样本，建立混沌神经网络模型。该模型结构为9-17-1，网络输出为2011年4月17日的母线负荷，预测的预报期为1天96个点。为了比较本方法的预测效果，另选3种方法作为对比。方法1采用灰色模型进行预测；方法2采用线性回归模型进行预测；方法3采用标准BP神经网络方法进行预测。其预测准确率统计如表1所示。

表1 母线负荷预测准确率对比 %

根据国家电网公司母线负荷预测考核的有关规定，母线负荷预测准确率如下

式中：N取96；Ek为k时段的引用误差。计算方法如下

式中：Pf为预测值；Ph为负荷实际值；PB为负荷基准值，取305 MW。

图6为本文方法对母线1的日负荷预测值与实际值的比较和误差曲线图。由图6和表1可以发现，上述算法在去噪后的预测准确率明显比去噪前高，说明了噪声和坏数据对负荷预测精度的影响。和其它3种方法相比，本文的基于小波变换和混沌神经网络方法能显著提高负荷预测的精度，预测效果明显好于其它预测方法，且误差都控制在5%以内。

图6 220 kV母线1在2011年4月17日的母线负荷

4 结论

（1）通过上述对母线负荷混沌特性的分析，求得其最大Lyapunov指数为正，说明电力系统母线负荷具有混沌特性。

（2）如何合理找出最佳嵌入维数和延迟时间对预测的精度影响很大，是混沌分析的关键。本文采用简单易行、计算量小的自相关法和直观、准确的G⁃P算法能很好地满足混沌分析的要求。

（3）由于混沌系统对噪声比较敏感，采用小波变换软硬结合阈值法消除噪声和坏数据，有效地提高了母线负荷预测的精度。

（4）将最新的混沌理论与人工智能中的神经网络相结合的方法引入负荷预测中，能有效、稳定地提高预测的精度，并且有较强的适应能力。算例分析表明该模型比标准BP神经网络预测精度有明显的提高，更高于其它传统预测方法。

：

[1]康重庆，夏清，刘梅.电力系统负荷预测[M].北京：中国电力出版社，2007．

[2]赵燃，康重庆，刘梅.面向节能发电调度的母线负荷预测平台[J].中国电力,2009,42(6)：32-36.

[3]汪峰，于尔铿，周京.能量管理系统（EMS）第四讲：电力系统负荷预报[J].电力系统自动化,1997,21(4)：66-69.

[4]韩力,韩学山,贠志皓,等.多节点超短期负荷预测方法[J].电力系统自动化,2007,31(21)：30-34.

[5]焦建林，芦晶晶.基于改进时间序列法的配电网短期负荷预测模型[J].电工技术杂志，2002(5)：25-28.

[6]余贻鑫,吴建中.基于事例推理模糊神经网络的中压配电网短期节点负荷预测[J].中国电机工程学报,2005,25(12)：18-23.

[7]段欣阳.基于有色噪声的Kalman滤波算法在母线负荷预测中的应用[D].北京：华北电力大学,2008．

[8]Amjady N.Short⁃term bus load forecasting of powersystems by a new hybrid method[J].IEEE Transactions on Power Systems，2007,22(1)：33-34.

[9]彭玉华.小波变化与工程应用[M].北京：科学出版社，1999．

[10]Donoho D L,Johnstone J M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3)：425-455.

[11]Donoho D L.Denoising by soft⁃thresholding[J].IEEE Transactions on Information Theory,1995,41(3)：613-627.

[12]罗海洋，刘天齐，李兴源.风电场短期风速的混沌预测方法[J].电网技术,2009,33(9)：67-71.

[13]孙雅明，张智晟.相空间重构和混沌神经网络融合的短期负荷预测研究[J].中国电机工程学报,2004,24(1)：44-48.

[14]马轶东,何怡刚,王桓.运用BP神经网络的电力负荷混沌多步预测[J].电力系统自动化学报,2010,22(4)：81-84.

[15]程玉桂,黎明,林明玉.基于遗传算法和BP神经网络的城区中长期电力负荷预测与分析[J].计算机应用,2010,30(1)：224-226.

[16]尤勇,盛万兴,王孙安,等.一种新型短期负荷预测模型的研究及应用[J].中国电机工程学报,2002,22(9)：15-18.

Bus load forecasting using improved chaotic neural network

GUO Jing⁃ren1,LUO Dian⁃sheng1,CHENG Yi⁃ming2,LIAO Feng3,CAI Jian⁃biao1
(1.Hunan University,Changsha 410082,China；2.Jingdezhen Power Supply Company，Jingdezhen 333000，China；3.Foshan Power Supply Bureau,Foshan 528000，China)

The bus load is nonlinearity,impact fluctuation,more burrs and contain more bad data,the prediction algorithm based on the wavelet transform and chaotic neural network is pro⁃posed to set up the bus load model.This method can effectively im⁃prove the accuracy of the load forecast by eliminating bad data and noise to the influence of bus load chaotic characteristic analysis.Firstly，it de⁃noises data of load using improved wavelet threshold,then uses the reconstruction of phase space to form the training sample through chaotic characteristic analysis of it.Finally it uses the improved chaotic learning algorithm to train the neural net⁃work.Through the example analysis of the 220 kV bus load of pro⁃vincial somewhere,this method can significantly improve the bus load forecasting accuracy.

bus load forecasting;wavelet denoising;recon⁃struction of phase space;chaotic neural network

TM715

A

1009-1831（2013）01-0015-05

2012-09-17

郭精人(1987)，男，江西遂川人,硕士研究生，研究方向为电力系统负荷预测、电网规划的研究；罗滇生(1971)，男，江西遂川人，博士，教授，研究生导师，主要从事负荷预测、电力市场理论及其应用、电力系统在线监测方面的研究；程义明(1986)，男，江西景德镇人，硕士研究生，研究方向为电力系统负荷预测、电网规划；廖峰(1985)，男，福建南平人，硕士研究生，主要从事电力系统软件开发、负荷预测及电网规划方面研究；蔡剑彪(1987)，男，浙江杭州人，硕士研究生，从事电力系统软件开发、负荷预测的研究。

国家自然科学基金项目(51277057);湖南省自然科学基金委员会与衡阳市政府自然科学联合基金资助（11JJ8003）

（

杜先波）