地区电网降温负荷与气温的敏感性分析

何晓峰，黄 媚，农植贵，龙裕芳，何奉禄，卢 艺

（1.深圳供电局有限公司 电力调度控制中心，广东 深圳 518001；2.广西大学 电气工程学院，南宁 530004；3.广州市奔流电力科技有限公司，广州 510640）

地区电网降温负荷与气温的敏感性分析

何晓峰1，黄 媚1，农植贵2，龙裕芳2，何奉禄3，卢 艺1

（1.深圳供电局有限公司 电力调度控制中心，广东 深圳 518001；2.广西大学 电气工程学院，南宁 530004；3.广州市奔流电力科技有限公司，广州 510640）

采用最大负荷比较法，对比了4种基准负荷的选择方法，依据实际电网的负荷数据，选择实际负荷减去基础负荷后得到的降温负荷与实际值最接近的情况所对应的基础负荷作为最终方案，建立了降温负荷与气温的敏感性高阶回归模型，据此获得降温负荷受气温影响的规律。将该方法应用于深圳电网降温负荷与气温的敏感性分析，得到相应的变化规律，获得深圳电网降温负荷的测算方法，为电网的生产调度、优化运行和营销工作提供重要参考依据。

降温负荷；气温敏感性；回归分析；负荷预测

随着国民经济的快速发展和人民生活质量的不断提高，电网负荷水平和结构发生了很大变化。在一些夏季炎热且持续高温的地区，空调等降温负荷已经成为夏季电网负荷屡创新高和影响其负荷波动的主要原因之一。因此，准确地把握地区电网夏季降温负荷与气温的敏感性变化等的特殊规律，对电网的生产调度、安全优化运行及规划设计具有重要意义。从短期看，其将为电网制定“迎峰度夏”措施提供科学依据；从长期看，其更是智能电网框架下挖掘需求响应资源、制定有效需求响应措施的必要前提[1—2]。

如何准确地确定降温负荷，一直以来都是研究的关键和难点。目前，广泛应用的方法主要有最大负荷比较法[3—6]和基准负荷比较法[7—9]。最大负荷比较法一般指通过对第三季度（夏季）最大负荷与基本无降温负荷月份的最大负荷进行比较，从而确定最大降温负荷。这种方法简单，易于实现，因此，本文选取最大负荷比较法确定降温负荷。基准负荷的选取是确定降温负荷的核心。文献[3—6]直接选取春、秋两季基准月的日最大负荷均值作为基准负荷，这种选取方法没有统一的评判标准，难以判断基准月选取的效果。基于此，本文对比了4种基准负荷的选择方法，将其作为候选方法分别应用于地区电网的基础数据，选取所得到的降温负荷天数与实际降温负荷发生天数最接近的基准负荷作为最终的基准负荷；建立了降温负荷和气温的高阶回归模型，更好地拟合自变量与因变量之间的非线性关系，获得反映地区电网降温负荷受气温影响的规律。最后，以深圳电网2012年的负荷数据为实际应用，得到深圳电网降温负荷与气象的回归关系，据此测算其降温负荷，从而指导深圳电网安全经济生产和调度运行。

1 最大降温负荷的确定

本文选取最大负荷比较法[3]进行研究，通过对比第三季度（夏季）最大负荷与基本无降温负荷月份的最大负荷，确定最大降温负荷。

1.1 最大降温负荷测算过程

最大降温负荷的测算过程如下：

（1）确定比较月：一般选取降温负荷最大的月份，例如：第三季度（夏季）最大负荷对应的月份。

（2）确定基准负荷：一般选取气候比较凉爽、降水较少的月份（称为基准月）中日最高气温低于25℃的日最大负荷平均值作为基准负荷，例如：4—5月和10—11月，这些月份除了部分工业企业存在少许降温负荷外，其他降温负荷几乎为零。

（3）比较：比较月中各天的日最大负荷与基准负荷的差值即为比较月每日的日最大降温负荷，其中的最大值为年最大降温负荷。

1.2 基准负荷的获取

从上面的步骤可知，基准月的选取至关重要，常用的选取春季或秋季作为基准月的方法，未对基准月有明确的规定，当选择不当时，则可能会导致降温负荷计算结果失准。为此，本文分别采用了4种基准负荷确定方法，将所得降温负荷发生天数与实际发生降温负荷天数最接近的负荷作为最终基准负荷。获得基准负荷的过程如下：

（1）选择某个温度作为基准温度，当某日最高气温大于基准气温，则认为该日发生降温负荷；反之，则不发生。通过研究发现，降温负荷一般发生在气温高于25℃以上[3]，因此，本文选取25℃作为基准温度。

（2）统计各月日最高气温大于基准温度的天数，作为各月份发生降温负荷的天数。

（3）选择春季中所有日最大负荷的均值最小的月、秋季中所有日最大负荷均值最小的月、全年中日最大负荷最小的月作为候选的基准月，分别称为候选基准月1、候选基准月2和候选基准月3。

（4）分别将候选基准月1、2、3中日最高气温低于25℃的日最大负荷均值作为基准负荷[3]，得到基准负荷1、基准负荷2和基准负荷3；将基准负荷1和基准负荷2的均值作为基准负荷4。

（5）将待确定最大降温负荷的样本每天的日最大负荷分别减去上述4种基准负荷，如果所得的数值为正，则认为当天发生降温负荷；反之，则不发生。

（6）统计这4种基准负荷下每月发生降温负荷的天数，并与步骤（2）中实际需要发生降温负荷的天数比较，选出最接近实际情况的负荷值作为基准负荷。

获得基准负荷后，按照最大降温负荷的测算过程（3），即可确定最大降温负荷。

2 降温负荷与气温的敏感性分析方法

为了分析气温对降温负荷的影响程度，下面采用多种回归方法分析两者的关系，选择拟合效果最佳者作为最终方案，捕捉降温负荷与气温的相关关系，拟揭示两者之间的变化规律。

2.1 回归分析模型

回归模型的定义如下[10—12]：

定义1 非线性回归模型（高阶回归模型）

设X是可控变量，Y是依赖于X的随机变量，它们的关系是

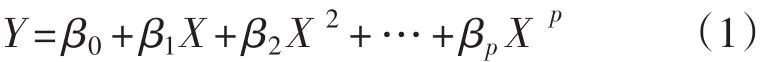
式中：p为回归模型的阶数，β=(β0,β1,…,βp)是待估计的参数。

定义2 多元线性回归模型

多项式回归模型是一元非线性回归模型的一种特殊情况，它可以通过变量代换线性化。令X1=X,X2=X2,…,Xp=Xp，多项式回归模型则变成多元线性回归模型（β同式（1））

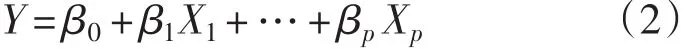
定义3 一元线性回归模型

一元线性回归模型是多元线性回归模型的特殊情况。当P=1时，式（2）即变成一元线性回归模型（β同式（1））

2.2 参数估计

本文采用最小二乘方法对参数β进行估计，获得参数β的估计值β。

由定义2可知，非线性模型回归可通过变量代换转化成多元线性回归模型，因此，本文只介绍多元线性回归模型和一元线性回归模型中参数β的估计步骤。

（1）估计多元线性回归模型参数β

为了书写方便，把多元回归模型写成矩阵形式，如式（4）所示。

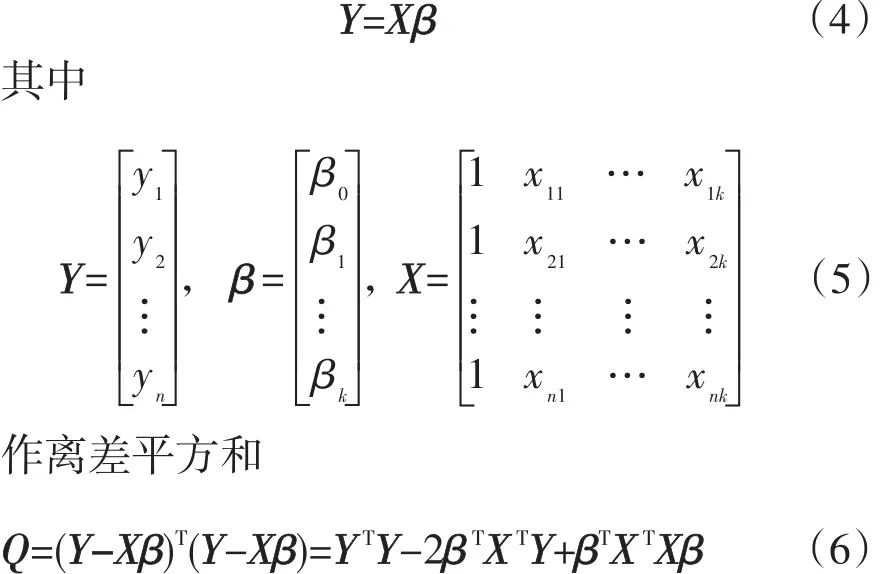
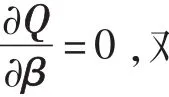
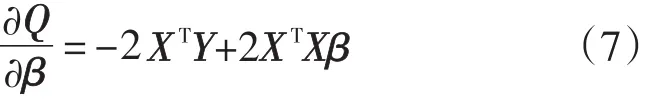
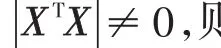
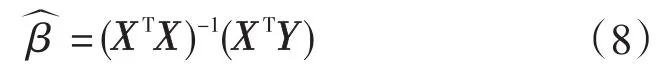
（2）估计一元线性回归模型参数β0、β1

作离差平方和

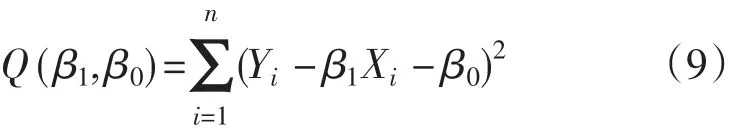
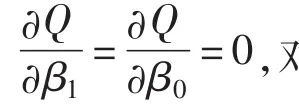
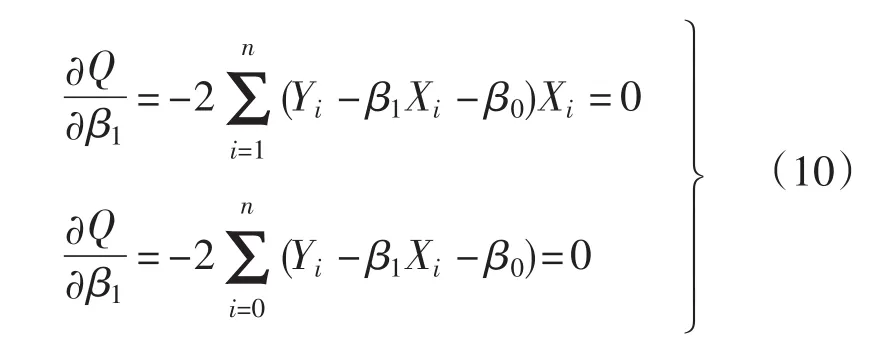
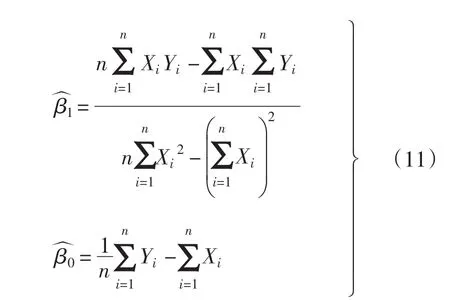
求解方程组（10），即可得到参数β0和β1的估计值，如式（11）所示

2.3 拟合相关系数

本文在分析降温负荷与气温的关系时，采用相关系数定量衡量两者之间的回归拟合程度。

利用式（12）求得各个模型拟合的相关系数。

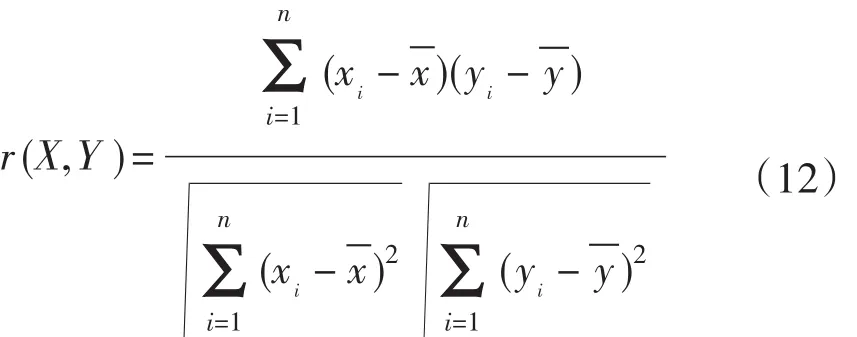
式中：和分别表示可控变量X和随机变量Y2个数列的平均值。计算结果r(X,Y)表示2数列之间相关程度的统计指标，其值介于[-1，1]区间。r(X,Y)大于0时表示正相关，小于0时表示负相关。r(X,Y)的绝对值越接近于1，两要素的关系越密切；越接近于0，两要素的关系越不密切。

2.4 基于回归分析方法的降温负荷与气温的敏感性分析

降温负荷与气温的敏感性分析中，气温因子一般选取最高气温、最低气温和平均气温。气温因子相当于回归分析法中的可控变量X，降温负荷Y是依赖于气温因子X的随机变量。基于回归分析方法的降温负荷与气温的敏感性分析的步骤如下。

（1）按最大降温负荷测算过程获得日降温负荷（E）。

（2）选取日降温负荷（E）对应于回归模型中的Y，日最高气温（Tg）、日最低气温（Td）和日平均气温（Ta）对应于回归模型中的X，对X和Y分别选用非线性回归模型、多元线性回归模型和一元线性回归模型进行拟合，根据2.2节所述方法对相应模型的参数进行估计，并按照式（12）求得各个模型的拟合相关系数。

（3）选择各个模型中拟合相关系数最大者作为最终的回归模型。

（4）求得回归模型后，把Tg、Td和Ta的值代入模型，即可获得它们相应的日降温负荷值（E），进而分析出E随Tg、Td和Ta的变化而变化的规律。

3 深圳电网最大降温负荷与气温的敏感性分析

3.1 候选基准负荷的选取

本文应用深圳市2012年剔除节假日及周末的日最大负荷及温度数据对以上方法进行仿真。依前面所述，本文分别采用全年日最大负荷均值最小的月、春季代表月、秋季代表月、春季和秋季代表月的均值作为基准月，计算深圳电网降温负荷并分析其效果。

图1为深圳市2012年日最大负荷的变化情况。

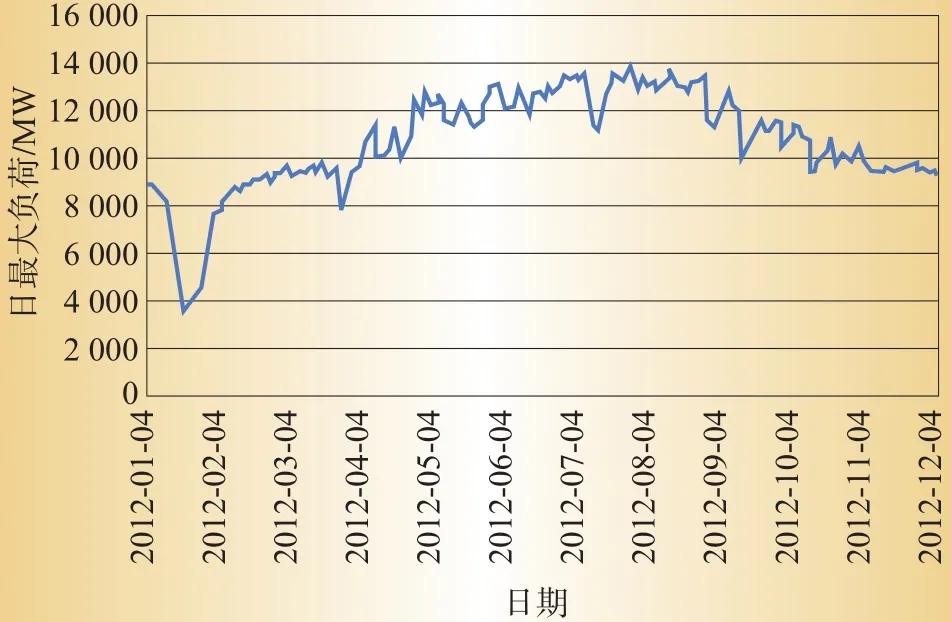
图1 2012年日最大负荷曲线图

从图1中可看出日最大负荷最低发生在1月，全年最低负荷为3 623 MW；3月至8月中旬，日最大负荷呈上升趋势，最大负荷出现在8月8日，负荷值为13 648 MW；9月中旬至12月日最大负荷呈下降趋势。从图1可初步确定：选择1—3月份中的某一个月作为基准月。

为了清楚地看出各月日最大负荷变化的情况，做出深圳电网2012年每个月的日最大负荷均值曲线图，如图2所示。

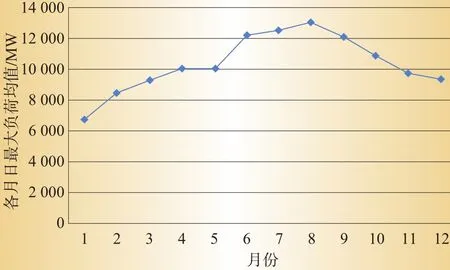
图2 2012年各月日最大负荷均值折线图

从图2中可以看出，1月为全年日最大负荷的均值最小的月份，负荷值为6 757.9 MW，春季日最大负荷均值最小发生在3月，负荷值为9 310.1 MW，秋季日最大负荷均值最小发生在11月，负荷值为9 790.8 MW。

结合上述基准月的选取方法，可选取4种方案作为深圳电网2012年的基准月：全年日最大负荷均值最小月1月、春季代表月3月、秋季代表月11月、春季代表月3月和秋季代表月11月的均值，将各基准月对应的日最大负荷作为基准负荷，如表1所示。

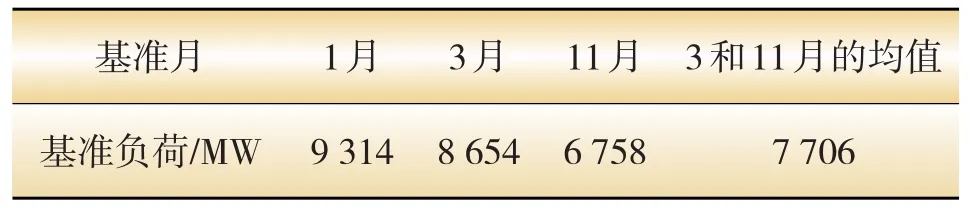
表1 不同基准月下的基准负荷

从表1可看出，秋季代表月11月的基准负荷最低，为6 758 MW；全年日最大负荷均值最小月1月的基准负荷最高，为9 314 MW。

下面通过分析对比，从中选取最佳的基准负荷。

3.2 最佳基准负荷的选取

按基准负荷的获取方法统计各月温度大于25℃的天数作为深圳电网2012年各月降温负荷实际发生的天数，结果如表2所示。

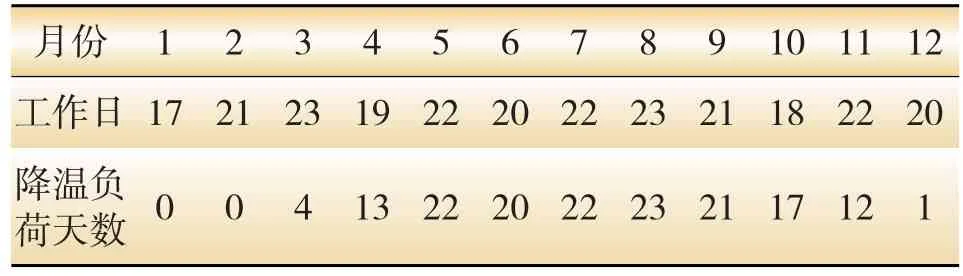
表2 各月的工作日与发生降温负荷的工作日统计

从表2可看出，1月、2月不发生降温负荷；而8月份最多，为23天，这是因为8月份气温较高，空调等降温负荷比重较大。

利用候选的基准负荷计算降温负荷，分别统计对应于各候选基准负荷发生降温负荷的天数，结果如表3所示。

表3 2012年各月在不同基准月降温负荷发生的天数天

通过对比表2和表3可知，2012年深圳降温负荷选取3月份作为基准月时，实际降温负荷发生的天数与实际最接近。

3.3 降温负荷的确定

选取3月份作为基准月，计算2012年各月的日最大负荷与基准月负荷的差值，得到每天的降温负荷，如表4所示。

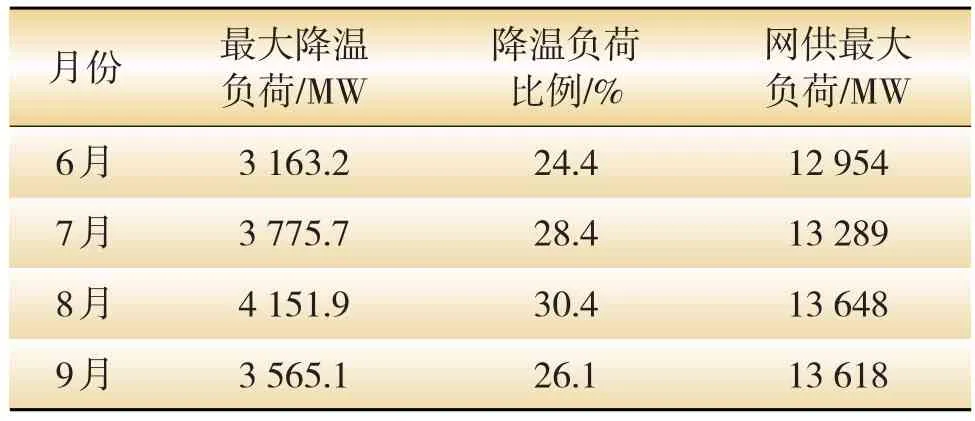
表4 2012年深圳市降温负荷所占比例

从表4可以看出，在温度低于25℃不发生降温负荷的假设下[3,4，14,15]，降温负荷比例最大发生在8月份，最大降温负荷为4 151.9 MW，峰值为13 648 MW，降温负荷所占的比例为30.4%，且最大降温负荷发生在8月9日，这是由2012年深圳市持续高温引起的。

图3为深圳电网2012年降温负荷的变化趋势示意图。从图3中可以看出，深圳电网2012年中，6—8月降温负荷的比重逐渐升高，8月份后降温负荷开始减少。

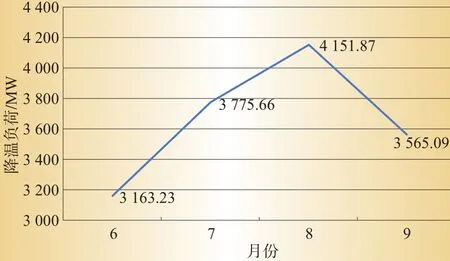
图3 深圳电网2012年降温负荷变化趋势

为了分析深圳电网逐年降温负荷的变化趋势情况，下面分别计算了2011—2012年的7—9月份各个时段的降温负荷，各个时段的降温负荷如表5所示。

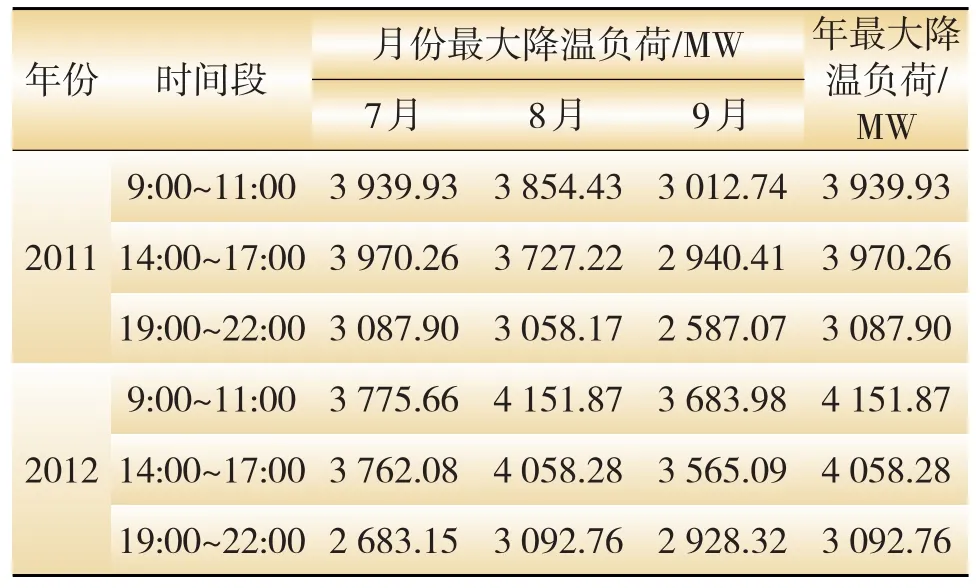
表5 深圳电网2011—2012年最大降温负荷

从表5可看出：①深圳月最大降温负荷发生在7月或8月份，且最大负荷逐步由午高峰转移到早高峰；②年最大降温负荷逐年增加，由2011年的3 970.2 MW增加至2012年的4 151.9 MW，占当年最大负荷的比重则由29.3%上升到30.4%。

3.4 深圳降温负荷与气温的敏感性分析

为了更好地分析深圳降温负荷（E）与气温的关系，本文对每日降温负荷（E）与气温进行敏感度分析。下面分别建立日降温负荷（E）与日最高气温(Tg)、日降温负荷（E）与日最低气温(Td)、日降温负荷（E）与日平均气温(Ta)的线性和非线性回归模型，建立日降温负荷与Tg、Td和Ta的多元线性回归模型。

首先做出日降温负荷与每日温度的散点图和趋势线，以便找出合适的曲线拟合变量间的关系，结果如图4所示。

从图4可以看出，日降温负荷与Tg、Td和Ta之间可以利用回归关系进行拟合。日降温负荷与Tg之间呈现非线性关系，日降温负荷与Td和Ta的关系接近于线性关系。分别采用2.1小节的3种回归模型进行拟合，得到如表6所示的结果。

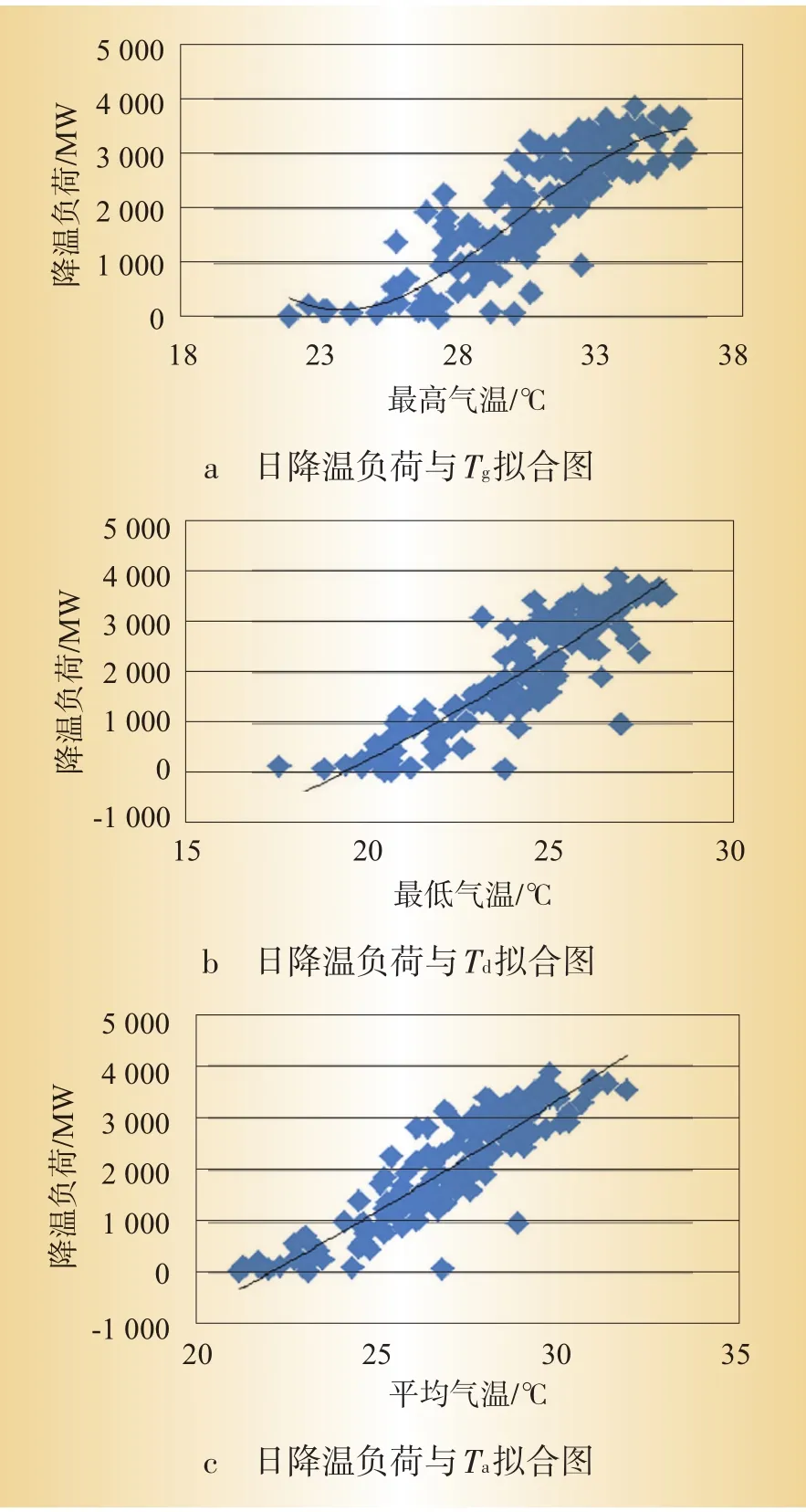
图4 降温负荷与气温的散点图及趋势线

从表6可知，在相同样本容量下，多元线性回归模型的相关系数（0.85）最高，因此Tg和Td相结合可更好地描述深圳降温负荷。从拟合式子看，对于深圳电网，当气温高于25℃时，Tg每升高1℃，负荷升高278.4 MW，Td每升高1℃，负荷升高154.9 MW。

此外，根据表6还可以看出，采用非线性回归模型拟合日降温负荷与Tg的关系时，相关系数为0.75，较采用一元线性回归描述效果好；而对于日降温负荷与Td、Ta的关系，非线性回归和一元线性回归的效果区别不大；而多元回归的效果要好于一元线性回归和非线性回归。

根据表6的线性回归拟合结果，可得到深圳电网降温负荷与气温变化的大体规律：在温度高于25℃的情况下，Tg每升高1℃，日降温负荷增加315 MW左右；在气温高于25℃的情况下，Td每升高1℃，日降温负荷增加441 MW左右；在气温高于25℃的情况下，Ta每升高1℃，日降温负荷增加419 MW左右。

根据表6的多元线性回归拟合结果，可以得到：日最高气温和日最低气温与日降温负荷的相关系数（0.85）最大，拟合效果最好。此时，深圳市降温负荷受气温影响的规律为：当日最高温度不变时，日最低温度每增加1℃，日降温负荷大约增加278.4 MW；而当最低温度不变时，日最高温度每增加1℃，日降温负荷大约增加154.9 MW。

表6 气温与降温负荷的关联函数

4 结论

本文采用最大负荷比较法确定最大降温负荷，将回归分析方法理论应用于深圳电网负荷数据，建立了深圳电网日降温负荷—气温模型，得出结论：最大降温负荷占日最高统调用电负荷的30%以上；气温高于25℃时，其每升高1℃，日降温负荷随之发生明显变化。因此，在电力需求侧管理中应对降温负荷加以重点关注，制定有效的需求响应措施，进而为电网的生产调度提供决策依据。

：

[1]陶勇,沈颖.夏季气象条件对地区空调负荷的影响[J].华东电力,2006,34(10)：29-30.

[2]糜作维.基于BP人工神经网络的空调降温负荷预测[J].电力需求侧管理，2010,12(4)：27-30．

[3]唐良艳.电力系统负荷特性分析与负荷预测研究[D].广州：华南理工大学,2010.

[4]童述林,文福拴.节能减排环境下广东省年最大降温负荷的测算与分析[J].华北电力大学学报,2010,37(5)：32-37．

[5]石峰,吴笛,李宝珠.重庆市夏季空调负荷分析及有效调节空调负荷的措施建议[J].电力技术经济,2008,20(1)：42-46.

[6]Sanhueza S,Tofoli F L,De Albuquerque F L,et al.Analysis and evaluation of residential air conditioners for power system studies[J].IEEE Transactions on Power Systems,2007,22(2)：706-716.

[7]Peng Jianchun,Jiang Hui,Song Yonghua.A weakly conditioned imputation of an impedance⁃branch dissipation power[J].IEEETransactionsonPowerSystems,2007,22(4)：2124-2133.

[8]Judith B,Cardell.Marlginal loss pricing for hours with transmission congestion[J].IEEE Transactions on Power Systems,2007,22(4)：1 466-1 474.

[9]周坚,蒋逸静,严正,等.网损因子法在华东区域电力市场的应用分析[J].电力系统自动化,2008,32(3)：76-80.

10]孙荣恒.应用数理统计[M].北京：科学出版社,2003：193-239.

[11]汪荣鑫.数理统计[M].西安：西安交通大学出版社,2012：176-180.

[12]周概荣.概率论与数理统计[M].北京：高等教育出版社,1984.

[13]Gregorczuk M,K Cena.Distribution of effective temperature over the surface of the earth[J].Bioclimateor,1967(11)：145-149.

[14]邱向京,周峰,刘升,等.福建省年最大降温负荷测算分析与研究[J].华东电力,2005,33（10）：86-90.

[15]朱振伟.气象因素对电网负荷特性影响的研究[D].杭州：浙江大学,2008：25-26.

Analysis of cooling load and temperature sensitivity on regional grid

HE Xiao⁃feng1,HUANG Mei1,NONG Zhi⁃gui2,LONG Yu⁃fang2,HE Feng⁃Lu3,LU Yi1
（1.Dispatching and Control Center of Shenzhen Power Supply Co.,Ltd,Shenzhen 518001,China;2.Guangxi University,Nanning 530004,China;3.Guangzhou Benliu Electric Power Technology Co.,Ltd.,Guangzhou 510640,China）

The comparative method of maximum load is used in this paper,comparing four reference load selection methods ap⁃plied to grid load data,selecting the reference load which result is the closest to actual cooling load as the final program.This paper establishes high⁃order regression models between the cooling load and the temperature,analyzes the cooling load influenced by tem⁃perature in Shenzhen grid,which will provide important reference for production scheduling,the optimal operation and marketing work of the grid.

cooling load;temperature sensitivity;regression analysis;load forecast

TM714

A

1009-1831（2013）05-0017-06

2013-04-22

何晓峰（1979），男，广东兴宁人，工学博士，工程师，主要从事电网运行策划分析、电网潮流分析计算和稳控装置管理方面的工作；黄媚（1979），女，广东梅州人，工学硕士，高级工程师，主要从事电网安全稳定、运行方式和电厂管理方面的研究工作；农植贵（1987），男（壮族），广西南丹人，硕士研究生，主要研究负荷特性分析、新能源并网优化运行；龙裕芳（1987），女（瑶族），广西桂林人，硕士研究生，主要研究负荷特性分析、新能源并网优化运行；何奉禄（1986），男，广东韶关人，本科，助理工程师，研发工程师，主要研究无功的优化和补偿；卢艺（1985），女，湖北宜昌人，工学硕士，工程师，主要从事电网调度与运行方式的工作。

（

杨 凯）