基于改进的TOPSIS法与RSR法的电能质量综合评估

杨志新，袁晓冬，柏晶晶

（1.江苏省电力公司 电力科学研究院，南京 210000；2.东南大学 电气工程学院，南京 210096）

基于改进的TOPSIS法与RSR法的电能质量综合评估

杨志新1，袁晓冬1，柏晶晶2

（1.江苏省电力公司 电力科学研究院，南京 210000；2.东南大学 电气工程学院，南京 210096）

对电能质量各项指标进行综合评估，可量化现有各层面电能质量状况，便于实现电力市场的按质定价。利用改进的层次分析法和主成分分析法确定各指标的组合权重，同时将改进的逼近理想解排序（TOPSIS）法与秩和比（RSR）法应用于电能质量综合评估，将观测点电能质量状况与理想解、国标允许值和自设的等级值结合到一起进行排序和分档，从而快速实现电能质量综合评估。实例计算结果表明，采用上述方法具有一定的有效性和可行性。

电能质量；综合评估；主成分分析；改进TOPSIS；RSR

对电能质量综合评估，其结果一方面可作为衡量电网水平重要标准，为明确供电合同中供电方和用户责任提供数据支持，也便于实现电力市场的按质定价；另一方面，供电方可以全面掌握电网电能质量状况，对电能质量问题做到“早发现，早治理”，防止电能质量问题恶化；而敏感用户通过查看报表、图形化的评估结果，可更清楚了解用电状况，及时做出生产调整。

由于电能质量是一个多指标的有机集合，单纯依据某个指标对电能质量进行评估，不能全面、科学地体现整体的电能质量水平状况，因此需要对电能质量进行综合评估[1]。对于这种问题，国内已有较多文献进行了相关研究。

文献[2]基于概率统计特征值方法，并采用矢量代数方法可有效地将不同电能质量分项指标归一量化，使电能商品的优质和优价对应成为可能。但是若相应基准值选取不当，会对电能质量综合评估准确性产生很大影响。文献[3]采用模糊综合评价方法，其主要依靠经验近似获得隶属度函数及其权重，主观因素影响偏大。文献[4]应用物元分析理论对电能质量进行综合评估，利用关联度信息对电能质量的等级进行可拓识别，效果较好。文献[5]基于人工神经网络进行电能质量评估，使用客观样本进行训练，避免了主观因素的影响，但因缺乏了解电能质量分项指标各自具体所占权重情况，使得评估结果可信度降低。

在对上述评估方法分析的基础上，本文将改进的逼近理想解排序法（TOPSIS）与秩和比法（RSR）相结合，应用于电能质量综合评估及分级评估，从而可将观测点电能质量状况与理想解、国标允许值和自设的等级临界值结合在一起进行排序和分档，使得结果不但可快速实现电能质量定性评价，而且能通过等级评分函数对电能质量进行定量评估。

1 电能质量评估指标及权重的确定

1.1 电能质量评估指标

本文拟以表1中的9项电能质量指标为基础，依照国家标准或国际公认定义的规定范围，将电能质量等级评定分为5级，对应为优质Q1、良好Q2、中等Q3、合格Q4、不合格Q5，从Q1～Q5，电能质量情况逐级下降[6]，这样既避免了因分级太少导致计算过程偏差过大、影响评估结果的准确性，又避免了因分级过多而造成计算量大。电能质量各指标等级界限值确定方法见参考文献[3，6]，结果如表1所示。

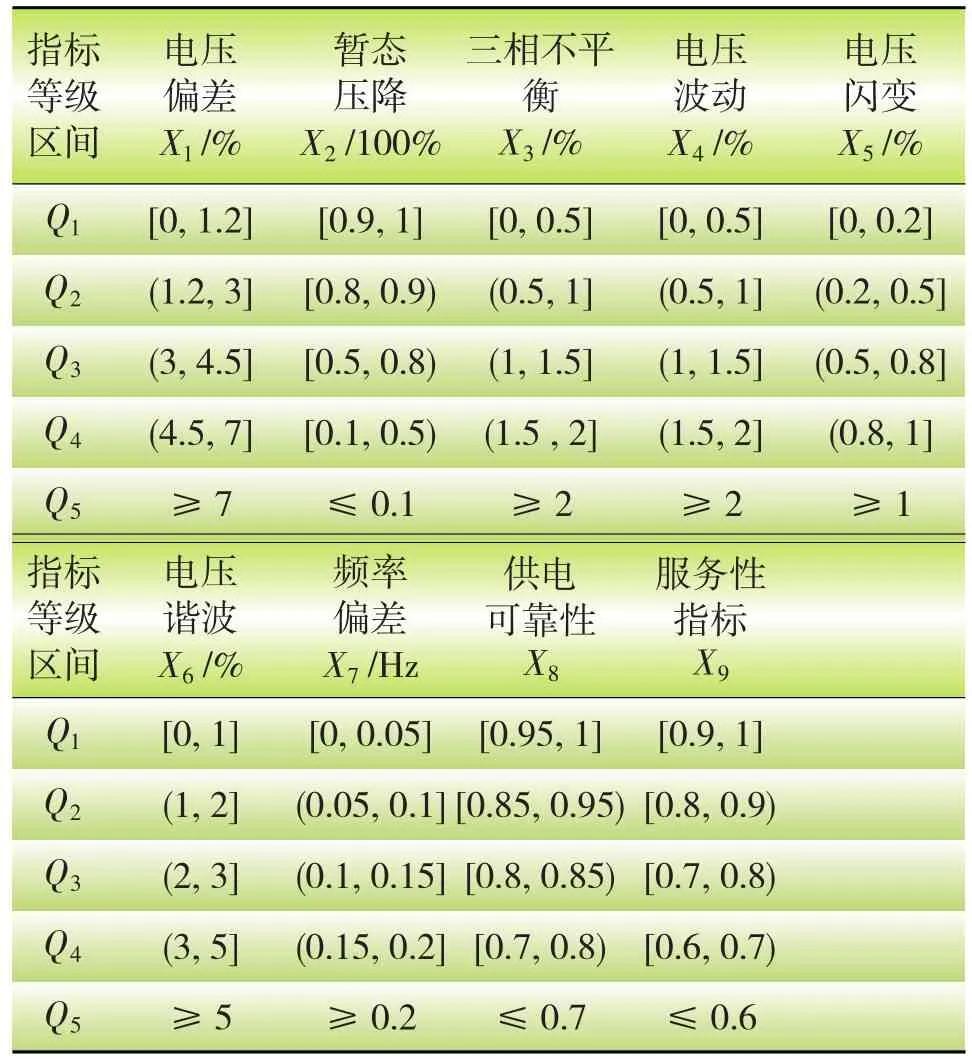
表1 电能质量指标及其分级标准(380 V)

1.2 权重确定

目前，权重确定方法有主观赋权法和客观赋权法两大类，它们各有优缺点[7]。主观赋权是一种定性分析法，是根据实际情况并通过专家经验判断指标的重要程度，但这样就增加了人为主观因素影响；客观赋权则是依据原始数据确定权重系数，虽可有效地传递评价指标的数据与信息，但其可能因此出现权重系数不合理现象。为避免单一方式定权而造成权重系数的偏倚，本文将采用主客观权重线性加权确定指标综合权重，其中客观权重采用主成分分析法，主观权重采用改进的层次分析法。

1.2.1 主成分分析法确定客观权重

主成分分析（principal component analysis，PCA）是多元分析中最重要的方法之一，其是通过恰当的数学变换，使新变量——主成分成为原变量的线性组合[8—9]。其赋权的基本思想是：根据各项指标值的变异程度选取主成分，提取其中少数几个在变差总信息量中比例较大的主成分来分析事物的特征，再依据其特征向量进行综合值评价，从而可依据综合值的各系数比重确定各指标权重。

下面分析PCA计算权重的具体步骤。

（1）设对某一评价对象进行评估时，原始数据表中样本数为n，指标数为p，则观测样本矩阵为

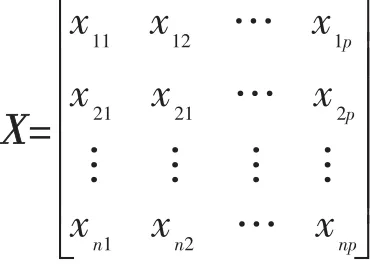
在实际应用中，为了消除原变量量纲、数量级的不同带来的影响，通常需对各变量作标准化变换，其变换公式为

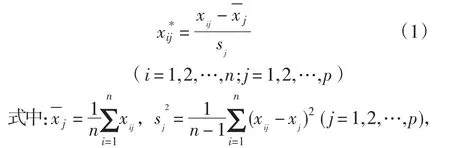
经过变换后的数据均值为0，方差为1。

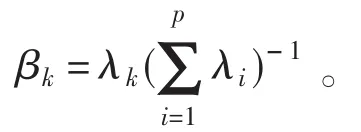
（3）将步骤（2）计算得到的p个特征值按从大到小的顺序排列，并从中选取前m个特征值作为主成分，使得所取主成分累计方差贡献率达到85%以上，即

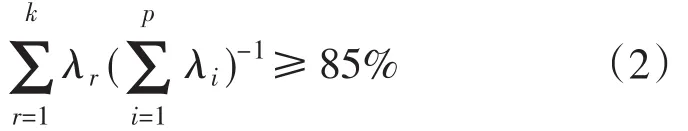
（4）按照公式（3）计算主成分综合值

式中：n为样本数，m为选取的能满足累计贡献率要求的主成分个数，λi和ui分别为选取的主成分对应的特征值和特征向量，F为计算得到的综合值，是一个列向量F=(b1,b2,…,bp)T。根据计算得到bi的大小可确定各评价指标的权重Wi

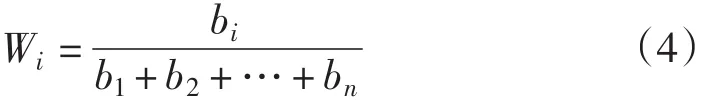
1.2.2 改进AHP法确定主观权重

普通的层次分析法（analytic hierarchy process,AHP）采用1—9标度，在实际应用中有许多欠妥之处，它可能导致评价结论的错误与一致性检验的错误[10]。本文参考文献[10]建立一种新的指标标度，使用改进AHP法确定主观权重，其具体求取过程见文献[6,10—12]，本文不再重复叙述。

1.2.3 线性求权确定组合权重

将已得到的客观权重WW1′和主观权重WW1″进行线性加权，得到各指标的综合权重向量[13]

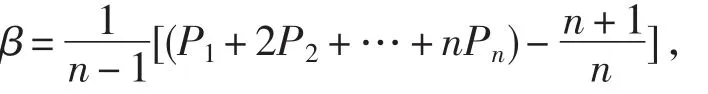
2 基于改进的TOPSIS法的电能质量综合评估

在多指标的决策问题中，TOPSIS（Technique for Order Preference by Similarityto Ideal Solution）是一种逼近理想解的排序方法，其借助于多指标问题中的正理想解和负理想解对方案集中的各方案进行排序[14—19]。常规的TOPSIS法只能对原始数据进行定性的排序[14—15]，不能进行定量的综合评估。为了克服这个缺点，本文提出了一种改进的TOPSIS法，并将其与单指标评分思想相结合，不仅可对原始数据进行综合评估，而且可以等级评分的形式对其进行分析。

下面具体分析其计算步骤。

（1）构造原始矩阵。除5个观测点数据外，本文还引入了5点参考电能指标序列，分别是各项电能指标的理想值、国标允许值和等级1、2、3临界值的数据序列。其中针对常规的TOPSIS法可能会出现的逆序问题，本文将各项电能指标的理想值和国标允许值分别作为TOPSIS法使用中的绝对正理想解和绝对负理想解，此外，为能对原始数据进行有效的分等级评估，本文还将等级1、2、3临界值的数据序列添加到评价对象的数据矩阵中一起进行运算处理。

（2）为便于后续分析，需对原始矩阵进行同趋势化处理，将指标全变为低优或高优指标，常用的方法有倒数法和插值法等。

（3）同趋势化后，为了消除计量单位的影响，需要按照公式（6）进行向量归一化处理，得到归一化矩阵ZZ。

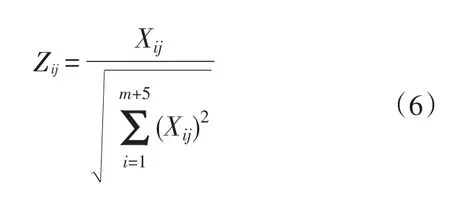
（4）为判断各样本的合格情况，需按照公式（7）计算正理想解与负理想解之间的距离D作为判断标准。

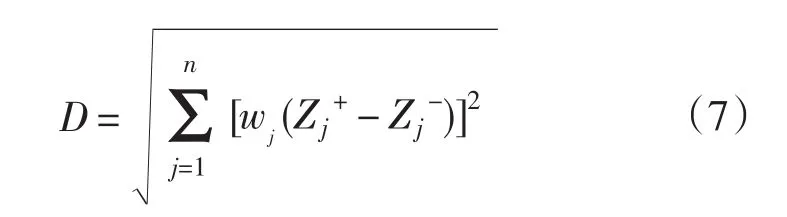
（5）按公式（8）计算各评估对象的指标值与理正理想解及负理想解之间的距离D+和D-，计算公式如下

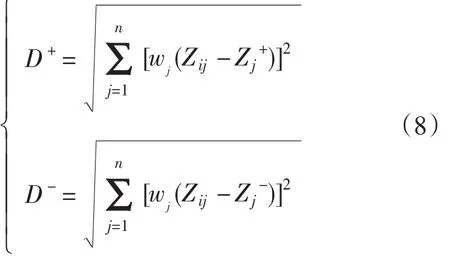
（6）为能综合评估各种电能质量情况，本文扩展了TOPSIS中贴近系数C的定义，使其不仅可定义在0～1区间，而且在大于1的时候也有定义，此时大于1的情况是对应于评估结果不合格的情形。其具体的计算公式如下

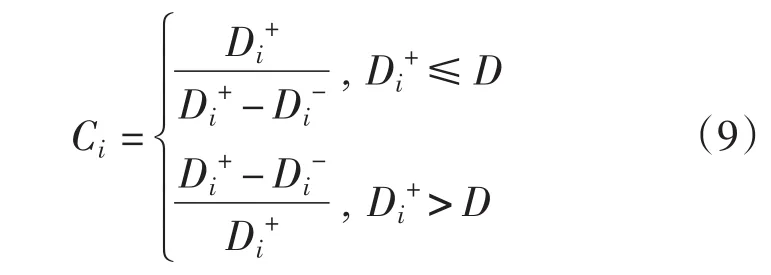
完成这一步之后，可以得到8个贴近系数，分别是C1，C2，…，C8，其中C1，C2，…，C5代表的是5个观测点的贴近系数，而C6、C7、C8代表的是为判断等级而设置的临界值。此时，若想快速判断出5个观测点电能质量状况的相对好坏，可直接根据该贴近系数进行分析，Ci值越小电能质量状况越优。另外，将各观测点的Ci与C6，C7，C8比较，也可迅速判断其所处的等级，但这只是初步的定性判断，若进一步定量分析，还需进行下面的步骤。

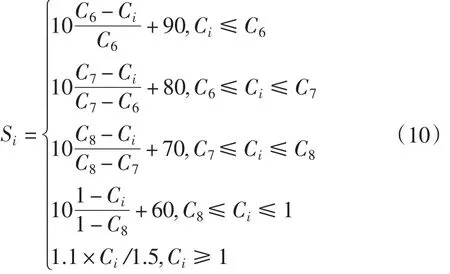
（7）利用文献[10]中单指标评分思想，可使用公式（10）对由上面计算得到的贴近系数进行计算，从而得到定量评分数据式中：Si代表的是评分函数，C6、C7、C8代表的是为判断各观测点电能质量状况的等级而设置的临界值，Ci代表的是待评估的样本的贴近系数。常规意义下，Ci不可以大于1，但本文扩展了其定义，使其可以在电能质量状况不合格的情况下出现大于1的情况，并使用了等级评分函数进行评估，这样可使得结果更为完整。

3 基于RSR法的排序和分档

秩和比法（Rank⁃sum ratio，RSR）是我国学者田凤调于1988年提出的，目前此法已日渐完善，广泛地应用于医疗卫生领域的多指标综合评价、统计预测预报、统计质量控制等方面[19—20]。在具体应用时，可先使用上述改进的TOPSIS法计算各贴近系数Ci,再借助RSR法对其进行排序分档，从而能更客观、全面、真实地分析评估问题。本文在此使用的目的是：利用常规的RSR法对上述评价结果进行排序分档，一方面可验证上文使用的分等级以评分函数给出的评价结果的准确性；另一方面欲借助RSR法进一步扩展，希望能够客观、全面、真实地反映各观测点的电能质量状况，从而使上述改进的TOPSIS法的应用更为合理。

下面将具体介绍其分析的步骤。

（1）对所得的8个贴近系数进行编秩。编秩原则：因为贴近系数是低优指标，故对其最大值编以1，次大值编以2，再依次类推到最小值编以n。

（2）计算RSR值，其计算公式如下

式中：m为指标数（本文由于只考虑贴近系数，故其设为1），n为样本数（本文对应为8），R为步骤（1）中编秩的秩次。

（3）确定RSR分布，将其按照从小到大排列起来，分别计算各RSR对应的频数f，向下累积频数f↓，秩次范围R，平均秩次和向下累计频率，再查《百分数与概率单位对照表》，求其所对应的概率单位值Y（百分数）。

（4）求出相应的回归方程RSR=a·Y+b；必要时对RSR还可选用适当代换量，以达到偏态对称化的目的。

（5）根据常用分档，计算分档的各个临界值，从而确定各个样本所在的分档情况。

4 实例应用

4.1 评估前数据预处理

本文以文献[13]中的实例数据为基础进行综合评估，其实测得到的某地某时段380 kV母线的电能质量相关数据如表2所示。

为便于有效排序和分级，本文引入了5种电能质量指标序列作为参考，其构造情况如表3所示。

在得到上述数据后，可以依此进行权重分析。再按照上述计算步骤可求得综合权重WW1，见表4。比例因子由文献[13]计算得α=0.316，β=0.684。

4.2 综合评估

4.2.1 快速定性评估

若只需了解各观测点大致的电能质量状况，可只需利用改进的TOPSIS法计算出各贴近系数Ci，并依此按从小到大进行排序，便可快速定性评估，这也是本方法区别于其他评估方法一个显著优点。以上述数据为例，只需一步计算，即可得知各观测点电能质量状况的优劣顺序为：1≥3≥4≥5≥2。

表2 观测点的电能质量测试数据

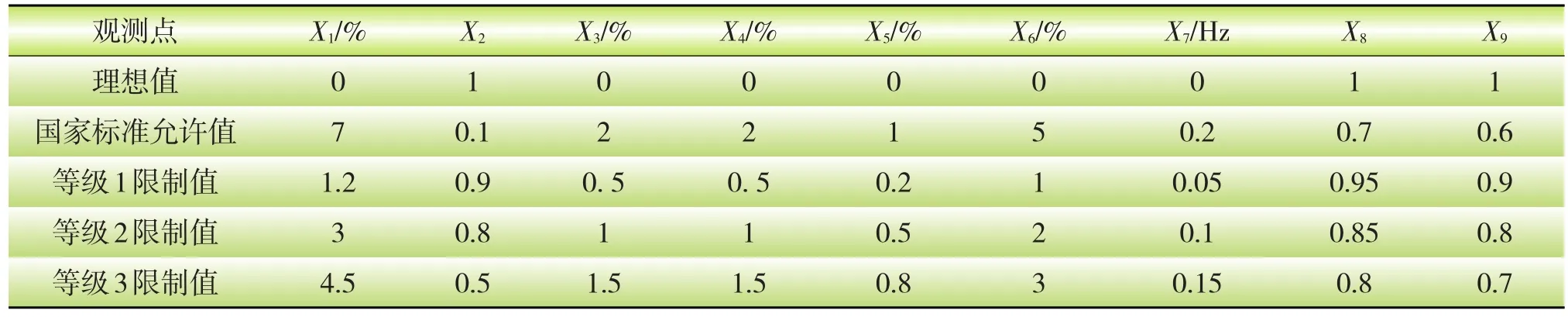
表3 用于参考的电能质量测试数据

4.2.2 定量评估

若要进一步定量评估，可按上述介绍的步骤进行分析，得到的评价结果如表5所示。

为了验证本方法的准确性，本文还应用了文献[3,6,13]的方法，对评估结果进行对比分析，结果见表6。

由表6可知，本文与文献[6,13]的结果一致，与文献[3]的结果相比，除观测点4以外，其他观测点评估等级均一致。观测点4中电压暂降X2及电压波动X4落在Q3之内，其余指标均位于Q4之内；同时，结合权重可知，取观测点4的电能质量为Ⅳ级更为合理些。其他观测点中，观测点1稍好于等级Ⅱ；观测点2、4、5虽处于等级Ⅳ范围内，但观测点4、5评估结果较观测点2明显更接近于等级Ⅲ，且观测点4较好于观测点5，结合客观数据分析可知，评估结果符合实际情况，具有可行性。

4.3 分级评估

在含有多层次的电能质量指标评估中，利用本文的评估方法，无需重新进行主客观权重的计算，只需保持某些条件不变的情况下，直接以总的贴近系数的形式，进行等级的判断，进而得出某层次某组指标的相对电能质量水平。

以观测点1为例做具体分析。在综合权重及理想值、国家标准允许值和等级限制值不变的情况下，将某层指标做如下分解：将每一个评估指标序列分为2组，该层指标中电压质量指标分为第1组，该层其余指标分为第2组，具体结果见表7。

由表7可知，观测点1中某层第1组指标的评估结果为Ⅱ级，结合评估分数，其稍高于80分，接近良好状态边界；而该层第2组指标评估结果为Ⅱ级，再结合评估分数，其高于80分，虽也靠近良好状态边界，但相比第一组要好些；同时，观测点1的电能质量综合评估等级为Ⅱ级，综合评分为介于两者之间，由此可得出：观测点1中某层的第2组指标的电能质量情况好于该层中的第1组指标，从而将观测点1的整体电能质量水平抬升。

表4 电能质量各评估指标权重

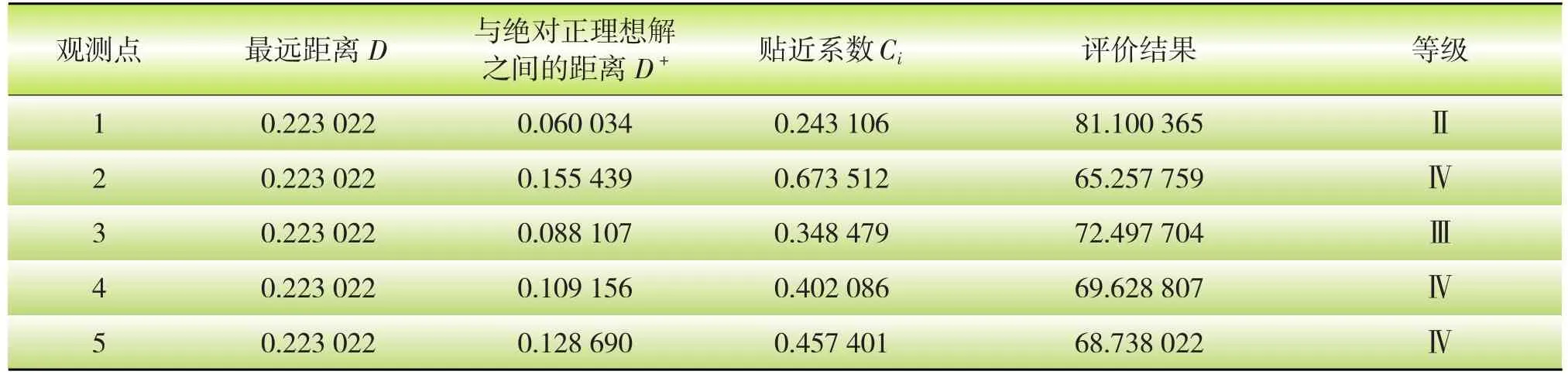
表5 电能质量评估结果

表6 电能质量评估结果对比

表7 观测点1实例分析

4.4 RSR法分档

依据上述介绍的有关RSR排序分档步骤，根据Ci值大小分组并进行相应分析，得到如表8所示结果。

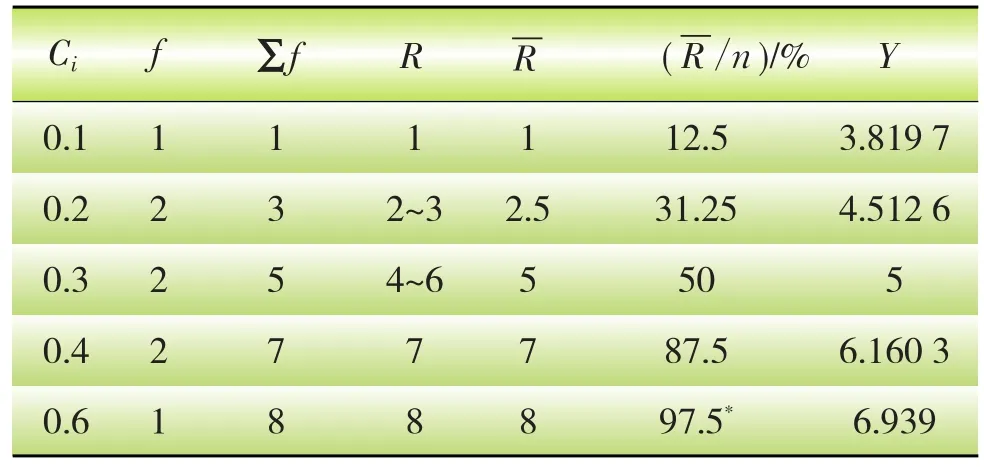
表8 Ci值分布及对应的概率单位值

应用最小二乘法求得贴近系数Ci与其对应的概率单位Y的线性回归方程Ci=0.151 1×Y-0.478 4，其相关系数r为0.985 5，回归效果的显著性检验F检验值是101.125 4，验证得该方程有效。据此利用RSR法进行合理分档，结果如表9所示。

表9 各观测点RSR评价的排序和分档

除观测点4外，其余分档结果与上述分级结果一致。4点之所以落在“中”上是因为RSR分档是以其常用分档概率等级进行，而非以上述预先设定好的固定等级（即此处的观测点6,7,8点）进行分档（即上面的分级），故有可能造成部分点落入其他区间的情况，这时候就只能通过观测其排序情况，与相应等级观测点相比，得出结论。本文观测点4就属于这样的情况，故此时只能通过等级观测点8来判断，其应该是落入合格区间，而非中区间，这样就与上面结论完全一致，验证了上述结论的正确性。

5 结束语

本文是将改进的层次分析法与主成分分析法相结合，根据线性赋权原理计算得到组合权重系数，以此为依据利用改进的TOPSIS法，结合单指标评分思想，对各项样本进行分等级打分的综合评估，取得了较为满意的结果。此外，本文还对某一层次下的某组电能质量指标进行分级评估。依此，可得到评估样本更为具体的电能质量水平，从而能有针对性地提出改进措施，避免因改善某一电能质量问题而恶化电网其他的电能质量指标。

为了验证该分等级综合评估方法的正确性，本文还使用了RSR法对由改进的TOPSIS计算得来的贴近系数进行进一步的排序分档处理，通过实例证明，该方法简单、实用，可迅速对各观测点电能质量情况进行定性和定量评估。

：

[1]徐永海,肖湘宁.电力市场环境下的电能质量问题[J].电网技术,2004,28(22)：48-52．

[2]江辉,彭建春,欧亚平,等.基于概率统计和矢量代数的电能质量归一量化与评价[J].湖南大学学报,2003,30(1)：66-70．

[3]唐会智,彭建春.基于模糊理论的电能质量综合量化指标研究[J].电网技术,2003,27(12)：85-88.

[4]黄剑,周林,栗秋华,等.基于物元分析理论的电能质量综合评估[J].重庆大学学报：自然科学版,2007,30(6)：66-70．

[5]刘颖英,李国栋,顾强,等.基于径向基函数神经网络的电能质量综合评价[J].电气应用,2007,26(1)：45-48.

[6]赵霞,赵成勇,贾秀芳,等.基于可变权重的电能质量模糊综合评价[J].电网技术,2005,29(6)：11-16.

[7]李娜娜,何正友.组合赋权法在电能质量综合评估中的应用[J].电力系统保护与控制,2009,37(16)：128-134.

[8]王增平,王雪.基于改进主成分分析的变压器励磁涌流识别方法[J].电力系统保护与控制,2011,39(12)：1-5,51．

[9]盛立东.模式识别导论[M].北京：北京邮电大学出版社,2010．

[10]雷刚,顾伟,袁晓冬.灰色理论在电能质量综合评估中的应用[J].电力自动化设备,2009,29(11)：62-65,70.

[11]熊以旺,程浩忠,王海群,等.基于改进AHP和概率统计的电能质量综合评估[J].电力系统保护与控制,2009,37(13)：48-52,71．

[12]康世崴,彭建春,何禹清.模糊层次分析与多目标决策相结合的电能质量综合评估[J].电网技术,2009,33(19)：113-118.

[13]李如琦,苏浩益.基于可拓云理论的电能质量综合评估模型[J].电力系统自动化,2012,36(1)：66-70.

[14]何古彪.变电站光伏发电系统的电能质量研究[D].上海：上海交通大学,2012．

[15]肖媛媛.应用TOPSIS法对门诊病人满意度进行综合评价[D].成都：四川大学,2007.

[16]Tavana,Madjid,Hatami⁃Marbini,et al.A group AHP ⁃TOPSIS framework for human spaceflight mission planning at NASA[J].Expert Systems with Applications,2011,38(11)：13 588-13 603.

[17]Xing Lixian,Tu Keran，Ma Ling,et al.The performance evaluation of IT project risk based on TOPSIS[C]//Proceedings⁃2009 International Conference on Computational Intelligence and Software Engineering，CiSE 2009：1-5．

[18]Rabiner L R,Rosenberg A E,Levinson S E.Fuzzy TOPSIS for group decision making：A case study for accidents with oil spill in the sea[J].Expert Systems with Applications,2011,38(4)：4 190-4 197．

[19]覃丹丹.应用TOPSIS法与RSR法评价医院的综合医疗质量[J].右江民族医学院学报,2005(5)：607-609.

[20]田凤调.秩和比法及其应用[M].北京：中国统计出版社,2002.

Synthetic evaluation of power quality based on improved TOPSIS and RSR method

YANG Zhi⁃xin1,YUAN Xiao⁃dong1,BAI Jing⁃jing2
（1.Jiangsu Electric Power Research Institute,Nanjing 210000,China;2.Southeast University,Nanjing 210096,China）

The quantized result from synthetic evaluation of power quality is one of the foundations to assess power quality and is favorable to implement the market mechanism of pricing electric ener⁃gy according to power quality.This paper uses the improved AHP and the principal component analysis(PCA)to determine the index of the combination weights;meanwhile,the improved TOPSIS and rank sum ratio(RSR)method is applied to the comprehensive assessment of the power quality,so the observation point of the power quality and the ideal value,standard value and rank values set up can be sorted and classified together,and power quality comprehensive evaluation can be achieved quickly.Calculation results of case study show that the proposed synthetical evaluation method is effective and feasible.

power quality;synthetic evaluation;PCA;im⁃proved TOPSIS;RSR

TM712

A

1009-1831（2013）05-0011-06

2013-03-06

国家电网公司2012年度重点科技项目《电能质量高级分析关键技术研究及应用》基金支持

杨志新（1968），男，江苏溧阳人，博士，高级工程师，主要研究方向为电力系统运行与控制、电网电能质量分析控制；袁晓冬（1979），男，江苏无锡人，专业主管，从事电能质量测试、仿真和测评工作；柏晶晶（1991），男，江苏大丰人，硕士研究生，主要研究方向为电网电能质量分析控制。