解决相似变换的两种新方法及联系
浙江省瑞安市塘下中学 叶挺彪 (邮编:325204)
提出好的问题,并巧妙地给予解决,由此形成一种新方法,这是“竞赛数学”发展的内在动力,对于与同向相似的两个图形有关问题,采用不同观点(变换观点、运动观点)导致两种新的处理方法.即“不动点法”[1]与“相对运动法”[2],并由此阐明其有机联系.
1 不动点法
对于同一平面上的两个同向相似形(不能通过平移使之重合),则在这平面上存在唯一的不动点M,使以M为中心将一个图形通过旋转、位似,就能与另一图形重合.由于点M沟通了两个图形的联系,在解题中若注意到这个点,可使问题迎刃而解.
利用不动点解题需知不动点的作法(见文[3]):即对不能通过平移使之重合的两个同向相似形F、F′,任取两条对应线段AB⊆F,A′B′⊆F′,则 四 条 直 线AB、A′B′、AB′、A′B交成的三角形(最多有四个)中,任两个三角形的外接圆的另一交点就是不动点M(称为不动点的共圆性).
例1 在△ABC两边所在的射线AC、BC上用尺规分别作出两点P、Q,满足PA=λQB(λ为给定的常数),并使PQ长最短.
分析 由于PA=λQB,可以把线段PA、QB看作相似比为λ∶1的两个相似形,于是考虑其不动点M与任意一对对应点构成的三角形中,寻找最小的三角形,即可获解.
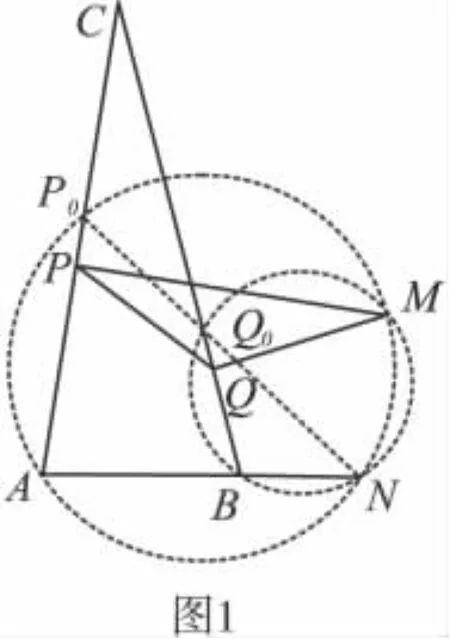
作法 (1)在射线AB、BC上分别取两点P0、Q0,使P0A=λQ0B.(如图1)
(2)作AP0与BQ0的不动点M.若P0Q0∥AB,则点C即为M,此时P、Q重合于C;若P0Q0交AB于N,则△NAP0与△NBQ0的外接圆的另一交点即为M.
(3)作MP⊥AC于P,MQ⊥BC于Q.
则P、Q为所求的点.
证明 由M为不动点知:
△MAP0∽ △MBQ0,而MP、MQ是它们对应边上的高.
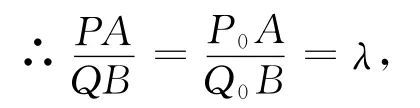
及△MPQ∽△MAB,再由MP为垂线段知:
线段PQ长最短.
说明 这里把具有相同分比的点所在线段看成是相似形,又如分别有一条对应半径的两个圆周也是相似形的特例.这些特例应引起重视.
从该例我们得出一般的结论.
结论 不能通过平移使之重合的两个同向相似形,它们的对应直线上所有点间的距离是以不动点在其上的射影点间距离为最短.
2 相对运动法
同向相似形上的两条对应线段所在直线上的对应点,它是两条线段上分比相同的分点,所以可以看作是作匀速运动的两动点在同一时刻的对应位置.所以对于相似形有关的问题可以用相对运动轨迹[2]加以巧妙解决.
所谓相对运动轨迹即作匀速直线运动(或同向匀速圆周运动)的两动点P、Q,将动线段PQ平移(旋转)使P与定点P0重合时,其线段为P0Q′,则Q′的轨迹是直线(圆周),Q′的轨迹我们称为相对运动轨迹.(见拙文[2])
例1另解:
分析 由于PA=λQB,则可将P、Q分别看作以速度比为λ∶1作匀速直线运动的两动点在某一时刻的对应位

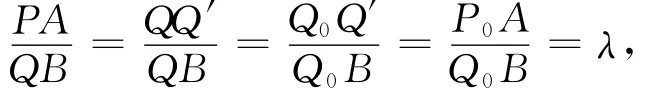
又对于满足PA=λQB的任意线段PQ,平移后的线段AQ′端点Q′的轨迹是BQ′,故由AQ′垂线段知:PQ长为最短.
说明 1°此处利用相对运动的轨迹BQ′,在其上找到满足条件的线段AQ′,最后将它反演到原问题的解PQ,轨迹BQ0′在这里起到桥梁的作用.
2°由结论:P、Q是不动点在两射线AC、BC上的射影.即分别作与AC、BC垂直的直线,这两直线交点即为不动点M,如图2,从而得不动点的新作法.此处从略.
下面再介绍第三种作法:
3 两者的联系——不动点的新作法
例2 设不能通过平移使之重合的的两个同向相似形F、F′,试作出F、F′的不动点M.
分析 将F、F′上所有对应点确定的线段PQ平移到AQ′,在此变换下,若动点Q′形成图形F″,则F及F′的象成为点A及图形F″.
若将点看作与任意图形相似,则后者的不动点显然是A.
于是将F″反演到F′时,A在F″中就被反演到原两相似形F、F′的不动点M.
作法 (1)在F、F′上分别取两条对应线段:AP0⊆F、BQ0⊆F′(如图2).
(2)作 ▱AP0Q0Q0′.
(3)作 △BQ0M∽ △BQ0′A且旋向相同.置,为此,作出相对运动轨迹,从其上寻找问题的解,最后反演到原问题的解.
作法 (1)在射线AC、BC上分别取P0、Q0使P0A=λQ0B(如图2).
(2)作 ▱AP0Q0Q0′,得相对运动轨迹BQ′.
(3)作AQ′⊥BQ0′于Q′.
(4)作Q′Q∥AC交BC于Q,作QP∥AQ′交AC于P.
则P、Q为所求的点.
证明 由作法知:
则M为所求的点.
证明 设从F到F′相似变换为[3]:
f(z)=az+b(这里a、c∈C为常数,z为复变量),则

(这里仍用大写字母表示该点的复数)

又∵△BQ0M∽△BQ0′A且旋向相同,

将①、②代入上式整理得:
M=aM+b,即f(M)=M,
∴M是两相似形F、F′的不动点.
例3 在四边形ABCD中,AB=CD,EF为AD、BC的中点(如图3),延长EF分别交BA、CD的延长线于G、H,求证:∠BGF=∠CHF.

分析1 由于E、F分别是AD、BC的中点,把A、E、D与B、F、C分别看作两动点A、B在三个不同时刻的对应位置,为此作出B相对于A的运动轨迹,即分别把线段EF、DC平移到AF′、AC′,由结论1,知B、F′、C′三点共线.

∴∠1=∠2,从而∠BGF=∠CHF.
说明 从分析过程不难发现上述命题可作如下推广:
2°沿任何方向作直线运动,相对运动轨迹仍是直线,所以可以把凸四边形换成凹四边形或折四边形,结论也同样成立.
分析2 如图4,由点E、F分别是BC、AD的中点,知AFD∽BEC.这启发我们作出它们的不动点M,即△HFD与△HEC的外接圆的另一交点.则△MAB∽△MDC.
又AB=DC,
∴△MAB≌△MDC,
∴MB=MC,
因此△MBC是等腰三角形.
由不动点的共圆性知:
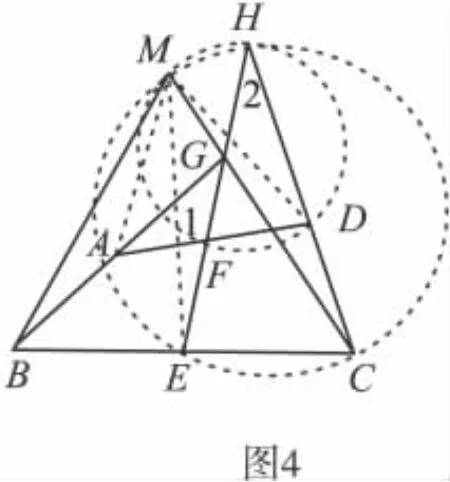

∠1=∠BME,
∠2=∠CME,
而∠BME=∠CME,
∴∠1=∠2.
说明 1°也可以作△BCM∽△BC′A且同向则M为不动点如图5.
2°分比相同的分点与线段所成的图形是同向相似的特例.注意到这种特例,可应用不动点解题.
一般地,对于与相似形F、F′有关的问题,有两种新的途径:相对运动法,不动点法,从这些例可见一斑.这两种转化在竞赛中有其广泛的应用,限于篇幅,不再累述.
1 叶挺彪.不动点在平几证题中的应用[J].福建中学数学,1996(3).
2 叶挺彪.相对运动的几何模型及应用[J].中学数学杂志,1995(5)
3 叶挺彪.相似变换下的不动点作法及应用[J].中等数学,1993(3)

